钢筋混凝土抗震框架连续倒塌行为分析

黄华+刘伯权+张彬彬+吴涛

摘要：以某抗震设防框架为研究对象，采用SAP2000有限元软件，依次拆除底层纵向边柱、横向边柱、角柱和内柱，研究抗震框架的倒塌破坏行为。以做功平衡原理建立了柱失效处梁配筋调整计算公式，并进行了配筋调整设计。结果表明：7度和8度抗震设防的框架结构仍会发生连续性倒塌，但是抗倒塌能力随着设防等级的提高而提高，抗震设计不能够完全替代抗倒塌设计；柱失效导致结构发生连续坍塌破坏的危险性由小到大依次为内柱、横向边柱、纵向边柱、角柱；梁铰机制在结构抗倒塌中的作用尤其重要，倒塌破坏时以梁的弯曲破坏为主，剪切破坏较少出现；线弹性静力分析计算的供需比最大值一般出现在失效柱上一层的相邻梁上，而非线性静力分析的最大破坏出现在与失效柱相连的梁上，但是二者对结构可能的失效位置判断基本一致。

关键词：结构工程；抗震框架；连续倒塌；抽柱；有限元分析

中图分类号：TU375.4 文献标志码：A

0 引 言

工程结构服役期间可能会遭受诸如煤气爆炸、恐怖袭击、火灾、撞击等偶然荷载，导致结构局部破坏或损伤，从而造成严重的人员伤亡和财产损失。自1968年英国Ronan Point公寓因煤气爆炸造成连续倒塌后，国外开展了较为广泛的结构抗连续倒塌性能研究。经历美国1995年Alfred P. Murrah联邦政府办公楼和2001年纽约世贸大厦等多起重大连续性倒塌事件后，建筑结构连续倒塌问题受到了工程界的广泛关注，已成为21世纪以来土木工程学科的研究热点[1-2]。中国虽然在《混凝土结构设计规范》（GB 50010—2010）和《高层建筑混凝土结构技术规程》（JGJ 3—2010）中给出了抗连续倒塌设计的基本原则和计算方法，但是当前仍缺少针对连续倒塌设计的专门规范，并且中国现役建筑中进行过抗连续倒塌设计的屈指可数，仅在个别大型重要建筑中进行了连续倒塌分析[3]，如国家体育场、广州新电视塔、新广州火车站、上海虹桥综合交通枢纽工程等。2001年3月河北石家庄特大连环爆炸案和2003年湖南衡阳大厦特大火灾倒塌事件等已足够说明中国现役建筑在抗连续倒塌能力方面存在不足。

虽然众多研究者[4-8]认为抗震结构的冗余特性和延性能力等要求对提高结构的抗连续倒塌能力是有益的，抗震结构具有较好的抗连续倒塌能力，但是结构的抗连续倒塌设计与抗震设计二者之间存在显著差别，抗震设计方法虽然有益于结构的抗连续倒塌能力，却不足以让它取代抗连续倒塌设计[9-11]。当前的研究在一定程度上认可抗震设计对抗连续倒塌的积极作用，但是对其具体的力学行为和倒塌设计方法仍缺乏足够的分析。本文借助SAP2000有限元软件，以某抗震框架为研究对象，分析其连续倒塌行为，并提出了抗倒塌设计方法，为连续性倒塌设计提供了参考。

1 模型的建立

结构分析以某4层框架为例展开，模型柱网尺寸如图1所示。梁柱编号以横轴线、纵轴线和层数表示，如B1-12A为第1层①，②轴线之间，位于轴线上的梁，C1-1A为第1层①轴线和轴线相交处的柱。以此类推得到第2层②，③轴线之间，位于轴线上的梁为B2-23A。结构中，轴线之间的梁截面尺寸为250 mm×250 mm，其余均为250 mm×500 mm；柱截面尺寸全部为400 mm×400 mm；楼板及屋面板厚度均为120 mm。混凝土强度等级为C30，纵筋为HRB335，箍筋及板配筋均为HPB300。

结构抗震设防烈度为7度0.1g（g为重力加速度），设计地震分组为第1组，二类场地，抗震等级三级。楼面活载标准值为2.0 kPa，将面层和顶棚等折算后的楼面恒载为3.7 kPa；不上人屋面的活载标准值为0.7 kPa，恒载为4.9 kPa。建筑所在地的基本风压和基本雪压分别为0.40，0.65 kPa。

采用PKPM计算得到结构内力和配筋，将其模型导入SAP2000后，以备用荷载路径法，通过拆除关键构件分析抗震框架的连续倒塌性能。由于结构简单，层数少，各层杆件配筋相差不大，考虑钢筋归并以及分析简便，各层梁柱配筋与底层相同。倒塌荷载采用等效静力法，根据美国GSA 2003[12]规范进行取值，具体如下：

（1）直接承受倒塌荷载的构件

仅拆除首层竖向关键构件时

静力分析

式中：DS为关键构件失效时结构构件或节点所受到的弯矩、剪力或轴力等；D0为结构构件或节点所能承受的弯矩、剪力或轴力等。

计算式（6）时考虑快速加载的材料强度提高系数取1.25。

美国GSA 2003规范认为：规则结构Dcr>2.0，不规则结构Dcr>1.5时，结构连续倒塌的概率较高。以下分析认为结构的Dcr满足此条件即发生倒塌。

非线性静力分析时，以延性和转角大小来表示结构破坏，非线性分析评估标准如表1所示。

在以上原则基础上，本文对钢筋混凝土框架结

构底层柱失效后的构件破坏、内力重分布等进行分析，研究结构的连续倒塌行为。2 结构连续倒塌行为

根据美国GSA 2003规范，以本文框架结构作为规则结构，构件失效可能为：结构纵轴向某根边柱失效；结构转角处的某根角柱失效；结构横轴向某根边柱失效；结构内部的某根柱失效。因此，按此原则逐次拆除底层关键柱，分析其失效后结构的倒塌行为。

2.1 拆除底层纵向边柱C1-3A

拆除底层纵向边柱C1-3A，通过线弹性静力分析和非线性静力分析，分别讨论结构可能出现的倒塌行为。

2.1.1 线弹性静力分析

底层纵向边柱C1-3A失效后，轴线和③轴线的弯矩和剪力见图2。由图2可知，纵向边柱失效后，与之相连的构件内力变化较大，而对相邻框架的影响有限，其中，纵轴向形成的双跨梁两端以及横轴向形成的悬臂梁固定端负弯矩和剪力均增大，且随楼层增高，各层梁的弯矩和剪力逐渐减小。双跨梁的跨中弯矩由负变为正，剪力则由正变为负，且弯矩和剪力最大值出现在结构第2层，并分别向上层和下层减小。悬臂梁的自由端弯矩由负变为正，但是剪力没有改变方向，且除了底层外其余剪力均减小。endprint

根据式（6）计算出的各杆件供需比Dcr值见图3，其中梁上部数值为弯矩的Dcr值，梁下部数值为剪力的值。根据图3中的Dcr分布可知，失效柱上方的纵轴向梁除顶层双跨梁两端外，弯矩的Dcr值均大于2.0，且双跨梁两端的Dcr值随层数增高而减小，但是跨中Dcr值最大出现在结构第2层，达到3.78，然后随层数增加而减小，顶层亦达到3.35，可认为其达到失效状态。横轴向框架梁形成悬臂梁，Dcr值分布规律与纵轴向相同，但是由于该方向中间跨度较小，两柱间距近，内力重分布效果好于纵轴向，弯矩的Dcr值小于2.0。同时，轴线和①轴线这2个轴线方向剪力的Dcr值均小于2.0，梁主要是发生弯曲破坏。

2.1.2 非线性静力分析

在线弹性分析基础上，采用竖向Push-over分析柱C1-3A失效后的结构受力性能。梁柱弯矩-转角曲线见图4，其中A点为原点，随荷载增加，塑性铰

达到屈服点B，在AB之间铰处于刚性阶段；随着荷载继续增加，塑性铰分别达到IO，LS，CP三个阶段，分别对应直接使用、生命安全和防止倒塌阶段；然后达到极限承载力点C，随后承载力降至残余强度点D，最终到达完全失效点E。倒塌分析时，施加荷载后通过杆件各塑性铰达到的变形量来查看其性能，并判断结构是否满足期望的能力目标。

框架轴线和③轴线上塑性铰出现顺序如图5所示。由图5（a）可知，随荷载增加，纵向框架梁塑性铰屈服首先发生在底层双跨梁两端，之后逐步向上层发展，并随荷载增加，塑性铰在如图4所示的曲线上向C点发展。底层双跨梁两端最先达到CP阶段，且双跨梁跨中塑性铰发展始终落后于梁两端，并随层数增大，塑性铰的发展逐步减缓。最终底层双跨梁两端承载力达到D点，说明结构发生彻底破坏。以上各层塑性铰基本保持在LS阶段，但是由塑性铰发育程度可知，结构第2层基本接近CP阶段。由图5（b）可知，随荷载增加，横轴向悬臂梁塑性铰屈服首先发生在固定端，并逐渐向上层发展，塑性铰出现规律与纵轴向一致，但是横轴向塑性铰最终均未达到CP阶段，而是停留在LS阶段。

结合线弹性静力分析结果可知，纵轴向框架破坏较横轴向严重，结构最终发生破坏的范围基本限制在底下2层，上部结构存在损伤，但是并不严重，临近框架基本没有进入屈服阶段，底层纵向边柱缺失对结构影响有限。与线弹性静力分析进行比较可知，二者计算结果存在一定差异，但是在可能的失效位置判断上基本一致，线弹性静力分析结果不能简单根据供需比Dcr大小判断其破坏严重程度。

2.2 拆除底层横向边柱C1-1B

拆除底层横向边柱C1-1B，鉴于篇幅有限，仅通过线弹性静力分析来讨论底层横向边柱失效后结构可能出现的倒塌行为。计算得到柱C1-1B失效后轴线和①轴线的弯矩、剪力见图6。

由图6可知，横向边柱失效后，与之相连的构件失效后的内力

Fig.6 Internal Forces After Column C1-1B Failure内力变化较大，而对相邻框架的影响有限。纵轴向框架悬臂梁固定端负弯矩和剪力均增大，且随层数增加而减小；自由端弯矩由负变为正，剪力保持原来方向，但是除底层外弯矩和剪力均减小。横轴向双跨梁两端负弯矩和剪力均增大，且随楼层增高而逐渐减小；跨中负弯矩变为正弯矩，弯矩最大值出现在结构第2层，且短跨一侧要远大于长跨一侧；跨中短跨一侧剪力改变方向并增大，除长跨底层剪力外其余的剪力最大值均出现在结构第2层，并分别向上层和下层减小。

根据式（6）计算出的各杆件供需比Dcr值见图7。根据图7中的Dcr分布可知，失效柱上方的纵轴向梁弯矩的Dcr值均小于2.0，且随层数增大而减小。横轴向框架梁所形成的双跨梁两端的Dcr值随层数增高而减小，但是跨中Dcr值最大出现在结构第2层，然后随层数增加而减小，其中梁B1-1BC右端和梁B2-1BC左端的Dcr值大于2.0，可认为结构达到失效状态，这与其相对刚度大，柱失效后分担的荷载较大有关。所有剪力的Dcr值均小于2.0，梁主要是发生弯曲破坏。与拆除底层纵向边柱相比，构件失效的数量和范围要小得多。

图7 柱C1-1B失效后的Dcr分布

Fig.7 Distributions of Dcr After Column C1-1B Failure2.3 拆除底层角柱C1-1A

拆除底层角柱C1-1A，通过线弹性静力分析来讨论底层角柱失效后结构可能出现的倒塌行为。计算得到柱C1-1A失效后轴线和①轴线的弯矩、剪力如图8所示。

由图8可知：底层角柱C1-1A失效后，同样与之相连的构件内力变化较大，而对相邻框架的影响有限，其中，纵轴向框架悬臂梁固定端负弯矩和剪力均增大，且随层数增加而减小；自由端弯矩和剪力均由负变为正，弯矩和剪力最大值出现在结构第2层，并分别向上层和向下层减小。横轴向框架悬臂梁固定端弯矩和剪力均增大，且随楼层增高而逐渐减小；自由端负弯矩变为正弯矩，而剪力虽保持方向不变但是剪力减小，弯矩最大值出现在结构第2层，并且向上层减小。

根据式（6）计算出的各杆件供需比Dcr值见图9。根据图9中的Dcr分布可知，纵轴向悬臂梁除顶层固定端外弯矩的Dcr值均大于2.0，弯矩的Dcr值最大出现在结构第2层自由端，达到3.13。横轴向弯矩的Dcr值大于2.0出现在第1～3层的固定端，底层最大，为2.7。因此破坏最严重的基本上在第1，2层，并最终可能导致角部所有楼层坍塌。所有剪力的Dcr值均小于2.0，梁主要是发生弯曲破坏。拆除底层角柱时，构件失效的数量和范围相对最大，角柱失效造成的双向悬臂梁型倒塌机制对结构抗的倒塌承载力最为不利。

2.4 拆除底层内柱C1-3B

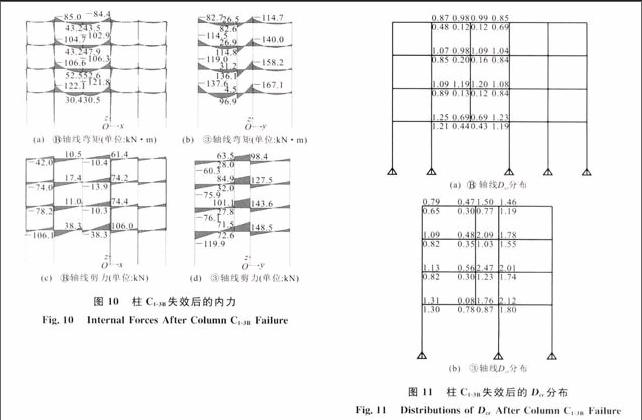
拆除底层内柱C1-3B，通过线弹性静力分析来讨论底层内柱失效后结构可能出现的倒塌行为。通过计算可得到底层内柱C1-3B失效后轴线和③轴线的弯矩、剪力如图10所示。endprint

由图10可知，底层内柱失效后，同样与之相连的构件内力变化较大，而对相邻框架的影响有限。纵轴向和横轴向分别形成的双跨梁两端负弯矩和剪力均增大，且随楼层增高，各层梁的弯矩和剪力逐渐减小。纵轴向双跨梁的跨中弯矩由负变为正，且弯矩最大值出现在结构第2层，并分别向上层和下层减小；剪力保持方向不变，但是数值上大幅减小，剪力最大值出现在底层。横轴向双跨梁跨中弯矩由负变为正，弯矩最大值出现在结构第2层，且短跨一侧要远大于长跨一侧；跨中短跨一侧剪力改变符号且增大，除长跨底层剪力外其余剪力最大值均出现在结构第2层，并分别向上层和下层减小。

根据式（6）计算出的各杆件供需比Dcr值见图11。根据图11中的Dcr分布可知，失效柱上方的纵轴向双跨梁弯矩Dcr值均小于2.0，且双跨梁两端的Dcr值随层数增高而减小，但是跨中Dcr值最大出现在结构第2层。横轴向双跨梁Dcr值分布规律与纵轴向相同，但是由于该方向中间跨度较小，短跨一侧梁由于刚度相对较大，所承担的荷载也大，梁B1-3BC右端、梁B2-3BC左端和右端、梁B3-3BC左端弯矩的Dcr值均大于2.0，且梁B2-3BC左端最大，达到2.47，可认为结构失效。同时，图11中的轴线和③轴线这2个轴线方向剪力的Dcr值均小于2.0，梁主要是发生弯曲破坏。底层内柱失效时，由于在纵向、横向均形成双跨梁，荷载重分布途径最多，因此结构破坏范围和程度相对较低。

3 设防等级对结构抗倒塌能力的影响

结构设防烈度改为8度0.2g，其他设计条件同上文，PKPM计算配筋后，将其模型导入SAP2000，同样拆除底层纵向边柱C1-3A，通过线弹性静力分析，讨论结构可能出现的倒塌行为。

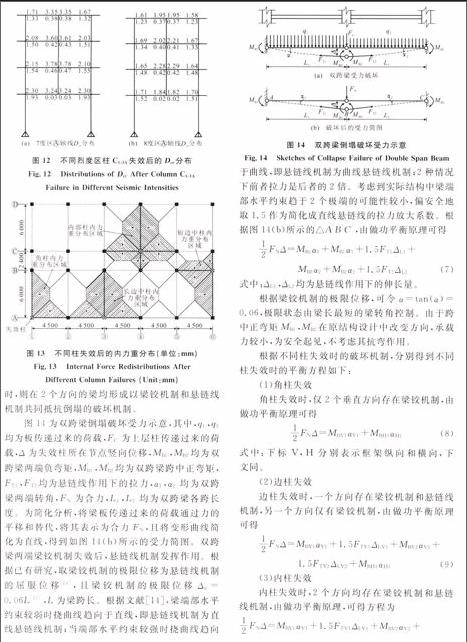
计算得到柱C1-3A失效后，轴线各杆件的供需比Dcr与第2节中设防烈度为7度0.1g的计算结果对比见图12。由图12可知，二者Dcr值分布规律基本相同，但是抗震设防烈度提高后，结构的抗倒塌能力有了显著提高，8度区结构仅在第2，3层双跨梁跨中供需比超限，且超限幅度并不大。结构设防烈度的提高，使得结构配筋量增加，增强了与失效构件连接梁的拉结强度，并提高了结构荷载的重分布能力，从而提高结构的抗连续性倒塌能力。由于设防烈度提高会导致结构用钢量大幅增加[13]，从而造成建设成本不合理增长，因此并不能够简单地通过提高设防烈度来增强结构的抗倒塌能力。

4 连续倒塌设计方法

根据以上分析，框架柱失效后对其临近框架影响很小，可以认为内力重分布符合如图13所示的规则。不同柱失效后的破坏机制不同：对于角柱失效，2个方向的梁均处于悬臂状态，不能以悬链线机制提供有效的拉结力，因此只能以梁铰机制提供结构倒塌抗力；边柱失效时则在结构边缘方向形成以梁铰机制和悬链线机制共同抵抗倒塌的破坏机制，在垂直方向则以梁铰机制提供倒塌抗力；内部柱失效 时则在2个方向的梁均形成以梁铰机制和悬链线机制共同抵抗倒塌的破坏机制。

图14为双跨梁倒塌破坏受力示意，其中，q1，q2均为板传递过来的荷载，FC为上层柱传递过来的荷载，Δ为失效柱所在节点竖向位移，MB1，MB2均为双跨梁两端负弯矩，M′B1，M′B2均为双跨梁跨中正弯矩，FT1，FT2均为悬链线作用下的拉力，α1，α2均为双跨梁两端转角，FN为合力，L1，L2均为双跨梁各跨长度。为简化分析，将梁板传递过来的荷载通过力的平移和替代，将其表示为合力FN，且将变形曲线简化为直线，得到如图14（b）所示的受力简图。双跨梁两端梁铰机制失效后，悬链线机制发挥作用。根据已有研究，取梁铰机制的极限位移为悬链线机制的屈服位移[14]，且梁铰机制的极限位移Δu=0.06L[15]，L为梁跨长。根据文献[14]，梁端部水平约束较弱时挠曲线趋向于直线，即悬链线机制为直线悬链线机制；当端部水平约束较强时挠曲线趋向

于曲线，即悬链线机制为曲线悬链线机制；2种情况下前者拉力是后者的2倍。考虑到实际结构中梁端部水平约束趋于2个极端的可能性较小，偏安全地取1.5作为简化成直线悬链线的拉力放大系数。根据图14（b）所示的△B′A′C′，由做功平衡原理，可得

根据梁铰机制的极限位移，可令α=tan（α）=0.06，极限状态由梁长最短的梁转角控制。由于跨中正弯矩M′B1，M′B2在原结构设计中改变方向，承载力较小，为安全起见，不考虑其抗弯作用。

根据不同柱失效时的破坏机制，分别得到不同柱失效时的平衡方程如下：

（1）角柱失效

角柱失效时，仅2个垂直方向存在梁铰机制，由做功平衡原理可得

根据以上关系，由PKPM计算得到的配筋反算弯矩，并优先设置通长钢筋，即在原配筋基础上增设通长钢筋，可较少增加配筋量。由式（8）～（10）计算的做功见表2，调整如图1所示结构7度设防时的底层设计配筋见图15，考虑板的薄膜效应以及材料设计值与标准值之间的安全储备，上述式（8）～（10）不再进行安全系数的调整。

由表2可知，梁铰机制在结构倒塌时耗散能量为悬链线机制的2倍左右，其在结构抗倒塌中的作用尤其重要。由图15可以看出，框架结构倒塌设计配筋调整关键在于角柱，与其相连的梁配筋量增加最大，其次是边柱，而内柱失效后配筋调整并不大。5 结 语

（1）7度和8度抗震设防的框架结构仍会发生连续性倒塌，但是抗倒塌能力随着设防等级提高而提高，抗震设计不能够完全替代抗倒塌设计。

（2）框架结构中，柱失效导致其连续坍塌的危险性由小到大依次为内柱、横向边柱、纵向边柱、角柱，梁铰机制在结构抗倒塌中的作用尤其重要，倒塌破坏时以梁的弯曲破坏为主，剪切破坏较少出现。

（3）线弹性静力分析和非线性静力分析的计算结果存在一定差异，但是对结构可能的失效位置判断基本一致。非线性静力分析最大破坏出现在与失效柱相连的梁上，而线弹性静力计算的最大供需比一般出现在失效柱上一层的相邻梁上，因此不能简单根据供需比大小判断其破坏严重程度。endprint

（4）在仿真分析基础上，以做功平衡原理建立了柱失效处梁配筋调整计算公式，并进行了配筋调整设计，钢筋增量最大的是与角柱相连的梁，其次是与边柱相连的梁，而与内柱相连的梁配筋增量不大。

参考文献：

References：

[1] CROWDER B，STEVENS D J，MARCHAND K A.Design of Buildings to Resist Progressive Collapse[C]//Virginia Society of Professional Engineers.Short Course Proceedings of Security Engineering Workshop.Charlottesville：Virginia Society of Professional Engineers，2004：1-14.

[2]MOHAMED O A.Progressive Collapse of Structures：Annotated Bibliography and Comparison of Codes and Standards[J].Journal of Performance of Constructed Facilities，2006，20（4）：418-425.

[3]单 亮，汪 洋.现代结构工程中的连续倒塌研究[J].工业建筑，2007，37（增）：615-623.

SHAN Liang，WANG Yang.The Study of Progressive Collapse in Modern Structural Engineering[J].Industrial Construction，2007，37（S）：615-623.

[4]BAO Y H，KUNNATH S K，EI-TAWIL S，et al.Macromodel-based Simulation of Progressive Collapse RC Frame Structures[J].Journal of Structural Engineering，2008，134（7）：1079-1091.

[5]CORLEY W G.Applicability of Seismic Design in Mitigating Progressive Collapse[C]//National Institute of Building Sciences.Proceedings of National Workshop on Prevention of Progressive Collapse.Washington DC：National Institute of Building Sciences，2002：10-11.

[6]HAYES J R，WOODSON S C，PEKELNICKY R G.Can Strengthening for Earthquake Improve Blast and Progressive Collapse Resistance？[J].Journal of Structural Engineering，2005，131（8）：1157-1177.

[7]BILOW D N，KAMARA M.U.S.General Services Administration Progressive Collapse Design Guidelines Applied to Concrete Moment-resisting Frame Buildings[C]//ASCE.Structures 2004：Building on the Past，Securing the Future.Reston：ASCE，2004：1-27.

[8]江晓峰，陈以一.建筑结构连续性倒塌及其控制设计的研究现状[J].土木工程学报，2008，41（6）：1-8.

JIANG Xiao-feng，CHEN Yi-yi.A Review on the Progressive Collapse and Control Design of Building Structures[J].China Civil Engineering Journal，2008，41（6）：1-8.

[9] OSTERAAS J D.Murrah Building Bombing Revisited：A Qualitative Assessment of Blast Damage and Collapse Patterns[J].Journal of Performance of Constructed Facilities，2006，20（4）：330-335.

[10] POWELL G.Progressive Collapse：Case Studies Using Nonlinear Analysis[C]//ASCE.Structures Congress 2005：Metropolis and Beyond.Reston：ASCE，2005：1-14.

[11] GURLEY C.Progressive Collapse and Earthquake Resistance[J].Practice Periodical on Structural Design and Construction，2008，13（1）：19-23.

[12]GSA 2003，Progressive Collapse Analysis and Design Guidelines for New Federal Office Buildings and Major Modernization Project[S].

[13]张彬彬.钢筋混凝土框架结构抗连续性倒塌的数值分析[D].西安：长安大学，2011.

ZHANG Bin-bin.The Numerical Analysis of Reinforced Concrete Frame Structure Resisted Progressive Collapsed Performance[D].Xian：Changan University，2011.

[14]李 易.RC框架结构抗连续倒塌设计方法研究[D].北京：清华大学，2011.

LI Yi.Study on Design Method for RC Frame Structures to Resist Progressive Collapse[D].Beijing：Tsinghua University，2011.

[15]徐福江.钢筋混凝土框架-核心筒结构基于位移抗震设计方法研究[D].北京：清华大学，2006.endprint