型钢混凝土组合框架力学性能非线性分析
2015-02-03王琨袁沈峰曹大富郑文忠
王琨+袁沈峰+曹大富+郑文忠

摘要:在充分考虑混凝土损伤、材料非线性及单元类型的基础上,建立了由预应力(非预应力)型钢混凝土梁及角钢混凝土柱构成的型钢混凝土组合框架有限元模型,对其在水平荷载作用下的力学性能进行数值分析及试验对比验证。在此基础上,进一步研究了水平荷载作用下组合框架受力的全过程,并对影响此类框架力学性能的主要因素进行了参数敏感性分析。结果表明:组合框架在梁端和柱底部均出现塑性铰,能实现“强柱弱梁”的破坏机制;随着轴压比增大,水平荷载-位移曲线峰值荷载先增加后减小,峰值荷载对应的位移减小,延性降低;随着长细比增加,结构刚度降低,峰值荷载减小,延性增加。
关键词:型钢混凝土梁;角钢混凝土柱;有限元;力学性能;峰值荷载
中图分类号:TU375.1 文献标志码:A
0 引 言
预应力型钢混凝土组合框架具有承载力高、抗震性能好及裂缝可控等优点,已在大跨、承重及转换结构中得到了广泛的研究与应用[1-3]。在此基础上,本文中结合套建增层改造实践经验,提出了一种以预应力型钢混凝土梁作为框架梁,以角钢混凝土柱作为框架柱的新型预应力型钢混凝土组合框架结构。由于该结构在施工阶段可通过梁内型钢承担施工荷载和流态混凝土自重,实现施工阶段自承重的功能,同时其预应力筋和喇叭管在框架节点内部布置相对容易,节点构造简单,已在哈尔滨南岗会堂增层改造工程中得到了应用[4]。
目前,笔者已针对此类组合框架结构开展了相关试验研究,并采用OpenEES从宏观层面对此类组合框架开展了滞回性能分析[5]。然而,宏观层面虽然能给出相关参数对组合框架抗震性能的影响规律,但是难以从组合结构破坏过程、破坏形态及局部微观应力、应变状态等层面进行深入研究。
为此,本文中拟依据试验结果基于ABAQUS平台建立组合框架精细化有限元模型,考察框架在水平荷载作用下的受力全过程,并对梁柱端混凝土、型钢及纵筋的微观应力、应变状态进行细致分析,探讨组合框架在水平荷载下的受力机理,并进一步研究不同参数对组合框架荷载-位移曲线的影响,其结果可为相关研究和工程设计提供参考。
1 数值模型的建立
1.1 基本假定
基本假定如下:①钢筋、型钢和预应力筋与混凝土之间完全粘结;②不考虑混凝土徐变、收缩的影响;③不考虑加载速率对材料强度的影响。
1.2 材料本构模型
(1)混凝土本构模型。混凝土本构采用损伤塑性模型[6],屈服条件由Lubliner等[7]提出,并由Lee和Fenves进行修正,同时采用塑性势面与屈服面不同的、不相关联的流动法则。塑性势面采用Drucker-Prager[8]提出的静水压力面。
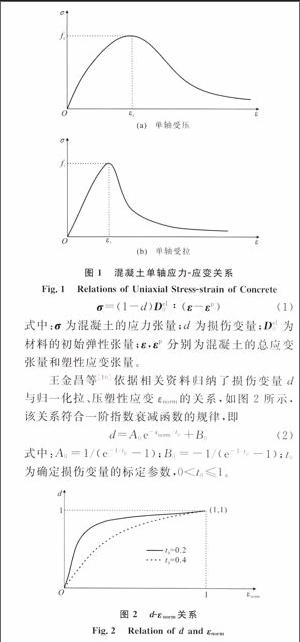
混凝土单轴应力-应变曲线采用《混凝土结构设计规范》(GB 50010—2010)[9]附录C推荐的本构关系,如图1所示,其中,ε为应变,σ为应力,fc为抗压强度,ft为抗拉强度,εc为压应变,εt为拉应变。混凝
式中:σ为混凝土的应力张量;d为损伤变量;Del0为材料的初始弹性张量;ε,εp分别为混凝土的总应变张量和塑性应变张量。
王金昌等[10]依据相关资料归纳了损伤变量d与归一化拉、压塑性应变εnorm的关系,如图2所示,该关系符合一阶指数衰减函数的规律,即
式中:A0=1/(e-1/t0-1);B0=-1/(e-1/t0-1);t0为确定损伤变量的标定参数,0 Fig.2 Relation of d and εnorm(2)钢材本构模型。工字型钢、角钢、钢板箍、纵筋和箍筋均采用理想弹塑性本构模型,其应力-应变关系如图3所示,其中,σs为钢材应力,εs为钢材应变,fy,f′y均为屈服强度,εy,ε′y均为屈服应变。 3)预应力筋本构模型。预应力筋应力-应变关系采用的三折线模型[11]见图4,其中,σp为预应力筋应力,εp为预应力筋应变,Ep1为比 例阶段弹性刚度,Ep2为非比例阶段弹性刚度,Ep3为条件屈服后的屈服刚度,fp1,fp2,fp3均为折点处的应力,εp1,εp2,εp3均为折点处的应变。 1.3 单元类型选择及模型建立 二次缩减积分单元不仅能够克服线性单元的自锁及线性缩减积分单元的沙漏问题,而且其与二次完全单元相比计算效率高、计算精度基本相同、对网格划分敏感性较小[12],因此本文中采用二次缩减积分单元中的实体单元C3D20R来模拟框架结构中的混凝土[13]。 钢梁的翼缘和腹板、角钢及钢板箍沿厚度方向的尺寸远小于其他方向,通常不考虑其沿厚度方向的应力分布,故常采用壳单元S4R来模拟。纵筋、箍筋和预应力筋则通过杆单元T3D3来模拟。 鉴于模型较为复杂,本文中对框架、钢梁、钢筋骨架、角钢骨架及预应力筋分别建模及划分单元,并用ABAQUS提供的Embed技术进行自由度耦合,以实现框架的整体建模。网格划分后的预应力型钢混凝组合框架(PSRCF)有限元模型见图5,非预应力框架(SRCF)模型与之类似,不再赘述。 1.4 施加约束及荷载 对框架柱柱底部截面施加固接约束,为避免应力集中,在柱顶面和梁顶面上共设置4个刚度较大的弹性垫板以承担竖向集中荷载,在梁端设置刚度较大的弹性垫板以承担水平荷载。预应力作用会对梁两端产生集中荷载,故对PSRCF梁两端均设置弹性垫板,如图6所示。 1.5 收敛准则及负刚度处理 收敛准则是指每次迭代结束后,应检查所得到的解是否在规定的误差范围内。ABAQUS程序采用非平衡力准则对每次迭代结束后非平衡力的相对变化情况进行判别。 框架结构在水平荷载作用下达到极限承载力后,荷载-位移曲线往往会出现下降段,即出现负刚度问题。位移控制法通过控制位移增量来反求荷载增量,能便捷地求得荷载-位移曲线的下降段,较适合本文中对框架的水平单点加载。2 试验验证
2.1 试验概况
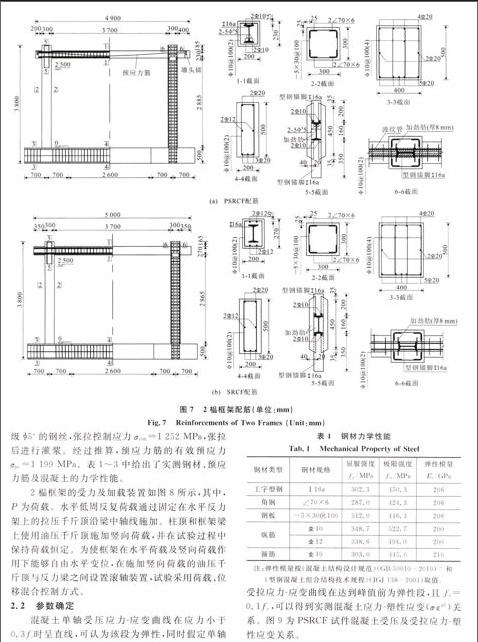
试验中的2榀单层单跨框架PSRCF和SRCF的配筋构造见图7。框架柱剪跨比为5,轴压比为0.1。每榀框架混凝土均分2次浇筑,第1次将混凝土从地梁底部浇筑至框架柱标高为2.5 m处,第2次浇筑梁及节点等剩余部分。节点采用对框架梁内
图7 2榀框架配筋(单位:mm)
Fig.7 Reinforcements of Two Frames (Unit:mm)的工字型钢加焊型钢锚脚的方式[14],可满足钢梁在节点内不发生粘结滑移破坏。预应力筋采用1670级Φ5s的钢丝,张拉控制应力σcon=1 252 MPa,张拉后进行灌浆。经过推算,预应力筋的有效预应力σpe=1 199 MPa。表1~3中给出了实测钢材、预应力筋及混凝土的力学性能。
2榀框架的受力及加载装置如图8所示,其中,P为荷载。水平低周反复荷载通过固定在水平反力架上的拉压千斤顶沿梁中轴线施加。柱顶和框架梁上使用油压千斤顶施加竖向荷载,并在试验过程中保持荷载恒定。为使框架在水平荷载及竖向荷载作用下能够自由水平变位,在施加竖向荷载的油压千斤顶与反力梁之间设置滚轴装置,试验采用荷载、位移混合控制方式。
2.2 参数确定
混凝土单轴受压应力-应变曲线在应力小于0.3fc时呈直线,可认为该段为弹性,同时假定单轴受拉应力-应变曲线在达到峰值前为弹性段,且ft=
计算结果表明:在水平荷载达到峰值荷载之前,选取不同的t0,计算所得骨架曲线几乎重合;达到峰值荷载后,损伤变量的选取对收敛性有重要的影响。通过试算,本文中推荐损伤变量标定参数t0=0.3,此时损伤变量与塑性应变的关系如图10所示。
图10 损伤变量与塑性应变的关系
Fig.10 Relations of Damage Variable and Plastic Strain在低围压作用下,混凝土膨胀角Ψ、流动势偏量ζ、双轴抗压屈服强度与单轴抗压屈服强度之比αf、拉伸子午面上和压缩子午面上的第二应力不变量之比Kc及粘性系数μ对数值计算结果影响较小[15-19],表4中给出了这些参数的常用取值。
2.3 骨架曲线
2榀框架骨架曲线计算值与实测值的比较如图11所示,其中,Δ为位移。由图11可以看出,二者的初始刚度较接近,从承载力来看,数值模拟结果比试验结果大8%左右,吻合良好。
2.4 破坏形态及应变分布
图12为2榀框架模型在水平位移为120 mm时的内部型钢骨架及预应力筋最大塑性应变分布。以工字型钢受拉翼缘屈服作为型钢混凝土梁截面屈服的标志,以受拉角钢全部屈服作为角钢混凝土柱截面屈服的标志。由图12可以看出,框架梁两端受拉区钢梁翼缘、受拉侧预应力筋及柱底部受拉角钢均达到屈服,表明框架在梁端和柱底部出现塑性铰。此外,柱顶角钢未出现屈服,呈现良好的“强柱弱梁”的破坏机制。
为2榀框架模型在水平位移为120 mm时沿竖向和水平方向的混凝土应变分布及破坏形态。由图13可以看出,2榀框架梁端和柱底部受压区混凝土均已被压碎,而且梁端混凝土破坏较柱底部严重,模拟所得的现象与试验基本一致。
图14为塑性铰区型钢应变分布的计算值与实测值的比较,其中,Δ0为位移步长。由图14可以看出,塑性铰区计算应变分布总体把握了实测规律,但是仍存在差别:①屈服前,应变的计算值与实测值较为接近,但是屈服后,计算值与实测值偏差逐渐增大;②计算所得的塑性铰区长度均要比实测值大。其原因可能是数值模拟过程中,混凝土所采用的损伤塑性模型是连续性的,混凝土与钢材之间属于完全粘结、变形协调,而试验中混凝土开裂后已不属于连续介质,裂缝两侧的混凝土与钢材之间将产生一定的相对滑移;此外工字型钢和角钢均采用壳单元,与实际结构也存在一定差别。3 受力全过程分析
为深入研究预应力型钢混凝土组合框架工作机理,本文中对2榀框架在水平荷载作用下的全过程进行了较为细致的数值分析。2榀框架试件的工作机理相似,这里仅给出对PSRCF试件分析的全过程。图15为PSRCF试件不同荷载作用下混凝土和内置型钢骨架最大塑性应变的矢量分布,其中,Pu为极限荷载。图15中混凝土裂缝开裂方向与受拉塑性应变方向垂直,可通过受拉塑性应变表示。
(1)梁柱端初裂。从图15(a)可知,裂缝最先出现在梁左端上部,且为弯曲裂缝。其原因是在水平荷载和竖向荷载共同作用下,梁左端上部所受弯矩最大所致,此时水平荷载大小约为0.07Pu。当水平荷载达到0.15Pu时,左柱底部右侧受拉区混凝土出现弯曲裂缝,如图15(b)所示。
(2)屈服过程。如图15(c)所示,当水平荷载达到0.72Pu时,梁左端内置型钢上翼缘和左柱底部角钢外侧面均达到了屈服应变,此时梁柱端所有受拉区也均出现弯曲裂缝。对于预应力构件,其节点区也有斜裂缝出现[图15(d)],这与试验现象较为一致。
当水平荷载达到0.84Pu和0.90Pu时,左柱和右柱下端的受拉角钢将先后完全屈服,如图15(e),(f)所示。当水平荷载增至0.97Pu时,梁右端型钢下翼缘也达到了屈服,见图15(g)。
(3)极限状态。极限状态下框架混凝土和内置型钢骨架最大塑性应变分布如图15(h),(i)所示。可以发现,梁左端下侧混凝土已被压碎,梁端受压区型钢翼缘和柱底部受压角钢外缘也均达到屈服。
(4)破坏状态。当水平荷载下降至0.85Pu时,梁端及柱底部受压区混凝土均被压碎,见图15(j)。
通过分析可以发现,塑性铰首先出现在梁端,紧接着在两柱底部出现,最后出现在另一梁端。究其原因在于:套建增层框架底层较高,将在柱底部产生较大弯矩,并对底层框架的出铰顺序产生不利的影响。此外,混凝土首次被压碎时刻出现在极限荷载之前且接近极限荷载,位置出现在框架梁端,因而框架最大承载力可以用框架梁端混凝土被压碎作为计算的标志。4 参数分析
为进一步研究此类框架的力学性能,本文中从柱轴压比n0、柱含钢率ρa、梁型钢截面抵抗矩Wss、梁纵筋配筋率ρs、预应力度λ及柱长细比β等方面对框架的骨架曲线进行考察。
框架柱的截面尺寸为300 mm×300 mm,其对称布置4个角钢;非预应力框架梁跨度为4 000 mm,截面尺寸为200 mm× 270 mm,工字型钢居中对称布置,纵筋上下对称布置;预应力框架梁跨度为4 000 mm,截面尺寸为200 mm×230 mm,工字型钢居中对称布置,纵筋上下对称布置。本文中只给出预应力框架的计算结果,非预应力框架与此类似。
图16(a)为柱轴压比n0对骨架曲线的影响。随着轴压比的增大,骨架曲线峰值荷载先增大后减小,峰值荷载对应的位移减小,下降段变陡,延性变差。图16(b)为柱含钢率ρa对骨架曲线的影响。随着柱含钢率的增加,骨架曲线的初始刚度略有增大,峰值荷载增加,下降段曲线斜率接近,曲线形状相同。图16(c)为梁型钢截面抵抗矩Wss和配筋率ρs对骨架曲线的影响。随着型钢截面抵抗矩和配筋率的增加,骨架曲线初始刚度略有增加,峰值荷载提高,峰值荷载对应的位移略有增大,骨架曲线形状相似。图16(d)为预应力度λ对骨架曲线的影响。可以看出,预应力度的增大能略微提高骨架曲线的初始刚度,增大框架水平承载力。图16(e)为柱长细比β对骨架曲线的影响。随着柱长细比的增大,骨架曲线峰值荷载减小,峰值荷载对应的位移增加,下降段变平缓。
5 结 语
(1)数值模拟结果如骨架曲线、破坏形态、梁柱端应变分布与试验结果基本吻合,数值模拟结果比试验结果大8%左右,验证了本文中所选择材料模型、计算单元和相关参数的合理性。
(2)分析所得框架梁两端受拉区钢梁翼缘和柱底部受拉角钢均达到屈服,而柱顶角钢均未屈服,说明框架在梁端和柱底部出现塑性铰并呈现良好的“强柱弱梁”的破坏机制。
(3)采用此类结构形式的套建增层框架,将在柱底部产生较大弯矩,并且对底层框架的出铰顺序产生影响。
(4)参数分析表明,柱轴压比和长细比对骨架曲线影响最大。轴压比增大,骨架曲线峰值荷载先增大后减小,峰值荷载对应的位移减小,延性降低;长细比增加,结构刚度降低,峰值荷载减小,延性增大。
参考文献:
References:
[1] 傅传国,李玉莹,孙晓波,等.预应力及非预应力型钢混凝土框架受力及抗震性能试验研究[J].建筑结构学报,2010,31(8):15-21.
FU Chuan-guo,LI Yu-ying,SUN Xiao-bo,et al.Experimental Study on Seismic Performance of Preftressed and Non-prestressed Steel Reinforced Concrete Frames[J].Journal of Building Structures,2010,31(8):15-21.
[2]熊学玉,高 峰.预应力型钢混凝土框架试验研究及分析[J].四川大学学报:工程科学版,2011,43(6):1-8.
XIONG Xue-yu,GAO Feng.Experimental Investigation and Analysis on Large Scale Prestressed Steel Reinforced Concrete Frame[J].Joural of Sichuan University:Engineering Science Edition,2011,43(6):1-8.
[3]王 琨,袁沈峰,曹大富,等.配置核心钢管的钢筋混凝土柱-钢骨混凝土梁组合框架抗震性能试验研究[J].建筑结构学报,2013,34(6):103-112.
WANG Kun,YUAN Shen-feng,CAO Da-fu,et al.Test on Seismic Performance of Frame Structure of Steel Reinforced Concrete Beam and Steel-tube Encased Concrete Column[J].Journal of Building Structures,2013,34(6):103-112.
[4]郑文忠,王 英,刘思嘉.哈尔滨南岗会堂增层改造设计[J].哈尔滨工业大学学报,2012,44(6):45-50.
ZHENG Wen-zhong,WANG Ying,LIU Si-jia.Structure Design for Adding Storeys of Harbin Nangang Hall[J].Journal of Harbin Institute of Technology,2012,44(6):45-50.
[5]郑文忠,王 琨.型钢混凝土梁-角钢混凝土柱框架抗震性能试验研究[J].土木工程学报,2011,44(3):49-60.
ZHENG Wen-zhong,WANG Kun.Study of Seismic Performance of Frame Structures of Steel Reinforced Concrete Beams and Angle-steel Concrete Columns[J].China Civil Engineering Journal,2011,44(3):49-60.
[6] ABAQUS Inc.ABAQUS Standard Users Manual:ABAQUS 6.5 Theory Manual[M].Providence:Hibbitt,Karlsson & Sorensen,Inc.,2005.
[7]LUBLINER J,OLIVER J,OLLER S,et al.A Plastic-Damage Model for Concrete[J].International Journal of Solids and Structures,1989,25(3):299-326.
[8]DRUCKER D C,PRAGER W.Soil Mechanics and Plastic Analysis or Limit Design[J].Quarterly of Applied Mathematics,1952,10(2):157-165.
[9]GB 50010—2010,混凝土结构设计规范[S].
GB 50010—2002,Code for design of concrete structures[S].
[10]王金昌,陈页开.ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社,2006.
WANG Jin-chang,CHEN Ye-kai.Application of ABAQUS in Civil Engineering[M].Hangzhou:Zhejiang University Press,2006.
[11]张昊宇,郑文忠.1860级低松弛钢绞线高温下力学性能[J].哈尔滨工业大学学报,2007,39(6):861-865.
ZHANG Hao-yu,ZHENG Wen-zhong.Mechanical Property of Steel Strand at High Temperature[J].Journal of Harbin Institute of Technology,2007,39(6):861-865.
[12]ABAQUS Inc.ABAQUS有限元软件6.4版入门指南[M].庄 茁,译.北京:清华大学出版社,2004.
ABAQUS Inc.Infinite Element Soft ABAQUS 6.4 Manual[M].Translated by ZHUANG Zhuo.Beijing:Tsinghua University Press,2004.
[13]郭 楠,郑文忠.板-柱结构抗震性能研究[J].沈阳建筑大学学报:自然科学版,2008,24(5):729-736.
GUO Nan,ZHENG Wen-zhong.Seismic Behavior of Plate-column Structure[J].Journal of Shenyang Jianzhu University:Natural Science,2008,24(5):729-736.
[14]赵鸿铁.钢与混凝土组合结构[M].北京:科学出版社,2001.
ZHAO Hong-tie.Steel and Concrete Composite Structure[M].Beijing:Science Press,2001.
[15]雷 拓,钱 江,刘成清.混凝土损伤塑性模型应用研究[J].结构工程师,2008,24(2):22-27.
LEI Tuo,QIAN Jiang,LIU Cheng-qing.Application of Damaged Plasticity Model for Concrete[J].Structural Engineers,2008,24(2):22-27.
[16]卫 星,肖 林,邵柯夫,等.钢-混组合结构PBL剪力键疲劳寿命试验[J].中国公路学报,2013,26(6):96-102.
WEI Xing,XIAO Lin,SHAO Ke-fu,et al.Fatigue Performance of Perfobond Shear Connector in Steel-concrete Composite Structure[J].China Journal of Highway and Transport,2013,26(6):96-102.
[17]荣学亮,黄 侨,赵 品.考虑疲劳损伤的栓钉连接件抗剪承载力研究[J].中国公路学报,2013,26(4):88-93,101.
RONG Xue-liang,HUANG Qiao,ZHAO Pin.Study on Shear Capacity of Stud Connectors Subjected to Fatigue Damage[J].China Journal of Highway and Transport,2013,26(4):88-93,101.
[18]刘 鸣,刘伯权.钢筋混凝土柱低周疲劳力学性能分析[J].长安大学学报:自然科学版,2012,32(5):65-70.
LIU Ming,LIU Bo-quan.Low-cycle Fatigue Damage for Shear Behavior of Reinforced Concrete Columns[J].Journal of Changan University:Natural Science Edition,2012,32(5):65-70.
[19]袁春燕,卢俊龙.基于结构解释模式的服役混凝土结构损伤识别[J].长安大学学报:自然科学版,2014,34(4):77-81.
YUAN Chun-yan,LU Jun-long.Damage Identification in Concrete Structure Based on Interpretative Structural Model[J].Journal of Changan University:Natural Science Edition,2014,34(4):77-81.
