海水声速快速高精度测量方法*

乔纯捷,王跃科,黄志刚

(国防科技大学 机电工程与自动化学院, 湖南 长沙　410073)



海水声速快速高精度测量方法*

乔纯捷,王跃科,黄志刚

(国防科技大学 机电工程与自动化学院, 湖南 长沙410073)

摘要：为实现对海水声速快速、高精度的测量，采用一种系统结构简单的声速测量方案。通过连续波信号参数估计的方法实现了对声传播时间和声速值的测量。采用伪随机序列对连续波进行调制处理，解决了单频连续波信号在测量中存在的整周期模糊与回波干扰问题。通过构建声速试验平台，进行了系统校准与测量试验。试验结果表明该方法具有测量精度高、响应快速的优点，适合于在水下机动平台上对海洋声速剖面进行快速、高精度的测量。

关键词：声速;声传播时间;回波干扰;伪随机序列;不确定度;系统校准

声速是海洋中重要的声学量之一，是影响声波在海洋中传播的最基本的物理参数。及时、准确地获取海水声速，特别是声速随时间、空间的变化情况，对水下各种工程实践和理论研究都具有非常重要的意义。

目前，在海洋环境下能够实现的声速测量精度可以达到10-5量级[1]。Trusler在其著作[2]中，将声速测量的试验方法分为稳态测量技术与瞬态测量技术两大类。在声速测量试验中常用的脉冲回波重合法、脉冲叠加法等属于前者，这些技术可以获得最高10-6量级的测量精度[3]，但试验过程需要使用复杂、精密的测量系统。试验中为了建立稳态条件，往往需要对信号频率(或发射周期、扫描频率)进行不断的反馈调节，测量过程持续时间长，无法在海洋环境中使用。目前在海水中实际应用的声速仪普遍采用“环鸣法”，该方法属于瞬态测量技术，其设备结构简单、测量过程无须调整[4]。声速仪在工作时为了抑制噪声影响同时降低系统对延时测量分辨率的要求，需要循环发射声信号，这使得测量时间加长，动态性能变差。文献[5]指出，由于受多次信号反射导致的相位误差等因素的影响，传统的环鸣法的测量准确度很难超过0.25m/s。

1基于连续波参数估计的声速测量方法

1.1　基本原理

连续波信号具有较强的干扰抑制能力，适合于精密测量应用，所提声速测量方法来源于对单频正弦信号的相位估计。测量中使用一组固定安装的声换能器，如图1所示，发射换能器A输出的测量信号被接收换能器B接收后，通过信号处理得到声传播时间τ，然后利用式(1)得到声速值。

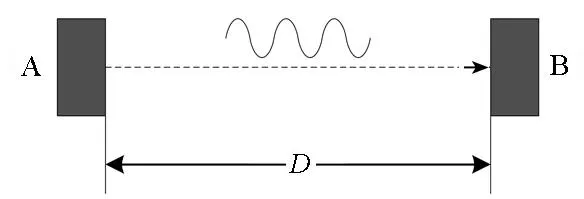
图1　连续波声速测量原理示意图Fig.1　Principle of sound speed measurements using continuous wave

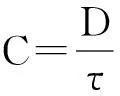
(1)

信号发送端发射单频连续波：

x(t)=Acos(Ω0t)

(2)

接收信号可表示为：

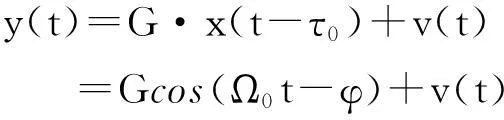
(3)

其中：A为信号的幅度；Ω0表示发射信号的角频率；D为声传播距离，C为声速；G为接收信号的幅度；τ0=D/C表示声传播延迟，v(t)表示测量噪声，φ表示由于声传播时间导致的信号相位变化。其中，

φ=Ω0τ0

(4)

由于信号频率已知，可以通过接收信号的相位信息得到声传播时间，并在声传播距离已知条件下得到声速值。正弦连续波信号的参数估计已有成熟的理论，根据参考文献[6]，当采样点足够多时，用一系列离散采样值进行相位估计的方差下限为(其中N为样点数)：

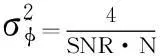
(5)

采用离散傅里叶转换(Discrete Fourier Transform,DFT)方法进行相位估计，在保证整个测量过程时间同步且信号处理过程中不发生频谱泄漏的条件下，估计结果接近方差下限。结合式(1)、式(4)和式(5)可以得到声速测量方差为：

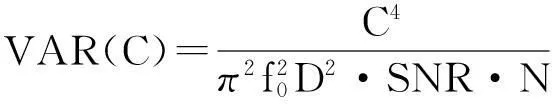
(6)

式(6)表明，在发射功率与信噪比一定的条件下，可以通过增加观测信号的样点数来获得更高的测量精度。

1.2　存在问题

利用单频正弦信号的相位估计实现声速测量的方法比较简单，但需要解决2个问题：

问题1：相位多值模糊问题[7]。由于接收信号相位φ通过计算后变化范围为[0,2π)，为得到测量相位与声速之间的一一映射关系，被测声速范围被限制在很小的区间内，很难适应实际应用过程中声速的变化范围。

问题2：回波干扰问题。如图2所示，发射信号到达接收端时除一部分被接收端吸收外，还有一部分能量会在收发换能器端面之间来回反射。由于两个换能器间距较小，经过两次反射的回波信号仍具有较强的能量，与直达信号在接收换能器端面叠加，会对测量结果产生影响。

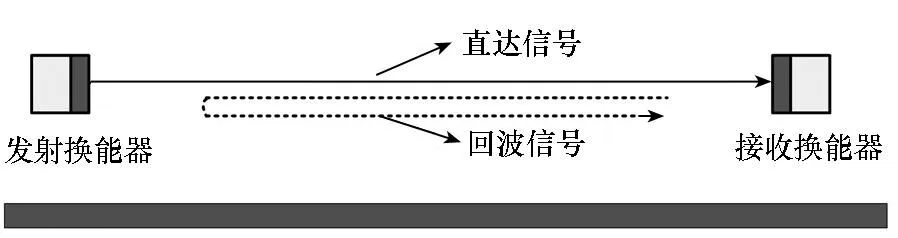
图2　回波产生示意图Fig.2　Schematic of the multiple reflections

对于单频发射信号，不考虑噪声的情况下，接收信号可表示为：

(7)

式中：K表示回波次数；φi≈(2i+1)φ表示第i次回波的相位。

随着回波次数i的增大，回波信号衰减增大，为方便分析，仅考虑i=1的情况，有：

y(t)=GAcos(Ω0t-φ)+G1Acos(Ω0t-φ1)

(8)

此时接收信号的相位估计偏差最大值为：

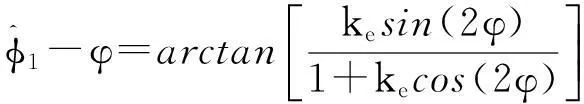
(9)

2采用伪随机信号调制的声速测量方法

2.1　原理

伪随机码由于其良好的性能和易实现等特点而得到了广泛的应用[8]。伪随机序列具有尖锐的自相关特性，使用经伪随机序列调制的单频信号作为声速测量信号，可以通过对接收信号相关峰的位置检测得其到达时间，该时间可用于消除相位模糊的影响。此外，通过合理选择伪随机序列中的码片宽度，使直达信号与回波信号到达接收换能器的时间间隔大于1个码片，可以有效抑制回波信号对载波相位估计的影响。

2.2　周期模糊问题的解决方法

本方法使用的伪随机序列为最大长度线性移位寄存器序列(m序列)，记为m(t)，则发射信号可表示为：

x(t)=m(t)Acos(Ω0t)

(10)

不考虑噪声与回波的情况，经过τd的延迟后，接收信号可表示为：

y(t)=GA·m(t-τd)cos[Ω0(t-τd)]

(11)

则收发信号的互相关函数为：

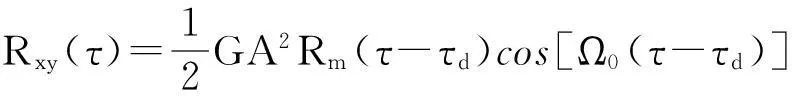
(12)

式中，Rm(τ)表示伪随机序列的自相关函数，其表达式为：

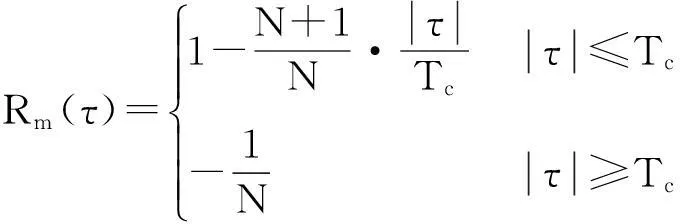
(13)

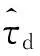
2.3　多次回波干扰问题分析

通过系统参数设计，可以将回波信号的到达时间与直达信号的到达时间之差控制在1个码片以上，从而可以避免回波信号对直达信号相关峰位置测量的影响。下面分析回波信号对直达信号载波相位测量的影响。

为求得载波相位必须要解调接收信号，而解调过程恰好能够有效抑制回波干扰。仍以式(8)所示的信号为例，存在回波干扰的接收信号可表示为：

y(t)=GA·m(t-τd)cos[Ω0(t-τd)]+

G1A·m(t-τd′)cos[Ω0(t-τd′)]

(14)

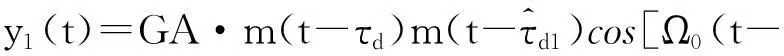
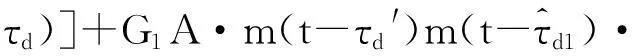
cos[Ω0(t-τd′)]

(15)

y1(t)≈GAcos[Ω0(t-τd)]+

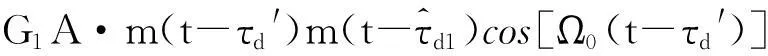
(16)

可以通过对解调后的信号的频谱分析实现载波相位的测量。如图3所示，经过解调后，直达信号恢复为单频信号，在信号频谱的观测频点上信号谱峰高度提升了N倍；而回波信号的频谱仍然类似于噪声信号，落在被测频点谱线位置的信号能量基本没有变化。

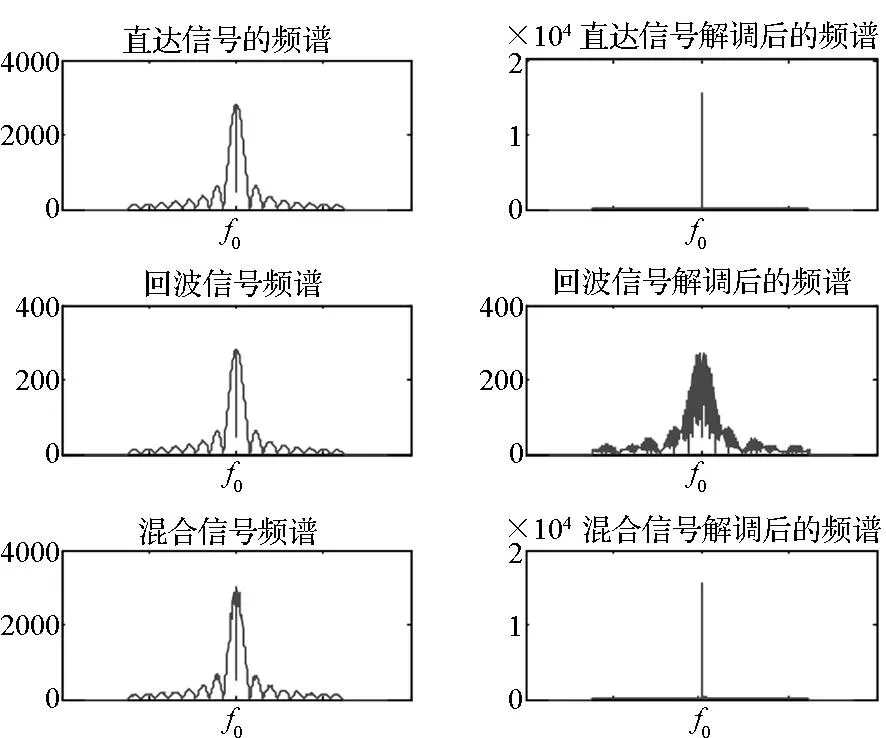
图3　解调前后信号频谱对照图Fig.3　Comparison between modulated and demodulated signal spectrum

此时，直达信号的相位估计结果受回波信号的影响如式(17)所示：

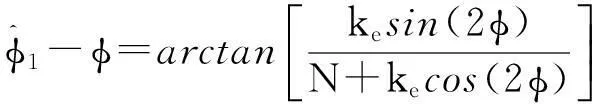
(17)

由于ke<1，N≫1，比较式(17)与式(9)，采用伪随机信号调制后的连续波信号进行声速测量，回波导致的信号相位估计偏差明显变小，回波干扰对测量结果的影响得到有效抑制。

3声速测量试验与分析

3.1　声速测量系统的构建

本文构建的声速测量试验系统如图4所示，一对固定安装的声换能器放置在测量水槽中，传输介质为蒸馏水。信号合成处理模块输出的测量信号经发射换能器转换为超声信号向水中辐射，接收换能器将收到的声信号转换为电信号，再经信号调理与模数转换后得到接收信号的采样序列，由计算机进行处理后得到测量结果。

试验采用的测量信号采用码长N=31、码片速率为10kbps的m序列对频率为1MHz的单频连续信号进行调制。试验中ke约为0.1，根据式(17)可以得到由回波引入的载波相位估计偏差最大值约为3.2×10-3(弧度)。此时对于1MHz的单频载波延时测量偏差约为0.05ns，根据式(1)可得其对声速测量结果的影响小于1mm/s，表明回波干扰对声速测量结果的影响得到了有效的抑制。

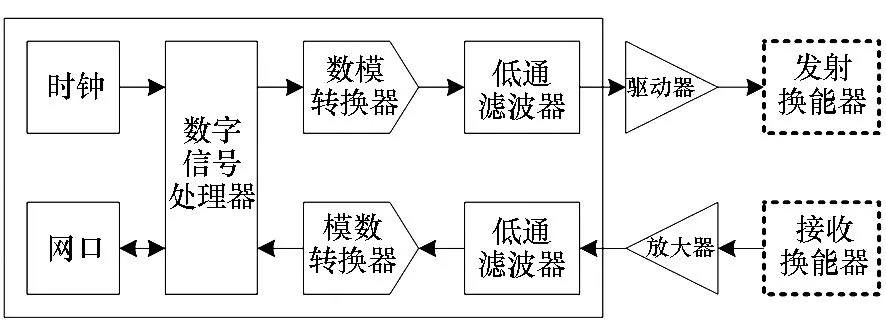
图4　声速测量试验系统结构图Fig.4　Architecture diagram of sound-speed measurement system

3.2　系统校准

在声速测量中，声传播距离D、系统群延时都会对测量结果产生影响。而这两个参数很难在系统的生产、加工过程中保证其准确度，通常需要通过系统校准的方式得到[9]。采用的方法是通过精确控制蒸馏水的温度，利用声速与温度的函数关系式来得到准确已知的声速值，实现系统校准。试验中温度计的精度为0.01℃，采用的温度、声速换算公式为Del Grosso公式[10]。

仅考虑试验温度与系统群延时的情况下，声传播时间与系统参数的关系可以表示为：

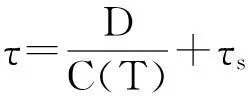
(18)

式中，C(T)为某一温度条件下对应的声速，τ为通过测量得到的声传播时间，τs为系统群延时。

以7个温度点对应的延时估计结果作为τ的观测向量Y，Y=[τ1,τ2,…,τ7]T；由D，τs组成待估参数向量X，X=[D,τs]T；采用Del Grosso公式计算的声速值C(T)作为声速观测值，并建立观测矩阵H，则参数方程可表示为：

Y=HX

(19)

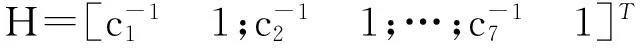
采用最小二乘法，则系统参数的校准结果为：

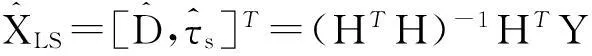
(20)

另外，为了评价校准结果，需要计算D，τs的合成不确定度，可按式(21)、式(22)计算：

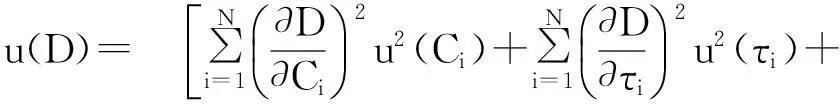
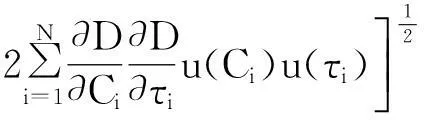
(21)

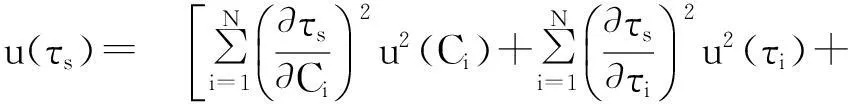
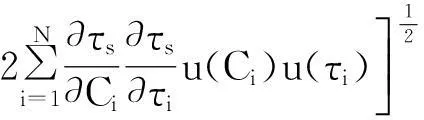
(22)

其中，u(Ci)表示声速的合成不确定度，由温度Ti的测量不确定度以及声速换算公式本身的不确定度组成，其计算如式(23)所示：

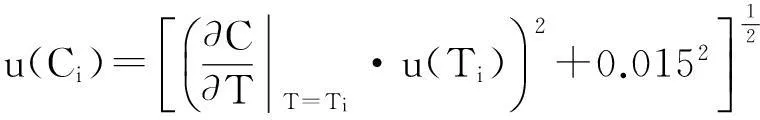
(23)

根据试验数据，得到的系统参数校准结果及其不确定度如表1所示。

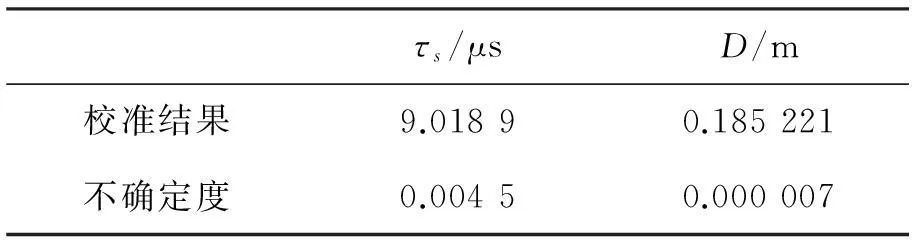
表1　系统参数标定结果

3.3　系统校准与声速测量试验

利用系统校准参数及延时测量结果，按照式(24)就可以实现声速的测量。

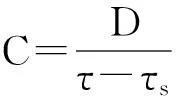
(24)

声速测量的准确度仍利用合成不确定度来评价，其计算公式如式(25)所示：

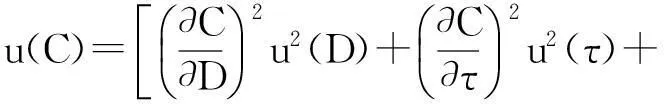
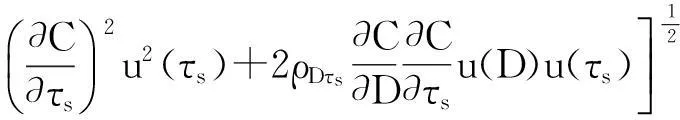
(25)

式中，D表示基线长度、τ表示声传播时间，τs表示群延时；ρDτs为D与τs间的相关系数。系统在总共13个温度点下进行了声速测量试验，计算得到的声速测量结果及其不确定度，如表2所示。图5是在不同温度条件下，试验得到的声速值与Del Grosso公式换算声速的偏差情况。

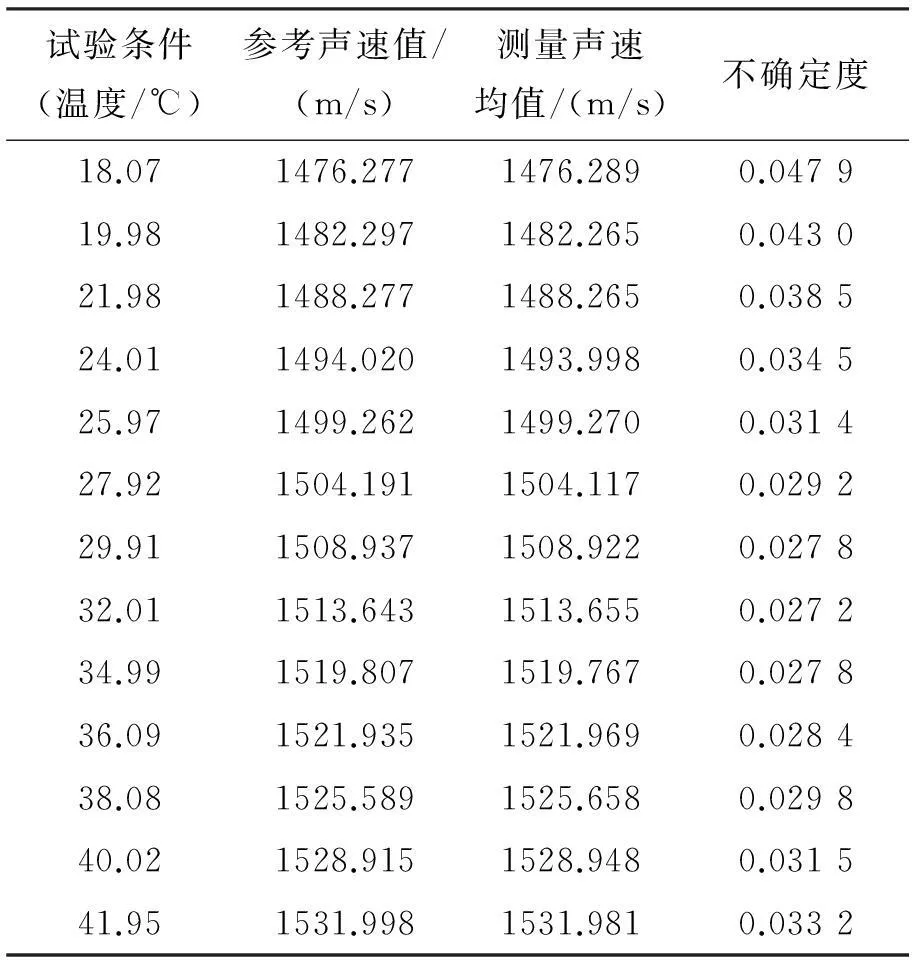
表2　声速测量结果及其不确定度

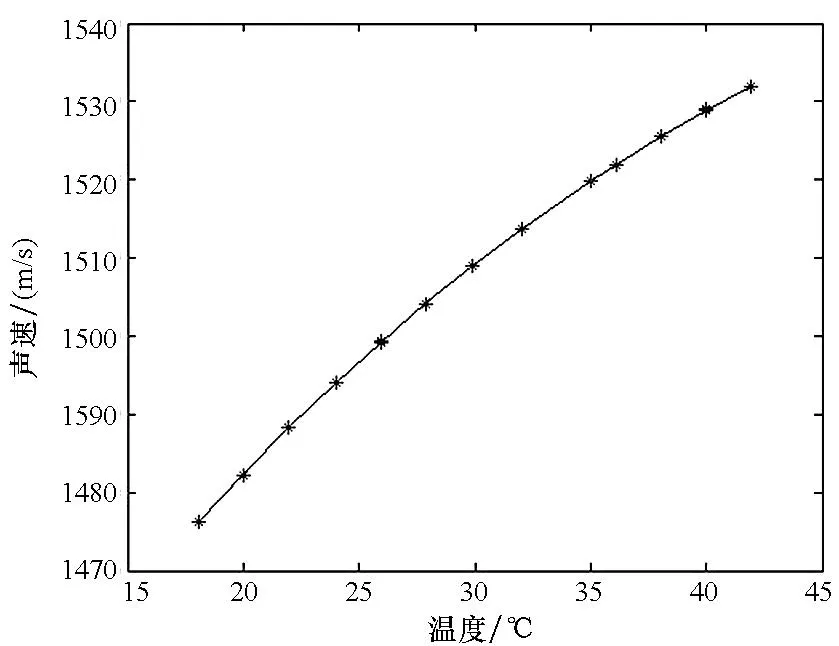
(a)声速测量值随水温变化情况(a) Changes of sound-speed along with water temperature

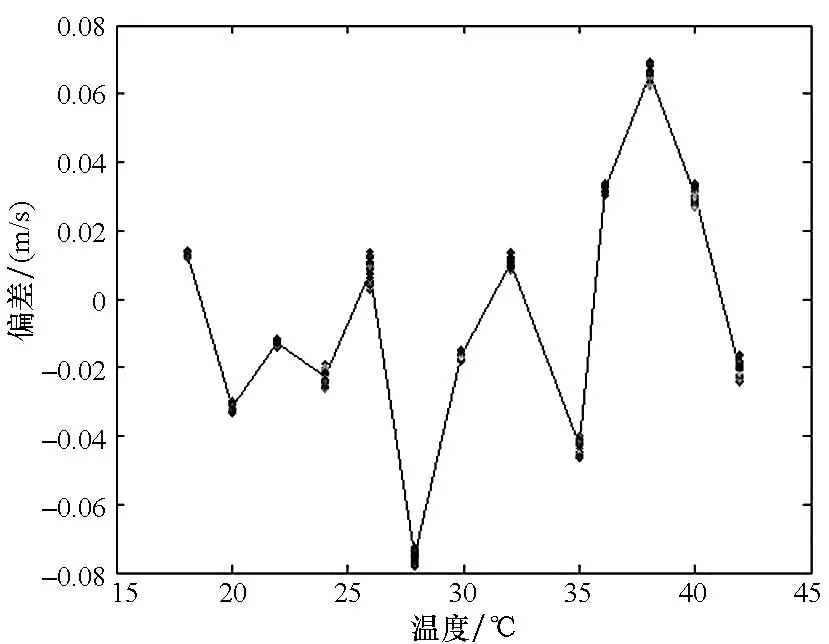
(b)测量声速与参考声速的偏差(b) Sound-speed deviation between measured value and the referential value图5　声速测量结果与Del Grosso经验公式换算值的对比 Fig. 5　Sound-speed comparison between measured results and equivalent value of Del Grosso′s formula

4结论

研究与试验结果表明，采用伪随机序列调制的连续波信号进行声速测量，对随机干扰和回波干扰具有较强抑制能力，可用简单的系统结构实现精密的声速测量。试验结果与目前国际主流声速仪处于同一量级(10-5)，通过对表1的系统校准结果和式(25)中各参数对声速测量结果的贡献率的分析表明系统参数的校准结果是影响测量结果不确定度的主要原因。如果采用更加稳定的系统结构与更为理想的校准条件，系统的声速测量性能还有较大的提升潜力。采用数字信号处理平台进行信号的实时处理时，单次测量时间小于5ms，测量速度较当前主流声速仪产品(测量时间约为100ms)提高了1个数量级以上，具备了快速测量能力。

参考文献(References)

[1]Sweeney A D, Spiess F N, Boegeman D E, et al. The MPL sound velocimeter: an instrument for in situ sound velocity measurements in the deep ocean[J]. The Journal of the Acoustical Society of America, 1997, 102(5): 3119.

[2]Trusler J P M. Physical acoustics and metrology of fluids[M]. UK:Adam Hilger， 1991: 179-234.

[3]Papadakis E P. Absolute accuracy of the pulse-echo-overlap method and pulse-superposition method for ultrasonic velocity[J]. The Journal of the Acoustical Society of America, 1972, 52(3B): 843.

[4]赵先龙. 声速仪的设计[J]. 海洋测绘， 2002， 22(1): 54-56.

ZHAO Xianlong. Design of sound velocimeter[J]. Hydrographic Surveying and Charting, 2002, 22(1):54-56.(in Chinese)

[5]Eaton G，Dakin D T. Miniature time of flight sound velocimeter offers increased accuracy over sing-around technology and CTD instrumentation[C]//Proceedings of the Oceanology International′96 Conference, 1996：55-64.

[6]齐国清. 离散实正弦信号参数估计的Cramer Rao方差下限[J]. 数据采集与处理, 2003, 18(2):151-155.

QI Guoqing. Cramer Rao bounds of real sinusoid parameter estimation from discrete-time observation[J]. Journal of Data Acquisition & Processing, 2003,18(2):151-155.(in Chinese)

[7]Jacobs E， Ralston E W. Ambiguity resolution in interferometry[J]. IEEE Transactions on Aerospace and Electronic Systems, 1981, AES-17(11):766-780.

[8]顾冬梅, 茅玉龙. 伪随机二相码连续波信号参数估计算法[J]. 雷达与对抗, 2009, 3:16-18.

GU Dongmei, MAO Yulong. A parameter estimation algorithm of pseudo random biphase-coded CW signals[J]. Radar & Ecm, 2009, 3:16-18.(in Chinese)

[9]Sweeney A D， Chadwell C D，Hildebrand J A. Calibration of a seawater sound velocimeter[J]. IEEE Journal of Oceanic Engineering, 2006, 31(2): 454-461.

[10]Del Grosso V A， Mader C W. Speed of sound in pure water[J]. The Journal of the Acoustical Society of America， 1972, 52(5B): 1442-1446.

http://journal.nudt.edu.cn

Fast and precise measurement method of sound velocity in seawater

QIAOChunjie,WANGYueke,HUANGZhigang

(College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, China)

Abstract：The velocity of sound is one of the important acoustic parameters in ocean. For realizing rapid and high-precision measurements of seawater sound velocity, a sound velocity measurement method whose system architecture is simple was adopted.The measurements of sound propagation time and velocity value were achieved by continuous wave signal’s parameter estimation method. A pseudo-random sequence was introduced to modulate and handle continuous waves, which overcame the cycle ambiguities and echo interference problems of single-frequency signal in measurement. A sound velocity measurement platform was built to conduct system calibration and measurement experiment. Experiment results show that this method has high accuracy and fast response and is suitable for ocean sound velocity profile measurement on subaqueous mobile platform.

Key words：sound velocity; sound propagation time; echo interference; pseudo-random sequence; uncertainty; system calibration

中图分类号：TH73

文献标志码：A

文章编号：1001-2486(2015)06-162-05

作者简介：乔纯捷(1975—)，男，陕西宝鸡人，副研究员，博士研究生，E-mail: qiaoxj@nudt.edu.cn

基金项目：国家自然科学基金资助项目(61273347)

收稿日期：*2014-11-03

doi:10.11887/j.cn.201506029