半球之间的引力
2015-02-01邱为钢
邱为钢
(湖州师范学院理学院, 浙江 湖州 313000)
半球之间的引力
邱为钢
(湖州师范学院理学院, 浙江 湖州313000)
摘要两个不同半球沿对称轴方向(第1种情形)或者接触面分开(第2种情形),球心间的距离是h.在情形1中,计算得到了展开到h一次项的引力势能表达式.由这个引力势能的解析表达式,得到了两个半球间的引力表达式.在情形2中,计算得到了展开到h二次项的引力势能表达式.当大的半球固定时,小的半球作简谐振动,并给出了周期公式.以上的解析式得到了数值计算值的验证.
关键词万有引力;半球;周期
基金资助: 国家自然科学基金(11275067,11475062).
第一颗原子弹的研发过程中, 有这样一个故事: 某次试验, 不小心两个铀半球合在一起, 马上就要重合超过临界质量,将发生核反应.有位物理学家眼捷手快, 把两个半球分开,阻止了一次严重事故. 撇开故事,现在只考虑半球之间的引力(平方反比关系), 掰开两个半球的力量有多大? 这就是本文主要讨论的问题.
设两个半球的半径分别为R1,R2,不失一般性,设R1>R2.起始时球心重合,重合面为x-y平面.设大球固定,小球拉开.为计算方便,只考虑两种情况,一是沿z轴方向拉开一段距离;二是沿着重合面(假设接触面完全光滑)拉开一段距离.第二种情况下,如果拉开距离是小量的话,小球就在平衡位置作小幅度的简谐振动.那么,这个振动周期是多少?为便于计算,假设球心距离h远小于两球的半径,计算过程中只展开到h的一阶或两阶小量.

图1 半球坐标示意图
设大球在下面,其中一点的球坐标是(r1,θ1,φ1),参数满足π/2<θ1<π;小球在上面,其中一点的球坐标是(r2,θ2,φ2),参数满足0<θ2<π/2.设两个球的质量密度分别是ρ1,ρ2,由万有引力势能公式, 两球之间的引力势能是

(1)
式(1)中的积分因子有积分变换式


(2)
其中,波矢量k的球坐标是(k,θ3,φ3).式(2)中积分因子的分子有以下展开式[1,2]
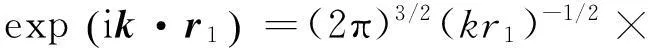
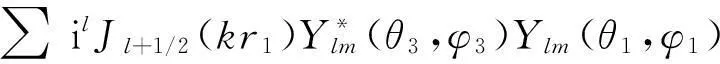
(3)
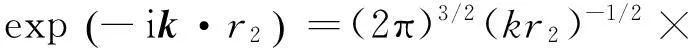

(4)
只考虑到h的一阶,那么有


(5)
把式(3)~式(5)代入式(2), 计算得到(具体计算过程请参阅文献[3])引力势能中包含h一次方项为
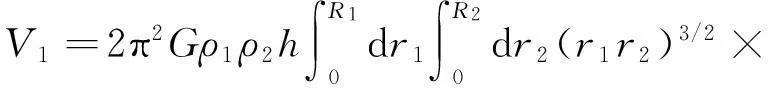

(6)
由积分公式[1,2]

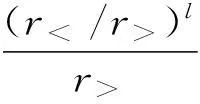
(7)
计算得到

(8)
由此得到沿对称轴方向掰开两个半球的力是
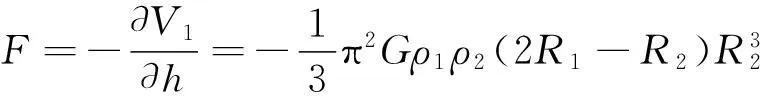
(9)
下面讨论沿接触面的滑动,设沿x轴方向移动h距离,考虑到h的一阶和二阶:
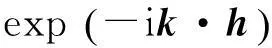

(10)
把式(3),式(4)和式(10)代入式(2), 由对称性,平移距离h一次方贡献为零,即沿切合面方向掰开半球所需力为零.引力势能中包含h二次方项分为V2,0和V2,2(具体计算过程请参阅文献[3]),其中V2,0的表达式是
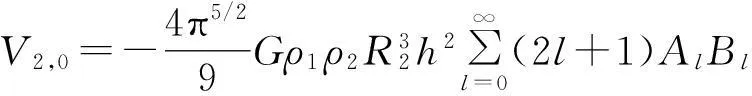
(11)
其中,

(12)
V2,2的表达式是
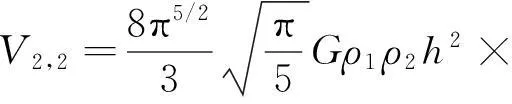
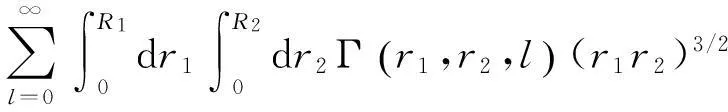
(13)
其中,
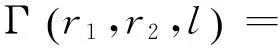


(14)
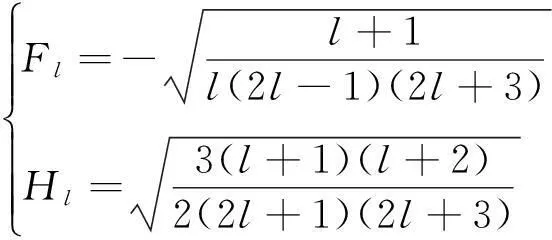
(15)

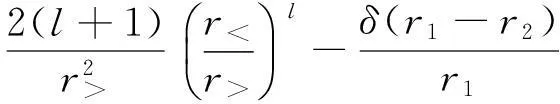
(16)
实际计算中,只取前4项求和,即l=0,1,2,3这4项, 这时两半球引力势能的二次项是

(17)
式(17)表明小的半球所感受到的引力势能是二次项势能,也意味着小球沿切面作简谐运动.由二次方势能中简谐运动的周期公式,计算得到
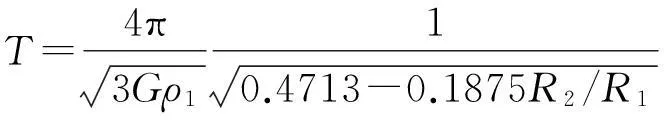
(18)

表1 两球引力势能的二次项比例系数
综合利用数学物理的积分求和和特殊函数公式,给出了两个半球垂直拉开和平行拉开时引力势能的近似解析表达式,结果与数值求值一致.也给出了小球沿切面作简谐运动周期的表达式.
参考文献
[1]王竹溪,郭敦仁.特殊函数概论[M].北京: 北京大学出版社,2000.
[2]Gradshteyn I S, Ryzhik I M. Table of integrals, series, and products[M].7版. 北京: 世界图书出版公司,2008.
[3]邱为钢.数学物理专题选讲[Z]. 湖州: 湖州师范学院,2014.
审稿意见摘录:
文中的两个例子,吸引力和简谐频率可以有解析解,对于多数大学物理的学生和教师来说,是一件新鲜事.可以作为复杂的习题、大作业之类.文中讨论的内容,不是当下教学的急所,但可以拓宽大学物理师生的视野,本身也有点新意.
■
GRAVITATION BETWEEN TWO HEMISPHERES
Qiu Weigang
(School of Science, Huzhou Teachers College, Huzhou, Zhejiang 313000)
AbstractTwo different hemispheres are separated from each other along symmetric axis (case one) or a contact plane (case two). The distance between their centers is denoted as h. In the case one, the gravitational potential energy containing first order of h is derived. The attraction force between two hemispheres is obtained from the analytical expression of the gravitational potential energy. In the case two, the gravitational potential energy containing second order of h is derived. When the bigger hemisphere is fixed, the smaller one’s motion is a simple harmonic vibration. The period time is given. All of those analytical expressions are confirmed by numerical calculation results.
Key wordsgravitation; hemisphere; period
作者简介:2014-12-23 邱为钢, 男,副教授,主要从事数学物理的教学和研究.wgqiu@hutc.zj.cn
