电弧铣削电极损耗及补偿研究

陈风帆，刘 晓，王 炜

（上海航天设备制造总厂，上海200245）

电弧铣削[1-2]是通过电弧放电产生大量的热来蚀除材料的非接触式加工方法，由于其功率密度远高于传统电火花加工，且不受接触力及材料硬度的影响，具有优质、高效、低耗等特点，因此在难切削材料的高效加工领域具有独特的优势，被广泛用于航空航天及汽车制造等行业。

在电弧铣削过程中，放电间隙内的电子会对阳极产生轰击作用，这将导致电极发生损耗，其损耗量远远大于机械加工的磨损量。同时，电极的损耗会使其外形发生改变，严重影响了加工精度与零件表面质量。因此，有必要在加工过程中对电极损耗进行补偿。为此，本文构建了电极蚀除形状模型，经过神经网络的训练，建立了工艺参数与蚀除量的关系，提出了电极轴向与径向损耗预测补偿的方案，为进一步提高加工效率与精度提供了理论基础。

1 电极损耗分析

电弧加工的本质是在工具电极和工件之间形成放电通道，通道内产生能量密度极高的极间电弧作用于工件表面，引起高温高压，使工件材料熔化乃至气化，从而实现材料的高效去除，以达到零件形状、尺寸的设计加工要求。同时，随着工件材料被去除，工具电极不可避免地会产生损耗[3]。

以图1所示的电极为例，该电极为多孔电极，在其边缘处损耗较多，超过加工深度后，电极基本不存在蚀除。这是由于在电极边缘处，电荷聚集较多，存在尖端放电现象，附近电位较高，加速了蚀除的进行；而超过加工深度的部分不存在放电通道，没有电弧作用，因此不发生蚀除。

图1 电极损耗图

针对电极周围的电位问题，建立静电场的泊松方程：

当场域为Ω时，其等价泛函为：

将场域Ω离散化，划分为多个体积单元，且将每个单元内的电位分布近似认为线性变化，从而可将式（2）化为：

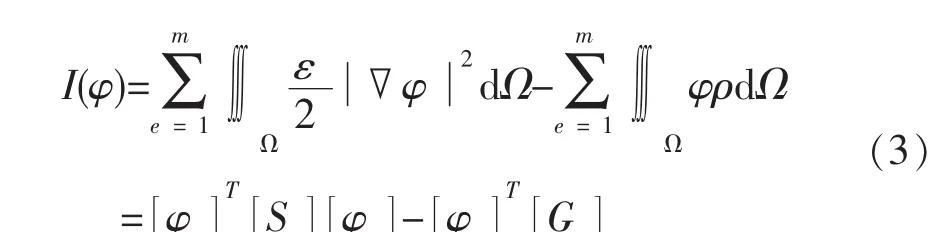
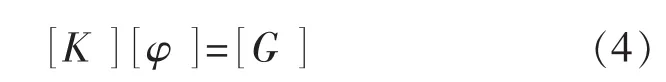
求解式（4），即可得到各节点的电位值φi，进而通过节点电位值，求得单元的电场强度Ei。

根据场致电流密度j的公式：

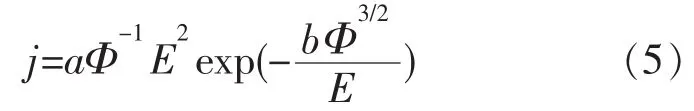
式中：a、b 为常数，a=1.54×10-6（A·eV·V-2），b=6.83×107（V·eV-3/2·cm-1）；Φ 为阴极表面逸出功；E 为电场强度。

当电场强度E低于107V/cm时。

假设电极每个单元节点的蚀除坑形状为半球形，则受尖端作用影响较小的部位，其节点的蚀除坑半径为：

对各节点蚀除凹坑绘制包络面，从而得到加工后的工具电极形状。从图2可看出，在电极的端部与侧壁均存在一定的蚀除现象，而存在尖端放电的电极边缘部位蚀除较明显，沿着加工深度方向，尖端放电的作用逐渐减小，蚀除量也随之逐渐减小，最终趋于稳定。因此，在进行电极损耗补偿时，一般选择稳定阶段电极端面和侧壁的蚀除深度作为电极补偿的补偿量。

图2 电极蚀除包络图

2 基于神经网络的电极损耗计算模型

如果利用电极的几何形状进行电极补偿，就要求系统能实时且准确地反馈加工过程中的电极几何形状，否则，补偿值将无法满足加工需求，导致产生加工误差。然而，电极的几何形状预测计算量较大，目前系统的计算能力仍无法满足实时性要求。同时，由于加工间隙内的情况较复杂，导致电极的损耗是动态的。因此，按工件损耗轮廓对电极进行自动补偿的方法仍较难实现。

神经网络能模拟人脑并行处理模式，具有较强的思维推理、自学习、判断和记忆的能量。因此，本文选择神经网络，通过样本的训练来建立加工工艺参数、加工时间与工具电极轴向、径向损耗量的关系。模型建立过程见图3。

图3 电极损耗模型建立过程

2.1 样本的选择与获取

本文选择峰值电流ie、脉冲宽度td、切削深度ap、电极截面积Se、冲液压力p、加工时间t等6个对电极损耗影响较大的因素作为神经网络的输入参数，对每个因素分别选择4种水平（表1）进行正交试验。其中，峰值电流与脉冲宽度通过示波器对加工间隙实时测量得到，冲液压力通过冲液入口的稳压阀控制得到，加工时间由机床数控系统自动监测记录，其余输入参量都可在实验前对其进行测量设定。实验中，电极材料为石墨，工件材料为SiCp/Al，主轴转速为1000 r/min，开路电压为100 V，并使用接触感知的方法获得电极的轴向损耗值与径向损耗值。本文对每种加工参数都进行多组实验，使用狄克逊准则[5]和极差比的方法，通过比较极差比统计量d0及狄克逊检验临界值dα(n)，来去除其中的坏值，并取剩余数据的平均值作为训练的样本数据。

表1 电弧铣削实验输入参数

2.2 网络训练

本文选用3层前馈式神经网络模型，以峰值电流、脉冲宽度、切削深度、电极截面积、冲液压力、加工时间等6个加工参数作为模型的输入，以电极的轴向损耗值与径向损耗值作为模型的输出，隐含层采用径向基函数（一般取高斯函数）作为激励函数。电弧铣削神经网络预测模型结构见图4。

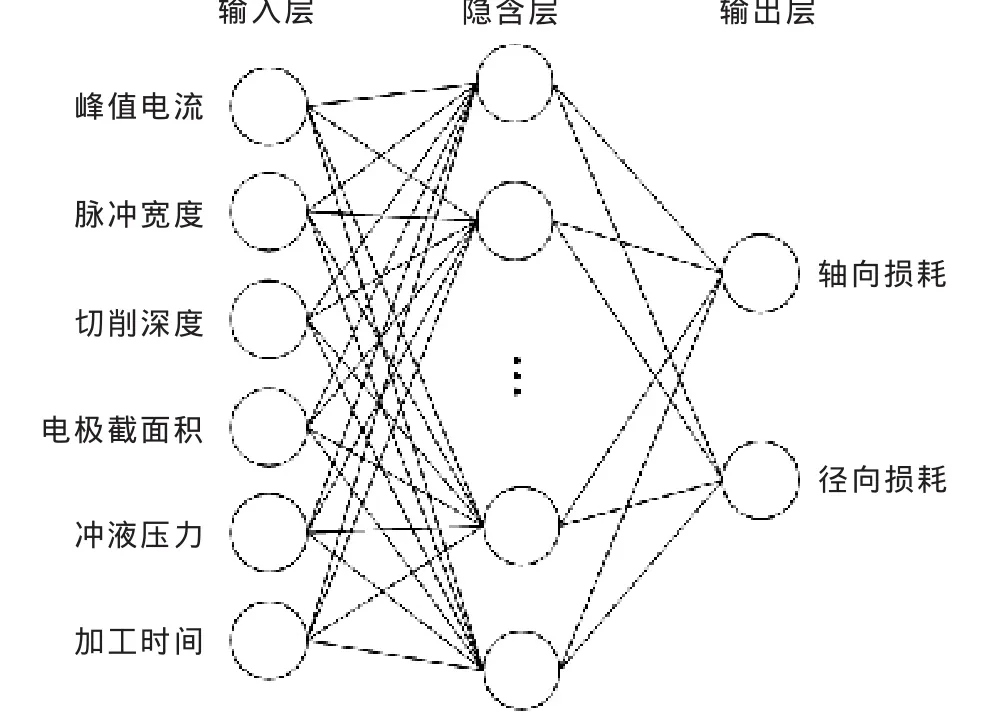
图4 电极损耗神经网络模型结构图

由于广义回归神经网络[6]有较强的逼近与学习能力，在数据缺乏的情况下，也具有较好的收敛效果，故选用其对电极损耗模型进行训练，可在MATLAB中使用式（7）调用：

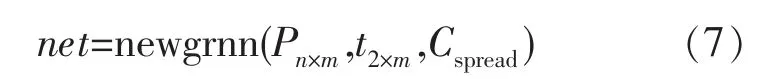
式中：net为返回值；P为输入矩阵；t为输出矩阵；C为光滑因子。

3 电极损耗在线实时补偿策略

在旋转内冲液铣磨加工中，电极损耗不仅与电源输入的能量有关，还与加工间隙的加工状态有关，即：

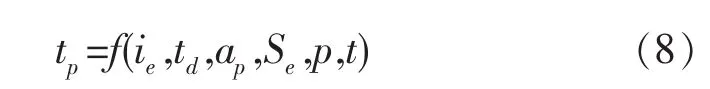
式中：ie为峰值电流；td为脉冲宽度；ap为切削深度；Se为电极截面积；p为冲液压力；t为加工时间。

在完成了电弧铣削电极损耗广义回归神经网络的建模与训练后，就可调用网络仿真函数式（8）来计算加工中电极的轴向与径向的损耗：

式中：net为训练后的电极损耗预测模型；pp为网络输入参数；tp为相应的电极耗损量。

通过广义回归神经网络得到损耗量，在加工中实时地进行连续补偿。目前，数控机床主要使用定长补偿策略[7]，它是一种非连续的电极损耗补偿方法（图5），但其辅助时间较长，且工件的表面轮廓易造成周期性波动。

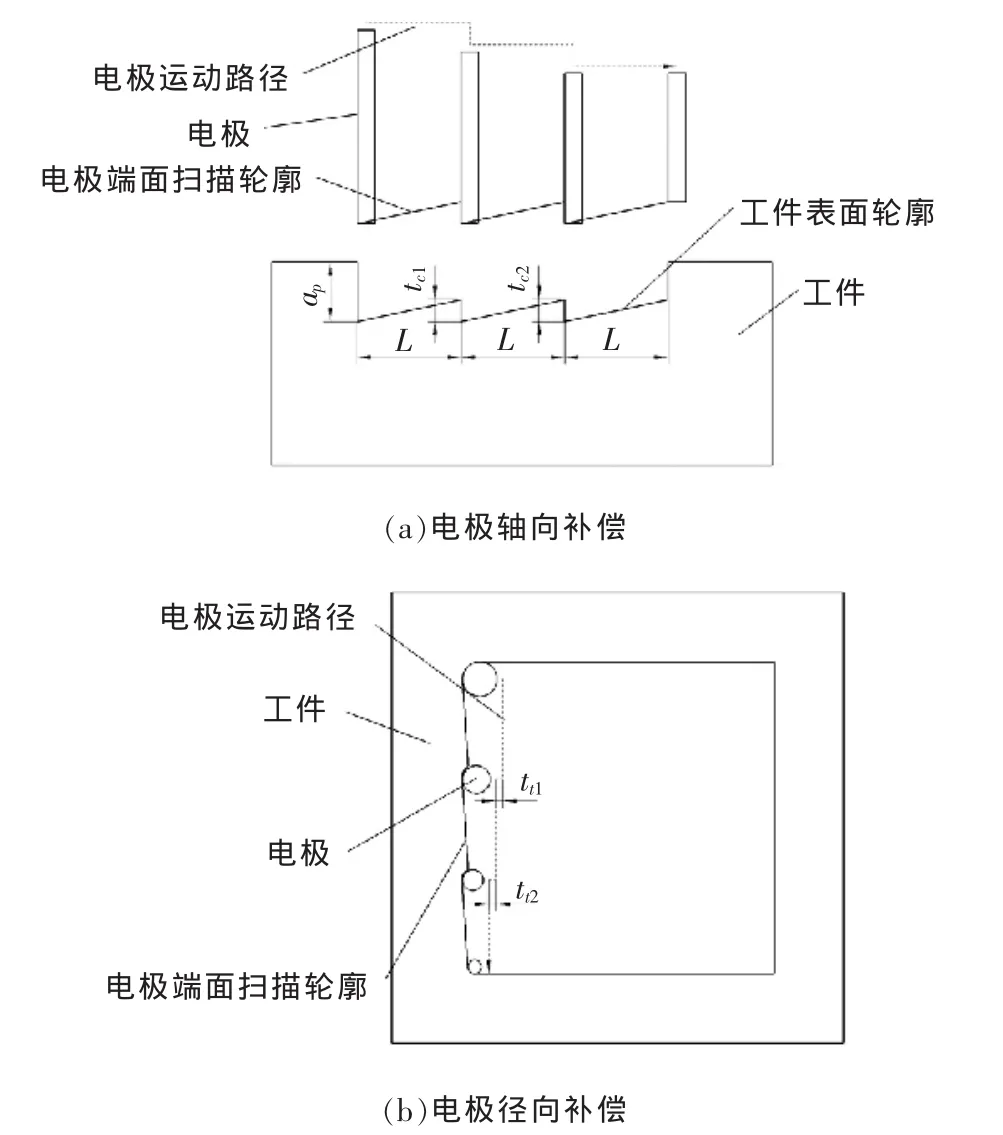
图5 电极损耗定长补偿示意图

针对上述问题，对定长补偿策略进行了改进。改进后的补偿策略并不是在每一次进给周期结束后，将该段时间内的电极轴向与径向的损耗量一次性地进行补偿，而是预先在进给运动周期开始前，根据之前的状态参数进行预测，得到在下一个周期中电极的轴向与径向的损耗量，从而得出所需的Z轴偏移量与电极半径补偿值。在数控系统中，根据该周期内进给运动的脉冲数进行线性插补运算，可得到一个脉冲内电极在轴向与径向的偏移量，从而在工件坐标系内平移一个补偿量。在实际进给运动时，电极是斜向下进给的。需说明的是，该补偿量是由之前周期内的状态参量根据神经网络预测得到的电极损耗量，所以必须保证各进给周期是平滑过渡的，两周期间的电极损耗量要求相近。该补偿策略的示意图见图6。

图6 电极损耗预测补偿示意图

电极损耗预测补偿策略的特点有：

（1）基于广义回归神经网络的电极轴向与径向损耗预测补偿方法，通过对数控系统实时监测电弧铣削的加工状态与加工参数，用神经网络模型进行预测，得到电极轴向与径向的损耗量。检测过程无需中断运动轨迹、回零测量。

（2）通过线性差分的方法，在电极每个运动脉冲内加入补偿量，使电极的损耗补偿连续，从而使加工过程平滑有序地进行，提高了加工效率与工件表面质量。

（3）由于是状态预测补偿，要求相邻两周期的电极损耗量需相近，如果加工状态存在瞬时突变的情况，会造成补偿量产生一定的偏差。

4 实验验证

4.1 实验装置

采用龙门式高速电弧放电加工铣削机床，可进行X、Y、Z方向进给，实现轮廓与型腔的铣削。电极采用多孔石墨电极，安装于旋转冲液机构上。工件采用体积分数为25%的SiCp/Al复合材料，通过加工宽20 mm、深5 mm、长60 mm特征槽的方式，对电极补偿前后的状态进行分析。加工参数见表2，实验装置见图7。

表2 电弧铣削加工参数

图7 电弧铣削加工实验装置

4.2 实验结果分析

对补偿前后的特征槽形貌进行对比，可明显看出，补偿后工件的尺寸精度显著提高。无电极补偿加工的零件，在加工初期，槽口的形态仍满足要求，但随着加工的进行，电极损耗逐渐增大，两槽边呈逐渐收缩减小的趋势（图8a）；有电极补偿加工的零件，两槽边的一致性明显上升，槽口和槽尾的尺寸相差无几（图8b）。

图8 特征槽形貌图

对补偿前后特征槽的末端宽度、末端深度及长度进行测量，数据显示，电极补偿后的测量值均有所提高，与设计要求的加工尺寸偏差均在1 mm以内，在保证一定加工精度的条件下，满足了工件粗加工的基本需求。

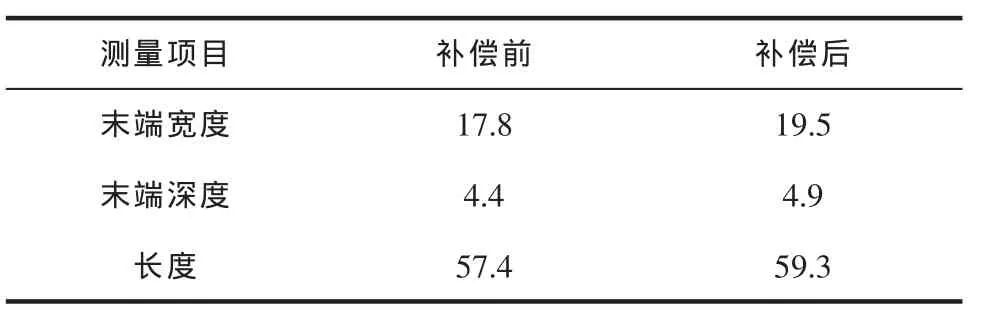
表3 特征槽实测数据

5 结语

本文建立了电弧铣削加工电极的蚀除形状模型，并基于广义回归神经网络，通过对样本的训练与处理，得到了加工参数、间隙状态参量与电极损耗量的映射关系。在定长补偿策略的基础上，提出了电极损耗预测补偿方法，使加工过程能实时连续地进行，既提高了加工效率，也提高了工件的表面质量。

[1] Zhao Wansheng，Gu Lin，Xu Hui，et al.A novel high efficiency electrical erosion process-blasting erosion arc machining[J].Procedia CIRP，2013，6：621-625.

[2] Liu Yonghong，Ji Renjie，Li Xiaopeng，et al.Effect of machining fluid on the process performance of electric discharge milling of insulating Al2O3ceramic[J].International Journal of Machine Tools and Manufacture，2008，48（9）：1030-1035.

[3] 黄河.基于内冲液旋转电极的电火花铣削机床与关键技术研究[D].哈尔滨：哈尔滨工业大学，2010.

[4] 张彦振，刘永红，张锐，等.高速电弧加工材料去除机理研究[C]//第15届全国特种加工学术会议论文集（上）.南京，2013：410-416.

[5] 邱轶兵.试验设计与数据处理[M].合肥：中国科学技术大学出版社，2008.

[6] 孙禹，徐克林，秦玮.基于广义回归神经网络的工程公司风险评估[J].工业工程，2011（3）：119-123.

[7] 裴景玉，邓容，胡德金.微细电火花加工的底面轮廓模型及定长补偿方法 [J].上海交通大学学报，2009（1）：42-46.