一种MIMO雷达谱修正旁瓣抑制方法的研究∗
2015-01-23
(电子科技大学电子工程学院,四川成都611731)
0 引言
多输入多输出(MIMO)雷达[1]发射端采用相互正交的信号,在空间形成宽的低增益发射波束。MIMO雷达较之传统雷达有许多新特性,在目标分辨、低速目标检测、抗截获等方面有很大的优势,成为了当今雷达界的研究热点。针对窄带频分MIMO雷达系统,由于接收机带宽受雷达系统的限制,而MIMO雷达发射频分的正交信号将占用较大的带宽,使得子带信号带宽减少,从而导致信号时带积变小,使得信号具有较大的距离旁瓣,影响弱目标的探测。因此需研究时带积较小时距离旁瓣的抑制算法[2-9],提高频分MIMO雷达系统的检测性能。
文献[7]利用数字滤波便于频谱处理的特点,针对小压缩比线性调频(LFM)信号幅度谱的菲涅尔(Fresnel)波纹对距离旁瓣的突出影响,提出了谱修正抑制旁瓣设计的方法。文献[8]针对小时带积线性调频信号,提出了采用频谱修正方法来提高脉冲压缩信号的主副比。文献[9]提出了倒数谱滤波和对合成信号频域整体加窗的方法,这两种方法本质上也是一种谱修正技术,只是倒数谱滤波仅针对合成前的窄带信号进行,不能有效地减少相邻频带信号间的起伏,而对合成信号频域整体加窗只能有效地平滑频谱的边缘跃变,所以两种方法结合的旁瓣抑制的效果不能达到工程的实际要求。
本文主要从谱修正技术出发,将MIMO雷达接收的信号看成一个整体,作为合信号,然后对它进行谱修正,即对MIMO雷达的综合输出信号(通过匹配滤波和波束形成后的信号)进行频谱修正,将其频谱修正为窗函数的形状,这样使得输出信号的时域旁瓣降低。
1 谱修正技术
对线性调频信号频谱的修正可以通过修改匹配滤波器的传输函数来实现[8]。设线性调频信号的实际频谱为S(f),匹配滤波器的传输函数为R(f),将线性调频信号的频谱修正为矩形,就是使匹配滤波器的输出具有矩形谱。这样只须满足条件:
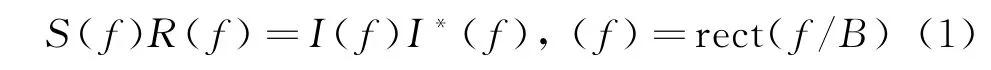
显而易见,修改后匹配滤波器的传输函数为
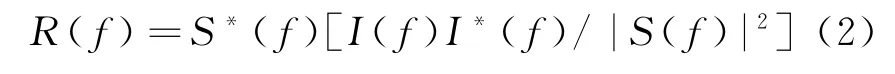
通常加权网络的传输函数W(f)=W(f)·rect(f/B),因此,线性调频信号的频谱修正与加权处理可合二为一,其原理框图如图1所示,其等效的数字处理原理图如图2所示。首先,对线性调频信号s(t)作采样,得采样序列s[n]=s(n Ts),Ts为采样周期,对s[n]实施快速傅里叶变换(FFT),得s(t)的数字谱S[k]。然后,将加权网络的传输函数W(f)转换为数字域形式W[k]。由此,得到数字处理原理图(图2)。其中∗代表卷积运算,IFFT 表示 逆FFT运算。
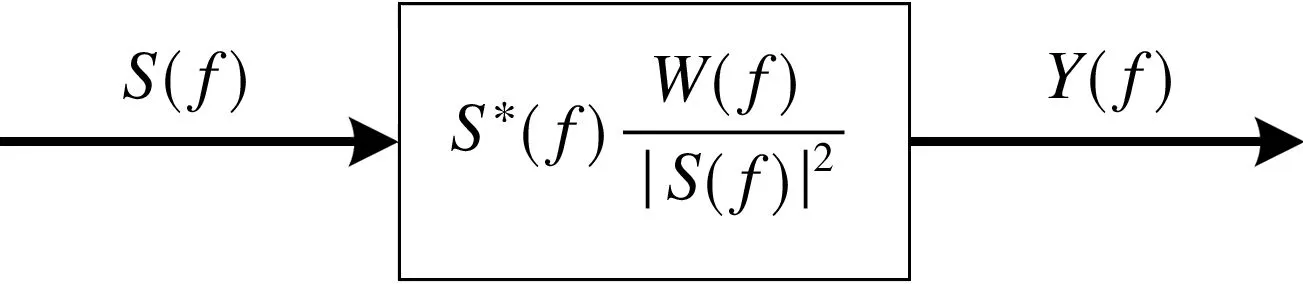
图1 线性调频信号频谱修正
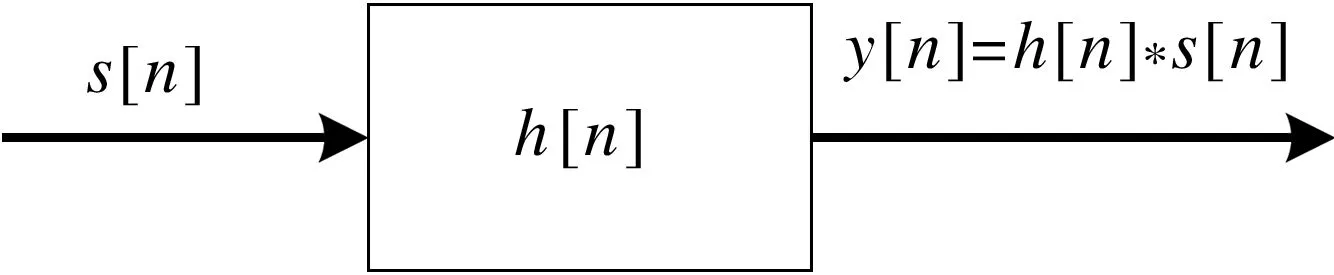
图2 线性调频信号频谱修正的数字处理框图
然而,加权网络的引入实际上是对信号进行失配处理,它不仅使旁瓣受到抑制,同时又使脉冲压缩信号的主瓣降低、展宽。因此,这种旁瓣抑制是以信噪比损失和分辨率变差作为代价的。
2 MIMO雷达中的谱修正方法
对于MIMO雷达,如图3所示,可以对常规的综合处理输出信号(依次对阵列接收信号作接收波束形成、匹配滤波、发射波束形成)进行频谱修正。完成常规处理的综合输出信号可以表示为
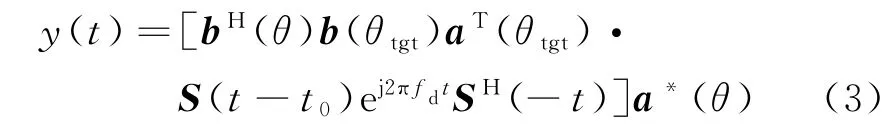
式中,S(t)=[s0(t),s1(t),…,s M-1(t)],M为发射阵元数,S(t)为正交线性步进频信号,t0为回波时延,fd为多普勒频率,a(θtgt)为发射导向矢量,b(θtgt)为接收导向矢量,b(θ)为接收波束形成矢量,a(θ)为发射波束形成矢量。若速度和目标距离都为0,那么上式等价为
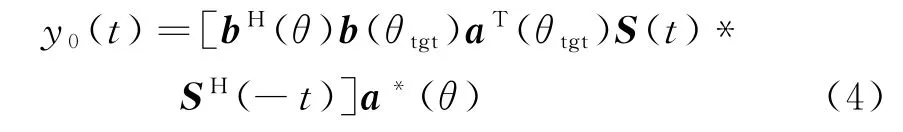
令 该 信 号 的 频 谱 为Y0(ω),H1(ω)=则谱修正滤波器的频谱为
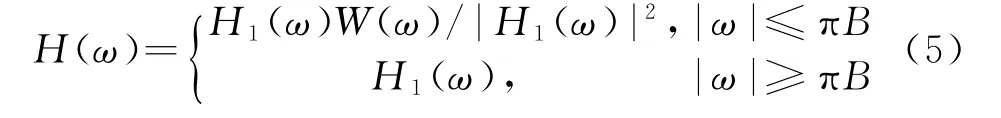
式中,W(ω)为窗函数,B为Y0(ω)的带宽。
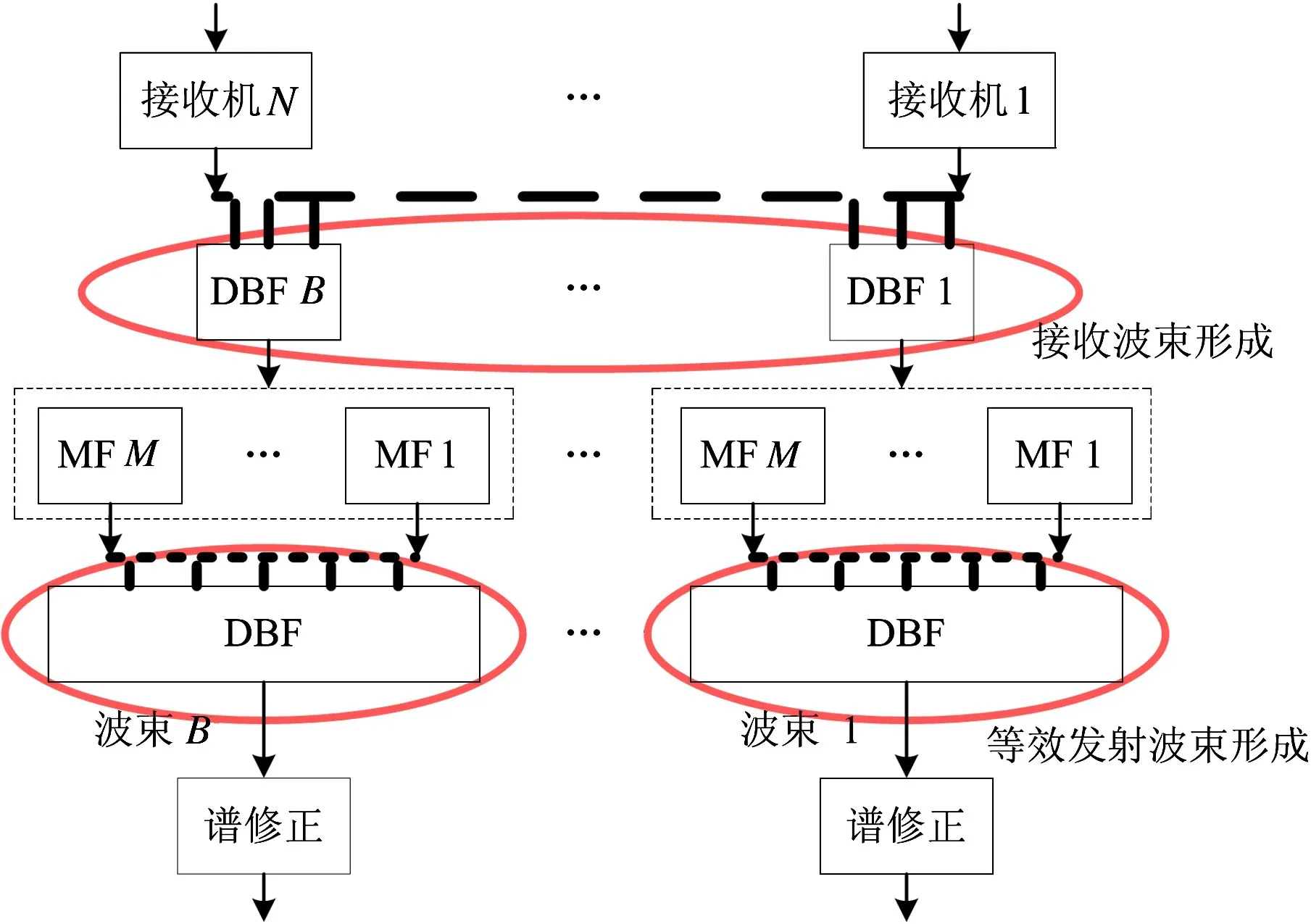
图3 MIMO雷达的回波信号频谱修正处理框图
假设阵列接收到的信号通过综合处理后的y(t)频谱为Y(ω),且由信号与系统的知识可知,,那么这种谱修正
方式输出的信号谱为
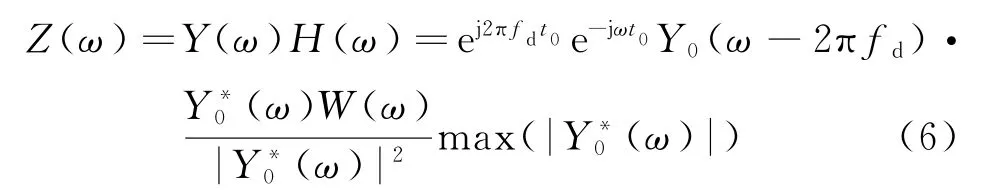
若fd,t0均为0,则上式为
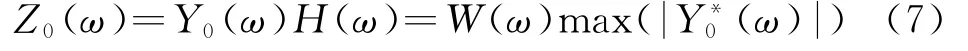
因此,谱修正后的输出信号z0(t)主要受窗函数的影响。
3 实验验证
3.1 计算机仿真验证
为了验证上述方法的正确性,进行了相应的算法仿真。首先用理论MIMO信号进行仿真,收发阵元个数为8,阵元间距为半波长,发射正交线性步进频信号,采样率fs=50 M Hz,周期T=400μs,子带带宽B=1 M Hz,脉宽Tp=4μs,信噪比SNR=10 dB,目标位于距离R=1 015 m,窗函数为Hamming窗。
从图4(a)可以看出,对MIMO雷达的综合输出信号进行谱修正处理后,其输出信号的旁瓣比修正前有明显下降,其旁瓣峰值可达到-40 d B以下。图4(b)给出了线性步进频信号MIMO雷达综合处理输出和谱修正输出后的频谱图,从该图可以看到谱修正处理后输出信号的频谱图就是窗函数的形状,跟理论分析一致,所以时域旁瓣能达到-40 dB以下。
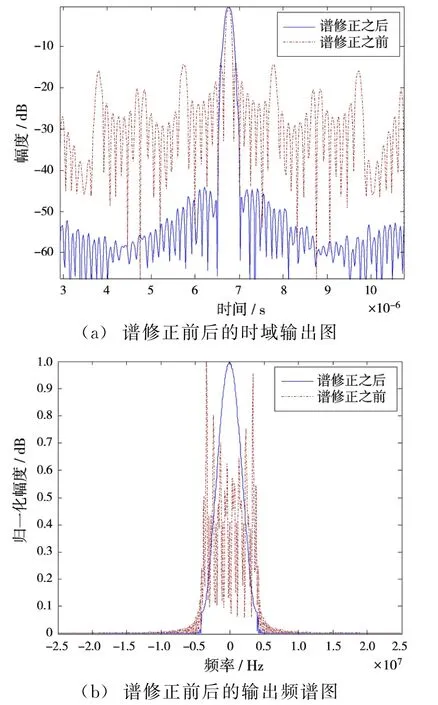
图4 谱修正前后的对比图
在距离R=1 370 m处加一个弱目标,信号强度为R=1 015 m处目标的0.1倍,从图5可以看出,在作谱修正之前,弱目标被强目标的旁瓣所覆盖,从而检测不到弱目标。谱修正之后旁瓣基本在-40 d B以下,所以能检测出弱目标的存在。
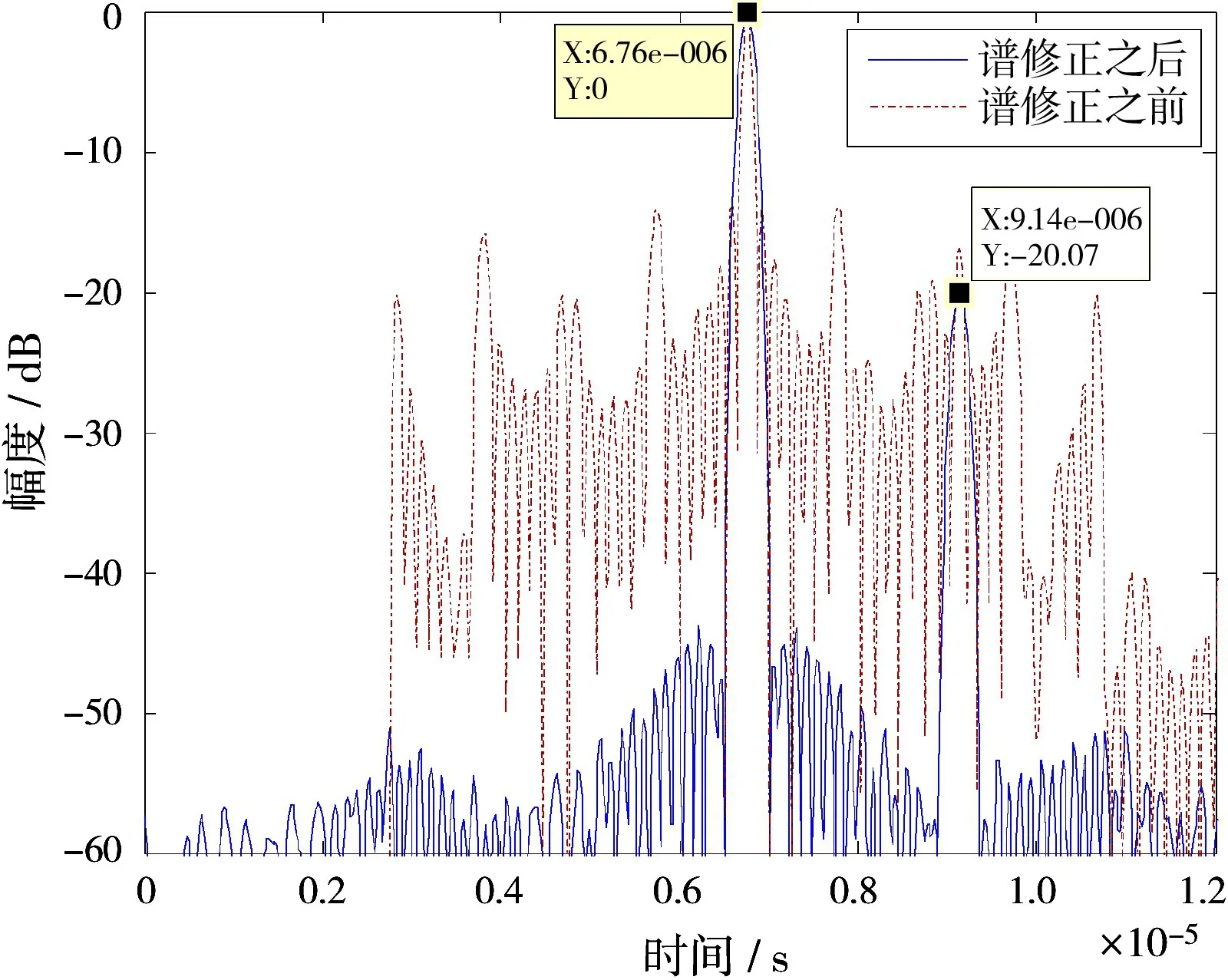
图5 强弱目标谱修正前后的时域输出图
3.2 实测数据验证
实验环境1:发射阵列与接收阵列距离约为200 m,发射阵元数为1,接收阵元数为1,发射阵列法线与接收阵列法线夹角为0°。发射阵列发送线性调频信号,中频信号的频率为60 MHz,中频采样率fs=50 M Hz,周期T=400μs,带宽B=1 MHz,脉宽Tp=4μs。对接收天线收到的信号作谱修正,得到如图6所示的结果。
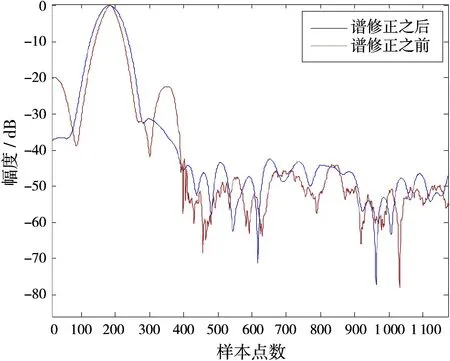
图6 单阵元实测数据谱修正前后的时域输出图
从图6可以看出,谱修正之前最大旁瓣达到了-22.33 d B,而进行谱修正处理之后,旁瓣降到了-35 dB以下。但是谱修正处理使主瓣展宽了,对目标的距离分辨率降低了,与理论分析一致。
实验环境2:发射阵列与接收阵列距离约为200 m,发射阵元数为7,接收阵元数为1,发射阵列法线与接收阵列法线夹角为0°。发射阵列发送线性步进频信号,中频信号的频率为60 MHz,中频采样率fs=50 M Hz,周期T=400μs,子带带宽B=1 MHz,脉宽Tp=4μs。对接收天线收到的信号作谱修正,得到如图7所示的结果。
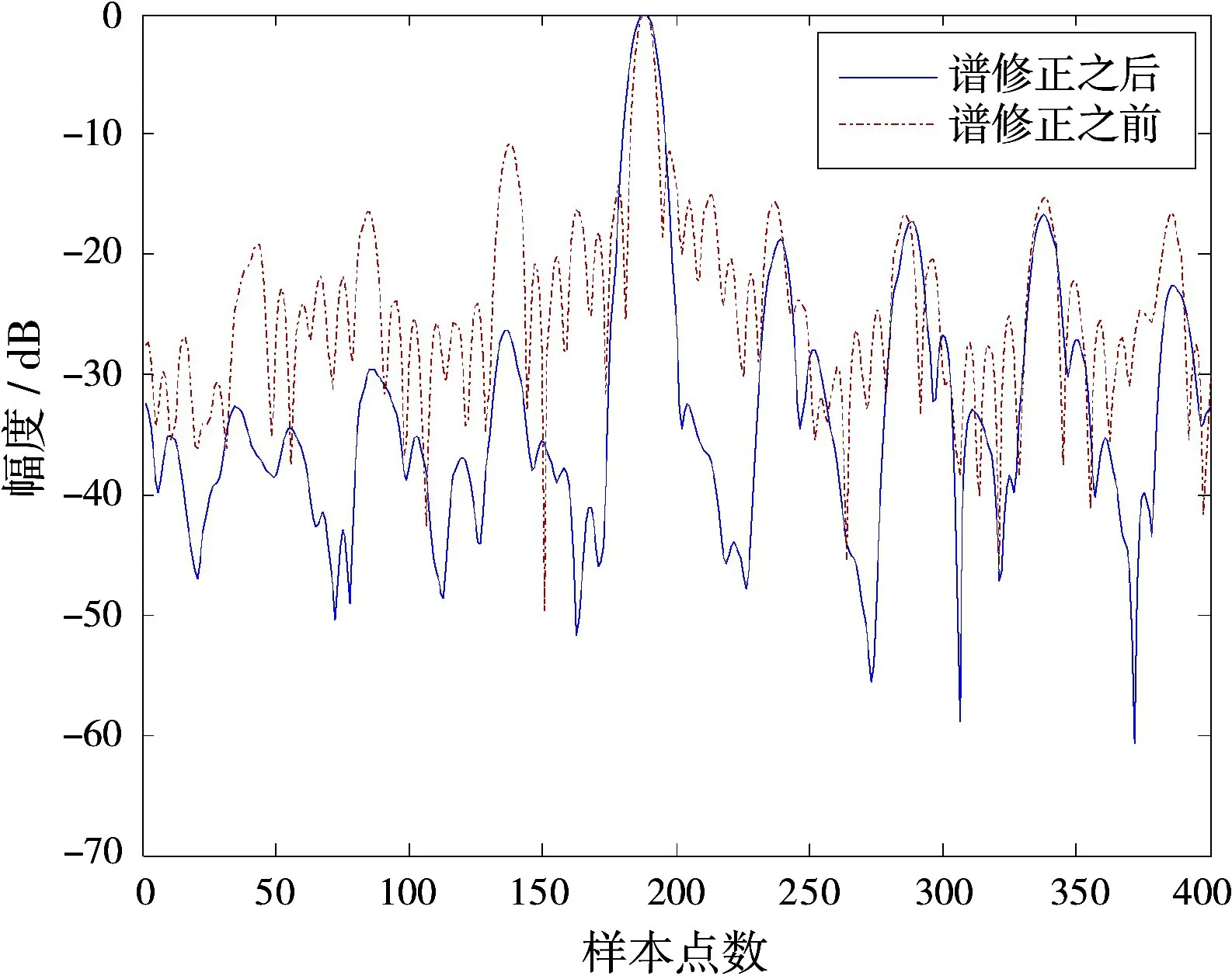
图7 MIMO雷达实测数据谱修正前后的时域输出图
从图7可以看出,MIMO雷达谱修正之前最大旁瓣达到了-10 dB左右,而进行谱修正处理之后,最大旁瓣被抑制到-30 dB左右,由于实际系统产生的信号与理论信号存在一定的差异,使得修正后频谱不是理想的矩形谱,得到的结果不如理论分析理想,但是谱修正还是在一定程度上抑制了旁瓣电平。
4 结束语
本文提出了将MIMO雷达的综合处理输出信号进行谱修正处理的方法,使用这种谱修正技术能有效地抑制MIMO雷达中的距离旁瓣。计算机仿真和实际MIMO雷达阵列数据的处理证明,通过这种方法将MIMO雷达输出信号的频谱修正为窗函数的形状,能取得很好的主副比,且合成信号频域加窗输出信号的主瓣宽度与窗主瓣宽度一致,所以会带来一定的信噪比损失。
[1]LI J,STOICA P.MIMO Radar with Collocated Antennas[J].IEEE Signal Processing Magazine,2007,24(5):106-114.
[2]尹彩玲,罗丰,高媛媛,等.S型非线性调频信号的谱修正脉压研究[J].雷达科学与技术,2008,6(2):134-137.YIN Cai-ling,LUO Feng,GAO Yuan-yuan,et al.Research on Spectra Modified Pulse Compression of S-Mode Nonlinear Frequency Modulated Signal[J].Radar Science and Technology,2008,6(2):134-137.(in Chinese)
[3]张云雷,龚诚,卢建斌,等.一种基于谱修正数字脉压旁瓣抑制的改进方法[J].舰船电子工程,2013,33(2):61-63.
[4]邹彬彬,陈晶晶,荆成财,等.谱修正技术在脉冲压缩信号检测中的应用[J].声学技术,2014,33(3):275-279.
[5]侯东阳,张书毕,万亚豪,等.基于谱修正迭代的Bursa模型[J].海洋测绘,2011,31(5):15-17.
[6]黄德伦,史经捡,廉琦,等.基于法方程病态的谱修正迭代算法的探讨[J].测绘科学,2013,38(2):35-37.
[7]POWELL T H,SINSKY A I.A Time Sidelobe Reduction Technique for Small Time-Bandwidth Chirp[J].IEEE Trans on AES,1974,10(5):112-116.
[8]吕幼新,向敬成,陈辅新.降低线性调频脉冲压缩信号旁瓣的方法[J].电子科技大学学报,1993,22(4):344-349.
[9]戴喜增.MIMO雷达分集检测和带宽合成的理论与方法研究[D].北京:清华大学,2008.
