双基地MIMO雷达最优化搜索参数设计研究∗

王得旺,刘红明,杨建红,陈克微

(1.兰州大学物理科学与技术学院,甘肃兰州730000;2.电子科技大学电子工程学院,四川成都611731;3.空军试验训练基地,甘肃兰州732750)

0 引言

雷达系统设计中,天线扫描空间安排、波位设计和资源调度是非常重要的,关系到雷达系统最佳潜力的发挥。波束安排和信号形式要根据雷达的工作模式和战术要求,结合波束扫描和波束空间分布特点,使雷达能量资源发挥到最佳状态,同时满足搜索数据率和波束覆盖范围的双重要求[1-4]。

现有关于搜索最优化资源管理的理论主要倾向于在一定探测性能约束下最优化雷达资源使用或者资源受限的情况下最优化雷达探测性能[5-8]。双基地MIMO雷达(Bistatic MIMO Radar),发射阵列子阵发射彼此正交的信号,在空间形成宽波束,具有监视范围广、防低空突袭、反隐身等突出优点,近年来受到人们的广泛关注[9]。文献[10]建立了MIMO雷达搜索模式下的射频隐身性能模型,文献[11]利用搜索模式SFDLFM信号的“距离-角度”耦合效应,提出了改善匹配滤波输出损失的搜索单元划分方式。但以上研究针对的是相控阵雷达以及MIMO雷达搜索优化或者双基地MIMO雷达搜索划分,没有专门研究双基地MIMO雷达搜索模式下的资源管理问题。本文建立了双基地MIMO雷达搜索优化的模型和基本设计思路,为进一步自适应的搜索优化逻辑提供依据。

1 双基地MIMO雷达搜索特性的描述

双基地MIMO雷达发射采用较宽的波束,便于实现对搜索区域的快速覆盖,但是由于其波束增益减小,能量不能充分利用,通过改变接收阵列调度基本子阵的波束指向,在保证对空域所有范围内目标检测能力的基础上,以最短的时间完成对发射波束的覆盖。因此,可以等效地看成是接收采用较窄且具有较高增益的波束,扫描覆盖发射波束,则扫描的数据率由接收阵列决定(假设搜索空域与接收子阵波束指向完全一致)。同时由于接收和发射天线阵列的有效工作范围都是非常有限的,只有发射波束和接收波束相交重叠的有效区域才能被探测到。考虑到对于一般的目标最大飞行高度(20 km)相比目标水平距离(几十乃至数百公里)而言往往是比较小的,因此计算搜索空域的范围时,可以先在一维平面上进行,以减少运算量[11]。搜索范围和接收波束安排计算原理示意图如图1所示。

由图1可以看出,搜索覆盖区域可以是一个四边形区域,也可以是包含椭圆圆边的多边形区域。

2 双基地MIMO雷达搜索覆盖设计

2.1 搜索波束覆盖的基本准则

数字阵列雷达搜索目标时,要对搜索空域立体角进行扫描并形成目标检测报告。一方面,为提高对搜索空域中目标的检测概率,阵列天线波束跃度不宜过大,以减小天线波束形状调制损失。另一方面,为了提高搜索数据率,天线波束跃度又不能太小,波位排列过密还会增加雷达的冗余检测,导致在目标航迹相关、滤波预测等方面数据处理负担增加。因此,数字阵列的最佳波位编排,实际上就是在雷达检测性能损失和搜索数据率之间寻求折衷,在一定的移相器位数条件下,使波束既不存在太多的重叠覆盖(搜索数据率损失),又不存在太多间隙(检测性能损失)[1]。

不论是MIMO雷达还是相控阵雷达,波束扫描都是通过控制数字移相器的相位,使得各个阵元之间形成了固定相位差,所辐射的电磁波就相对于阵列形成指向(惠更斯原理),从而进行有效的搜索任务[4]。

以均匀排列的一维阵列为例,假设阵列间距为d,阵元数为N,波长为λ,数字移相器的位数为q(正整数),其对应的最小相移值为

第k个波束的指向θk为

由此可以得到相邻波束间的波位跃度:

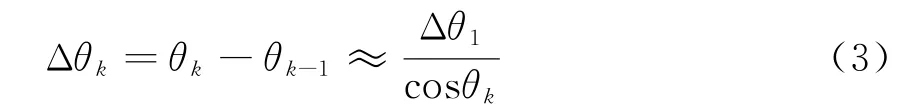
为了更好地衡量波束编排的效率,采用相邻波束的相交电平κ来衡量。令指向θk对应的κ功率点宽度为ϑk,θk-1对应的κ功率点宽度为ϑk-1,如图2所示。

满足:

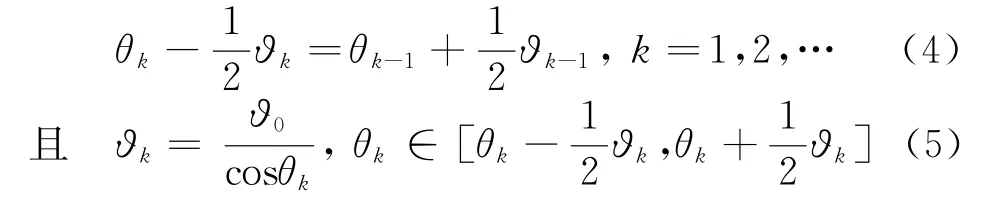
其中,ϑ0为法线方向对应的κ功率点宽度。

则相邻两个波束之间的重叠度定义为

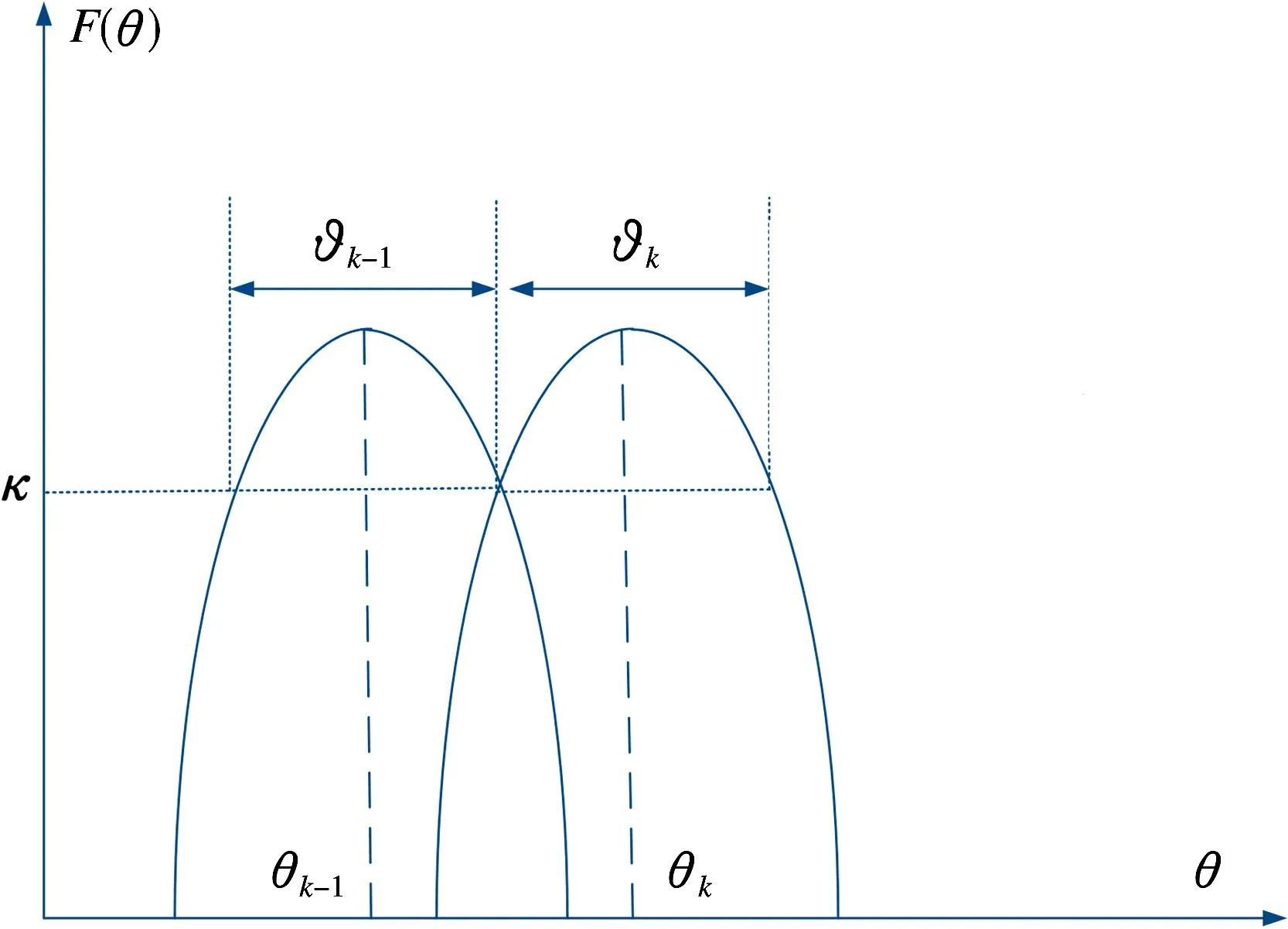
图2 波束覆盖相交电平衡量示意图

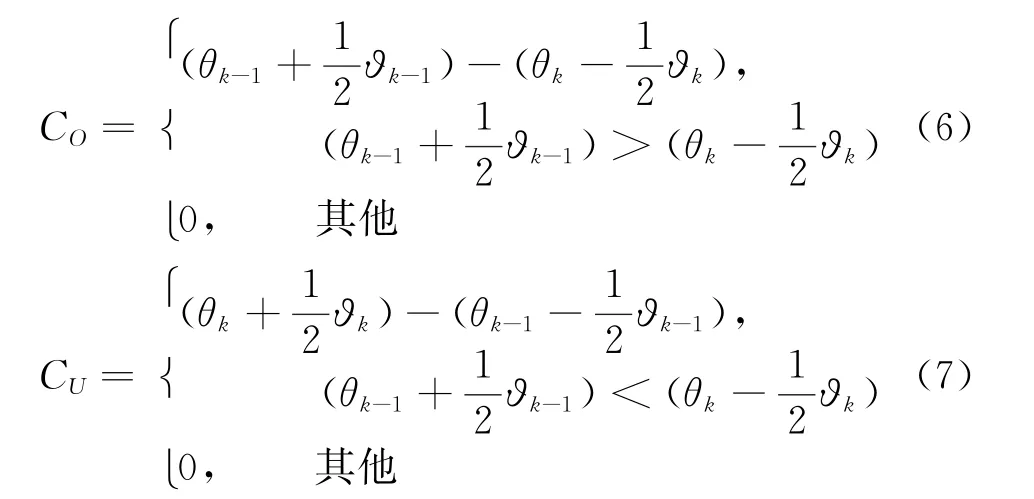
式中,CO代表两波束之间存在过覆盖,重叠度较高,相交电平高于期望值κ;CU代表两波束之间存在欠覆盖,重叠度较低,相交电平低于期望值κ。对于整个阵列扫描范围Ω=θmax-θmin,对应波位数为

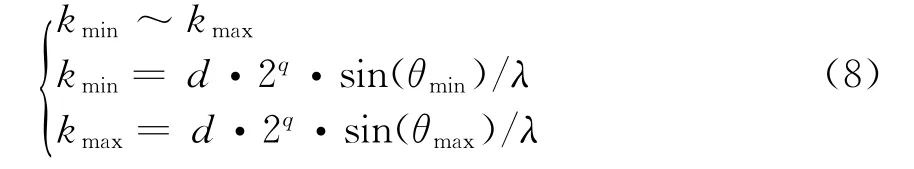
则阵列波束重叠度为

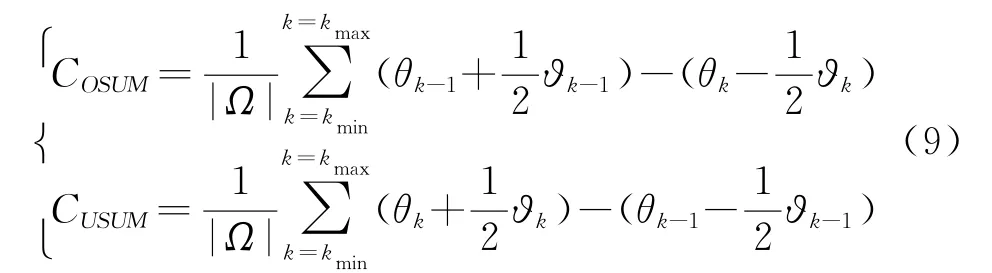
以上是建立在基于波束重叠度几何模型之上波束覆盖损失的分析,更为严格地衡量波束覆盖的效率,应该结合方向图调制损失,将其转化为等效波束间隔(κ功率点宽度与波位跃度的比值)的函数关系,如图3和图4所示。

由图3和图4可以看出 ,随着等效波束间隔的增大,要求覆盖搜索空域的波束数目减少,搜索帧时间相应减少,使得一定帧时间雷达功率消耗降低 ,在达到一个最小值以后,波束间隔增大,波形损耗增加及平均增益降低,造成平均功率消耗又逐渐增大。若主要考虑能量消耗,平均功率最小值点就是最佳的;若主要考虑时间资源 ,则波束间隔应增大。因此考虑搜索覆盖的设计原则时,应该根据资源消耗的需求来选择相应的波束重叠度或者相交电平值。

图3 搜索消耗平均功率与有效波束间隔的关系图

图4 搜索消耗时间与有效波束间隔的关系图

2.2 双基地MIMO雷达波束覆盖设计方法

2.2.1 双基地MIMO雷达的波束编排方法

双基地MIMO雷达接收时,单个接收波束可以保持较高的增益和测量精度及方向分辨率,因此对于任意的发射波束,采用扫描波束对发射波束方位和俯仰覆盖的方法,形成空间交汇区,从而实现对交汇区目标的扫描检测。先由最大距离积算出接收波束搜索的方位和俯仰范围,然后按照波束宽度步进的方式进行波束编排,如图5所示。

图5中角1、角2分别为发射波束对应的方位角θt和俯仰角φt,角3、角4分别为接收波束的方位角θr和俯仰角φr。根据基本关系图可以得出如下关系:

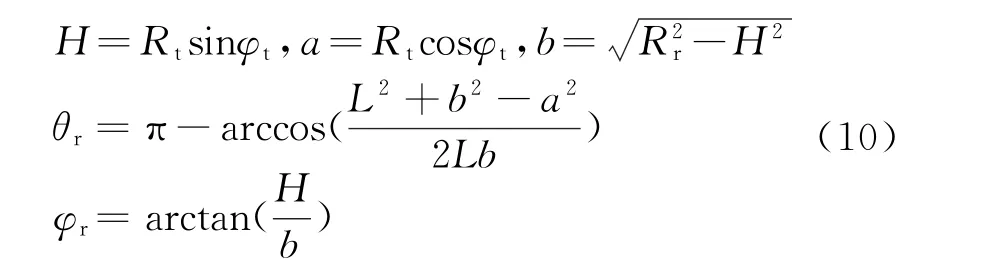
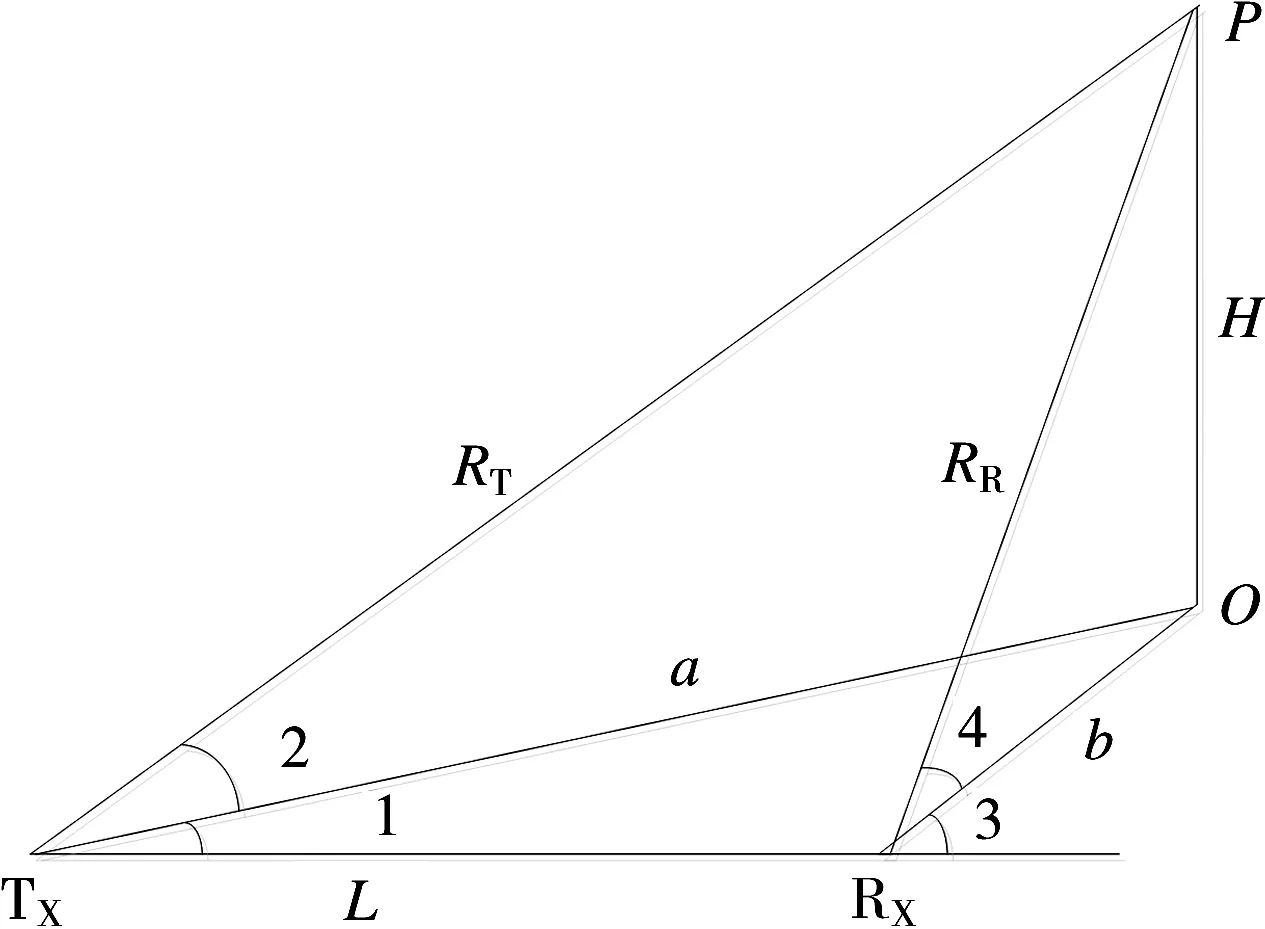
图5 双基地波束编排基本关系图

因此对于特定发射方位和俯仰波束,接收阵列波束覆盖的数目:

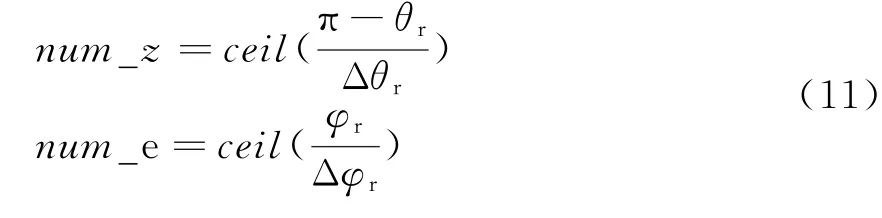
2.2.2 双基地MIMO雷达的优化波束编排思路

双基地雷达接收站接收目标回波时,近距离回波功率较大,利用接收波束用3 dB的波束宽度覆盖整个发射波束,雷达功率得不到充分利用。所以接收波束可以采取在近区用6 dB(或者其他非3 dB值)的波束宽度去覆盖,而远区采用3 dB的波束宽度覆盖的方式,这样减少了搜索多波束的数目,优化波束编排方案。

2.2.3 仿真对比

双基地MIMO雷达接收阵列属于大型面阵,搜索过程中波束宽度比较窄,假设方位维3 dB宽度为2°,俯仰维3 d B宽度为1.5°。根据2.1节分析,主要考虑时间资源消耗时,选取较大的有效波束间隔,选取其值范围为1～1.8。当发射俯仰角为30°,双基地基线长度为30 km时,接收方位维覆盖波束情况如图6所示。

图6 发射俯仰指向30°时的接收波束方位覆盖数目

根据距离和的不同,自适应地选取相应的波束宽度和波束重叠度,进行有效匹配,实现波束数目的优化,结果如图7所示。

图7 发射俯仰指向30°时的接收波束方位优化覆盖数目

通过优化覆盖波束数目,在一定的程度上可以减小搜索资源的消耗,充分利用雷达的功率,合理分配空间能量分布,达到优化搜索的目的。

3 双基地MIMO雷达优化搜索设计

3.1 双基地MIMO雷达优化搜索参数选取

根据双基地MIMO雷达方程易得

式中,Pt为雷达峰值发射功率,Gt为雷达发射天线增益,Gr为雷达接收天线增益,λ为信号波长,σ为目标的RCS,T B为发射波束驻留时间,k为波耳兹曼常数,T0为雷达接收机温度,Lt为系统损耗。又因为

式中,η为占空比,Ts为发射信号脉冲宽度,Np为脉冲重复个数。则

对于固定指向发射波束,接收波束扫描的过程中,不同的接收距离采用不同的波束宽度,因而使得对应波束的接收增益不一样,从而引起的回波信噪比存在差异,进一步利用接收天线增益的关系式:

式中,εR为阵列天线的效率,ψ为对应的波束宽度。当已知信噪比、脉冲宽度、脉冲重复个数、法线方向波束宽度分别为SNR0,Ts0,Np0,ψ0,时:

再将二者相除可得

双基地MIMO雷达搜索性能由跟踪起始距离描述,跟踪起始距离定义为对于给定目标当雷达积累检测概率达到一定值时的距离。对于服从Swerling I起伏特性的目标,雷达单次探测时的检测概率满足:

对于SwerlingⅢ起伏特性的目标,雷达每次探测时的检测概率满足:

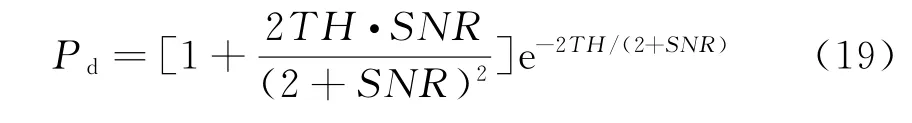
式中,TH代表接收机的检测门限,由虚警概率Pfa确定,SNR代表回波信噪比。

假设双基地MIMO雷达最大接收处理量程为Rs,目标向接收阵列方向径向运动,速度为v,在搜索周期为T f的条件下,一个搜索周期的时间内飞过的距离为ΔR=v T f。若目标第一次被雷达照射时所处的距离为Rs′,那么目标飞至距离R处的积累检测概率为

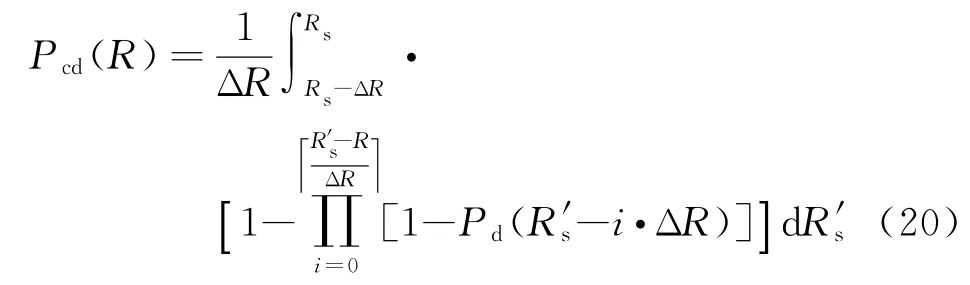
当给定搜索的跟踪起始距离要求时,假定系统要求的跟踪起始距离为Rd,即满足:

式中,Pcdth为积累检测概率的门限。

另外,除上述约束条件外,搜索帧周期及脉冲重复个数还应该满足如下时间资源约束条件:

式中,N B为搜索覆盖波束数目(根据上一节优化覆盖可知),Tp为脉冲重复周期。

搜索任务消耗的资源量包括两个部分:时间资源消耗量和能量资源消耗量。其中,时间资源消耗量(搜索时间负载)可表示为

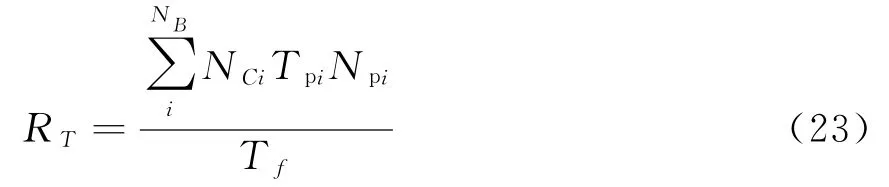
在一定搜索周期T f时间内,系统能量资源消耗量为

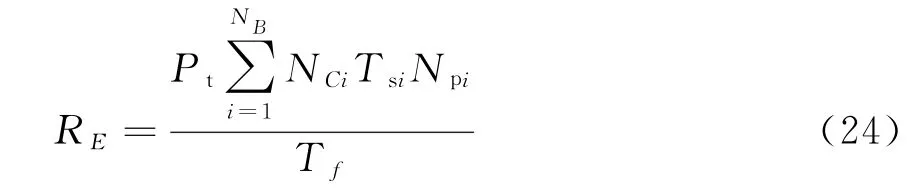
因此,综合时间和能量资源消耗量,搜索任务所消耗的系统资源量可表示为

式中,C1和C2为两个设定的加权系数,满足C1+C2=1,它们的取值反映了用于对系统时间和能量资源消耗量的关注程度。

根据上述分析,可建立如下的搜索任务最优参数分配模型:

其中,目标函数为最小化搜索任务消耗的系统资源,约束条件依次为跟踪起始距离约束、时间约束。上述优化模型所确定的最佳搜索执行参数使得搜索任务所消耗的系统资源极小化,使得更多的剩余资源可用于执行目标跟踪、识别等其他任务。

当可选参数的可能取值为有限个数时,假设T f具有M个可能的取值,Ts具有P个可能的取值,Np具有Q个可能的取值,此时可采用简单的搜索策略求解优化问题,步骤如下:

Step1 根据T f,Ts和Np的可能取值,形成M×P×Q个(T f,Ts,Np)组合;

Step2 对应于各个组合,按照式(20)计算在给定跟踪起始距离处的积累检测概率,并判断是否满足要求的积累检测概率门限,选出满足门限要求的M1个组合;

Step3 根据优化覆盖计算搜索所需的波位数,并对上述M1个组合分别判断是否满足式(26)所示的第二个约束条件,选取满足该约束条件的组合,假设共有M2个组合;

Step4 将上述M2个组合代入式(26)所示的目标函数中,选择使得其获得极小值的参数组合作为最终选取的最佳执行参数。

3.2 仿真结果

根据双基地MIMO雷达系统设计的需求,设定仿真参数如表1所示。

表1 双基地MIMO雷达系统仿真参数

如图8所示,随着积累检测概率门限的增大,检测性能要求提高,为了达到需要的积累检测概率门限,此时目标飞至跟踪起始距离处的积累次数必须增大,因此所选取的最佳搜索帧周期随之减小。若仅关注系统消耗的时间资源应选取最小Np/T f对应的参数组合,若仅关注系统消耗的能量资源选取最小TsNp/T f对应的参数组合。若同时关注系统消耗的时间和能量资源,则受到3个参数的联合制约。所以,随着检测门限值的增大,搜索周期整体上呈下降趋势,但曲线波动受到脉冲重复个数和脉冲宽度的影响。

图8 最佳搜索周期随检测概率门限值的关系图

随着检测门限值的增大,所需要的回波信噪比增大,在对应波束位置上的驻留时间增大,即在脉冲重复周期固定的前提下,增大脉冲重复个数。然而,如图9所示,在检测概率门限值为0.92,0.94,0.96,0.98处呈波动下降态势,这是因为选取最优资源消耗时,脉冲宽度的选取与脉冲重复个数的选取相互制约。在图10中脉冲宽度基本维持在500μs(占空比为0.25)的水平,但也在检测概率门限值为0.92,0.94,0.96,0.98处呈波动上升态势,所以二者维持了平衡,使得资源最优化选取合理。

图9 最佳脉冲重复个数随检测概率门限值的关系图

图10 最佳脉冲宽度随检测概率门限值的关系图

如图11所示,在一定的搜索周期里,搜索所消耗的时间资源所占比值保持在0.02～0.07之间,整体上随着检测概率门限值的增大,也在门限值为0.92,0.94,0.96,0.98处呈波动下降态势,这是由于这些点处驻留时间减小的缘故。如图12所示,搜索所消耗的能量资源则完全呈递增趋势,原因在于搜索探测中资源消耗一直存在,且是熵值不断增大的过程。通过分析以上参数规律对资源消耗的影响,在设计最优化搜索逻辑过程中确定大致的参数范围,从而有效地减少资源浪费,使得雷达系统能高效地处理搜索,以及确认、跟踪等其他任务。

图11 最优化时间资源负载随检测概率门限值的关系图

图12 最优化能量资源随检测概率门限值的关系图

4 结束语

本文针对双基地MIMO雷达搜索特性,从波束覆盖的几何模型出发,分析搜索过程中波束覆盖的基本准则,并在此基础上提出了双基地MIMO雷达搜索波束覆盖优化的基本思路。最后建立了在约束条件限制下,同时考虑时间资源和能量资源的搜索模型,仿真分析了影响搜索资源消耗参数最优值随检测概率门限值的变化规律,以及各参数之间的相互制约对资源消耗的影响,为搜索优化的参数选取提供依据,同时为进一步实现双基地MIMO雷达自适应的优化搜索提供基本框架支撑。

[1]王雪松,汪连栋,肖顺平,等.相控阵雷达天线最佳波位研究[J].电子学报,2003,31(6):805-808.

[2]张华睿,杨宏文,郁文贤.相控阵雷达最优搜索参数设计研究[J].兵工学报,2012,33(9):1062-1065.

[3]李文臣,刘付兵,袁翔宇,等.地基相控阵雷达的天线扫描空间分析[J].雷达科学与技术,2004,2(5):309-314.

[4]李秋生,谢晓春,刘小燕.相控阵雷达功耗约束分区优化搜索方法[J].制导与引信,2013,34(2):29-33.

[5]BILLMAN E R.Parameter Optimization in Phased Array Radar[C]∥IEE International Conference on Radar,Brighton,UK:[s.n.],1992:163-168.

[6]BILLMAN E R.Design and Performance Considerations in Modern Phased Array Radar[C]∥IEE International Conference on Radar,London,UK:[s.n.],1982:15-19.

[7]孙涛,山秀明,陈鲸.空间监视相控阵雷达匹配搜索技术研究[J].系统工程与电子技术,2013,35(6):1183-1187.

[8]邓桂福,刘华林,胥雷.远程相控阵雷达搜索参数优化设计[J].雷达科学与技术,2012,10(1):32-36.

[9]刘红明.双基地MIMO雷达原理与理论研究[D].成都:电子科技大学,2010.

[10]杨少委,程婷,何子述.MIMO雷达搜索模式下的射频隐身算法[J].电子与信息学报,2014,36(5):1017-1022.

[11]段翔,刘周,刘红明,等.双基地 MIMO雷达搜索处理方法研究[J].信号处理,2013,29(3):319-325.