PD 雷达导引头海杂波回波信号模拟

(中国人民解放军92941部队93分队,辽宁葫芦岛125001)

0 引言

雷达系统模拟的核心是建立雷达目标回波信号及各种杂波信号散射、传播特性的模型,从而对雷达的性能和指标进行评估和测试。杂波的散射特性直接影响雷达对目标的检测和跟踪性能,例如杂波的功率谱特性与雷达的运动目标显示及空时自适应信号处理(STAP)滤波器的设计密切相关,杂波的幅度统计特性是雷达恒虚警检测器设计的重要依据[1-2]。对于弹载雷达导引头来说,面临一个很重要的背景环境——海杂波。

目前对海杂波的建模主要集中在物理散射机理建模和统计特性建模上。物理散射机理建模主要研究电磁波与海面的相互作用以及海面杂波单元的散射机理,能够从本质上对杂波散射特性进行解释,缺点是模型复杂,计算量大,不易形成快速算法。统计特性建模建立在大量的实测数据的基础之上,是一种经验模型[3]。杂波仿真的实质是产生服从特定概率密度分布的相关序列,常用的方法有零记忆非线性法(ZMNL)和球不变的随机过程法(SIRP)。

本文结合反舰导弹不同的作战背景,提出了一种基于K分布的海杂波回波信号模拟的方法。首先采用SIRP法对海杂波的幅度分布进行建模,功率谱模型采用高斯谱,然后将产生的K分布杂波序列叠加到PD雷达的发射波形中,合成海杂波的回波信号,最后给出了仿真结果和实验分析。

1 PD雷达导引头海杂波信号建模

1.1 海杂波回波信号的数学模型

常用的PD雷达导引头发射信号有线性调频信号,相参脉冲串信号以及二进制相位编码信号。本文采用的是线性调频信号,它的时域表达式为

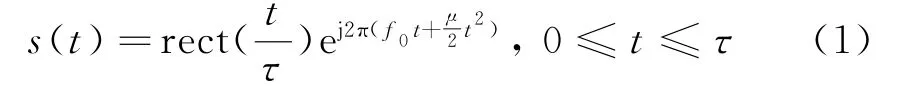
式中,f0为发射信号中心频率,表示脉宽为τ的矩形脉冲函数,μ为线性调频系数,其值为μ=B/τ。

雷达回波信号产生的实质是雷达的发射信号作用于目标并发生后向散射,可以认为回波信号是发射信号乘以幅度衰减因子A(t)并附加一定的延迟τ0和随机相位ϕ(t)而得到。数学表达式为

由式(1)和式(2)可得

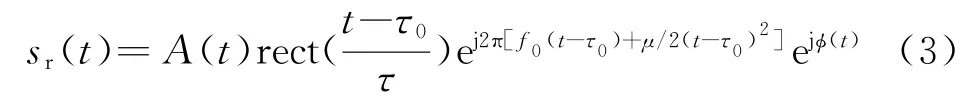
地、海杂波可以认为是面杂波,云雨、气象杂波则是体杂波。无论是面杂波还是体杂波,都是基于点目标来模拟的。单个雷达分辨单元内的目标可以看作点目标来处理。单个点目标的回波信号可以表示为

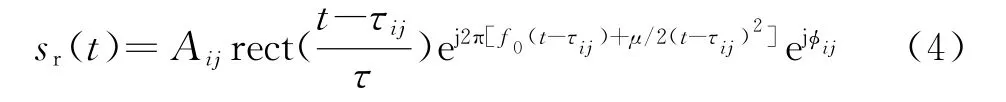
式中,A ij可以通过雷达方程得到,它的具体值为

式中,r ij为杂波单元到雷达之间的距离,σ0S ij为杂波单元的雷达横截面积(σ0是杂波的后向散射系数,S ij是杂波单元面积),G ij为杂波单元对应的天线增益,n ij为杂波的调制系数。

1.2 导弹轨迹方程的确定

比例导引法是现代导弹制导中较常见的一种方法,它是指导弹在攻击目标的过程中,导弹速度矢量的旋转角速度与目标线的旋转角速度成固定比例的一种导引方法。它克服了直接追踪法弹道弯曲和平行接近法对控制系统要求严格的缺点,在工程上容易实现。通过目标飞行的特点选择合适的导引系数k,就可以实现较高的追踪效率。对于不同机动特性的目标适应能力也比较强,因此广泛应用于各种类型的导弹上,它的原理结构图如图1所示。

图1中,A为导弹的位置,M为目标的位置,vm为导弹的速度,vt为目标的速度。比例导引法制导的相对运动方程组为

式中,r为目标与导弹的距离,ηt,η分别为目标和导弹速度矢量的前置角,k为比例系数,σt为航向角,σ为导弹导引角,θ为目标线角。

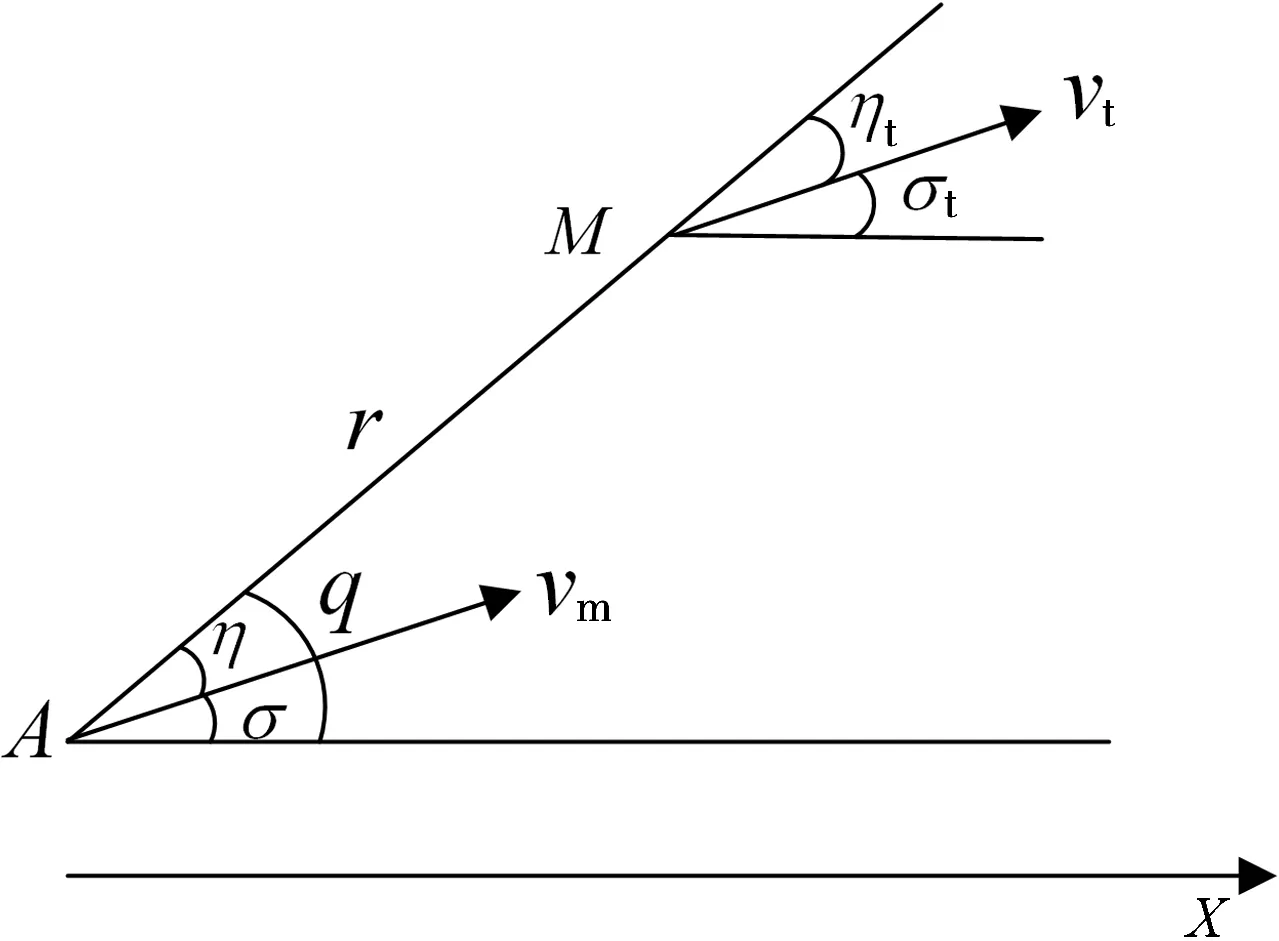
图1 比例导引示意图

1.3 仿真场景的设置

本文所设置的仿真场景是弹载导引头在向海面目标飞行的过程中,海杂波对导引头上雷达回波信号的影响。

1.3.1 波束单元照射面积的划分

对面杂波的仿真,通常是将雷达波束照射单元划分成许多小的距离单元,每一个小的距离单元反射的电磁波强度、方位均不相同,对这类波束照射区域为面杂波时,采用经典而又高效的处理方法——网格映像法[4]。网格映像法是根据雷达的距离分辨率和方位分辨率来将照射区域划分成许多独立的小网格,每一个网格可以认为是点目标,计算每一个网格的回波信号,最后再将所有网格内的回波信号进行相干叠加,得到总的回波信号。原理图如图2(a)、(b)所示。

图2(a)、(b)中,VR是雷达平台的速度,φ是网格单元的擦地角,θ是方位角,Δr是距离分辨率,Δθ是方位角的分辨率,R是雷达到网格单元的距离,H是雷达平台的高度。根据文献[5]可知,网格单元的距离分辨率和方位分辨率分别为

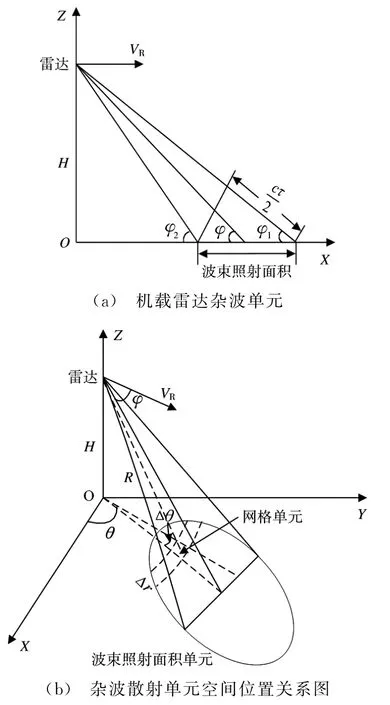
图2 网格映像法原理图

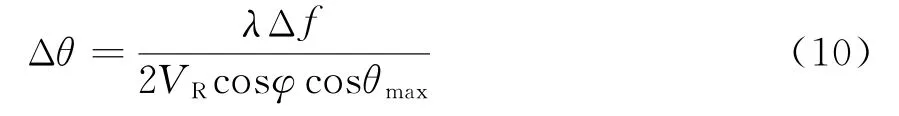
式中,τ为雷达发射信号的脉宽,θmax为杂波散射单元的最大方位角,Δf为多普勒分辨率,Δf=,其中fr是脉冲重复频率,N是雷达发射脉冲串个数。

1.4 杂波功率谱特性和幅度统计特性的计算

目前,对杂波统计建模的研究主要为统计特性和功率谱特性。杂波是随机起伏信号,其功率谱特性可以用功率谱密度或自相关函数来表示。常用的杂波功率谱模型有高斯模型、Cauchy模型,以及全极点模型。本文采用高斯谱来进行仿真,它的表达式为

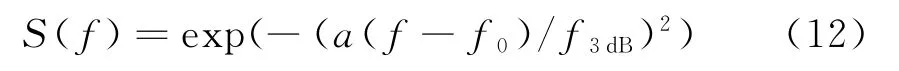
式中,f0为频谱最大点的位置,通常令f0=0;f3dB为两个半功率点的波束宽度,它由海情及雷达的波长所决定;a的取值满足S(f3dB/2)=0.5,解得

杂波的幅度统计特性与雷达的分辨率、波束入射角等因素有关。常用的杂波幅度模型有瑞利分布、对数正态分布、Weibull分布和K分布等。这些幅度统计模型与雷达平台参数、海情、入射角和极化等因素有关,适用范围如表1所示。

表1 杂波幅度模型

产生杂波序列的方法一般有两种:零记忆非线性法(ZMNL)和球不变随机过程法(SIRP)。由于SIRP受所求序列的阶数及自相关函数的限制,同时这种方法的计算量非常大,不易形成快速算法,而ZMNL方法克服了这种缺陷。但ZMNL中输入序列和输出序列存在着复杂的非线性关系,文献[6]对此进行了很好的总结,使得这种非线性关系已经明确。本文采用ZMNL产生相干相关的K分布,它的原理图如图3所示。

图3 ZMNL产生K分布示意图

z i的幅度分布特性由非线性变换(ZMNL)获得,功率谱特性通过滤波器H(w)获得。使用ZMNL法时应先求得z i和w i相关函数之间的非线性关系,然后再求得v i,即通过z i的相关系数s ij求得v i的相关系数ρij,然后再确定滤波器H(w),这里

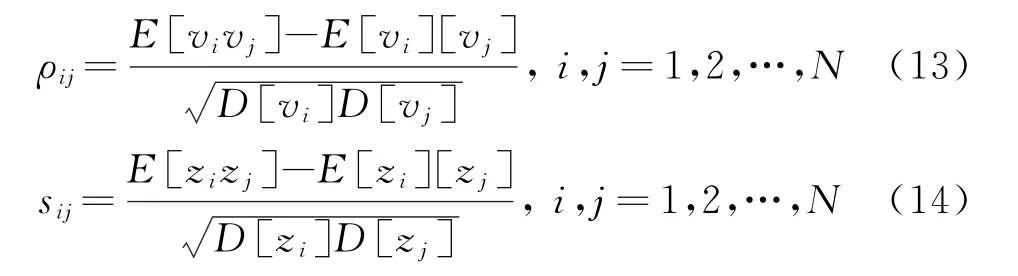
H(w)可由下式得到:

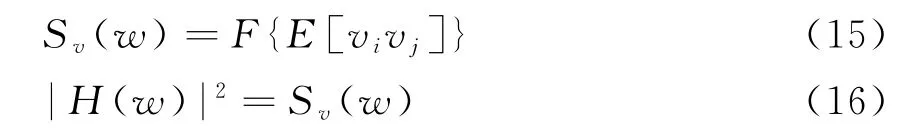
H(w)得到后可以通过频域法得到{v i}。

2 仿真实验

海杂波回波信号产生的流程如图4所示。

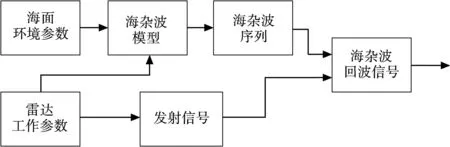
图4 海杂波回波信号产生的流程

具体的参数值如表2所示。

表2 仿真参数设置

图5(a)、(b)分别为线性调频信号的时域波形和频谱图,可以看出线性调频信号的频谱类似与矩形窗函数,这是因为频率的线性变化,使得能量平均分布在各个频点上。

图6为仿真的K分布与理论K分布的对比,K分布的形状参数为v=2,尺度参数a=0.5;可知,生成的海杂波PDF与理论值大致相吻合,说明了用球不变的随机过程法实现杂波模拟的有效性。图7为仿真杂波的功率谱与理论值对比,功率谱为高斯谱,f3dB=40 Hz,模拟产生杂波的功率谱采用Burg法估计,可知仿真的结果与理论值大致相吻合。

图8 为产生的K分布杂波序列的实部和虚部,杂波序列长度为4 096点。

仿真产生的海杂波回波信号及其频谱如图9(a)、(b)所示,图9(a)仿真的是50μs内海杂波的回波信号,图9(b)是回波信号的频谱,可知,幅度在-55～-70 dB之间。

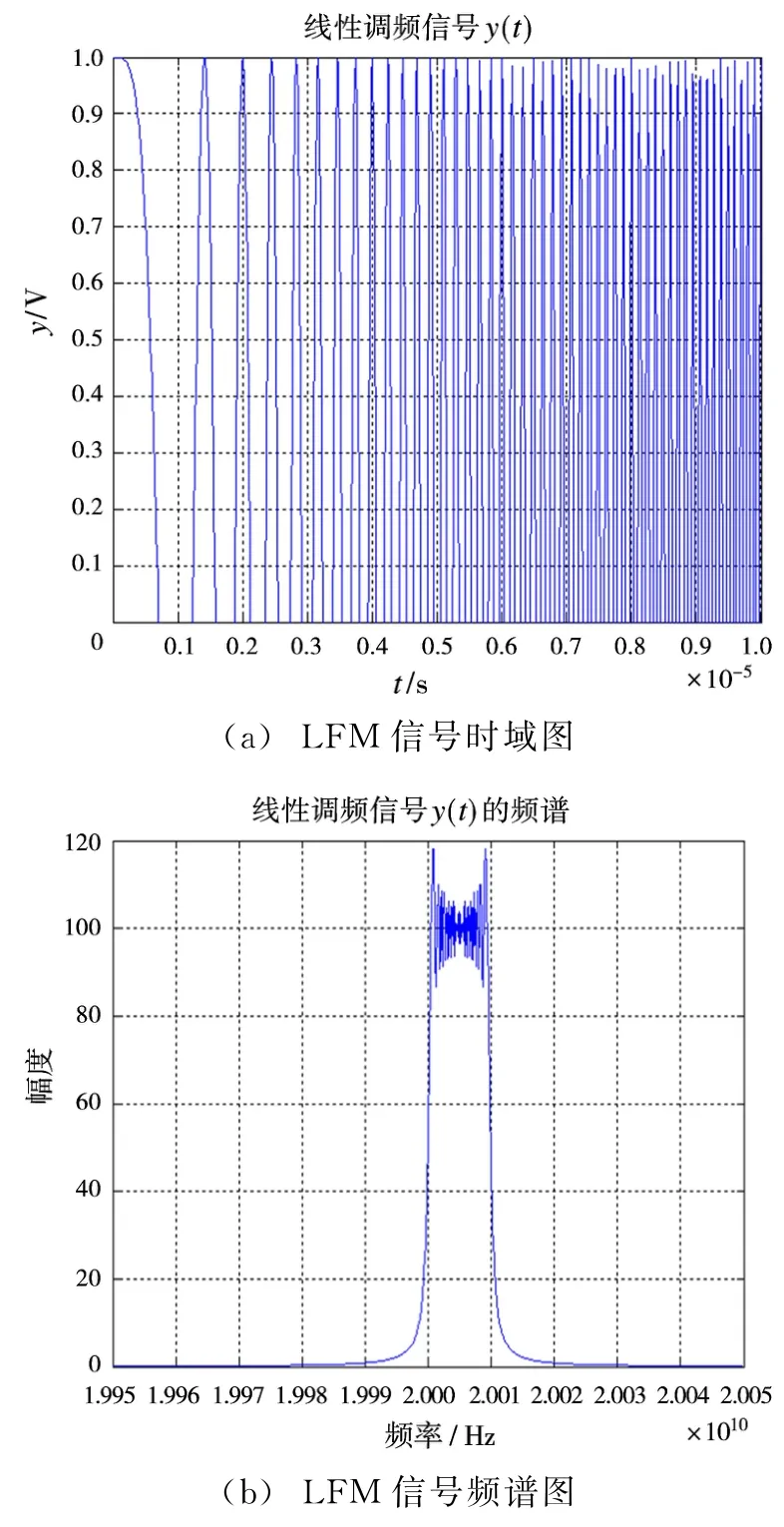
图5 线性调频信号时域与频谱图

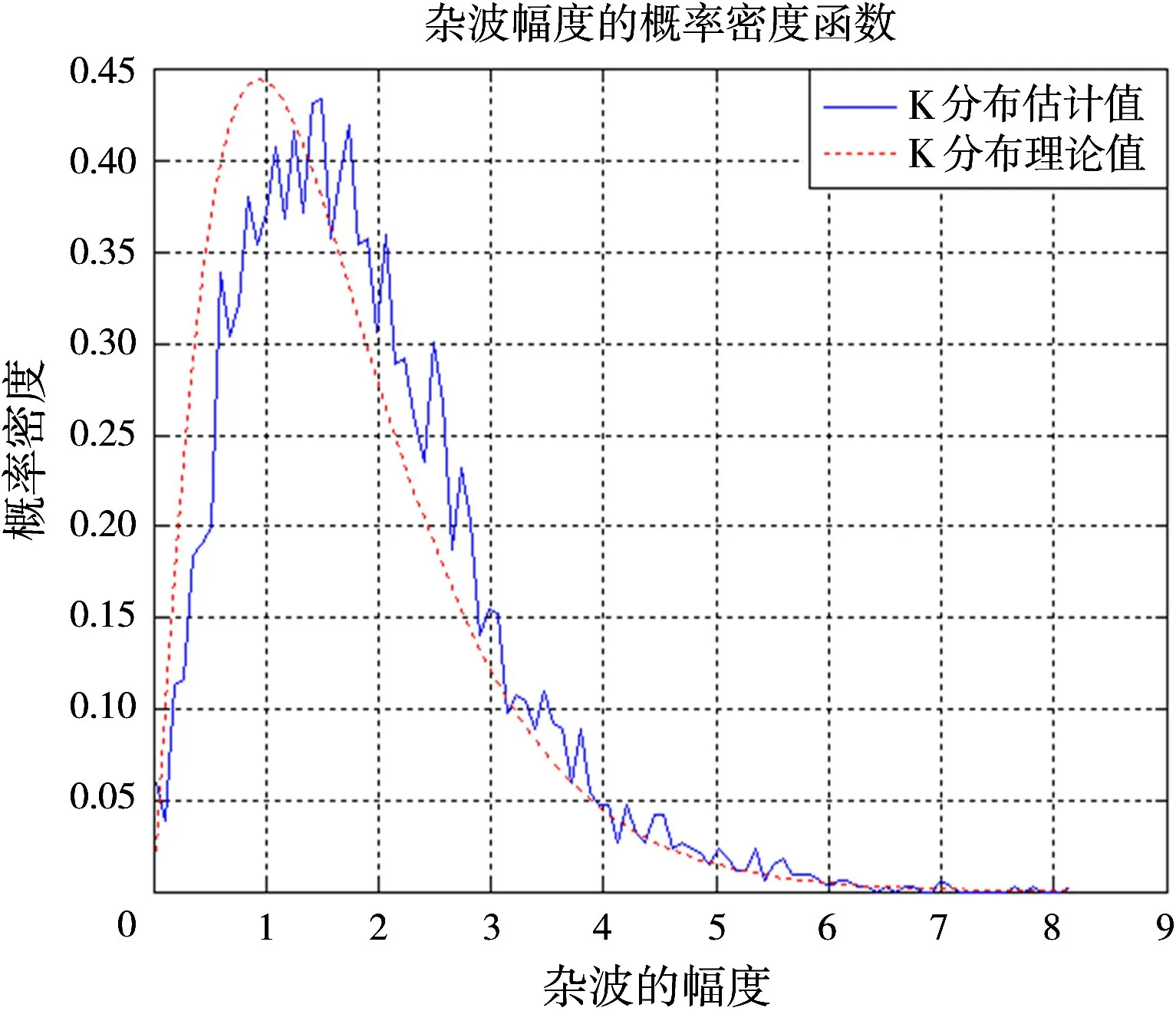
图6 幅度分布与理论分布对比

图7 功率谱与理论对比

图8 仿真产生杂波序列的实部和虚部

3 结束语

本文对PD雷达导引头所面临的背景环境——海杂波进行了仿真建模和频谱分析,对海杂波的一些散射特性,如后向散射系数、幅度统计特性和频谱特性进行了仿真分析,仿真实验得出的结果与理论值相符。最后对海杂波的回波信号进行了仿真分析,本文所设置的发射信号比较简单,雷达发射信号的参数,如脉冲重复频率、带宽和调频系数等对海杂波回波信号影响没有进行深入讨论,这也是后续工作所要研究讨论的地方。本文的仿真模型和实验结果可以作为海杂波中目标信号检测的基础。

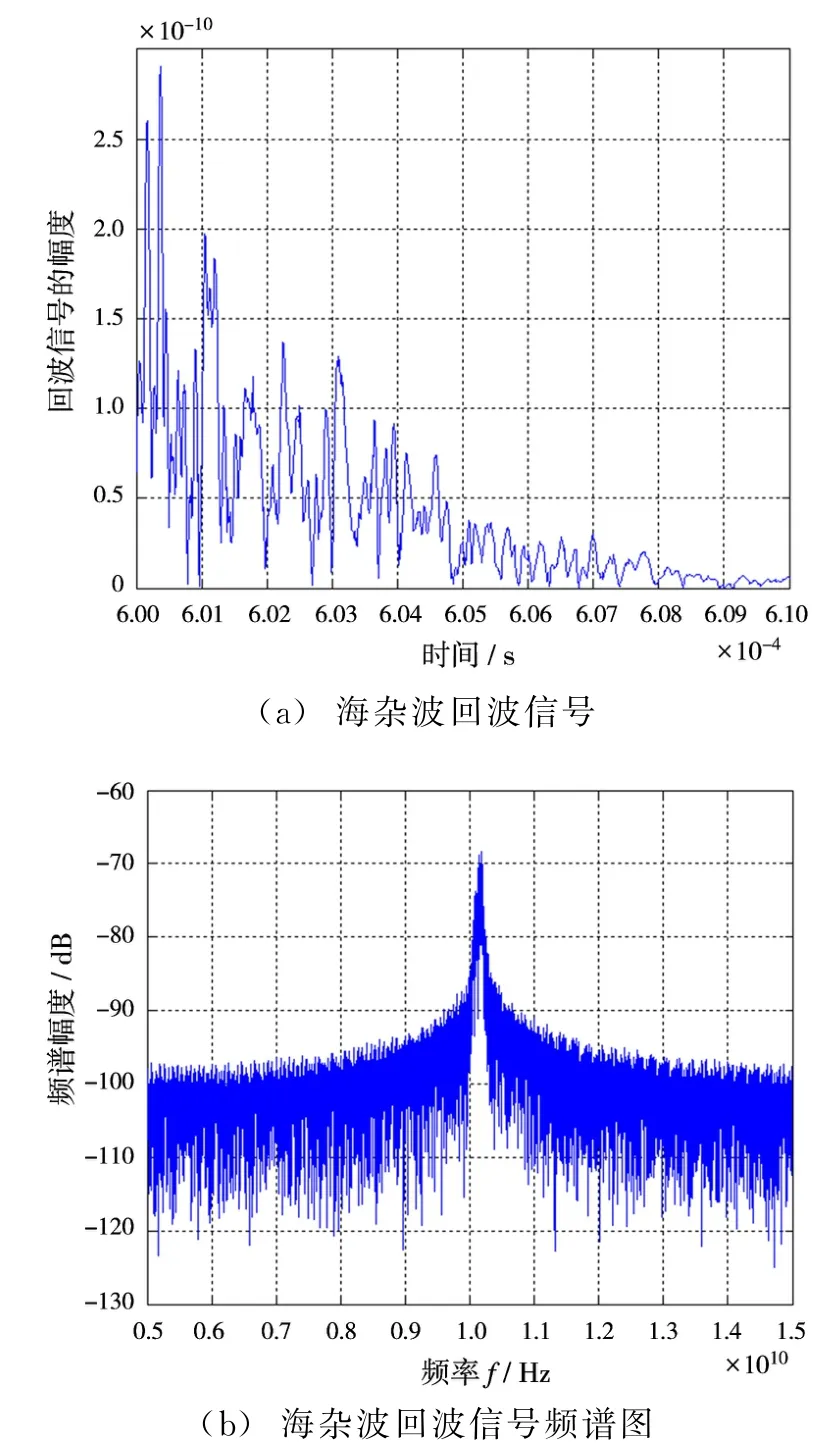
图9 海杂波回波信号及其频谱图

[1]WARD K D,WATTS S.Use of Sea Clutter Models in Radar Design and Development[J].IET Radar,Sonar and Navigation,2010,4(2):146-157.

[2]姜斌.地、海杂波建模及目标检测技术研究[D].长沙:国防科学技术大学,2004.

[3]杨俊岭,吕韶昱,万建伟.一种新的相干K分布模型及其在海杂波仿真中的应用[J].系统仿真学报,2007,19(2):250-253,260.YANG Jun-ling,LV Shao-yu,WAN Jian-wei.A New Coherent K-Distributed Model and Its Application in Sea-Clutter Simulation[J].Journal of System Simulation,2007,19(2):250-253,260.(in Chinese)

[4]李芾.基于实测海杂波数据的统计特性分析[D].西安:西安电子科技大学,2013.

[5]谢洪森,邹鲲,周鹏.低掠射角海杂波的统计特性分析[J].雷达科学与技术,2011,9(2):172-179.XIE Hong-sen,ZOU Kun,ZHOU Peng.Statistical Analysis of Sea Clutter at Low Grazing Angle[J].Radar Science and Technology,2011,9(2):172-179.(in Chinese)

[6]MOREAU I.Study and Simulation of Sea Clutter[C]∥IEEE Signal Processing Workshop on Higher-Order Statistics,South Lake Tahoe,CA,USA:IEEE,1993:178-181.