一种抗速度欺骗干扰的认知波形设计方法∗

(电子科技大学电子工程学院,四川成都611731)

0 引言

随着基于数字射频存储器(DRFM)的现代欺骗式干扰技术的出现,雷达干扰技术步入相干干扰时代[1-2]。在电子战中,敌方侦察电子设备捕获到我方雷达的探测信号后,会产生电子欺骗干扰,对我方雷达探测形成距离欺骗、速度欺骗以及假目标等多种形式的干扰,从而降低了我方雷达的探测性能。因此,为保证雷达在干扰坏境下对目标的正确检测和跟踪,增强雷达的抗有源欺骗干扰能力显得尤为重要。

由于干扰机产生干扰信号需要一定的时间,干扰信号至少滞后雷达一个或数个脉冲重复周期,故脉冲分集技术是对抗有源欺骗干扰的一个有效措施[3]。文献[4]在研究针对SAR的有源欺骗干扰对抗问题上提出了基于相位扰动和基于调频率扰动两种脉冲分集波形设计方案,并通过对干扰信号加以惩罚的方法来抑制干扰,但该方法仅能针对线性调频雷达,应用范围受限。文献[5-6]针对雷达欺骗干扰,提出了一种以脉冲分集技术为基础,在一定的脉冲重复周期间发射特定分组编码信号进行抗干扰的方法,在对接收信号按发射编码进行匹配滤波后,该方法在特定的距离单元可以有效地对干扰信号进行对消从而达到抗干扰的目的,但无法克服正交波形带来的距离旁瓣影响。文献[1]在文献[6]的基础上研究了快慢时域联合的波形设计方法和基于OFDM的波形设计方法来对抗密集复制假目标干扰和C&I假目标干扰。文献[7]通过设计相互正交多脉冲信号并通过二维频域运动补偿的方式来对抗距离欺骗干扰。

以上文献中所提到的方法均是用来对抗距离欺骗干扰的,对于抗速度欺骗干扰的波形设计方法研究较少。文献[8]利用多通道处理技术对干扰参数进行估计,并通过设计脉间相位编码波形自适应的对抗速度欺骗干扰,该方法可在强电子干扰环境中有效检测单个真实目标,但文章中未考虑多个真实目标的情况。本文在此基础上作改进,提出一种多目标多干扰场景中的抗速度欺骗干扰波形设计方法。首先,建立了速度欺骗干扰下的雷达回波模型;然后,根据阻带干扰能量最小准则构建优化问题,并利用循环迭代算法得到最优的发射波形;最后,通过仿真验证本方法在多目标强干扰场景中对抗速度欺骗干扰的有效性。

1 雷达回波模型

考虑脉间编码波形作为雷达发射波形,即在每个简单脉冲上调制一个初始相位。第n个发射脉冲复基带形式的复包络可以表示为

式中,Tr为雷达发射脉冲重复间隔,N为一个相干处理间隔(CPI)内脉冲个数,ϕn为第n个发射脉冲的初始相位,且ϕn∈[-π,π]。u(t)是宽度为Tp的简单脉冲的复包络,其表达式为

假设雷达天线主瓣内有Q个真实目标(均视为点目标),目标散射系数为目标与雷达的径向速度为v q(q=1,2,…,Q),不失一般性,将目标的多普勒频移归一化,即其中λ为雷达发射信号波长。经真实目标反射的雷达回波信号可以建模为

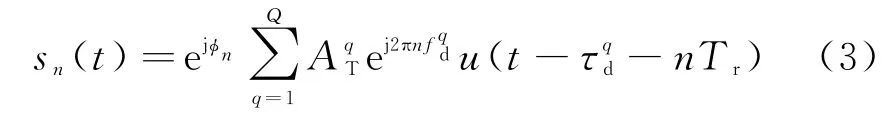
对于高重频PD雷达,一个CPI内周围环境和目标状态的变化是微小的,可以认为目标是保持静止的,故假定一个CPI内每个真实目标的散射系数、双程时延和多普勒频移均保持不变。

干扰机在截获雷达信号后对其进行复制并调制信号的多普勒参数,然后将干扰信号转发回雷达接收机形成速度欺骗干扰。干扰机为了对雷达进行有效的速度欺骗,其转发的假目标干扰信号多普勒在捕获雷达速度波门后逐渐增大或减小(速度波门拖引),将雷达的速度波门拖开而跟踪上假目标,从而保护真实目标;或是产生与真实目标多普勒相近的多个强干扰信号,迷惑雷达、消耗雷达资源,甚至使真实目标淹没在假目标之中难以检测出来。

考虑每个真实目标上均携带有一个基于DRFM的干扰机,且每个干扰机能同时产生多个速度假目标信号。由于干扰机截获分析复制雷达信号需要一定的时间,干扰滞后雷达信号i(1≤i≤N)个PRI,即干扰机每次通过多次复制上一个PRI的雷达脉冲,经多普勒调制后将干扰信号转发回雷达接收机。假设经干扰机调制后产生的速度假目标信号的幅度相互独立,多普勒频率也相互独立。

通过以上分析,雷达接收机第n个PRI内的干扰信号可以表示为

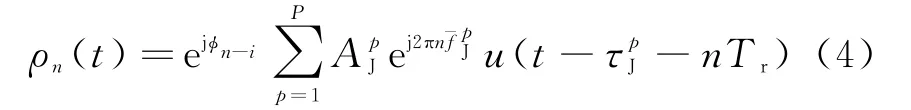
忽略脉内噪声影响,则雷达接收端在第n个PRI内的接收信号为

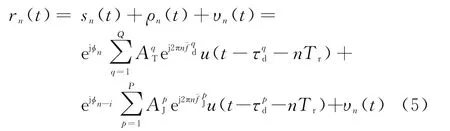
式中,υn(t)为加性高斯白噪声。

认知雷达可根据雷达回波估计目标和干扰的相关参数,为简化模型,我们作以下假设:

假设3 第p(p=1,2,…,P)个假目标的幅度归一化多普勒频率以及干扰滞后雷达的脉冲重复周期个数i均为雷达通过认知流程估计得到的先验信息。

根据以上假设可知,第n个接收脉冲在τd处的匹配滤波输出为

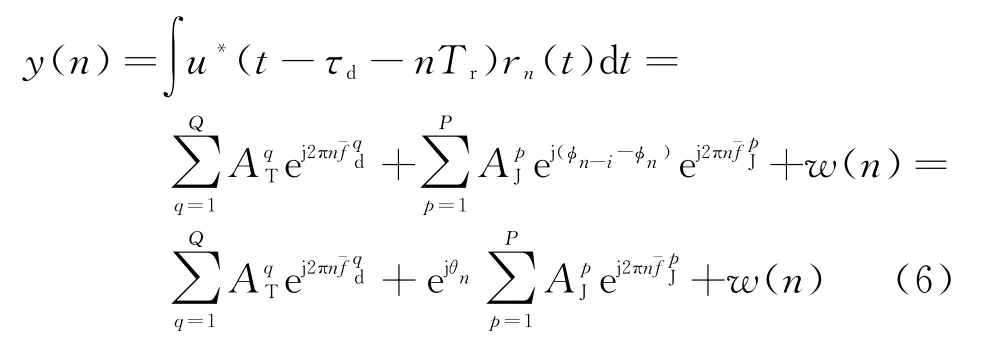
式中,θn=ϕn-i-ϕn(n=1,2,…,N),ϕ1-i,ϕ2-i,…,ϕ0为[-π,π]内给定的任意值,w=[w(1),w(2),…,w(N)]T是方差为σ2的高斯白噪声。

分析式(6)可知,当发射信号的初始相位ϕn(n=1,2,…,N)随机均匀分布时,θn(n=1,2,…,N)也服从均匀分布,且干扰信号的能量由于受θn的影响将会均匀分布在整个多普勒频谱上,而真实目标信号的匹配滤波输出不受θn的影响,其能量不会扩散,故采用脉间随机相位编码脉冲可以有效抑制速度欺骗干扰,但当干信比高于10 log10NdB时,真实目标将会被干扰淹没而无法检测出来[8]。

2 抗速度欺骗干扰波形设计

针对强干扰情况下真实目标被掩盖而无法检测的问题,本文利用认知流程获取目标和干扰的先验信息,从波形设计的角度出发,在每个可能存在目标的附近设置一个阻带,尽可能地抑制阻带内的干扰能量,从而提高阻带内目标的信干噪比,改善雷达的抗干扰性能。

根据Q个真实目标的多普勒估计值2,…,Q),为确保每个真实目标多普勒均位于阻带内,设置阻带,其中Ns(Ns≤Q)为阻带个数,f k1,f k2分别为第k(k=1,2,…,Ns)个阻带的上下限。

根据式(6)可知,等式右侧第2部分为第n个接收脉冲内的干扰信号在τd处的匹配滤波输出,令

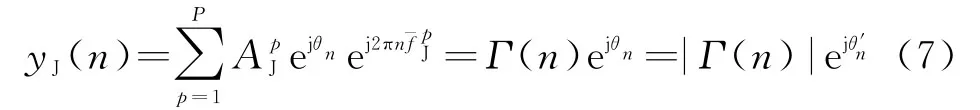
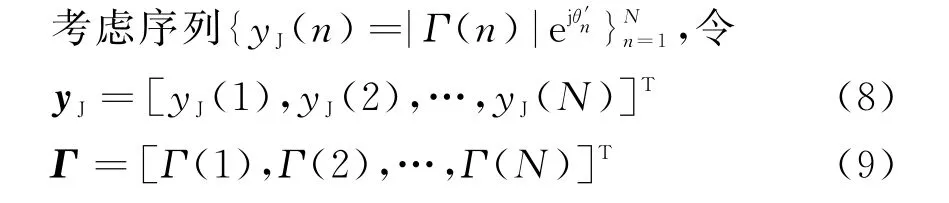
定义矩阵S为F~N中的某些列(这些列表示的频率点与Ω中频率相对应)组成的矩阵,定义G为中除去S对应的列向量所构成的子矩阵。如:取则S为中第100列到200列构成的子矩阵,则中除去第100列到200列构成的子矩阵。

根据矩阵S和G的构成关系,式(11)可以等价于

式中,α为辅助变量。

当x固定时,C(yJ,α)是一个关于α的线性函数,对α求导,由于GHG=I,令可得使C(yJ,α)取得最小值的α:

当α固定时,其中c为Gα的前N个元素组成的向量,可求得使C(yJ,α)取得最小值的yJ:

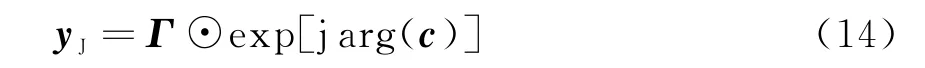
利用循环迭代法可以求得式(12)的最优解,并求解出下一个CPI内的相位编码序列具体算法步骤如下:

1)u=0,随机初始化序列yJ。

2)令u=u+1,固定yJ,计算使C(yJ,α)取得最小值的

3)固定α,计算使C(yJ,α)取得最小值的令c为Gα的前N个元素组成的向量exp(jarg(c))。

5)由yJopt和式(7)可以求得序列然后,由给定的ϕ1-i,ϕ2-i,…,ϕ0,可以求得下一个CPI内每个发射脉冲的编码相位

3 仿真结果

定义第q(q=1,2,…,Q)个目标的输入信噪比为

定义第p(p=1,2,…,P)个干扰相对于第一个真实目标的输入干信比为

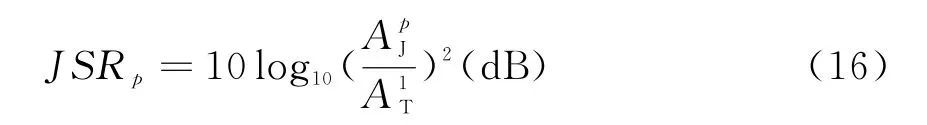
考虑高重频雷达主瓣内有1个或多个真实目标,每个真实目标均携带有基于DRFM的干扰机可对雷达实施速度假目标干扰,且所有真实目标与假目标均在同一距离单元。选取一个CPI脉冲数N=512,噪声功率为1,FFT点数为8 192,蒙特卡洛仿真100次。

仿真1 对比固定发射波形与随机相位编码波形的抗速度欺骗干扰性能

仿真中真实目标出现在0.1 Hz,而速度假目标在0.12 Hz,由图1(a)和(c)中可知,采用固定发射波形时,多普勒谱上会出现两个目标,雷达无法分辨真假目标;而从图1(b)和(d)中可以看出,采用随机相位编码波形时,假目标能量会扩散在整个多普勒谱,在JSR较小时,真实目标能被检测出来,而当JSR较大时,真实目标被干扰能量所掩盖而无法检测。

仿真2 本文算法抗速度欺骗干扰性能

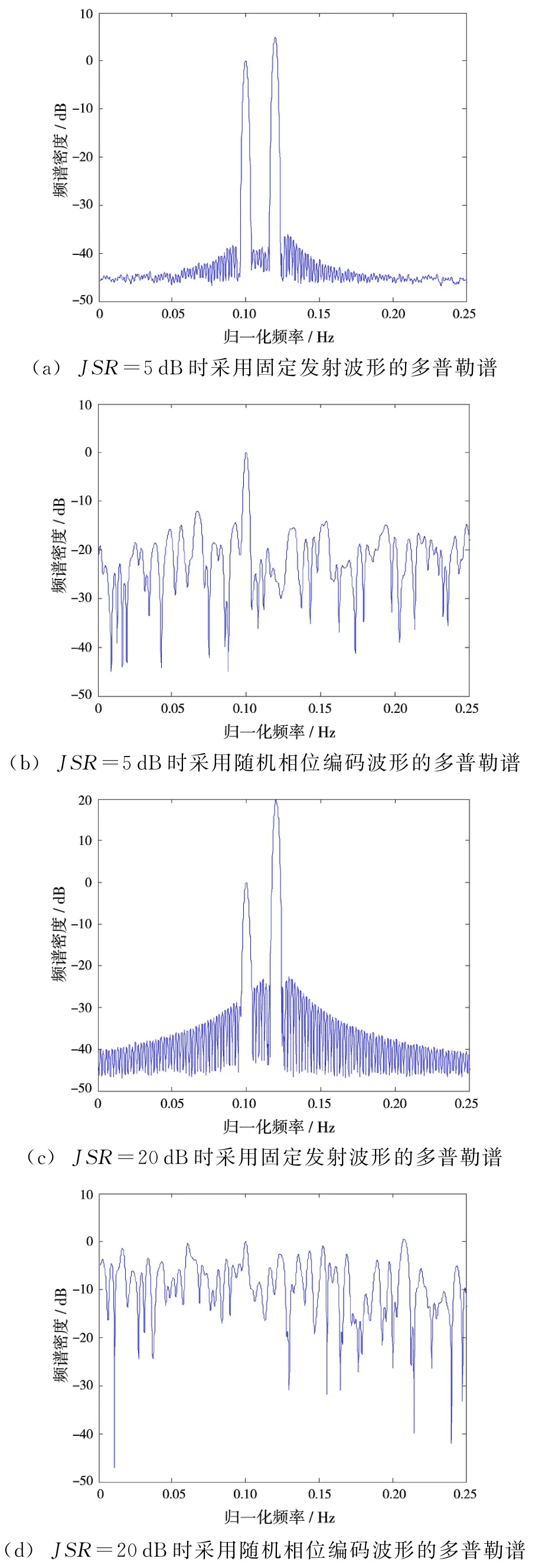
图1 不同干信比下采用固定发射波形与随机相位编码波形的多普勒谱

干扰机在第1,2个真实目标附近均产生有多个强假目标干扰,真实目标被干扰掩盖而难以检测,第3个目标为弱小目标,输入信噪比极低,其被强干扰的多普勒旁瓣所淹没而不易检测;图2(b)中,采用随机相位编码脉冲时,由于干扰能量扩散到整个多普勒谱,完全掩盖了真实目标;从图2(c)中可以看出,采用本文算法设计的波形作为发射波形时,经多普勒处理后在3个真实目标附近均形成阻带,阻带内的干扰得到抑制,信干噪比分别可达40.5,28.5和10 dB,且弱小目标也能被检测出来。此外,从图2(d)中可以看出,本算法收敛速度极快,经过20次迭代后,就可获得抗干扰性能较好的相位编码脉冲。

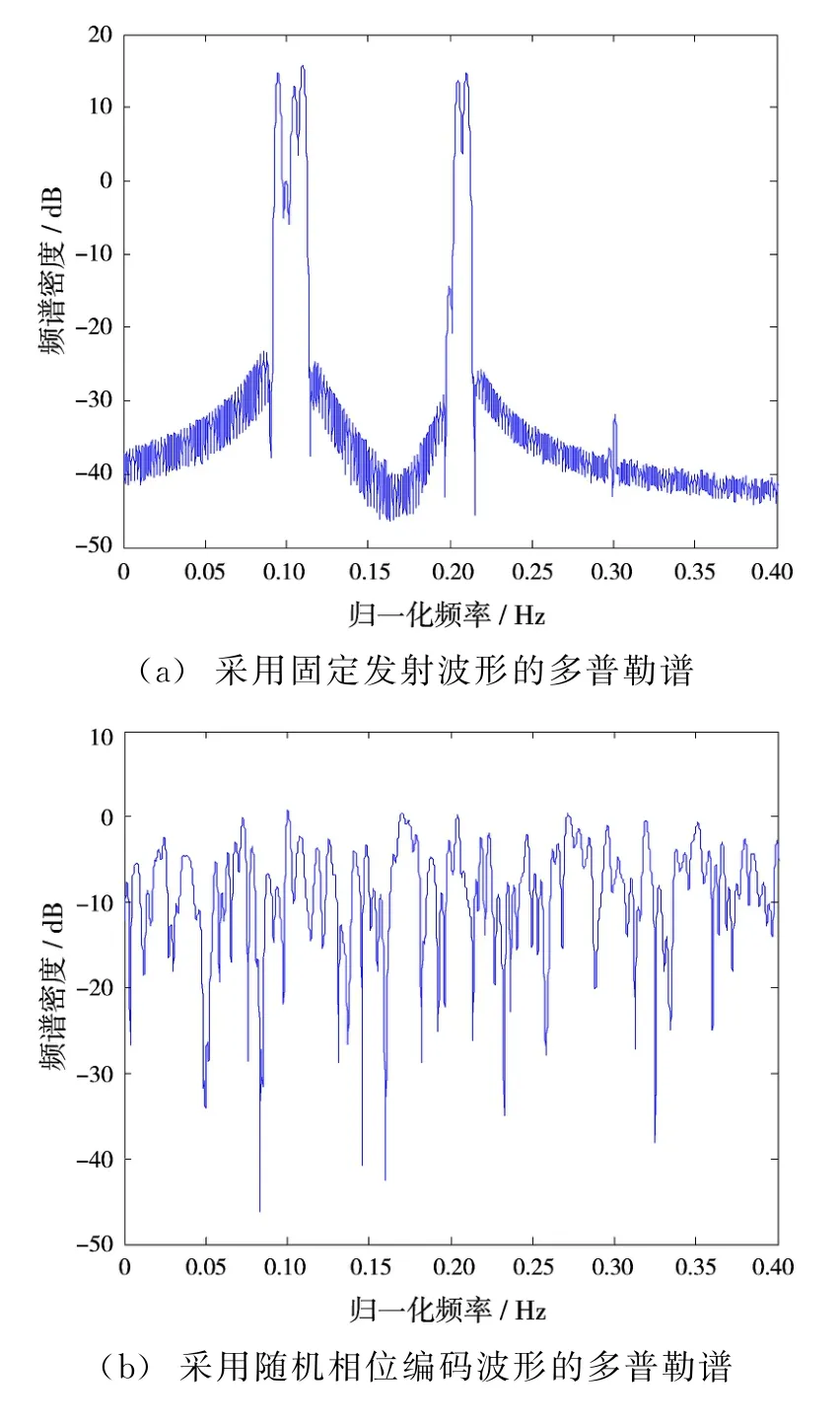
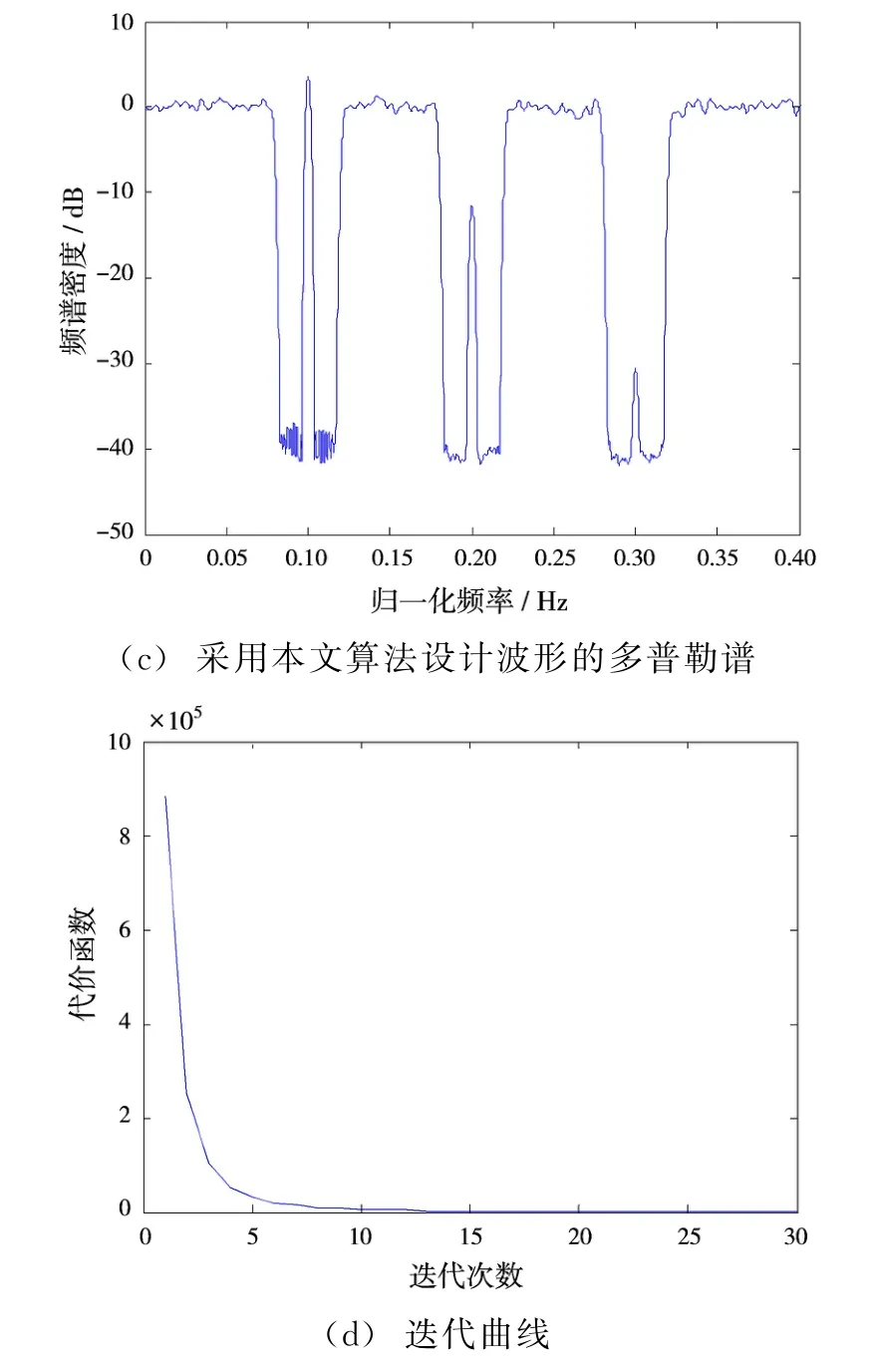
图2 多目标多干扰下采用本文算法设计波形的多普勒谱

4 结束语

速度欺骗干扰会影响雷达对真实目标多普勒的检测,使雷达跟踪错误的目标或检测到多个虚假目标,本文针对这个问题,从波形设计的角度出发,提出了一种脉间相位编码波形设计算法。该算法可在强干扰条件下,抑制阻带内的干扰,实现雷达对多个真实目标的正确检测,提高雷达的抗干扰性能,且对于淹没在多普勒旁瓣中的弱小目标,该算法也有较高的信干噪比改善。

[1]卢刚.雷达有源假目标抑制方法研究[D].成都:电子科技大学,2012.

[2]张勇强,于孝松.基于FFT的有源欺骗干扰抑制[J].雷达科学与技术,2013,11(6):663-667.ZHANG Yong-qiang,YU Xiao-song.Suppression of Active Deception Jamming Based on FFT[J].Radar Science and Technology,2013,11(6):663-667.(in Chinese)[3]LI N J,ZHANG Y T.A Survey of Radar ECM and ECCM[J].IEEE Trans on Aerospace and Electronic Systems,1995,31(3):1110-1120.

[4]SOUMEKH M.SAR-ECCM Using Phase-Perturbed LFM Chirp Signals and DRFM Repeat Jammer Penalization[J].IEEE Trans on Aerospace and Electronic Systems,2006,42(1):191-205.

[5]AKHTAR J.An ECCM Scheme for Orthogonal Independent Range-Focusing of Real and False Targets[C]∥Proceedings of the IEEE Radar Conference,[S.l.]:[s.n.],2007:846-849.

[6]AKHTAR J.Orthogonal Block Coded ECCM Schemes Against Repeat Radar Jammers[J].IEEE Trans on Aerospace and Electronic Systems,2009,45(3):1218-1226.

[7]LEI X,NAN L,SHANSHAN Z,et al.A Radar ECCM Method Based on Orthogonal Pulse Block and Two-Dimensional Frequency Domain Motion Compensation[C]∥IET International Conference on Radar Systems,[S.l.]:[s.n.],2012:1-4.

[8]ZHANG J.New Antivelocity Deception Jamming Technique Using Pulses with Adaptive Initial Phases[J].IEEE Trans on Aerospace and Electronic Systems,2013,49(2):1290-1300.

[9]STOICA P,HE H,LI J.New Algorithms for Designing Unimodular Sequences with Good Correlation Properties[J].IEEE Trans on Signal Processing,2009,57(4):1415-1425.

[10]HE H,STOICA P,LI J.Waveform Design with Stopband and Correlation Constraints for Cognitive Radar[C]∥2010 2nd International Workshop on Cognitive Information Processing(CIP),[S.l.]:IEEE,2010:344-349.