机动目标无源跟踪IMM-MKF算法∗

(海军航空工程学院电子信息工程系,山东烟台264001)

0 引言

现代高科技局部战争的经验表明,制空权和信息快速获取能力已成为决定战争胜负最为关键的两个因素,两者密不可分。在这种背景下,多站尤其是运动多站无源定位跟踪系统[1-2]因为具有信息融合能力、隐蔽性好、机动性强、探测距离远等优点,已成为获取战场信息的重要手段,获取战场中机动目标的状态信息是一个难点。

目前对机动目标的跟踪多采用交互式多模型结构,研究的重点在于模型集的选择和与模型集对应的滤波算法性能的改进[3-6]。本文对后者进行研究。

目前,非线性滤波算法主要有三类:一是基于局部线性化的扩展卡尔曼滤波(EKF)类算法[7]。当系统方程非线性程度较高时EKF类算法线性化误差大,跟踪性能不稳定。二是基于确定性采样点的sigma点卡尔曼滤波算法,包括不敏卡尔曼滤波(UKF)[8-9]算法、容积卡尔曼滤波(CKF)算法[10]等。这类算法采用一组带有权值的确定性采样点来近似统计量的均值和方差信息,可视为EKF算法的改进,目前应用比较广泛,尽管跟踪精度有所提高,不过仍未解决EKF类算法的缺点。三是基于随机采样点的粒子滤波类算法[11]。尽管理论上粒子滤波类算法能很好地近似后验概率密度函数,但这需要无穷多随机采样点,实际应用中只能选择有限的采样点且存在粒子退化现象,导致粒子滤波算法计算量大且跟踪性能不理想。

为了更好地利用sigma点卡尔曼滤波算法的确定采样点,文献[12]提出了一种新的变换即边缘化变换(MT)来计算随机变量的前两阶矩信息(均值和方差)。边缘化变换采用与UKF算法或者CKF算法相同的sigma点,不过将非线性函数建模为随机过程并进一步将其描述为一系列Hermite多项式的线性组合,从而可以得到均值和方差的解析闭式解,保证了协方差矩阵的半正定性。MT假设Hermite多项式的系数具有分级先验分布,这些系数的后验概率分布可以通过变换后的sigma点求出,对系数进行积分可以消除其影响从而解析计算出变换后的均值和方差信息。

本文将MT应用于状态更新过程,提出了基于MKF的新的运动多站无源跟踪算法,将其与IMM结合来实现对机动目标的高精度跟踪,并对其性能进行了仿真分析。

1 机动目标跟踪模型

考虑具有如下Markov跳变线性系统的机动目标状态估计问题。

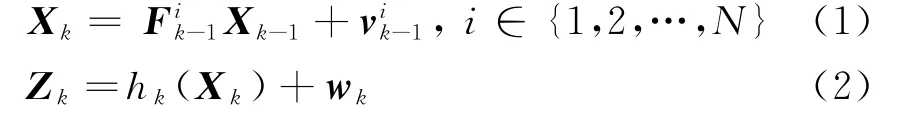
式中,X k和Z k分别表示k时刻目标的状态及运动观测站获得的观测量(本文采用的观测量为角度),表示k-1时刻目标按第i个模型运动时的状态转移矩阵,h k为与目标状态及观测站状态有关的非线性函数,过程噪声与测量噪声w k～N(0,R)相互独立。假设目标在N个模型之间依Markov链进行转移,转换概率已知且k-1时刻模型转移到k时刻模型j(记为

2 IMM-MKF算法

2.1 MKF算法

假设已知N个模型的初始状态估计都为E[X0],初始协方差矩阵估计P0=E[(X0-对k∈{1,…,∞},因为状态方程为线性,在最小均方根误差(MMSE)准则下卡尔曼滤波(KF)是最优滤波器,因此对第i个模型而言状态预测过程通过KF来实现,即

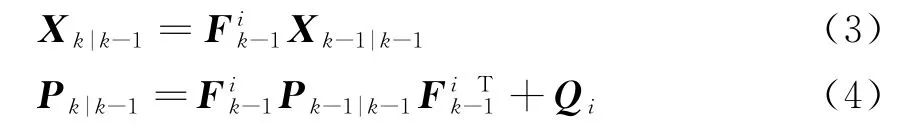
量测方程为非线性,本文采用M T来实现状态更新,具体步骤为:

1)选择先验分布矩阵Σ,该矩阵是p×p的对角矩阵(p≤5),对角元素至少两个非零。先验矩阵为对角矩阵是因为假设θj的各个元素服从高斯分布且相互独立。p≤5是因为M T最多能够准确积分直到5阶的多项式。

2)产生2n+1个sigma点χ=[X0,X1,…,X2n],即

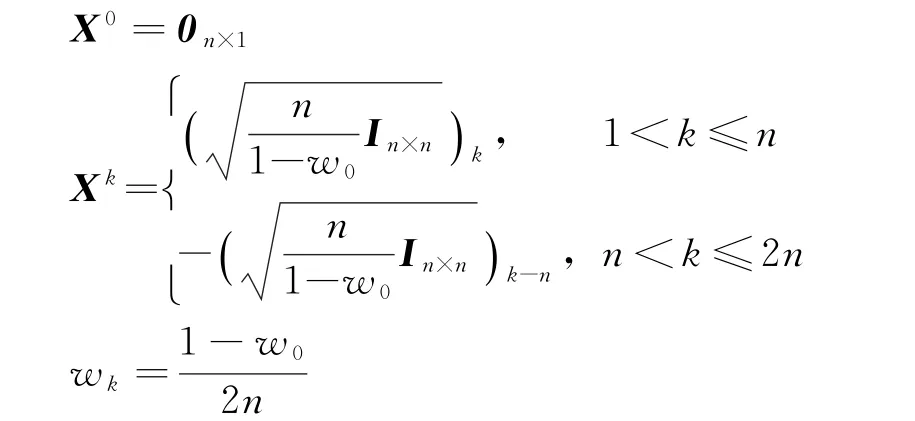
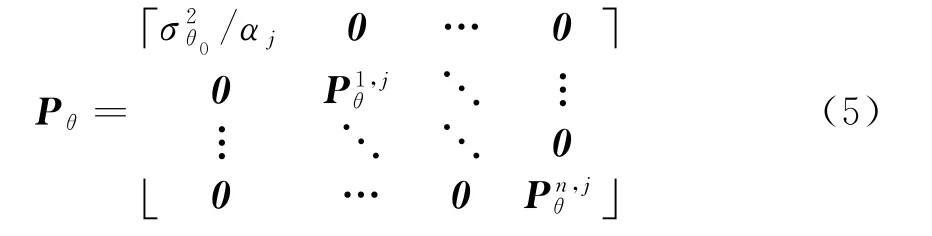
式中,w和C为Hermite基函数的均值和协方差矩阵,C为对角矩阵,其对角元素如式(7)所示,H(χ)为在各sigma点处计算的Hermite多项式,Pθ|z为加权矩阵θ的后验分布。式(6)～式(9)在递推过程中为常量,可以提前计算,从而大大减小算法计算量。

4)求解变换后的sigma点即根据χ计算的观测量点集

5)计算k时刻观测量的一步预测值^Z k|k-1

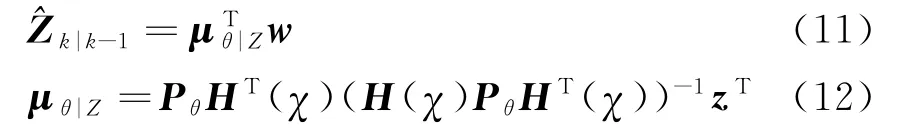
6)估计θi,j先验分布中的比例因子αj,用众数作为其估计值,即

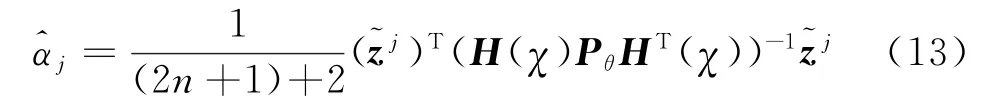
7)计算观测量一步预测值的协方差矩阵

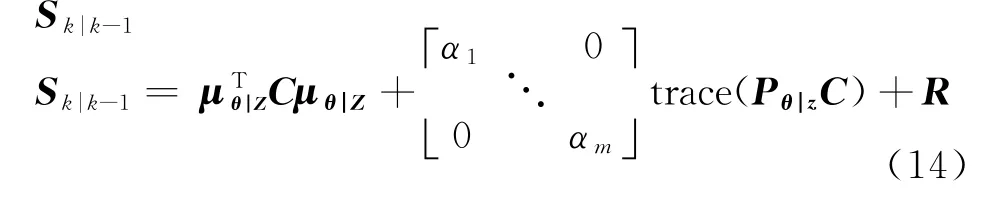
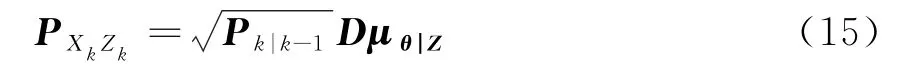
权增益及状态更新过程与KF相同

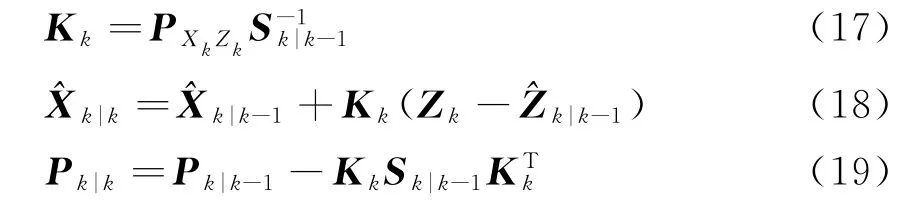
通过上面推导可知,与EKF算法、UKF算法及CKF算法相比,MKF算法也保持了KF算法的结构,不同的是在对均值及协方差矩阵的估计上。

2.2 IMM-MKF算法流程

令k-1时刻第i个模型的模型概率为状态估计为状态估计协方差矩阵为,则从k时刻起IM M-MKF算法的计算流程为:

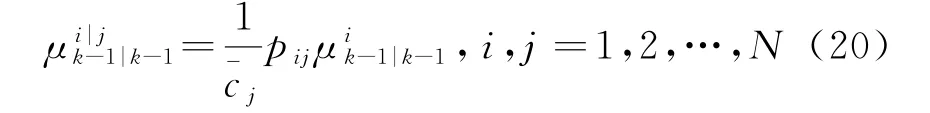
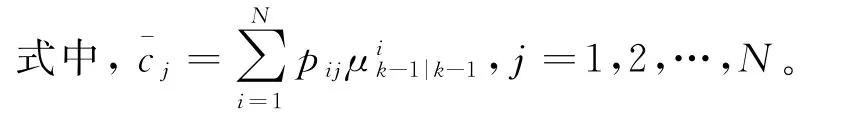
2)对k-1时刻状态及其协方差估计的混合。k-1时刻与第j个模型匹配的MKF算法的混合初始估计为

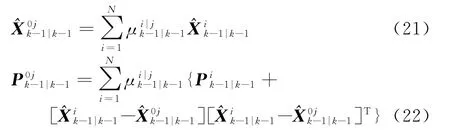
3)滤波。k时刻得到观测量z k后,将和作为此时与第j个模型匹配的MKF算法的输入,进行滤波得到k时刻状态估计及其协方差估计计算模型似然概率

式中,c为归一化常数,且

5)状态及协方差融合估计。按模型概率对N个模型输出的状态估计进行加权可得k时刻对目标的状态估计为

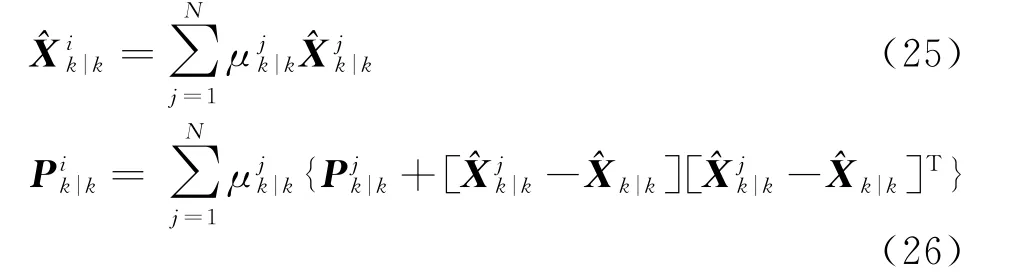
需要注意的是,步骤5)只是输出最终结果,不参与IMM算法的递推过程。

3 算法仿真

以三机只测角跟踪为例对IMM-MKF算法的性能进行仿真分析。3架飞机作匀速直线运动且初始状态分别为(-15 km,0 km,0 m/s,300 m/s)、(0 km,0 km,0 m/s,300 m/s)和(15 km,0 km,0 m/s,300 m/s)。目标机动,初始状态为(60 km,80 km,-200 m/s,-100 m/s),前90 s作带有加速度扰动的匀速直线运动,加速度扰动噪声标准差91～120 s作转弯率为-0.1 rad/s的匀转弯运动,加速度扰动噪声标准差121～200 s重作带有加速度扰动的匀速直线运动。三机测角标准差相同,都为0.5°;观测时间间隔Ts=1s,连续观测200s;两个模型的初始模型概率相等,即μ1=μ2=0.5,模型概率转移矩阵各算法初始化都假设目标相对第一个观测站的径向距离在0～400 km内服从均匀分布,目标沿x轴和y轴的速度分量在-500～500 m/s内服从均匀分布,结合第一个观测站初始时刻角度测量值及均匀分布的统计特性可得目标的初始状态估计。对各算法200次蒙特卡洛实验结果进行统计可得位置RMSE及模型概率估计(以模型2为例)如图1和图2所示。

从图1和图2可以看出,将IMM结构和MKF算法结合的思想是有效的。图1中尽管各种算法跟踪性能趋于一致,但IMM-MKF算法收敛速度快,在跟踪初期就具有很高的跟踪精度,从而能为指挥员提供快速、高精度的目标指示结果。从图1还可以看出IMM-MKF算法在跟踪初期就很平稳,说明MKF算法对模型交互的稳定性。此外,从图2可以看出IMM-MKF算法能够更准确地估计出模型的概率。

需要说明的是,尽管推导过程复杂,MKF算法的最终形式很简洁,很多矩阵可以事先计算并存储,计算量较小,便于工程实现。

4 结束语

本文将边缘化变换(MT)引入状态更新过程,提出了新的跟踪算法即MKF算法,并将其与交互式多模型结合,提出了用于跟踪机动目标的IMMMKF算法。仿真结果表明,上述改进思想是有效的,在本文的仿真场景中取得了比已有典型IMM算法更好的跟踪性能,为解决机动目标的稳健跟踪提供了新的解决思路。

图1 不同机动目标跟踪算法性能比较图

图2 模型估计概率示意图

[2]苏峰,王昌海,徐征.基于最小二乘的时差定位算法[J].雷达科学与技术,2013,11(6):621-625,632.SU Feng,WANG Chang-hai,XU Zheng.TDOA Location Algorithms Based on the Least Squares[J].Radar Science and Technology,2013,11(6):621-625,632.(in Chinese)

[3]陈玲,李少洪.基于无源时差定位系统的机动目标跟踪算法[J].系统工程与电子技术,2005,27(1):127-130.

[4]焦淑红,刘申建,司锡才.机动目标时差无源定位自适应滤波算法研究[J].哈尔滨工程大学学报,2001,22(5):57-61.

[5]宋骊平,姬红兵,高新波.多站测角的机动目标最小二乘自适应跟踪算法[J].电子与信息学报,2005,27(5):793-796.

[6]徐本连,王执铨.一种新的双基阵纯方位机动目标跟踪算法[J].南京理工大学学报,2006,30(2):142-146.

[7]FENG D W,LI T,HUANG Z T.Square-Root Second-Order Extended Kalman Filter and Its Application in Target Motion Analysis[J].IET Radar,Sonar&Navigation,2010,4(3):329-335.

[8]ZHAN R H,WAN J W.Iterated Unscented Kalman Filter for Passive Target Tracking[J].IEEE Trans on Aerospace and Electronic Systems,2007,43(3):1155-1163.

[9]DUNÍK J,ˇSIMANDL M,STRAKA O.Unscented Kalman Filter:Aspects and Adaptive Setting of Scaling Parameter[J].IEEE Trans on Automatic Control,2012,57(9):2411-2416.

[10]ARASARATNAM I,HAYKIN S.Cubature Kalman Filters[J].IEEE Trans on Automatic Control,2009,54(6):1254-1269.

[11]RISTIC B,ARULAMPALAM S,GORDON N.Beyond the Kalman Filter:Particle Filters for Tracking Applications[M].London:Artech House,2004.

[12]SANDBLOM F,SVENSSON L.Moment Estimation Using a Marginalized Transformation[J].IEEE Trans on Signal Processing,2012,60(12):6138-6150.

[13]JULIER S J.The Scaled Unscented Transformation[C]∥Proceedings of the American Control Conference,[S.l]:[s.n.],2002:4555-4559.