面向区域土壤碳通量估算的多向插值空间采样策略
2015-01-19侯建花周国模王国英莫路锋
侯建花, 周国模, 王国英, 莫路锋
1 浙江农林大学环境与资源学院, 浙江省森林生态系统碳循环与固碳减排重点实验室, 临安 311300 2 浙江省景宁县林业局, 景宁 323500 3 浙江农林大学信息工程学院, 临安 311300 4 西安交通大学电子与信息工程学院, 西安 710049
面向区域土壤碳通量估算的多向插值空间采样策略
侯建花1,2, 周国模1,*, 王国英3,4, 莫路锋1,3
1 浙江农林大学环境与资源学院, 浙江省森林生态系统碳循环与固碳减排重点实验室, 临安 311300 2 浙江省景宁县林业局, 景宁 323500 3 浙江农林大学信息工程学院, 临安 311300 4 西安交通大学电子与信息工程学院, 西安 710049
区域土壤碳通量的准确测量对陆地生态系统碳循环过程分析具有十分重要的作用。由于土壤碳通量空间异质性强,采用随机抽样的方法无法对区域土壤碳通量进行准确估算,而大范围的多点采样则需要大量的人力及设备成本。基于一种自制的仪器,提出了一种递增式采样的多向插值采样策略(MDI Multiple Directional Interpolation):在设定初始采样点的基础上,通过对已有采样点的测量,通过径向插值的方法计算采样点连线交点,将不同径向计算值差异最大的点作为新增采样点,以此逐步增加。通过对20 幅的50×50 网格区域仿真,结果表明(1)MDI布局策略能够针对土壤碳通量的变化情况而反馈采样点的疏密。(2)误差分析得出采样点数量(n=10)较少, MDI布局策略对碳通量的估算误差比随机布局策略低, 比平均布局策略稍高;随采样点增多,3种布局策略误差均降低;采样点数量n=40, MDI布局策略对碳通量的估算误差(0.028)比平均布局策略的误差(0.32)降低了12.5%,比随机布局策略的误差(0.04)降低了30.0%。MDI布局策略根据土壤碳通量的变化梯度合理分配采样点,降低区域土壤碳通量监测误差。
多向插值; MDI采样策略; 土壤碳通量估算
土壤碳通量是陆地生态系统碳循环中的重要组成部分[1],它所释放的CO2量约占大气CO2总量的10%—20%,与植被冠层光合作用固碳量相当[2-3]。准确的测量区域土壤碳通量对研究陆地生态系统碳循环过程具有十分重要的作用[4]。现阶段遥感和模型相结合是研究区域碳收支的重要手段,但结果不确定性较大,需要采用通量实测、模型和遥感数据融合的方法来提高模型结果的可靠性[5-8]。直接测定土壤碳通量能够保证区域土壤碳通量的精确性。对土壤碳通量的主要测量方法为开路式的通量测定,对于单点的测量目前认为最准确的是利用LI-8100仪器进行测量。但是由于LI-8100等土壤碳通量测量仪器昂贵,在长期持续的测量过程需要耗费大量人力,同时监测点的时间同步性也很难做到一致,因此通过简单增加监测点的方法进行区域土壤碳通量的监测显得十分困难。无线传感网具有成本低、覆盖范围广、多点同步、持续监测的优点,可应用于大范围的区域监测,作为一种新兴手段已应用在土壤碳通量的直接测定中[2],其相对误差已小于5%。
土壤属性空间分布随地形、气候和植被等因素的变化而不同[9],是一个复杂、变化且不均一的连续体[10],具有明显的空间异质性[11]。少量监测点的均值不能代表整个区域的土壤碳通量,对区域土壤通量的估算有很大的误差。但是监测点数量过多产生能源、财力消耗和数据冗余等问题。因此如何通过尽量少的采样点对土壤碳通量进行测量以得到较准确的区域土壤碳通量值,急需选择一种合理的采样策略满足传感器布置的要求。目前国内外常用的采样方法主要有主观判断采样、简单随机采样、规则网格采样、分区采样及混合采样等[12]。测量区域碳通量普遍运用规则网格或随机的采样方式布设测量点,然后通过简单的统计方法计算区域碳通量。刘源月等人[1,13-15]在研究森林生态系统土壤碳通量过程中,使用简单随机采样方法将测量数据的均值作为区域土壤碳通量。这种方法不能准确、全面地掌握土壤碳通量的空间分布信息[12]。
本文基于一种自制的仪器Lr100GE-6400,通过区域土壤碳通量空间分布仿真数据,提出了一种选择性递增的采样方法多向插值布局策略(MDI),主要研究以下两个方面:(1)MDI采样策略的原理和采样过程;(2)MDI采样策略相对随机采样、均匀采样的优势。通过尽量少的采样点对土壤碳通量进行测量以得到较准确的区域土壤碳通量值。
1 基于多向插值的空间采样策略
在MDI布局策略中,根据已测量采样点的位置及测量值形成交点,计算监测区域中各交点在多个方向上的插值预测结果,选择离散度高的交点进行逐步增设采样点。其中方向指监测点的连线。而交点的离散度是各个方向上插值的方差。它代表了该点在各个方向插值的差异,离散度越大差异越大。因此根据离散度来确定采样点的方式在一定程度上考虑了土壤碳通量空间异质性。
基于多向插值离散度的空间采样布局策略MDI步骤为:首先在研究区域选择若干初始采样点;然后依据空间插值离散度逐步增加采样点。具体描述如下:
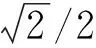
(2) 产生交点 监测区域内已布设的监测点相互连接形成多条连线,连线相交形成交点。根据王丰川等[17]研究得到土壤碳通量的最近采样距离为20 m,在20 m内土壤碳通量的变化梯度很小,所以交点距离小于阈值ε(ε=20 m)时,近似认为它们交于同一个公共交点。如图2所示,假设已在5个位置部署了采样点,已部署采样点在监测区域内形成8个交点。
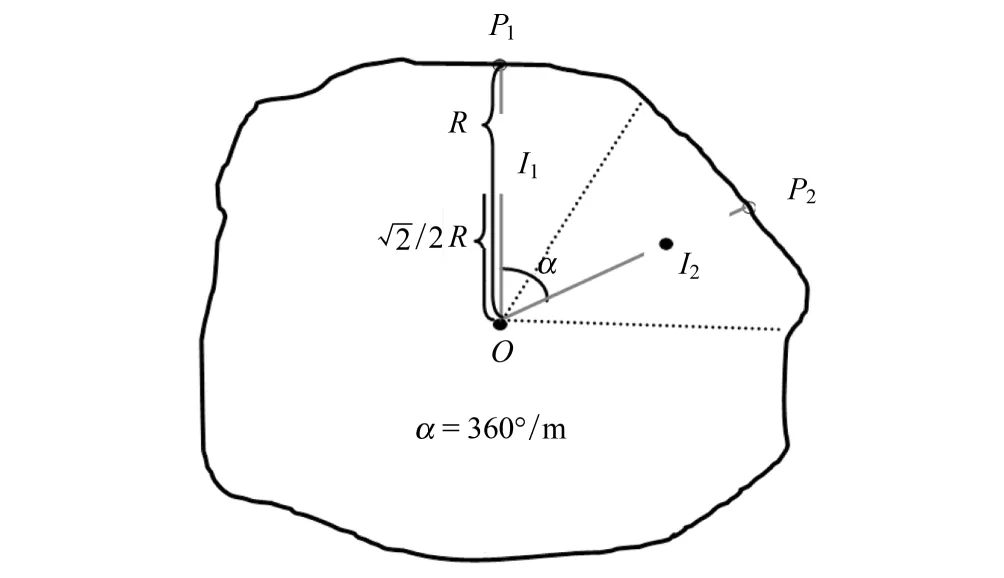
图1 初始点的生成示意图Fig.1 Generation of initial points

图2 采样点的生成Fig.2 Generation of sampling points
(3) 计算多向插值离散度 根据已测量的各采样点的土壤碳通量数据,对各个方向的交点位置进行插值估算,计算各交点的多向插值离散度。
高东等[16]对区域土壤碳通量的研究表明,土壤碳通量在空间上是连续变化的,因此在各个方向上可以通过插值方法估算未知点的碳通量。如图3单向插值所示, A1、B1为区域中的两个采样点,已知A1和B1点的土壤碳通量分别为fluxΑ1和fluxB1,可以通过A1和B1点运用插值方法来估算得到C点的土壤碳通量值fluxc,如式(1)所示,其中X是对应点的相对横坐标。
(1)
采样点在监测区域中相互交叉形成多个方向,未测量交点的土壤碳通量根据多个方向的插值可以得到多个估算结果。如图3多向插值所示,A1、B1、A2、B2、…、An、Bn为已进行测量的位置,这些位置分别构成L1、L2、…、Ln等多个方向,C点为多个方向的交点。则未测量交点C在L1、L2、…、Ln各方向上分别得到不同预测值fluxL1、fluxL2、…、fluxLn。计算出交点上预测值的离散度,选择离散度高的点进行采样,通过该点的实际数据修正通量值提升各方向估值精度,使整个区域土壤碳通量的估算更准确。多向插值离散度δ计算方法为(式2):
(2)
(4) 选择新增采样点 监测区域内已布设的监测点形成多个方向,各个方向之间相交形成交点,从所有交点中选择多向插值离散度最高的点作为新增采样点。
重复步骤(2)、(3)和(4),直到各交点的多向插值离散度均低于设定阈值为止。
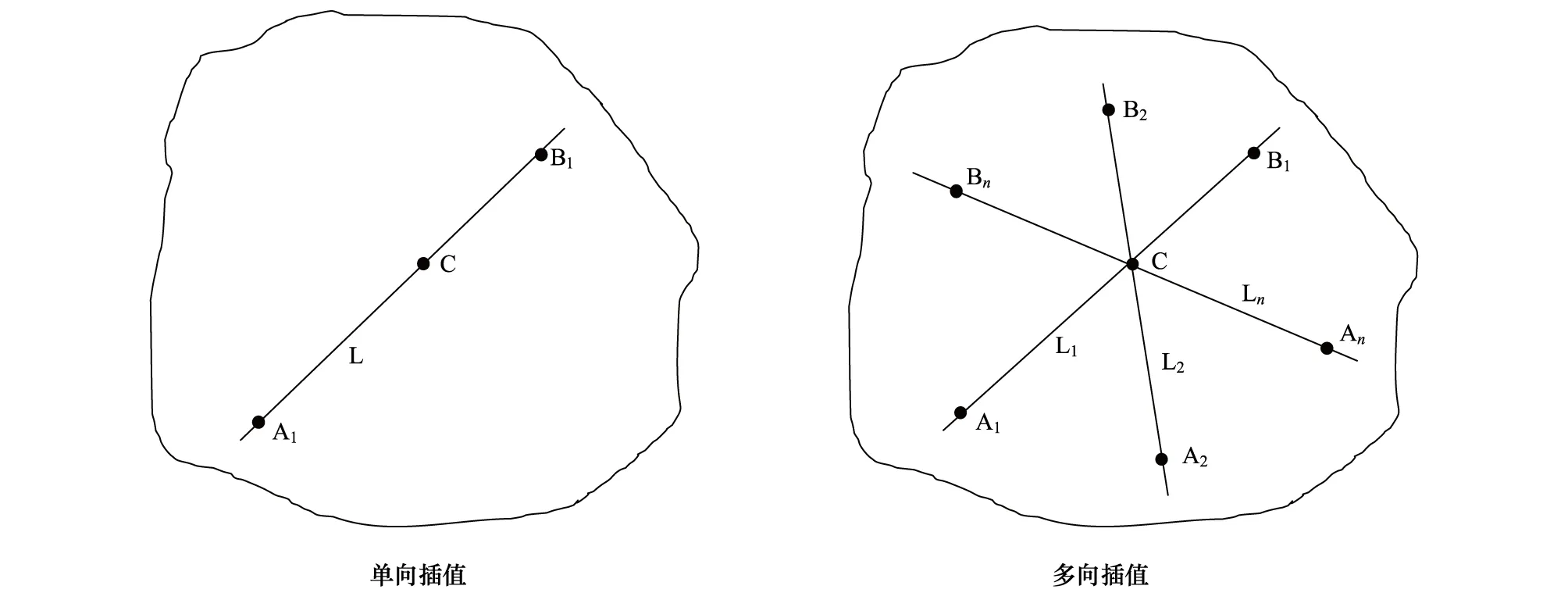
图3 多向插值离散度Fig.3 Dispersion of multiple directional interpolations
2 模拟实验与分析
通过模拟区域土壤碳通量数据,利用MDI空间采样布局策略进行20 次仿真实验,并对实验结果进行分析。
2.1 实验数据
根据张义辉等统计出的区域土壤碳通量空间布局结果[18],设定模拟区域土壤碳通量数据的特征(表1)。模拟实验区域为1 km×1 km,分割成50 m×50 m的方格矩阵,在每个方格内赋予土壤碳通量值,矩阵行列下标(x,y)表示对应模拟区域的位置,1≤x,y≤50。

表1 实验数据参数
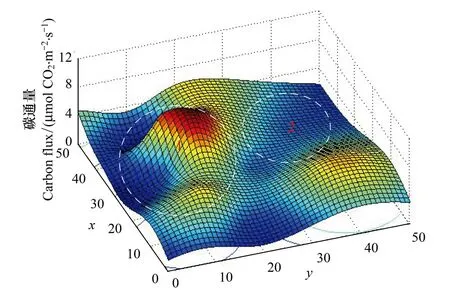
图4 土壤碳通量模拟图Fig.4 Simulation map of soil carbon flux
为了保证实验模拟数据的代表性,实验按照表1的规范模拟产生20幅不同的区域土壤碳通量分布数据,作为实验数据。图4为其中一幅符合空间分布特征(平均值为3.56,标准差为2.54,变程为210, 块金值为0.81,变异系数为45)的1 km×1 km区域土壤碳通量空间分布模拟图。在圆形范围1附近,土壤的碳通量值变化梯度相对较大;在圆形范围2附近,土壤的碳通量值变化梯度相对较小。
2.2 实验方案
在仿真试验中,采样点位置用模拟数据的坐标表示,采样点的测量值用该位置的土壤碳通量仿真值表示。使用传统和地统计学的方法对土壤碳通量的空间分布进行比较,运用地统计学Kriging插值方法能更准确地展现土壤碳通量的空间分布[12]。通过将采样点的Kriging空间插值结果与整个区域的仿真值进行对比,评价部署策略的性能。实验对传统的主观判断采样方法、分区和混合采样和MDI布局策略3采样方法进行了比较。
基于20幅区域土壤碳通量分布的模拟数据,分别运用MDI布局、随机布局和均匀布局策略,进行布设测量点。采样点数量分别为区域土壤碳通量总数的0.4%、0.8%、1.2%、1.6%的,即采样点数量n=10, 20, 30, 40(图5)。在采样点数量相同的条件下,比较MDI布局策略与随机布局策略、均匀布局策略对区域土壤碳通量的估算效果。
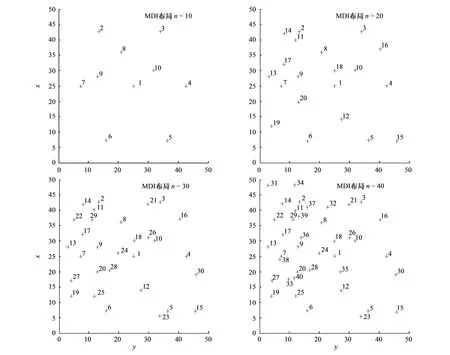
图5 MDI (Multiple Directional Interpolation)测量点布局Fig.5 MDI distribution of sampling points
2.3 实验结果
通过对20幅土壤碳通量空间模拟数据的布点实验结果进行统计,得出MDI布局策略与随机布局策略、均匀布局策略的区域碳通量估算误差(图6)以及MDI布局策略与随机布局策略、均匀布局策略的估算误差的标准差(图7)。通过分析得出:
(1) 3种布局策略的误差和误差标准差与测量点的数量的关系整体趋势是相同的:测量点数量越多,误差和误差标准差减小,趋势逐渐变缓。
(2) 在相同的测量点数量n(n=10, 20, 30, 40)下,随机布局策略的误差和误差标准差均比MDI布局策略的大。采样点数量(n=40)时,MDI布局策略对碳通量的估算误差(0.04)比随机布局策略的估算误差(0.028)低30.0%。MDI布局策略和随机布局策略的误差差异极显著(P<0.01)(图6),MDI布局策略明显优于随机布局策略。
(3) 在测量点数量n=10时,均匀布局策略的误差和误差标准差比MDI布局策略的低;随着测量点数量n(n= 20, 30, 40)增大,均匀布局策略的误差和误差标准差比MDI布局策略的大。采样点数量(n=40)时,MDI布局策略对碳通量的估算误差(0.028)比平均布局策略的误差(0.32)低12.5%。MDI布局策略和均匀布局策略的误差差异极显著(P<0.01)(图6),增加测量点数量后,MDI布局策略明显优于均匀布局策略。

图6 碳通量估算误差Fig.6 Estimation error of carbon flux

图7 碳通量估算误差的标准差Fig.7 Standard deviation of carbon flux estimation error
2.4 实验分析
对MDI布局策略的估算效果优于均匀和随机布局的原因进行分析,图8是对应模拟区域中土壤碳通量采样结果。测量点n=40时,MDI布局策略的估算误差与随机布局策略、均匀布局策略(图9)的误差对比得出,对应区域土壤碳通量分布(图4)范围1中,均匀布设策略和随机布设策略误差比MDI布设策略的估算误差高;对于范围2, MDI布局策略比其它两种的估算误差略高。均匀和随机两种布局策略在范围1中的较大的估算误差导致最终估算误差及误差标准差较大。
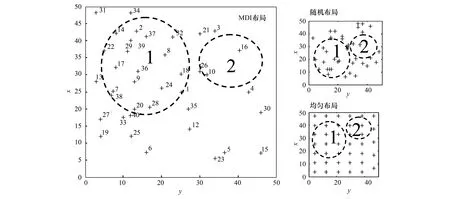
图8 MDI与随机方法、均匀方法的采样点分布对比(n=40)Fig.8 Contrast between MDI and random & uniform sampling points distribution
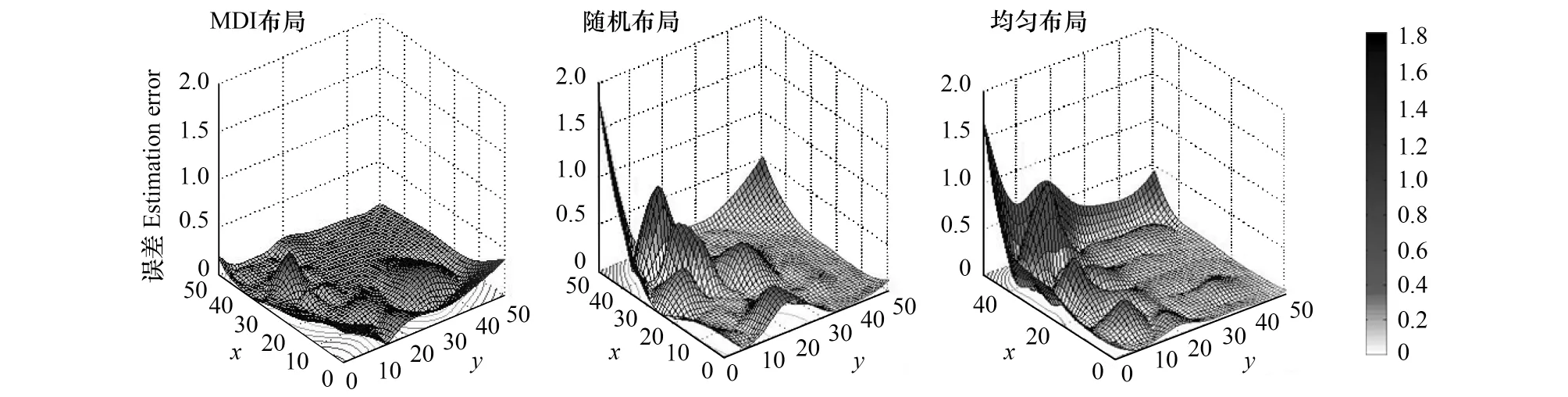
图9 MDI与随机方法、均匀方法的误差分布对比Fig.9 Contrast between MDI and random & uniform distribution of error
局部测量点密度(表2)是导致误差分布不同的原因。在土壤碳通量变化较复杂的范围1处,较多测量点能够准确地得到该区域土壤碳通量的变化趋势,而测量点不足是导致该区域土壤碳通量的变化趋势不精确的原因。

表2 MDI(Multiple Directional Interpolation)与随机方法、均匀方法的采样点数量分布对比
对应图4中范围1的区域,将图8采样分布和图9误差分布进行对应分析,MDI中测量点比较密集,高达21个(表2);但是随机布局策略和均匀布局策略(图8)相对MDI的测量点布局要稀疏许多,测量点数量分别为16个和10个,尤其是随机布设的测量点随意性较大,导致此区域的测量点不足。而对应图5中范围2处,MDI的布点比较稀疏,仅有2个(表2);但是随机布局策略和均匀布局策略相对MDI的布设要密集,其测量点数量均为5个。可见,MDI布局测量能够根据土壤碳通量的变化梯度合理分配测量点。
3 结论
本文针对区域土壤碳通量估算的采样点布局问题提出了MDI空间采样布局策略。使用MDI布局策略进行模拟实验,验证了MDI布局比均匀布局和随机布局能够得到更高的估算精度。对实验结果的误差进行比较,采样点数量(n=10)较少, MDI布局策略对碳通量的估算误差比随机布局策略低, 比平均布局策略稍高;随测量点增多,3种布局策略误差均降低;采样点数量(n=40)增多时, MDI布局策略对碳通量的估算误差(0.028)比平均布局策略的误差(0.32)低12.5%,比随机布局策略的误差(0.04)低30.0%。综合比较3种布局方法, MDI布局策略从整体上对测量点数量进行了合理的分配,使得整个区域内误差低。MDI部署策略在土壤碳通量变化梯度大的区域设置较多采样点,能够更好的拟合出此区域土壤碳通量的变化,很大程度上降低了误差;在土壤碳通量变化梯度小的区域,MDI布局策略设置较少的采样点,但对土壤碳通量的估算准确度影响不大。通过实验得到MDI的布局策略使每个采样点的作用最大化。
在真实条件下最佳(多向插值离散度最大)位置并不适合部署土壤测量设备(例如水池、石头等非土壤表面)。此时,可以考虑采用两种措施:依据土壤碳通量的局部相关性,选择理论最佳部署位置周边作为新增采样点;或者在多向插值离散度相差不大的情况下,选用离散度相对较大的其它位置作为新增采样点。但无论哪种方法都降低了MDI布局策略的性能,并且在理论最佳位置附近仍然不适合部署节点,最佳位置的多向插值离散度与其余交点的多向插值离散度接近时,不容易确定新增采样点位置。下一步工作要进行包含大面积非土壤表面的区域土壤碳通量空间采样策略研究。
[1] 刘源月, 江洪, 邱忠平, 原焕英, 李雅红. 亚热带典型森林生态系统土壤呼吸. 西南交通大学学报, 2009, 44(4): 590-594.
[2] 徐林, 莫路锋, 宣子蔚, 徐小军, 王圣辉, 周国模. 基于WSN的土壤碳通量测量系统. 林业科学, 2013, 49(2): 122-126.
[3] Raich J W, Schlesinger W H. The global carbon dioxide flux in soil respiration and its relationship to vegetation and climate. Tellus, 1992, 44(2): 81-99.
[4] Fang C, Moncrieff J B, Gholz H L, Clark K L. Soil CO2efflux and its spatial variation in a florida slash pine plantation. Plant and Soil, 1998, 205(2): 135-146.
[5] 米娜, 于贵瑞, 王盘兴, 温学发, 孙晓敏, 张雷明, 宋霞, 王树森. 基于EALCO模型对中亚热带人工针叶林CO2通量季节变异的模拟. 植物生态学报, 2007, 31(6): 1119-1131.
[6] Zhou L, Wang S Q, Ju W M, Xiong Z, Georg K, Chen J M, Shi H. Assessment of carbon dynamics of forest ecosystems in the Poyang lake basin responding to afforestation and future climate change. Journal of Resources and Ecology, 2013, 4(1): 11-19.
[7] Tate K R, Scott N A, Parshotam A, Brown L, Wilde R H, Giltrap D J, Trustrum N A, Gomez B, Ross D J. A multi-scale analysis of a terrestrial carbon budget: is New Zealand a source or sink of carbon. Agriculture, Ecosystems and Environment, 2000, 82(1/3): 229-246.
[8] Potter C S, Klooster S A, de Carvalho C R, Genovese V B, Torregrosa A, Dungan J, Bobo M, Coughlan J. Modeling seasonal and interannual variability in ecosystem carbon cycling for the Brazilian Amazon region. Journal of Geophysical Research, 2001, 106(D10): 10423-10446.
[9] 魏书精, 罗碧珍, 孙龙, 魏书威, 刘芳芳, 胡海清. 森林生态系统土壤呼吸时空异质性及影响因子研究进展. 生态环境学报, 2013, 22(4): 689-704.
[10] Huggett R J. Soil chronosequences, soil development, and soil evolution: a critical review. Catena, 1998, 32(3/4): 155-172.
[11] 周涛, 史培军, 惠大丰, 骆亦其. 中国土壤呼吸温度敏感性空间格局的反演. 中国科学C辑: 生命科学, 2009, 39(3): 315-322.
[12] 陈天恩, 陈立平, 王彦集, 郜允兵, 任仲山. 基于地统计的土壤养分采样布局优化. 农业工程学报, 2009, 25(增2): 49-55.
[13] 王超, 黄蓉, 杨智杰, 刘强, 陈光水, 万晓华. 万木林保护区柑橘和锥栗园土壤呼吸的比较. 应用生态学报, 2012, 23(6): 1469-1475.
[14] 常宗强, 冯起, 司建华, 李建林, 苏永红. 祁连山不同植被类型土壤碳贮量和碳通量. 生态学杂志, 2008, 27(5): 681-688.
[15] 周文嘉, 石兆勇, 王娓. 中国东部亚热带森林土壤呼吸的时空格局. 植物生态学报, 2011, 35(7): 731-740.
[16] 高东, 鲁绍伟, 绕良懿, 李佳, 张滕, 靳阿亮. 淮北平原四种土地利用类型非生长季土壤呼吸速率. 农业工程学报, 2011, 27(4): 94-99.
[17] 王丰川, 刘加珍, 陈永金. 黄河三角洲湿地土壤呼吸及其环境因子分析. 人民黄河, 2013, 35(1): 81-84.
[18] 张义辉, 李洪建, 荣燕美, 严俊霞, 李君剑. 太原盆地土壤呼吸的空间异质性. 生态学报, 2010, 30(23): 6606-6612.
Spatial sampling layout strategy for regional soil carbon flux estimation based on multiple directional interpolation
HOU Jianhua1,2, ZHOU Guomo1,*, WANG Guoying3,4, MO Lufeng1,3
1ZhejiangProvincialKeyLaboratoryofCarbonCyclinginForestEcosystemsandCarbonSequestration,SchoolofEnvironmentalandResourceSciences,ZhejiangAgricultureandForestryUniversity,Lin′an311300,China2JingningForestryBureau,Jingning323500,China3SchoolofInformationEngineering,ZhejiangAgricultureandForestryUniversity,Lin′an311300,China4SchoolofElectronicandInformationEngineering,Xi′anJiaoTongUniversity,Xi′an710049,China
Soil carbon flux is a vital part of the terrestrial ecosystem carbon cycle. Carbon dioxide released from soil is 10% to 20% of the total amount of that in atmosphere, equal to carbon assimilation by photosynthesis in plant canopies. Thus accurate measurement of regional soil carbon flux is significant for research on carbon cycling in terrestrial ecosystems. Remote data combined with models to analyze regional carbon balance is important but unreliable. The data from direct measurement of soil carbon flux turns to be more accurate. During the measuring process, random sampling results in inaccurate estimates of the regional soil carbon flux because of strong spatial heterogeneity. Another method, multi-point sampling in a wide area, requires much more human labor and equipment costs. However, a wireless sensor net (WSN) is a new method that has been applied to the measurement of soil carbon flux. Its advantages are low expense, wide coverage, multi-point synchronization, continuous monitoring, and be applicability to a wide range of areas. By using a self-regulating instrument based on WSN, Lr100GE-6400, to measure regional soil carbon flux, this paper presents a new layout strategy, Multiple Directional Interpolation (MDI). The strategy is as follows: (a) Set up the original well-distributed sampling sites and measure the carbon flux of these sites. (b) Calculate the intersections of different connection lines between sampling points by the radial point interpolation method and regard the points with maximum radial differences as new sampling points. Consequently, points are gradually increased based on this method to achieve accurate estimates of regional soil carbon flux. MDI layout strategy considers the spatial heterogeneity of soil carbon flux. It determines the sampling points based on dispersion, so that MDI can provide more accurate and comprehensive spatial information. Based on simulations in 20 fields of the 50×50 mesh region, layout is set up by MDI, random layout strategy, and uniform layout strategy, respectively. Keeping the same sample points, the three strategies were compared, and results were as follows: (1) MDI layout strategy can reflect the density of sampling points in terms of the variation gradient of soil carbon flux, decreasing use of sampling points and increasing the accuracy of measurement. (2) Error analysis of the experiments verified that the MDI layout strategy is more accurate than the average and random layout strategies. If there are fewer sampling points (n=10), errors in the MDI layout strategy are less than the random and more than the average strategies; if sampling points increase, the three types of layout strategies tend to be more accurate. If there are 40 sampling points, errors in MDI (0.028) are 12.5% less than that of the average (0.32),and 30.0% less than that of the random strategy. In conclusion, MDI layout strategy generally allocates the sampling points more reasonably based on the variation gradient of soil carbon flux. More sampling points are selected in the region with a large variation gradient in soil carbon flux, which matches the variation of soil carbon flux accurately, while fewer are located in the region with a small variation gradient in soil carbon flux but these do not affect the accuracy of soil carbon flux measurement. This method maximizes the effect of every sampling point and minimizes errors.
multiple-directional Interpolation; MDI layout strategy; soil carbon flux estimation
国家自然科学基金重大项目(61190114/F0102); 国家自然科学基金(61303236); 国家林业局948项目(2013-4-71);浙江省科技计划项目重大科技专项(2012C13011-1); 景宁畲族自治县科技计划项目(2014A05-5)
2014-01-29;
日期:2014-11-19
10.5846/stxb201401290209
*通讯作者Corresponding author.E-mail: zhougm@zafu.edu.cn
侯建花, 周国模, 王国英, 莫路锋.面向区域土壤碳通量估算的多向插值空间采样策略.生态学报,2015,35(18):6070-6077.
Hou J H, Zhou G M, Wang G Y, Mo L F.Spatial sampling layout strategy for regional soil carbon flux estimation based on multiple directional interpolation.Acta Ecologica Sinica,2015,35(18):6070-6077.
