模态耦合及摩擦系数 速度斜率与黏滑运动的关系
2015-01-19张立军孟德建
张立军,吴 军,孟德建
(同济大学汽车学院,上海201804)
模态耦合及摩擦系数 速度斜率与黏滑运动的关系
张立军,吴 军,孟德建
(同济大学汽车学院,上海201804)
摩擦尖叫的理论目前主要有摩擦系数 速度负斜率、模态耦合、黏 滑运动和锁 滑理论,但没有一种理论可以完全解释摩擦尖叫等现象.因此,深入探讨各个理论之间的内在联系对于统一摩擦振动和噪声机理的认识至关重要.以摩擦系数及其速度特性为切入点,基于考虑摩擦系数及其速度斜率的单点接触集总参数柔体 刚体组成的二自由度非线性摩擦振动动力学模型,通过理论推导和数值计算研究摩擦系数 速度斜率对模态耦合不稳定的影响,并根据摩擦系数及其速度斜率的符号形成4个区域,分析了4个区域的黏 滑运动的特点和极限环及工况依赖性,并指出在摩擦系数 速度正斜率情况下系统参数改变会导致Hopf分岔.
摩擦尖叫;摩擦系数 速度斜率;模态耦合;黏滑运动;Hopf分岔
摩擦振动和噪声现象广泛存在于各种机械摩擦系统中,例如制动器、离合器和列车轮轨系统等[1-2].迄今为止,人们尚未完全弄清摩擦振动和噪声的发生机理,亦未建立完全行之有效的控制方法.因此,它一直是学术界和工业界的关注热点[1-4].
截至目前,有关摩擦振动和噪声的发生机理理论主要包括黏滑运动理论、摩擦系数 速度负斜率理论、模态耦合不稳定理论、自锁 滑动理论以及摩擦激励与结构耦合统一理论等,详见多篇综述性论文[1-2,528].其中,模态耦合不稳定理论不仅能够解释许多摩擦噪声现象,而且便于利用有限元软件进行面向对象的预测与分析,应用非常广泛[1-4].黏滑运动[29-32]作为最早提出的一种摩擦噪声机理理论,常被看作是低声压级摩擦尖叫发生的主要原因.摩擦系数 速度负斜率不稳定理论[30-31,33-34]是一个曾经被广泛认可的理论,但因为不能合理解释摩擦噪声对摩擦系数的依赖性以及不存在负斜率时仍发生噪声等现象而受到严重质疑,认可度下降.回顾历史发现,不同的机理理论由不同的研究者在不同的时期针对不同的对象采用不同的研究手段得到,因此研究者们似乎都会“过度”专注于自己提出的理论,试图解释所有的摩擦振动和噪声现象,同时,又严重忽视了对所提出理论成立条件的严格界定,更缺乏与其他理论之间的相互联系的研究.这也许就是目前尚未对摩擦振动和噪声机理形成共识的原因所在.
众所周知,摩擦特性对于摩擦振动和噪声具有极其重要的影响,在各种机理理论中,摩擦特性都占据着极其重要的地位.摩擦特性,不仅包括摩擦系数的大小,也包括摩擦系数 速度斜率.因此,摩擦特性无疑成为探究不同摩擦振动和噪声机理理论之间联系的极好切入点.在此背景下,本文从摩擦特性(摩擦系数及其速度斜率)切入,针对一类由集总参数柔体 刚体摩擦副构成的摩擦振动系统建立点接触摩擦振动动力学模型,采用数学公式推导和数值计算的手段考察不同摩擦系数和摩擦系数 速度斜率组合条件下的系统摩擦振动不稳定性,以及黏滑动态响应现象的异同,探讨模态耦合、负斜率和黏滑运动3种理论之间的联系.
1 摩擦系统的模态耦合不稳定性
1.1 摩擦振动物理模型
借鉴文献[6],针对一类典型的由集总参数柔体和刚体摩擦副构成的摩擦振动系统建立单点接触、单质量二自由度非线性动力学模型,如图1所示.图1中,集总参数柔体由具有x和y 2个自由度的质点质量m,与x轴成和角度的刚度分别为k1和k2的弹簧构成.刚体为按照速度v0平移的无质量刚性带.柔体和刚体之间为单点接触,法向接触刚度为k3.为了保持二者始终处于摩擦接触状态,在质点上施加法向力L.FN与FF分别表示质点与带之间的法向接触力与摩擦力.

图1 二自由度非线性摩擦振动模型Fig.1 2degrees of freedom nonlinear friction vibration model
1.2 摩擦系数模型
柔体和刚体之间的摩擦系数为f,其数学表达式为

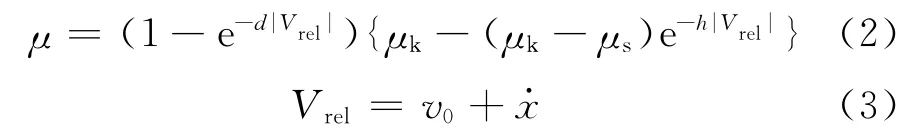
式中:μk,μs分别为动、静摩擦系数的控制参数;d,h分别为原点附近正斜率区的大小与动摩擦区斜率大小的控制参数.Vrel为质点与带之间的相对速度大小.
定义摩擦系数参数组合Ⅰ(μs=0.6,μk=0.4,d=50,h=1)和摩擦系数参数组合Ⅱ(μs=0.4,μk=0.6,d=50,h=1),分别得到具有摩擦系数 速度负斜率和摩擦系数 速度正斜率的摩擦系数特性,用于后续的数值计算分析.其特性曲线如图2所示.

图2 摩擦系数 速度曲线Fig.2Friction coefficient velocity curve
1.3 摩擦系统的动力学模型
系统的动力学方程为
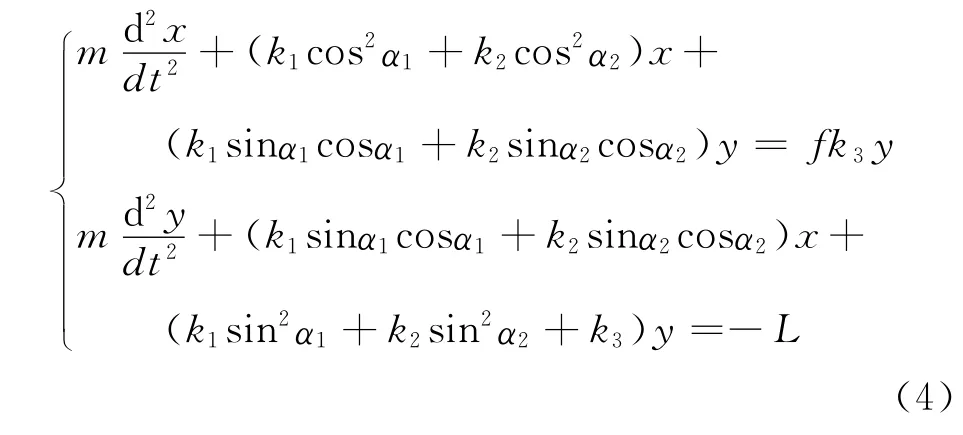

可通过平移变换把平衡点调整到坐标原点,故令式(5)中x=u*+u,y=v*+v,可得
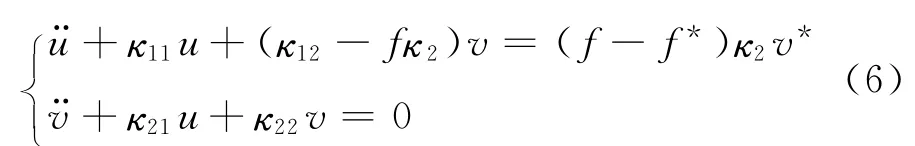
式 中,u*
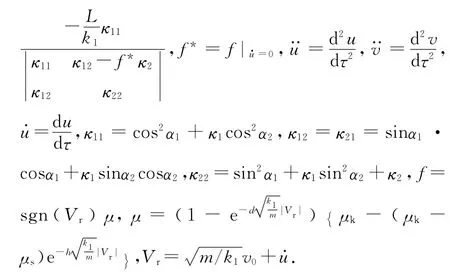
2 摩擦特性对模态耦合不稳定的影响
2.1 系统线性化与稳定性分析
对摩擦系数进行泰勒级数展开,并忽略高次项,可得
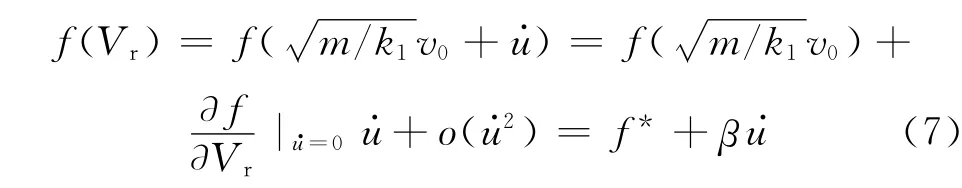
将式(7)代入式(6),只考虑平衡位置附近的振动,故忽略高次项u·v,可得
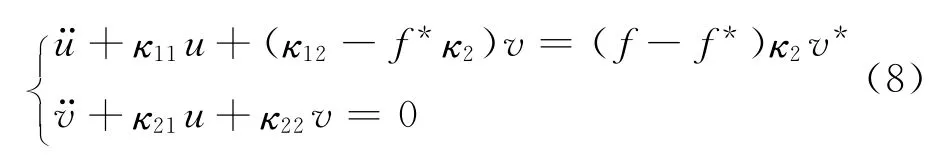
将式(8)写成矩阵形式,可得线性化系统为
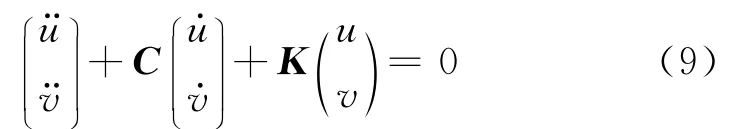
由式(9)可知,由于存在摩擦系数 速度斜率,系统产生了阻尼矩阵C,即在u方向的等效阻尼为-βκ2v*,而在v方向上的等效阻尼为零.
令,其中V为特征向量,λ为特征值,可得线性化系统(9)的特征方程为一个关于λ的一元四次的特征多项式
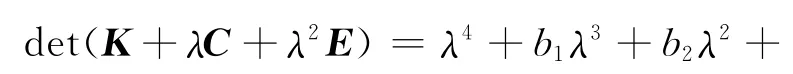

式中:b1=-βκ2v*;b2=κ11+κ22;b3=-βκ2v*κ22;b4=κ11κ22-κ212+f*κ2κ12.
易知,当所有特征值的实部都小于零时,线性化系统(9)稳定;而当至少有1个特征值的实部大于零时,线性化系统(9)不稳定.
分别在β=0,β<0,β>0 3种摩擦系数 速度斜率下,结合摩擦系数的大小,分析摩擦特性对模态耦合不稳定的影响.
2.2 摩擦系数 速度斜率为零情形
可以计算特征值,根据实部的符号变化确定模态耦合不稳定性,进而确定摩擦系数分岔点.
显然,1+κ21+κ22+2κ1cos(2α1-2α2)-2κ2· cos(2α1)-2κ1κ2cos(2α2)>0,因此可以确定:仅当κ12>0,且f*>[1+κ21+κ22+2κ1cos(2α1-2α2)-2κ2cos(2α1)-2κ1κ2cos(2α2)]/[2κ2sin(2α1)+2κ1κ2sin(2α2)]时,系统出现正实部特征值.
当摩擦系数f*较小时,系统具有4个实部为零的特征值,存在2个稳定模态;随着f*的增大,系统出现2个正实部特征值和2个负实部特征值,出现1个不稳定模态和1个稳定模态.由此确定f*的分岔点为:当κ12>0时,分岔点为f*a1=[1+κ21+κ22+2κ1cos(2α1-2α2)-2κ2cos(2α1)-2κ1κ2cos(2α2)]/(2κ2κ12);当κ12<0时,系统无分岔点.
2.3 摩擦系数 速度斜率小于零情形
利用Routh Hurwitz判据[35]进行特征值实部正负号的判断,并可进而根据线性稳定性定理[36]基于线性化系统(9)在平衡点附近的稳定性判断非线性系统(6)的稳定性.由式(10)易知,H1=b1,H2=b1b2-b3,H3=b1b2b3-b23-b4b21,H4=b4H3.
根据Routh Hurwitz判据,假设线性化系统(9)在平衡点处稳定,即Hi(i=1,2,3,4)>0.由H1>0可得v*>0,即κ11(κ11κ22-κ212+f*κ2κ12)<0;由H3>0及H4>0可得κ11κ22-κ212+f*κ2κ12>0.
因κ11>0,H1>0和H3>0不能同时成立.因此,线性化系统(9)在平衡点处不稳定,非线性系统(6)在平衡点处也不稳定.
在式(10)中,令λ′=-λ,由此可得一个关于λ′的一元四次的特征多项式:

由此可得:当κ12>0时,f*<κ12/κ2,或当κ12<0时,f*<(κ11κ22-κ212)/(-κ2κ12)有4个实部小于零的特征值,则λ有4个实部大于零的特征值,线性化系统(9)不稳定.当κ12>0时,f*>κ12/κ2或当κ12<0时,f*>(κ11κ22-κ212)/(-κ2κ12),λ′有2个正实部特征值和2个负实部特征值,则λ有2个负实部特征值和2个正实部特征值,线性化系统(9)不稳定.
当f*较小时,系统具有4个实部大于零的特征值,存在2个不稳定模态;随着f*增大,系统出现2个正实部特征值和2个负实部特征值,出现1个不稳定模态和1个稳定模态.由此确定摩擦系数f*的分岔点为:当κ12>0时,分岔点为fb*1=κ12/κ2;当κ12<0时,分岔点为.
定义系统参数组合Ⅰ(α1=150°,α2=30°,m= 0.5kg,L=7N),对应的κ12≈5.60,即κ12>0,结合摩擦系数参数组合I,保持图2中对应速度下的斜率β值不变,而不断改变f*,对线性化系统(9)计算特征值实部与频率,得到二者在不同的摩擦系数 速度斜率情况下随f*变化的情况,如图3.从图3a和3b分析可知:
(2)当β<0时,无论摩擦系数的大小,系统总是存在正实部的特征值,系统始终不稳定;且随负斜率β绝对值的增大(对应的v0减小),特征值正实部增大,系统不稳定性增强.
(4)摩擦系数 速度有无负斜率以及斜率大小对频率的改变不大(图3b).

图3 β<0时特征值随摩擦系数的变化Fig.3 The locus of eigenvalue with respect to friction coefficient whenβ<0
因此,摩擦系数 速度负斜率会增强系统的不稳定,但不会显著改变不稳定频率的大小;不同负斜率β对应的模态耦合不稳定的摩擦系数分岔点相同,这与理论推导结果一致.
2.4 摩擦系数 速度斜率大于零情形
与前类似,根据Routh Hurwitz判据得到H1,H2,H3,H4.假设Hi(i=1,2,3,4)>0,由H1>0可得v*<0,即κ11(κ11κ22-κ212+f*κ2κ12)>0,而当H1>0时,H2>0恒成立.由H3>0,可得κ212-f*κ2κ12>0.由H4>0可得κ11κ22-κ212+f*κ2κ12>0.即只要满足κ11κ22-κ212+f*κ2κ12>0,κ212-f*κ2κ12>0时,线性化系统(9)稳定.
由此可得,当κ12>0时,f*<κ12/κ2,或当κ12<0时,f*<(κ11κ22-κ212)/(-κ2κ12),有4个实部小于零的特征值,线性化系统(9)稳定.当κ12>0时,f*>κ12/κ2或当κ12<0时,f*>(κ11κ22-κ212/(-κ2κ12),系统有2个正实部特征值和2个负实部特征值,线性化系统(9)不稳定.
当f*较小时,系统具有4个实部小于零的特征值,存在2个稳定模态;随着f*增大,系统出现2个正实部特征值和2个负实部特征值,出现1个不稳定模态和1个稳定模态.由此确定f*的分岔点为:当κ12>0时,分岔点=κ12/κ2;当κ12<0时,分岔点=(κ11κ22-κ212)/(-κ2κ12).
与前类似,利用系统参数组合I,结合摩擦系数组合参数II进行计算,得到二者特征值实部与频率在不同的β情况下随f*变化的情况,如图4.由图4a和4b分析可知:
(4)摩擦系数 速度有无正斜率以及斜率大小对频率的改变不大(图4b).
综上,摩擦系数 速度正斜率会增强系统的稳定性,但不会显著改变不稳定频率的大小;不同正斜率β对应的模态耦合不稳定的摩擦系数分岔点相同,但因fa*1≥fc*1,因此β>0比β=0可以在更宽的摩擦系数范围内产生模态耦合.

图4 β>0时特征值随摩擦系数的变化Fig.4 The locus of eigenvalue with respect to friction coefficient whenβ>0
2.5 摩擦系数和摩擦系数 速度斜率的汇总分析
汇总上述分析,在不同摩擦系数 速度斜率情况下的系统不稳定如表1所示.由表可见:模态耦合的分岔点摩擦系数的大小仅取决于系统的结构参数和接触参数,虽然与摩擦系数 速度斜率的大小无关,但是与摩擦系数 速度斜率的正负紧密相关.当κ12> 0时,;当κ12<0时,β=0时系统始终只有2个稳定模态,因此,β≠0比β=0在摩擦系数的更大范围内产生模态耦合不稳定.

表1 不同斜率时的模态耦合分岔点及模态稳定性Tab.1 The bifurcation point and modal stability with respect to different kinds of slope
参照表1,基于系统参数组合Ⅰ,取f*与β组合随机数进行特征值的计算和稳定性的判断,如图5.按照模态耦合摩擦系数分岔值和摩擦系数 速度斜率将图形分成4个区域:①正斜率无模态耦合稳定区(Ⅰ区);②正斜率模态耦合不稳定区(Ⅱ区);③负斜率无模态耦合不稳定区(Ⅲ区);④负斜率模态耦合不稳定区(Ⅳ区).4个区域之间分界线分别为β=0和(分岔点参数也可能不相等).根据图5可知,摩擦系数 速度负斜率引起的不稳定和模态耦合不稳定是2种完全独立的摩擦振动和噪声发生机理理论,彼此独立且可以并存.
图6所示为对应4个区域的系统特征值实部与频率关系图.由图6可知:①Ⅰ区和Ⅲ区几乎对称,系统分别有2个稳定频率和2个不稳定频率,这是因为摩擦系数相等时,无论β的正负与大小,频率都比较接近;②Ⅱ区与Ⅳ区都有1个不稳定频率和1个稳定频率,2个区域也近似对称分布,原因同前.

图5 摩擦系数及其斜率变化时的4个区域Fig.5 Four areas when friction coefficient and slope change
3 摩擦特性对黏滑运动的影响
按照4个区域系统考察摩擦特性变化对系统黏滑运动的影响以及其对工况的依赖性.
考虑到有时可能存在极限环,首先介绍进行极限环存在性判断的Bendixson Dulac判据[36].
定义X(τ)=(u(τ)w(τ)v(τ)z(τ) )T,将运动微分方程(6)化成状态空间方程,可得
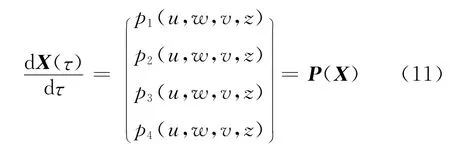

图6 4个区域的频率 实部关系Fig.6 The relationship between frequency and real part in four areas
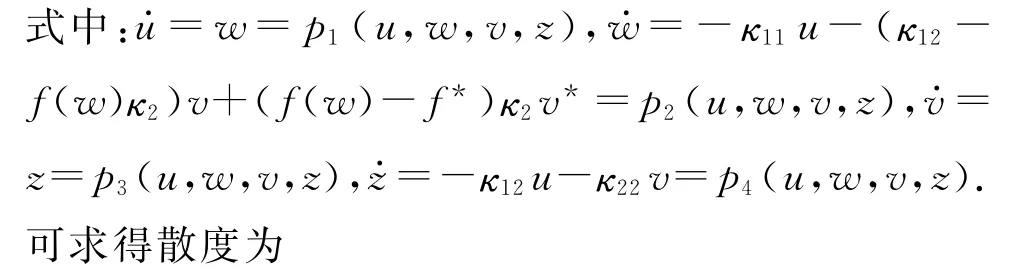

假设带与质点之间始终不脱离,则量纲一化的法向力为nv=-κ2(v+v*)≥0.
根据Bendixson DuΔlac判据[36],Ouw平面内极限环产生的必要条件是 ·P改变符号.因此,只有当df/dw改变符号时才会出现极限环.
3.1 Ⅲ区的黏滑运动特点分析
取摩擦系数参数组合Ⅰ和系统参数组合Ⅰ,系统处于图5中的Ⅲ区,由于,从图2所示的摩擦系数 速度特性中摩擦系数曲线Ⅰ可看出,当|Vrel|非常小时,,因此,质点x方向速度与带速相差较小,此时系统处于黏着阶段;而当|Vrel|比较大时,,因此,质点x方向速度与带速相差较大,此时系统处于滑动阶段.这说明,当极限环出现时,摩擦系数必定在正斜率区与负斜率区之间反复变化,也就是说极限环的出现必然伴随有黏滑现象.下面在不同的带速下进行计算和验证分析.
3.1.1 v0=1.0m·s-1
由于摩擦系数 速度负斜率时线性化系统始终不稳定,导致质点x方向速度达到带速,因此产生了黏滑现象,且产生间断性的多次黏滑现象,并最终进入稳定的极限环(图7a);同时,由于黏滑运动的发生,f变化剧烈,并有可能产生小于零的情况(图7b),即摩擦力会反向,这也与文献[27]的试验现象相符.由图7c可知,质点与带之间没有产生分离.

图7 v0=1.0m·s-1时Ⅲ区的动态响应Fig.7 The dynamical responses in areaⅢwhen v0=1.0m·s-1
改变Δμ=μs-μk进行仿真,对比极限环的变化,如图8所示.分析可知,Δμ越小,极限环越小,黏着段对应的位移区间越小.3.1.2 v0=3.5 m·s-1

图8 Δμ变化引起的极限环的变化Fig.8 Limit cycle varying withΔμ
带速增大,特征值正实部减小,线性化系统越趋向于稳定,而且带速越大,质点速度越难以达到带速(图9a),而且,由于只产生滑动运动时,摩擦系数也比较稳定,无突变发生(图9b).
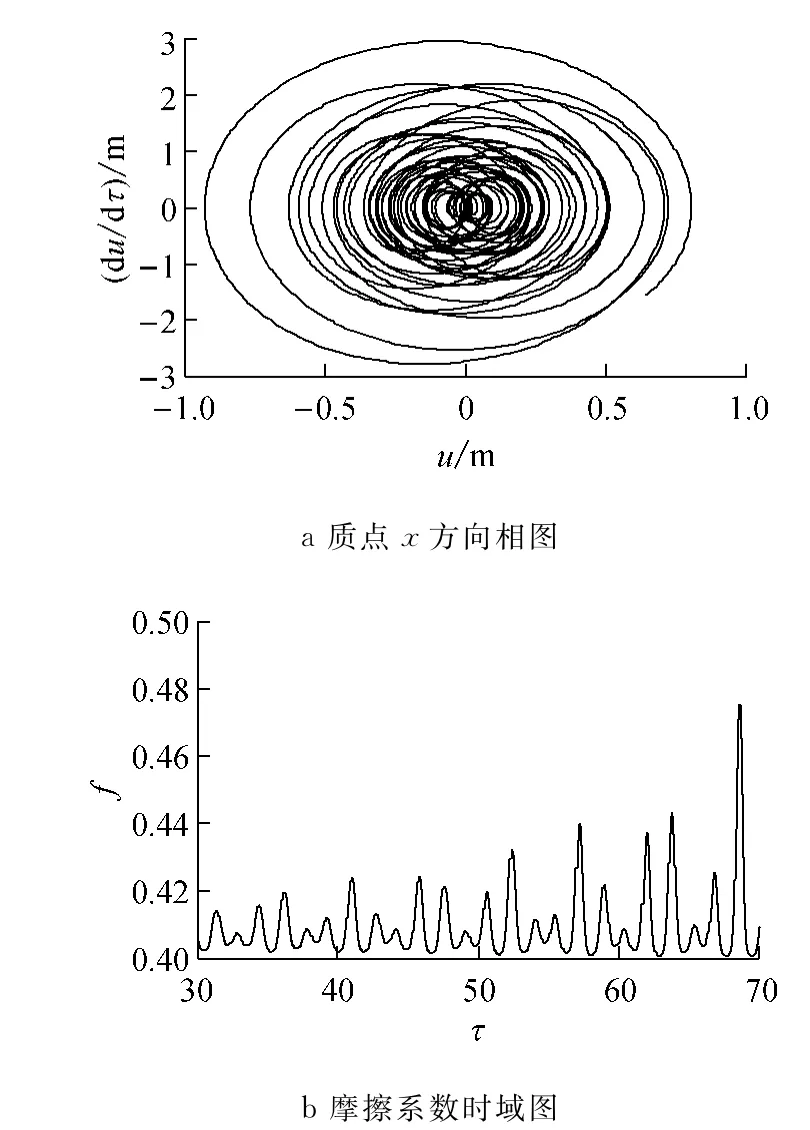
图9 v0=3.5m·s-1时Ⅲ区的动态响应Fig.9 The dynamical respobses in areⅢwhenv0=3.5m·s-1
3.2 Ⅰ区的黏滑运动特点分析
由式(12)可知,β为正时,Δ·P符号不会改变,因此不能产生极限环.
取摩擦系数参数组合Ⅱ和系统参数组合Ⅰ,系统处于图5中的正斜率模态耦合稳定区,在低带速v0=1.0m·s-1下对非线性系统(6)进行仿真计算,相图结果和摩擦系数变化如图10.显然,由于线性化系统特征值具有负实部,系统很快趋于稳定的滑动状态,很难产生黏滑运动,摩擦系数也很稳定.

图10 Ⅰ区的动态响应Fig.10 The dynamical responses in areaⅠ
3.3 Ⅱ区与Ⅳ区的黏滑运动特点分析
此时系统存在模态耦合不稳定,系统不稳定性加剧,质点速度更容易达到带速从而产生黏滑现象.现取μs=0.8,μk=0.95,d=50,h=1,以及系统参数组合I,选取v0=2.0m·s-1进行计算.由图11a可知,当系统在τ=8以后趋向于产生黏滑运动,但由图11b可知,τ=7以后质点与带之间就产生了脱离.也就是说,此时黏滑运动的发生一般伴随有质点与带的间断性分离,这也与文献[28]的现象吻合.由于nv出现了小于零的情况,违反了模型的假设,所以在此不作深入分析.
4 摩擦系数速度斜率产生的Hopf分岔现象
系统只有在β为正时才有可能产生Hopf分岔现象.若Hopf分岔点存在,则可求得Hopf分岔点如下:
当κ12>0时,由

确定.
当κ12<0时,由

确定.
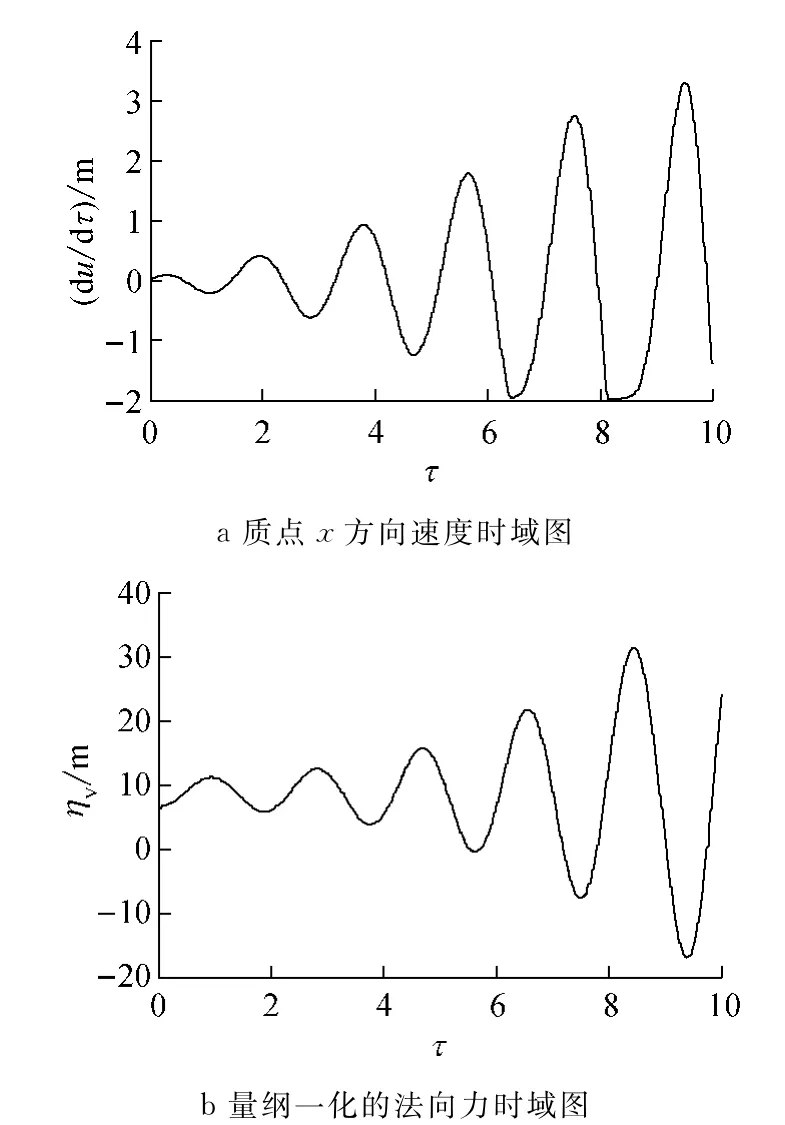
图11 Ⅱ区的动态响应Fig.11 The dynamical responses in areaⅡ
取摩擦系数参数组合Ⅱ以及系统参数组合Ⅰ(仅改变系统参数κ2),v0=3.0m·s-1进行说明.

求出矩阵A(κ2)的特征值λ,计算得到实部和频率随κ2变化的曲线,如图12所示.由图12a可知,当κ2=κ0≈9.488时,只有1对特征值的实部为零,而其余特征值的实部都小于零,且.显然,P(X,κ2)在R4× R包含(0,κ0)的一个邻域内解析,P(0,κ2)=0.因此,κ2=κ0是系统的Hopf分岔点.
运用中心流形定理[37],先将式(11)简化为AX+K(X)的形式,作线性变换Y=T-1X(T-1AT为

图12 实部和频率随κ2变化的曲线Fig.12 The locus of real part and frequency with respect toκ2

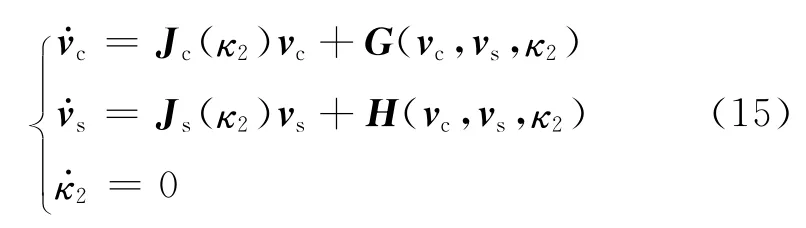
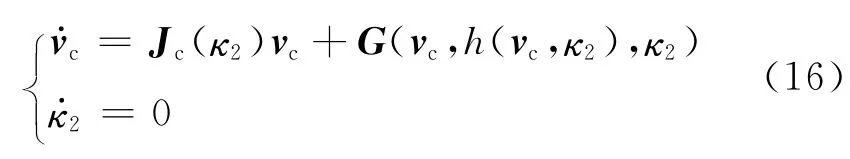
从而可确定系统在κ2=κ0附近系统的轨线情况.通过仿真可知,κ充分小)时,原点为稳定焦点,并在原点邻域内有不稳定的闭轨.图13所示为κ2=κ0-δ(δ=0.05)时的x方向相图中出现的极限环图像;而当κ2>κ0时,原点为不稳定的焦点.
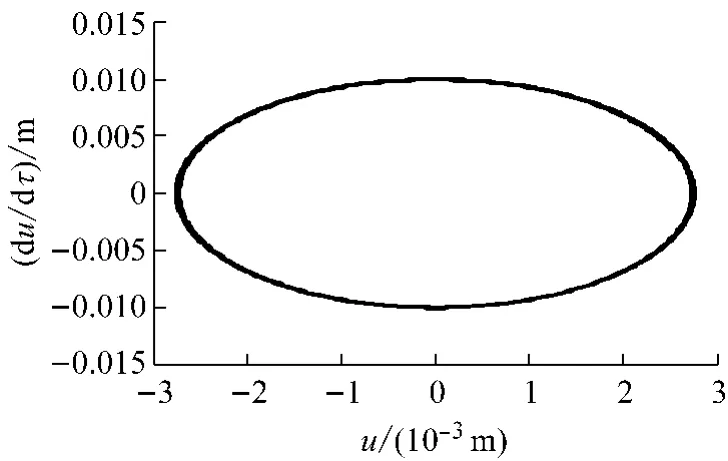
图13 κ2=κ0-δ时质点x方向相图中的极限环Fig.13 Limit cycle of the phase diagram of the mass in x direction whenκ2=κ0-δ
同样地,若改变系统参数κ1,α1,α2等,也可能产生类似Hopf分岔现象,可由式(13)和式(14)确定.
5 结语
针对一类由集总参数柔体 刚体摩擦副构成的摩擦振动系统,建立单质量二自由度非线性摩擦振动动力学模型,采用数学公式推导和数值计算的手段得到以下结论:
(1)由摩擦系数 速度负斜率产生的阻尼矩阵加剧了系统的不稳定;摩擦系数 速度正斜率也能产生模态耦合,而且有时比摩擦系数 速度无斜率时更容易产生模态耦合;摩擦系数 速度斜率的正负与大小并没有改变模态耦合的范围,而且对频率的影响不大.
(2)可根据摩擦系数及其斜率把系统分为4个区域,分别为正斜率无模态耦合稳定区、正斜率模态耦合不稳定区、负斜率无模态耦合不稳定区、负斜率模态耦合不稳定区.
(3)当系统处于负斜率无模态耦合不稳定区时,能否产生黏滑现象一定程度上取决于带速.带速较小时,能产生间断性的多次黏滑运动现象,且最终进入了稳定的极限环运动;但带速较大时,较难产生黏滑现象.当系统处于正斜率无模态耦合稳定区时,由于系统很快稳定下来,所以即使带速很小也难以产生黏滑运动现象.当系统处于正斜率模态耦合不稳定区与负斜率模态耦合不稳定区时,系统产生黏滑运动时会伴随有质点与带的脱离.
(4)仅在摩擦系数 速度正斜率时,当系统参数有微小改变时,在某些特定值附近可能产生Hopf分岔现象.
[1] Akay A.Acoustics of friction[J].Journal of Acoustical Society of America,2002,111(4):1525.
[2] Kinkaid N M,O’Reilly O M,Papadopoulos P.Review of automotive disc brake squeal[J].Journal of Sound and Vibration,2003,267(1):105.
[3] 周仲荣,雷源忠,张嗣伟.摩擦学发展前沿[M].北京:科学出版社,2006.ZHOU Zhongrong,LEI Yuanzhong,ZHANG Siwei.Frontier of tribology[M].Beijing:Science Press,2006.
[4] 国家自然科学基金委员会工程与材料科学部.机械工程学科发展战略报告(2011—2020)[M].北京:科学出版社,2010.Engineering and Materials Science Division of NSFC.Strategy report of mechanical engineering discipline development(2011—2020)[M].Beijing:Science Press,2010.
[5] Hoffmann N,Gaul L.Friction induced vibrations of brakes:research fields and activities[C]//SAE Paper.[S.l.]:SAE,2008:2008-01-2579.
[6] Hoffmann N,Fischer M,Allgaier R,et al.A minimal model for studying properties of the mode-coupling type instability in friction induced oscillations[J].Mechanics Research Communications,2002,29(4):197.
[7] North M R.Disc brake squeal,braking of road vehicles,automobile division of the institution of mechanical engineers[M].London:Mechanical Engineering Publications Limited,1976.
[8] Nishiwaki M.Review of study on brake squeal[J].Japan Society Automobile Engineering Review,1990,11(4):48.
[9] Crolla D A,Lang A M,Brake noise and vibration—the state of the art[J].Tribology Series,1991,18:165.
[10] Ibrahim R A.Friction-induced vibration,chatter,squeal,and chaos—PartⅠ:Mechanics of contact and friction[J].Applied Mechanics Review,1994,47(7):209.
[11] Ibrhim R A.Friction-induced vibration,chatter,squeal,and chaos—PartⅡ:Dynamics and modeling[J].Applied Mechanics Review,1994,47(7):227.
[12] Yang S,Gibson R F.Brake vibration and noise:Reviews,comments and proposals[J].International Journal of Materials and Product Technology,1997,12(4/6):496.
[13] Papinniemi A,Lai J C S,Zhao J,et al.Brake squeal:A literature review[J].Applied Acoustics,2002,63:391.
[14] Ioannidis P,Brooksand P C,Barton D C,et al.Brake system noise and vibration—A review[C]//Proceedings of Braking 2002.From the driver to the road.Leeds:[s.n.],2002:53-73.
[15] Chen F,Quaglia R L,Tan C A,On automotive disc brake squeal partⅠ:Mechanisms and causes[C]//SAE Paper.[S.l.]:SAE,2003:2003-01-0683.
[16] Omar Dessouki,George Drake,Brent Lowe,et al.Disc brake squeal:diagnosis and prevention[C]//SAE Paper.[S.l.]:SAE,2003:2003-01-1618.
[17] OUYANG Huajiang,Nack Wayne,YUAN Yongbin,et al.On automotive disc brake squeal part II:Simulation and analysis[C]//SAE Paper.[S.l.]:SAE,2003:2003-01-0684.
[18] Chen F,Abdelhamid M K,Blaschke P,et al.On automotive disc brake squeal part III:test and evaluation[C]//SAE Paper[S.l.]:SAE,2003:2003-01-1622.
[19] Chen F,Tong H,Chen S E,et al.On automotive disc brake squeal part IV:reduction and prevention[C]//SAE Paper.[S.l.]:SAE,2003:2003-01-3345.
[20] OUYANG Huajiang,Wayne Nack,YUAN Yongbin,et al. Numerical analysis of automotive disc brake squeal:A review[J].International Journal of Vehicle Noise and Vibration,2005,1(3-4):207.
[21] Sergienko V P,Bukharov S N,Kupreev A V.Noise and vibration in brake systems of vehicles.Part 1:Experimental procedures[J].Journal of Friction and Wear,2008,29(3):234.
[22] Sergienko V P,Bukharov S N.Vibration and noise in brake systems of vehicles.Part 2:Theoretical investigation techniques[J].Journal of Friction and Wear,2009,30(3):216.
[23] Cantoni C,Cesarini R,Mastinu G,et al.Brake comfort—A review[J].Vehicle System Dynamics,2009,47(8):901.
[24] 张立军,刁坤,孟德建,等.摩擦引起的振动和噪声的研究现状与展望[J].同济大学学报:自然科学版,2013,41(5):765.ZHANG Lijun,DIAO Kun,MENG Dejian,et al.Literature survey and research prospect of friction induced vibration and noise[J],Journal of Tongji University:Natural Science,2013,41(5):765.
[25] Hoffmann N,Gaul L.Effects of damping on mode-coupling instability in friction induced oscillations[J].Journal of Applied Mathematics and Mechanics,2003,83(8):524.
[26] Sinou J J,Jézéquel L.Mode coupling instability in frictioninduced vibrations and its dependency on system parameters including damping[J].European Journal of Mechanics-A/Solids,2007,26(1):106.
[27] Chen G X,Zhou Z R.Correlation of a negative friction-velocity slope with squeal generation under reciprocating sliding conditions[J].Wear,2003,255(1):376.
[28] Meziane A,D’Errico S,Baillet L,et al.Instabilities generated by friction in a pad-disc system during the braking process[J].Tribology International,2007,40(7):1127.
[29] Kang J,Krousgrill C M,Sadeghi F.Oscillation pattern of stick-slip vibrations[J].International Journal of Non-Linear Mechanics,2009,44(7):820.
[30] Ibrahim R A,Friction induced vibration,chatter,squeal,and chaos,Part2:Dynamics and modeling[J].Applied Mechanics Review,1994,47:227.
[31] Crolla D A,Lang A M.Brakes noise and vibrations—The state of the art[C]//The Proceedings of the Leeds—Lyon Symposium on Tribology.[S.l.]:The University of Leeds,1990:165-174.
[32] Bhushan B.Stick-slip induced noise generation in waterlubricated compliant rubber bearings[J].ASME Journal of Lubrication Technology,1980(102):201.
[33] Bergman F,Mikael E,Eriksson M,et al.Influence of disc topography on generation of brake squeal[J].Wear,1999(225-229):621.
[34] Eriksson M,Bergman F,Jaeobson S.Surface charaeteristic of brake pads after running under silent and squealing conditions[J].Wear,1999(232):163.
[35] D’Souza A F.Design of control systems[J].Zeee Control System Magazine,1982,32(3):364.
[36] Thompson J M T,Stewart H B.Nonlinear dynamics and chaos[M].Chichester:John Wiley &Sons,2002.
[37] Carr J.Application of center manifold[M].New York:Springer,1981.
Relationship among Mode Coupling,Frictionvelocity Slope and Stick-slip Motion
ZHANG Lijun,WU Jun,MENG Dejian
(School of Automotive Studies,Tongji University,Shanghai 201804,China)
Till now,four main frictional squeal mechanisms are highlighted including negative friction velocity slope theory,mode coupling theory,sprag slip motion theory and stick slip motion theory.However,none of them can explain various frictional squeal phenomena fully.So it is very important to make clear the relationship among various mechanisms in order to unify the realization of friction induced vibration and noise.A nonlinear friction induced vibration lamped-parameter model with two degree of freedoms is established,to simulate the friction induced vibration behaviour between a flexible body and a rigid body frictional pairs with single point contact based on friction coefficient and friction velocity slope.By deduction and calculation,effect of friction coefficient and friction velocity slope on mode coupling instability is studied,according to which instability characteristics are summarized in four areas.For each area,stick slip motion,limit cycle and their dependence on working conditions are investigated.At the same time,it is pointed out that the change of system parameters result in the occurrence of Hopf bifurcation under the condition of positive friction velocity slope.
friction induced squeal;friction velocity slope;mode coupling;stick slip motion;Hopf bifurcation
U463
A
0253-374X(2015)12-1850-10
10.11908/j.issn.0253-374x.2015.12.013
2014 11 05
国家自然科学基金(51175380)
张立军(1972—),男,教授,博士生导师,工学博士,主要研究方向为汽车振动与噪声的分析与控制.E-mail:tjedu_zhanglijun@tongji.edu.cn
