基于独立覆盖的高阶流形方法

蔡永昌，刘高扬

（1.同济大学土木工程学院，上海200092；2.同济大学土木工程防灾国家重点实验室，上海200092）

式中：t为平面单元的厚度.可直接得到L12的刚度矩阵为

对于独立覆盖e1，e2，有了位移插值函数式（2）、式（3）后，利用最小势能原理容易导出其刚度矩阵，这里就不具体推导了.Cai等［20］也采用了类似技术利用夹层单元来实现可变形块体间的连接，并将其应用于裂纹分析，本文则是基于流形覆盖理论和间隙位移假定重点讨论基于完全独立覆盖流形方法的高阶特性、线性相关性及其独立覆盖的弹簧连接方式.

图6a所示的独立覆盖间的连接单元可以等效为图6b所示的具有真实物理意义的连接弹簧，利用高斯积分，式（12）可改写为

基于独立覆盖的高阶流形方法

蔡永昌1，2，刘高扬1

（1.同济大学土木工程学院，上海200092；2.同济大学土木工程防灾国家重点实验室，上海200092）

提出了一种基于独立覆盖的高阶流形方法（ICMM）.该方法基于完全独立的物理覆盖，在物理覆盖上可以定义一至高阶的覆盖位移函数，在独立的物理覆盖间采用具有真实物理意义的弹簧（区别于DDA（Discontinuous Deformation Analysis）和DEM（Discrete Element Method）方法中为迭代需要而设置的虚拟弹簧），避免了一般流形方法需要复杂的覆盖生成等前处理算法的困难，消除了高阶流形方法特有的线性相关性带来的总体刚度矩阵奇异性的问题，可以方便地应用于连续体分析、从连续到非连续破坏以及完全非连续问题的统一分析.算例分析初步验证了本文方法的正确性和有效性.

流形方法；高阶；独立覆盖；线性相关性

基于有限覆盖系统的流形方法NMM（Numerical Manifold Method）可以方便统一地处理连续和非连续问题的分析，它采用独立且分开的数学网格和物理网格，将包含某一结点的所有数学单元的集合定义为该结点的数学覆盖（或影响域），材料边界、裂纹等物理线进一步剖分数学覆盖为具有不同变形自由度的物理覆盖，从而可以在保持数学网格不变的前提下，方便地实现节理、裂隙等扩展破坏过程的动态模拟，且可以在保持结点数目不变的条件下，在物理覆盖上直接采用高阶的或者解析形式的覆盖函数，方便实现应力高梯度区域的p型自适应分析.

由于流形方法在连续 非连续统一分析方面的理论优势，近年来在岩体力学及相关分析领域内得到了极大的重视和发展，例如Ma等［1］、李树忱等［2］对流形方法的理论进展及其应用进行了综述，Cai等［3］结合物理线的符号函数表达方式发展了简单高效的流形方法覆盖系统生成算法，陈刚等［4］探讨了基于有向遍历理论的流形元覆盖系统，朱爱军等［5］、武杰等［6］、蔡永昌等［7］也从不同角度出发对流形方法的覆盖系统进行了研究，李海枫等［8］进一步研究了三维情形下的流形单元生成，姜清辉等［9］对三维数值流形方法的点 面接触模型进行了研究，郭朝旭等［10］、Zheng等［11］对高阶数值流形方法中存在的线性相关问题及其解决方法进行了探讨和研究.在XFEM（Extended Finite Element Method），GFEM（Generalized Finite Element Method），PU（Partition of Unity）等方法中也普遍存在类似的线性相关性问题［12-17］.

从这些典型的代表性成果可以看出，流形方法的流形覆盖系统生成算法以及采用高阶覆盖位移函数时的线性相关性带来的总刚度矩阵奇异性等问题是最近十多年来流形方法最迫切要解决的问题和研究焦点所在.但限于现有的数学和力学理论，直接解决这些困难使其可以方便地应用于复杂多节理、多裂纹的实际工程问题的分析求解在短期内仍难预期有较明显的发展.苏海东等［18-19］提出的部分覆盖流形方法对上述困难的解决提供了一种新的思路与方向，采用“部分重叠覆盖”替代通常的“完全重叠覆盖”，避免了流形方法在高阶时的线性相关性问题，可以方便地加密覆盖，方便地在局部应用解析解等，为流形方法的发展提供了新的思路和方向.但是部分覆盖流形方法在独立覆盖间采用条带连接，给前处理、后处理及算法实现等带来了一些麻烦，实际应用于复杂工程分析时仍有一些不便之处.

为了解决部分覆盖流形方法存在的问题，本文提出了一种基于完全独立覆盖的高阶流形方法（ICMM），在该方法中，高阶位移函数定义在完全独立的物理覆盖上，在独立覆盖之间假设几何厚度可以忽略的连接弹簧（区别于DDA（Discontinuous Deformation Analysis），DEM（Discrete Element Method）纯粹为迭代需要而设置的虚拟弹簧）.这种方法解决了高阶流形方法的线性相关性问题和需要复杂算法生成物理覆盖系统的困难，具有部分覆盖流形方法的其他优点，但避免了部分覆盖流形方法需要生成条带连接带来的相关麻烦.

1 基于完全独立覆盖的流形方法

如图1所示的具有2条裂纹的物体Ω，采用流形方法进行分析时，可首先定义如图2所示的三角形（或任意形状）有限元网格.以图2中的3 5 7数学单元为例，在NMM（Numerical Manifold Method）中，结点的数学覆盖（或影响域）定义为围绕该结点的所有数学单元集合，如图3所示的数学覆盖3，5，7（数学覆盖3，5，7的公共区域为数学单元3 5 7，称这样的数学覆盖定义方法为“完全重叠的覆盖”）.裂纹、材料边界等的物理线进一步剖分数学覆盖为独立变形的物理覆盖区域，如图4中的数学覆盖3被裂纹线剖分成了物理覆盖31，32，33.

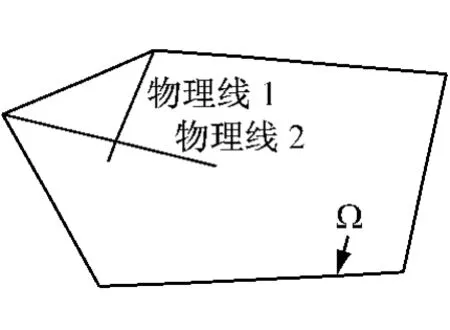
图1 含2条裂纹的分析物体Fig.1 An arbitrary domain with 2cracks

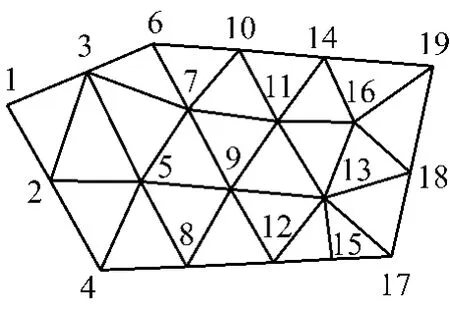
图2 有限元网格（数学网格）Fig.2 Finite element mesh（Mathematical mesh）

图3 数学覆盖定义Fig.3 Definition of mathematical covers

有了物理覆盖的定义后，NMM就可以在这些物理覆盖上采用各种形式的多项式来定义覆盖位移函数，例如在裂尖所在的物理覆盖32上采用来自解析解的局部覆盖位移函数如下：

式中：u-

32（x-，y-）为局部覆盖32的位移函数；x-，y-为全局坐标；a32＝［d31，d32，d33，…］T，d31，d32，d33，…为物理覆盖32的覆盖自由度；F32＝，其中r，θ为裂尖局部极坐标值.

利用单位分解法和这些独立定义的物理覆盖函数即可定义出分析区域上的任意点（x-，y-）处的总体位移函数.可以发现，NMM可以在保持数学网格不变的条件下，方便实现连续和不连续统一分析，但是从NMM的实施过程可以看出物理覆盖的剖分需要复杂、耗时的几何算法和点 区域判断算法，对其进行三维分析的难度更高，同时高阶位移函数的线性相关性也是一个难以避免的问题.

为了解决流形方法存在的这些困难，本文提出了如下的思路与方法.仍以图2中的单元3 5 7和3 7 6为例，如图5所示.

图4 物理覆盖定义Fig.4 Definition of physical covers

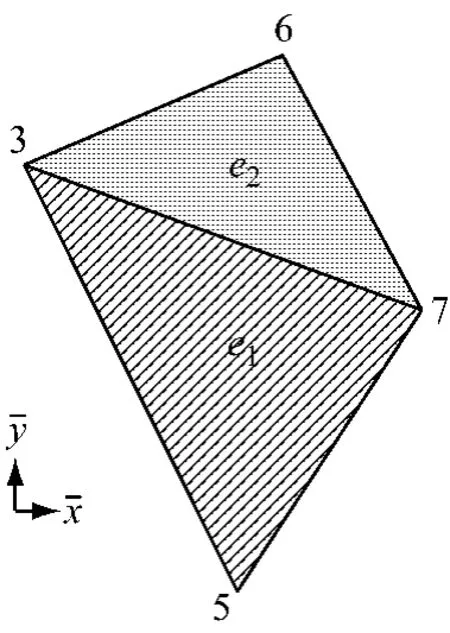
图5 独立覆盖Fig.5 Independent cover

区别于前面的完全重叠的流形覆盖，本文将单元e1（即3 5 7）和单元e2（即3 7 6）定义为完全独立的覆盖，其覆盖函数取为

式中

可根据需要取为一阶至多阶的简单多项式或其他级数形式，其中x-c＝x--x-0，y-c＝y--y-0，x-0，y-0为相应多边形单元的中心点坐标；分别为x-，y-方向的位移函数；a＝［a1a2… a3］为覆盖自由度.

假设覆盖e1和覆盖e2之间存在一宽度为b的间隙L12，如果b值取得很小，例如b＝l／10 000（l为3 7边长）时，间隙L12里任意点p（x，y）在局部坐标下的位移u（x，y），v（x，y）可插值表示为

式中：up1，vp1为图6a中覆盖e1在p1点处局部坐标（x，y）下的位移，可由式（2）坐标转换得到；up2，vp2为图6a中覆盖e2在p2点处局部坐标（x，y）下的位移，可由式（3）进行坐标转换得到，图6b中g1，g2，gi为高斯点位置.

图6 独立覆盖之间的弹簧连接Fig.6 Springs between adjacent independent covers

在b很小的情况下，间隙L12里任一点p的应变可近似由式（5）、式（6）求得.

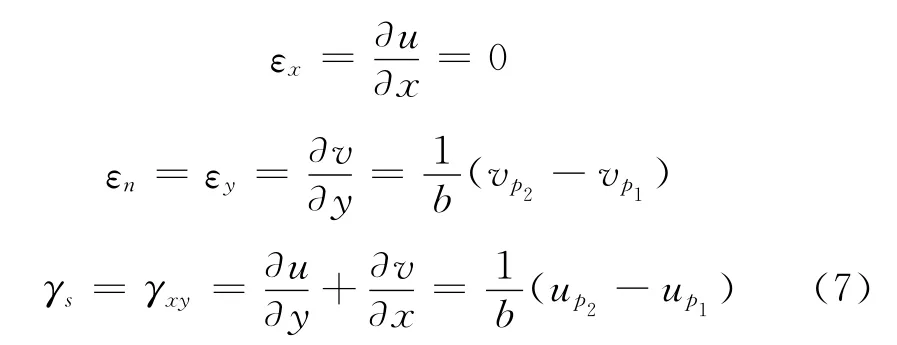
式中：εx，εy为x，y方向正应变；εn，γs分别为间隙L12的法向应变和切向应变；γxy为切应变.

利用式（2）、式（3）、式（7）可进一步表示为

式中：ε为应变向量；下标s，n分别表示切线方向和法线方向；B为应变矩阵，为自由度向量，为覆盖e1，e2交界边3 7的局部坐标转换矩阵.

对于弹性分析，根据广义胡克定律，p点处的应力可表示为

式中：τs，σn分别为间隙L12的切向应力和法向应力；S为应力矩阵，S＝D·B，D为弹性矩阵，对于平面应力问题，有

式中：G＝E／［2（1＋ν）］，E为弹性模量，ν为泊松比.于是，间隙L12的势能可表示为

式中：t为平面单元的厚度.可直接得到L12的刚度矩阵为

对于独立覆盖e1，e2，有了位移插值函数式（2）、式（3）后，利用最小势能原理容易导出其刚度矩阵，这里就不具体推导了.Cai等［20］也采用了类似技术利用夹层单元来实现可变形块体间的连接，并将其应用于裂纹分析，本文则是基于流形覆盖理论和间隙位移假定重点讨论基于完全独立覆盖流形方法的高阶特性、线性相关性及其独立覆盖的弹簧连接方式.

图6a所示的独立覆盖间的连接单元可以等效为图6b所示的具有真实物理意义的连接弹簧，利用高斯积分，式（12）可改写为

式中：n为总的高斯点数；（Ks）gi，（Kn）gi分别为第i个高斯点处的等效弹簧切向和法向刚度，（Ks）gi＝高斯点gi的实际坐标值也可由高斯积分的积分点坐标求出；Hi为第i个高斯点的权函数；Δugi，Δvgi分别为第i个高斯点处弹簧的相对切向和法向变形，Δugi＝（ugi）e2-（ugi）e1，Δvgi＝（vgi）e2-（vgi）e1，（ugi）e1，（vgi）e1分别为高斯点gi在覆盖e1处的x，y方向位移值，可由式（2）坐标转换求得，同理可以求得（ugi）e2，（vgi）e2.

式（14）中的（Ks）gi，（Kn）gi即为推导得出的如图6b所示的真实弹簧的等效切向和法向刚度.

上述推导过程将独立覆盖间的连接弹簧等效为真实的弹簧，极大区别于DEM，DDA等方法中为迭代需要而设置的不具物理意义的虚拟弹簧，可以方便模拟分析连续体，当弹簧受拉、受剪破坏后，直接移除弹簧，即可轻易实现非连续分析.

当断层、裂纹穿越独立覆盖内部时，传统流形方法需要采用比较复杂的覆盖生成算法来分别生成物理线切割后的物理覆盖、流形单元，而在本文方法中，不再需要复杂、耗时的点 区域判断等算法来分别处理物理覆盖和流形单元，例如图7的独立覆盖3 5 7被2条裂纹线穿越（裂纹线在独立覆盖内部未贯穿时也按同样方法处理），仅需将覆盖3 5 7简单再分为C1，C2，C3三个独立覆盖（其中分割后的独立覆盖C1和C2为三角形、独立覆盖C3为任意四边形，注意当独立覆盖为大于三边的多边形时需在该覆盖上采用二阶以上的覆盖函数），独立覆盖间采用式（14）的弹簧进行连接，所有的插值和积分运算在分割后的独立覆盖上即可轻易完成.同时，本文方法也可灵活地在应力高梯度区域采用高阶覆盖函数提高精度，而不会有线性相关性的问题.

图7 裂纹切割的独立覆盖Fig.7 Independent cover cut by cracks

需要指出的是，图6中的覆盖e1，e2交界处分开一段距离只是为了显示和表达的需要，在实际实施本文方法时，如果独立覆盖e1，e2没有断裂分开或发生非连续变形，则它们之间的交界处在几何上共用3，7结点.

2 施加位移边界条件

设图1的独立覆盖1-2-3的边界1-2上作用有图8a所示的沿边界1-2的法向给定位移v10，v20.

按照独立覆盖之间交界处的同样思路，假定在覆盖1-2-3的边界1-2处存在一宽度为b的微小间隙L（图8b），则间隙L里任意一点p（x，y）处的位移可近似插值为

式中

式中：l为边1-2的长度；λ为边界1-2的坐标转换矩阵.

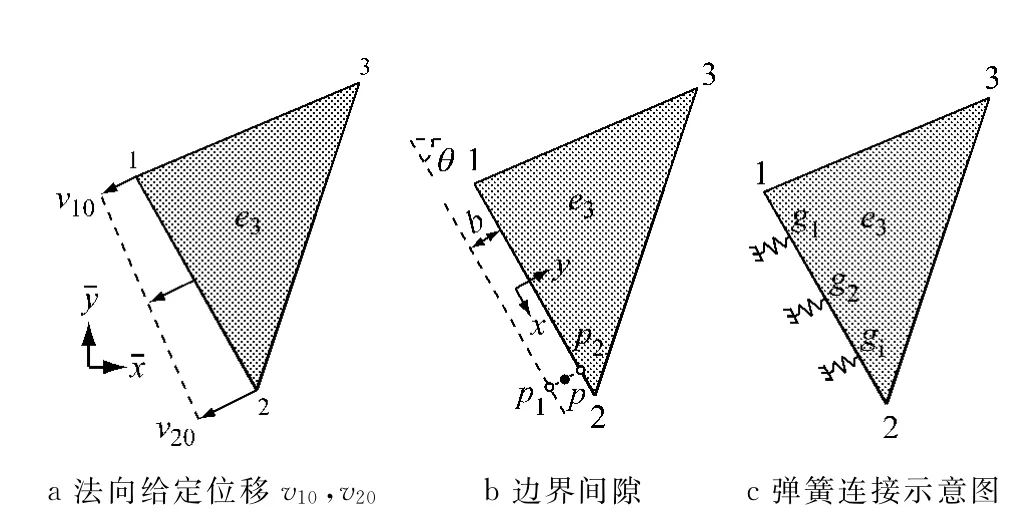
图8 位移边界条件Fig.8 Displacement boundary conditions

有了式（15）后，按照式（14）同样的步骤可以推导得出图8c所示的边界处的等效弹簧刚度.如果在边界上作用有切向的给定位移或者仅作用有给定点的位移，其推导过程与方法类似.

3 算例

3.1 线性相关性检验

如前所述，采用高阶覆盖位移函数的流形方法（或PU，XFEM等）面临的一个主要困难是线性相关带来的总刚矩阵奇异问题.采用图9所示的算例来检验ICMM的线性相关性，表1和表2给出了分别采用线性覆盖函数和二次覆盖函数时施加限制刚体位移的最少边界条件后的总自由度数和总体刚度矩阵的零特征值数，可以发现，对于各种情形，总体刚度矩阵均未出现零特征值，表明ICMM完全消除了原有高阶流形或单位分解法固有的线性相关问题.

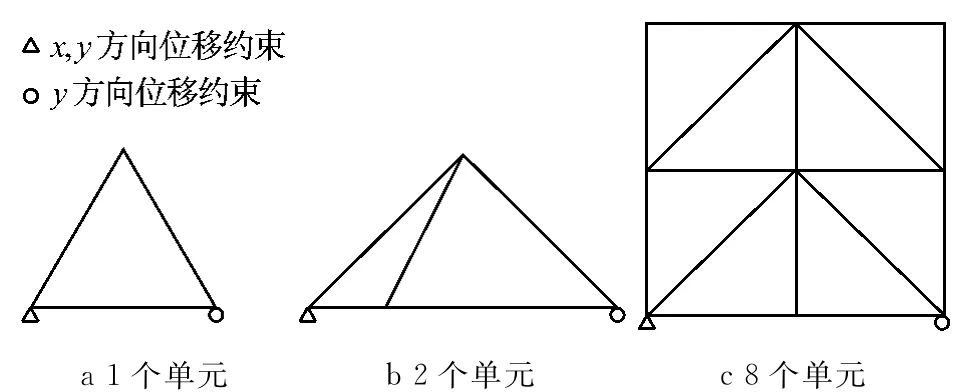
图9 线性相关性算例Fig.9 Test examples for checking of linear dependence

表1 线性覆盖函数时的总刚矩阵Tab.1 Global stiffness matrix with linear functions

表2 二次覆盖函数时的总刚矩阵Tab.2 Global stiffness matrix with quadratic functions

3.2 悬臂梁

如图10所示的悬臂梁，长L＝8m，宽W＝1m，弹性模量E＝1×103Pa，泊松比ν＝0.25，在梁的末端受均布荷载F＝1N作用，按平面应力问题分析，悬臂梁末端A点竖向位移的解析解［21-22］为2.069m.

图10 悬臂梁Fig.10 Cantilever beam

分别采用50，138，487三种离散结点的网格以及线性和二次覆盖函数进行了分析.从表3可以看出，当采用线性覆盖函数时，ICMM的计算结果与对应的三角形有限单元法结果一致，随着结点数的增加，计算结果逐渐趋于解析解答；当采用二次覆盖函数时，对于各种不同数目的离散结点，ICMM均能得到与解析解吻合较好的计算结果，这也说明了ICMM可以在保持结点数目不变的情况下仅提升覆盖函数的阶次即可轻易实现p型自适应分析.当然ICMM也能像其他数值方法一样依靠加密网格来实现h型自适应分析.

表3 A点的竖向位移Tab.3 Vertical displacement of point A

3.3 Cook梁

如图11所示的Cook梁，在梁的右端作用有F＝1／16的均布剪力，按照平面应力问题求解，A点竖向位移的参考解［23］为23.96.设梁的弹性模量E＝1.0，泊松比ν＝1／3.分别采用80，206两种离散结点的网格以及线性和二次覆盖函数进行了分析.表4给出的各种情况下Cook梁右端点A处的竖向位移VA计算结果，同样表明了ICMM良好的p型和h型自适应分析能力.

图11 Cook梁模型Fig.11 Cook’s skew beam

表4 Cook梁A点的竖直位移Tab.4 Vertical displacement of point Afor Cook beam

4 结语

不同于常规数值流形方法和部分覆盖数值流形方法，本文方法采用完全独立的物理覆盖，在独立覆盖上定义一至高阶的覆盖函数，在物理独立覆盖间采用具有物理意义的真实弹簧进行连接，从而避免了常规流形方法需要复杂覆盖算法和部分覆盖流形方法需要构造条带连接的困难，大大降低了流形方法的前处理难度，同时也完全消除了高阶流形方法特有的线性相关性问题，可以方便进行连续体分析以及从连续到非连续破坏的统一分析.

以三角形独立覆盖为例推导了ICMM的实现过程，并用弹性连续分析算例对其正确性和可靠性进行了验证.该方法可以采用任意形状的多边形覆盖或者无网格覆盖，且可以很容易地推广应用到岩土结构渐进性破坏和三维静、动力分析等领域，这也将是下一步的工作和研究方向.

［1］ Ma G W，An X M，He L.The numerical manifold method：A review［J］.International Journal of Computational Methods，2010，7：1.

［2］ 李树忱，程玉民.数值流形方法及其在岩石力学中的应用［J］.力学进展，2004，34（4）：446.LI Shuchen，CHENG Yumin.Numerical manifold method and its applications in rock mechanics［J］.Advances in Mechanics，2004，34（4）：446.

［3］ Cai Y C，Wu J，Atluri S N.A new implementation of the numerical manifold method（NMM）for the modeling of noncollinear and intersecting cracks［J］.CMES：Computer Modeling in Engineering ＆Sciences，2013，92（1）：63.

［4］ 陈刚，刘佑荣.流形元覆盖系统的有向图遍历生成算法研究［J］.岩石力学与工程学报，2003，22（5）：711.CHEN Gang，LIU Yourong.Generation of cover system for numerical manifold in travel theory of the oriented graph［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（5）：711.

［5］ 朱爱军，邓安福，颜昌武，等.岩体材料物理网格对流形元覆盖系统形成的影响［J］.岩土力学，2004，25（2）：1933.ZHU Aijun，DENG Anfu，YAN Changwu，et al.Effects of physical grid in rock mass for generation of cover system for numerical manifold method［J］.Rock and Soil Mechanics，2004，25（2）：1933.

［6］ 武杰，蔡永昌.基于四边形网格的流形方法覆盖系统生成算法［J］.同济大学学报：自然科学版，2013，41（5）：641.WU Jie，CAI Yongchang.Generation algorithm of the cover system in manifold method with quadrangular meshes［J］.Journal of Tongji University：Natural Science，2013，41（5）：641.

［7］ 蔡永昌，朱合华，夏才初.流形方法覆盖系统自动生成算法［J］.同济大学学报：自然科学版，2004，32（3）：585.CAI Yongchang，ZHU Hehua，XIA Caichu.Automatically forming of cover system in numerical manifold method［J］.Journal of Tongji University：Natural Science，2004，32（3）：585.

［8］ 李海枫，张国新，石根华，等.流形切割及有限元网格覆盖下的三维流形单元生成［J］.岩石力学与工程学报，2010，29（4）：731.LI Haifeng，ZHANG Guoxin，SHI Genhua，et al.Manifold cut and generation of three-dimensional element under FE mesh cover［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29（4）：731.

［9］ 姜清辉，周创兵，张煜.三维数值流形方法的点 面接触模型［J］.计算力学学报，2006，23（3）：569.JIANG Qinghui，ZHOU Chuangbing，ZHANG Yu.A model of point-to-face contact for three-dimensional numerical manifold method［J］.Chinese Journal of Computational Mechanics，2006，23（3）：569.

［10］ 郭朝旭，郑宏.高阶数值流形方法中的线性相关问题研究［J］.工程力学，2012，29（12）：228.GUO Chaoxu，ZHENG Hong.Study on linear dependence problem in high-order numerical manifold method［J］.Engineering Mechanics，2012，29（12）：228.

［11］ Zheng H，Xu D D.New strategies for some issues of numerical manifold method in simulation of crack propagation［J］.International Journal for Numerical Methods in Engineering，2014，97：986.

［12］ Babuška I，Melenk J M.Partition of unity method［J］.International Journal for Numerical Methods in Engineering，2001，40：727.

［13］ Rajendran S，Zhang B R.A“FE-meshfree“QUAD4 element based on partition of unity［J］.Computer Methods in Applied Mechanics and Engineering，2007，197：128.

［14］ Cai Y C，Zhuang X Y，Augarde C E.A new partition of unity finite element free from the linear dependence problem and possessing the delta property［J］.Computer Methods in Applied Mechanics and Engineering，2010，199（17）：1036.

［15］ An X M，Li L X，Ma G W，et al.Prediction of rank deficiency in partition of unity-based methods with plane triangular or quadrilateral meshes［J］.Computer Methods in Applied Mechanics and Engineering，2011，200：665.

［16］ Tian R，Yagawa G，Terasaka H.Linear dependence problems of partition of unity-based generalized FEMs［J］.Computer Methods in Applied Mechanics and Engineering，2006，195：4768.

［17］ De Luycker E，Benson D J，Belytschko T，et al.X-FEM in isogeometric analysis for linear fracture mechanics［J］.International Journal for Numerical Methods in Engineering， 2011，87：541.

［18］ 苏海东，祁勇峰，龚亚琦，等.任意形状覆盖的数值流形方法初步研究［J］.长江科学院院报，2013，30（12）：91.SU Haidong，QI Yongfeng，GONG Yaqi，et al.Preliminary research of numerical manifold method based on covers of arbitrary shape［J］.Journal of Yangtze River Scientific Research Institute，2013，30（12）：91.

［19］ 苏海东，祁勇峰.部分重叠覆盖流形法的覆盖加密方法［J］.长江科学院院报，2013，30（7）：95.SU Haidong，QI Yongfeng.Cover refinement for numerical manifold method with partially overlapping covers［J］.Journal of Yangtze River Scientific Research Institute，2013，30（7）：95.

［20］ Cai Y C，Zhu H H，Zhuang X Y.A continuous／discontinuous deformation analysis（CDDA）method based on deformable blocks for fracture modeling［J］.Frontiers of Structural and Civil Engineering，2013，7（4）：369.

［21］ Belytschko T，Lu Y Y，Gu L.Element-free Galerkin methods［J］.International Journal for Numerical Methods in Engineering，1994，37：229.

［22］ Augarde C E，Deeks A J.The use of Timoshenko’s exact solution for a cantilever beam in adaptive analysis［J］.Finite Elements in Analysis and Design，2008，44（9-10）：525.

［23］ Cook R D，Malkus D S，Plesha M E.Concepts and Applications of Finite Element Analysis［M］.3rd ed.New York：John Wiley，1989.

High-order Manifold Method with Independent Covers

CAI Yongchang1，2，LIU Gaoyang1
（1.College of Civil Engineering，Tongji University，Shanghai 200092，China；2.State Key Laboratory of Disaster Reduction in Civil Engineering，Tongji University，Shanghai 200092，China）

An independent cover based manifold method（ICMM）is presented.In the ICMM，various high-order cover functions can be naturally employed at the independent covers，and the springs with real physical significance are defined between the adjacent independent covers，which are different from the virtual springs in DDA（Discontinuous Deformation Analysis）and DEM（Discrete Element Method）.The requirement for the complex algorithm for cover generation in conventional NMM（Numerical Manifold Method），and the rank deficiency due to the linear dependence of the global degrees of freedom in high-order NMM are well treated in the present ICMM.The continuous deformation analysis，the discontinuous deformation analysis，and the switch from continuous analysis to discontinuous analysis can be unified in a same framework in the ICMM.Several test examples indicate the correctness and the validity of the proposed method.

manifold method；high-order；independent cover；linear dependence

TU443

A

0253-374X（2015）12-1794-07

10.11908／j.issn.0253-374x.2015.12.005

2014 09 04

国家自然科学基金（11472194）；国家“九七三”重点基础研究发展计划（2011CB013800）；教育部新世纪优秀人才支持计划（NCET-12-0415）

蔡永昌（1972—），男，教授，工学博士，主要研究方向为岩土计算方法.E-mail：yc_cai@163.net