配体外预应力钢束的曲线箱梁桥抗扭设计

沈 殷，宋泰宇，李国平

（同济大学土木工程学院，上海200092）

配体外预应力钢束的曲线箱梁桥抗扭设计

沈 殷，宋泰宇，李国平

（同济大学土木工程学院，上海200092）

为了抵抗曲线箱梁桥的扭转效应、改善结构的受力状态，在不增加预应力钢束数量的前提下，提出一种利用体外预应力钢束形成空间抗扭作用的方法.基于空间解析几何关系推导了体外预应力扭矩计算公式，以此建立了以最小扭矩为目标的体外预应力钢束的抗扭设计流程，并利用非线性规划方法给出钢束最优平面线形参数的数值解法.分析结果表明，与体内预应力钢束相比，通过合理的体外预应力钢束空间布置，能大幅降低扭矩峰值，抗扭效果明显，且不影响抗弯、抗剪能力；扭矩计算数值解与有限元分析结果吻合良好，能方便地用于实际设计.

曲线箱梁；预应力扭矩；空间解析几何；非线性规划

曲线梁桥能很好地克服地形、地物的限制，满足路线整体线形的连续性、流畅性，在国内外城市高架、立交桥梁工程以及高等级公路中得到了广泛应用.由于结构上的特点，即使在横向对称竖向力作用下曲线梁中也同时产生弯矩和扭矩，并且互相影响，即弯扭耦合效应［1］.因此，大部分曲线梁采用抗弯、抗扭能力均较大的箱形截面［2］.在跨径较大时，曲线梁桥一般采用预应力结构，但其预应力钢束（简称“钢束”）的配束设计与一般直线梁桥不同，主要在于如何利用预应力抵抗外扭矩［3］.曲线箱梁桥的抗扭设计的基本目标是调整梁内的扭矩分布、控制扭矩峰值，使梁截面以及支座受力较均匀［1］.当前预应力曲线箱梁基本采用体内预应力钢束（简称“体内钢束”），而体内钢束因受制于箱梁截面，导致预应力的抗扭作用难以充分发挥，额外配置抗扭预应力钢筋将提高建设成本.

为了利用体外预应力扭矩消除结构重力引起的扭矩，并预留适当的预应力扭矩部分抵抗其他外荷载产生的扭矩，本文基于预应力在曲线箱梁中的抗扭原理，利用体外预应力钢束（简称“体外钢束”）位于混凝土箱梁截面外可同时平弯和竖弯的特点，提出在曲线箱梁桥预应力设计中采用体外预应力抵抗扭矩的方法，在不增加钢束数量的前提下，调整抗弯钢束平面线形以提供高效的扭矩抗力；通过空间解析几何关系建立并推导体外预应力扭矩计算公式；进一步以最小化主梁扭矩峰值为目标，建立体外钢束抗扭设计流程，利用非线性规划得到最优化钢束线形；最后，建立可方便用于满足结构永久和可变作用状态受力要求的设计方法.

1 预应力抗扭原理

如图1所示，将预加力合力F沿曲线梁截面竖向、径向和轴向进行分解，可得到竖向、径向和轴向分力为Fz′s，Fh′s和F（R＋h）θ′s，其中：z，h分别为预加力作用点截面质心（CG）的竖向、径向坐标，z′s＝dz／ds，h′s＝dh／ds，θ′s＝dθ／ds，θ为曲线梁圆心角，ds为钢束微段，ds≈（R＋h）dθ，R为曲率半径.将F等效至CG，截面内力见图1，其中：M（F），N（F），V（F），T（F）分别表示预应力作用产生的弯矩、轴力、剪力和扭矩，脚标M，N分别表示曲线梁的径向、竖向［3］.

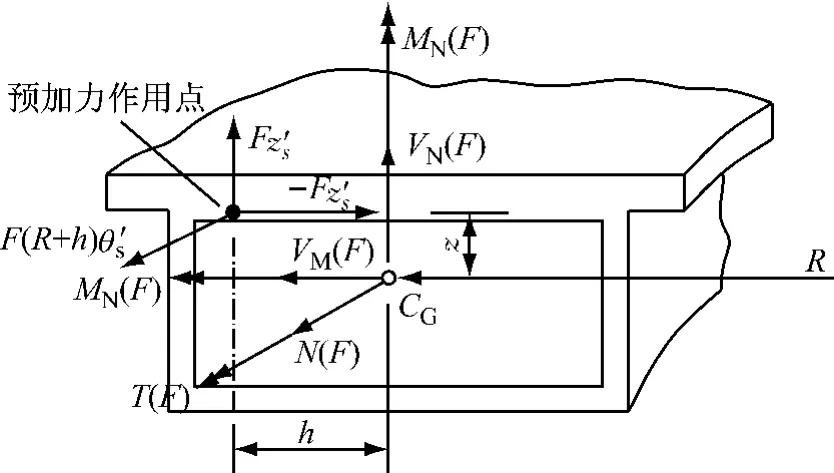
图1 截面上预应力分量和内力表示Fig.1 Component of prestressing and internal force on section

根据力的平衡条件，略去高阶微量，可得

式中：z′，h′分别为z，h对θ的导数.从式（1）可以看出，T（F）取决于其参数F，z，h，z′，h′，而作为钢束立面线形要素的竖向坐标z及其导数z′和预加力F通常根据抗弯、抗剪要求来确定，而径向坐标h及其导数h′在体内预应力设计中因受制于截面而通常为常量.

在曲线梁桥预应力设计中通常考虑预应力提供的扭矩应首先抵消结构重力引起的扭矩，并提供适当的预扭矩部分抵消其他作用在梁内产生的扭矩.传统预应力设计基本采用体内钢束形式［4-11］，目前国内外有几种预应力抗扭布置理论如下：①内外侧腹板采用不同线形的钢束（图2a）［45］；②内外腹板钢束线形对称，但张拉力不同或配置根数不同（图2b）［610］；③在顶底板中布置弯曲方向相反的钢束（图2c）［11］.

方法①通过调整式（1）中参数z′来提供所需的T（F），对预应力的纵向抗弯效应将造成一定影响，且截面提供的可调整范围有限；方法②通过设计内外侧腹板的不同预加力大小来调整式（1）中参数h，是实践中使用较多的方法；方法③通过专门在顶底板中配置抗扭钢束来调整式（1）中参数h′来实现抗扭，有时需要增加额外配筋量，实际工程中容易导致大量钢束的交叉碰撞，增加设计和施工难度.另外体内钢束在曲线箱梁桥的工程应用中还存在腹板崩裂的情况，为此需设置额外的防崩钢筋.

而体外钢束布置在箱内摆脱了混凝土箱梁腹板的束缚，在梁宽方向有足够的布束空间，以满足预加力作用点径向位置的变化要求，即式（1）中h及h′均易作较大幅度调整.所以，对于体外预应力曲线箱梁桥不必专门配置抗扭钢束，可以在一组抗弯钢束的基础上通过将其沿径向位置调整达到同时抵抗弯矩和扭矩的效果.

图2 曲线梁的抗扭钢束布置Fig.2 Layout of torsion-resistant prestressing tendons in curved girder

2 体外预应力扭矩计算公式

根据式（1），T（F）可分为两部分，即

式中：TP（F），TS（F）分别表示钢束平弯、竖弯产生的扭矩，TP（F）＝-Fh′z／（R＋h），TS（F）＝Fz′h／（R＋h）.

以曲梁圆心为原点、对称中心线为y轴，建立水平面内的直角坐标系（图3），对于对称箱梁截面，各截面质心连线与梁轴线水平投影重合，转向点之间、转向点与锚固点之间的体外钢束水平投影方程可表示为

式中：a，b分别为水平投影方程的斜率和纵截距.

图3 体外钢束水平投影Fig.3 Horizontal projection of external tendons

投影方程满足几何关系：x＝（R＋h）cosθ，y＝（R＋h）sinθ，由式（3）可推导得

以曲线梁截面质心连线与对称中心线交点为原点、质心连线竖向投影为x′轴，建立竖直曲面内的直角坐标系（图4），体外钢束竖向投影方程表示为

式中：c，d分别为竖向投影方程的斜率和纵截距.

图4 体外钢束竖向投影Fig.4 Vertical projection of external tendons

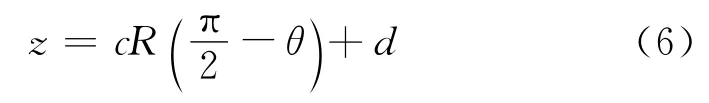
将式（4）、式（6）代入式（2），可得

根据文献［12］的推导，取ds≈Rdθ的假定，式（9）可简化表达为

将式（8）、式（10）代入式（2），有

3 体外预应力抗扭设计方法

3.1 设计思路

基于预应力混凝土桥梁的一般设计方法，结合上述预应力抗扭原理和体外预应力扭矩的计算公式，在不增加钢束数量的前提下，对体外钢束的横向布置进行优化设计，使钢束能提供足够的抗扭力以平衡设计的外荷载扭矩.

体外预应力抗扭设计目标为在需要抵抗的外荷载和预应力共同作用下的主梁扭矩峰值达到最小.以曲线梁控制截面的扭矩峰值T为目标函数，对钢束沿梁长的径向偏距进行最优化设计.当需要抵抗的外荷载扭矩一定时，根据式（10），目标量T为预加力F以及体外钢束水平、竖向投影的斜率a，c和纵截距b，d的函数，其中F和c，d由抗弯、抗剪设计确定，T仅为a，b的函数，在可行域内对该函数进行非线性规划，即可得到目标量取到最小值时的最优参数解［a b］＊，从而得到最优体外钢束平面线形.其中，控制截面为出现扭矩极值的截面，一般为体外钢束转向点和锚固点截面，根据式（4）、式（10）可得

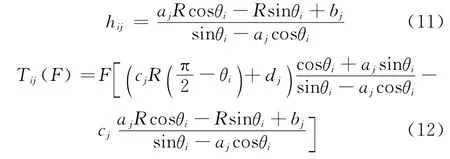
式中：i为转向点或锚固点截面编号；j为相邻转向点或转向点与锚固点之间体外钢束编号.如Tij表示i号截面j号体外钢束一侧的扭矩，hij表示i号截面j号体外钢束一侧的径向偏距.体外预应力抗扭设计流程如图5所示，其中：B为箱梁箱内净宽，p为外荷载，上标＊表示最优解.

图5 体外预应力抗扭设计流程Fig.5 Torsion-resistant design process of applying external tendons

3.2 示例

某单跨曲线箱梁桥如图6所示，曲率半径R＝40m，支座布置为固定（B1）、径向滑动（B2）、多向滑动（B3）、切向滑动（B4）.跨内设置3道转向点，由结构对称性取右半边，选取3个控制截面（图7）：转向点2截面（i＝1）、转向点1截面（i＝2）、锚固截面（i＝3），对应的圆心角θ1＝90.0°，θ2＝75.4°，θ3＝68.5°.采用单箱单室截面（图8），箱内净宽B＝3.6m.

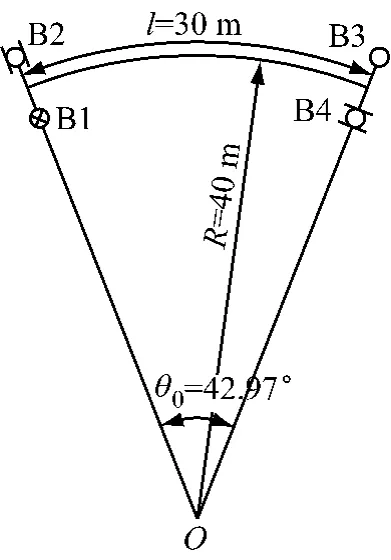
图6 曲线梁总体布置Fig.6 Layout of curved girder

采用Midas Civil软件计算外荷载（自重）作用下主梁内力，得到控制截面的外荷载扭矩T1（p）＝0 kN·m，T2（p）＝3 801kN·m，T3（p）＝4 484kN· m；根据主梁弯矩、剪力设计预加力F＝34 000kN，钢束立面布置如图9所示，钢束立面参数c1＝0，c2＝0.15，d1＝-0.739 6，d2＝-2.269 6.

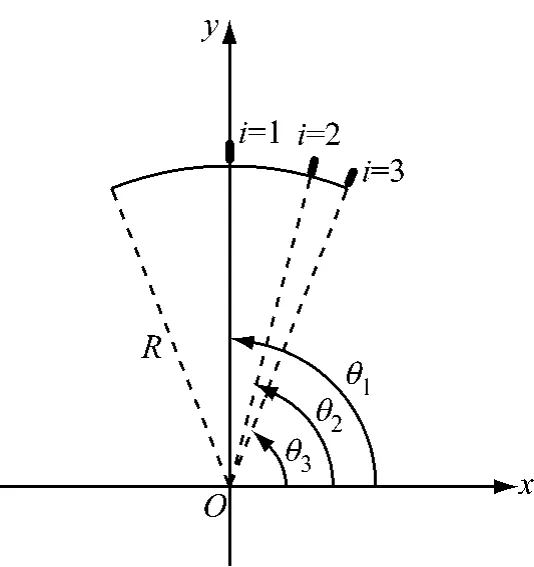
图7 控制截面位置Fig.7 Locations of control sections

图8 箱梁截面（单位：cm）Fig.8 Box-girder section（unit：cm）

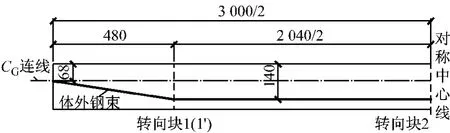
图9 钢束立面布置（单位：cm）Fig.9 Elevation layout of prestressing tendons（unit：cm）

将上述参数值代入式（11）、式（12），可得含参数［a1a2b1b2］的控制截面预应力扭矩T11（F），T21（F），T22（F），T32（F）和径向偏心距h11，h21，h22，h32，可得目标函数如下：

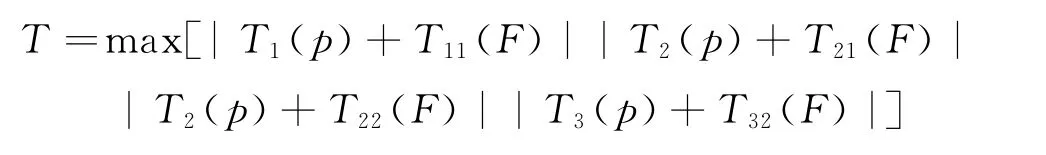
上式同为含参数［a1a2b1b2］的函数，利用MATLAB软件中fminimax函数对其进行非线性规划如下：

得到钢束平面参数的最优解为a＊1＝-0.051，a＊2＝-0.036，b＊1＝38.632，b＊2＝38.485，对应的目标函数为T＊＝1 262kN·m，对应的3个控制截面的径向偏心距为h＊1＝-136.2cm，h＊2＝-60.2cm，h＊3＝77.7cm.

4 分析和比较

4.1 有限元模型

为了说明和验证体外预应力抗扭方法的有效性和扭矩计算公式的正确性，采用有限元软件进行数值分析，模型的设计资料同上示例，模型中预加力和立面布置相同（图8），平面布置如下.

体内钢束模型（IM）：钢束在两侧腹板内，内外侧对称与梁轴线平行布置（图10a）.

体外钢束模型1（EM 1）：钢束在跨中偏移至最内侧，在支点偏移至最外侧布置（图10b）.

体外钢束模型2（EM 2）：钢束平面线形参数根据上述示例中的最优解布置（图10c）.

图10 钢束平面布置（单位：cm）Fig.10 Plane layout of prestressing tendons（unit：cm）

4.2 弯矩与剪力

图11为自重和预应力共同作用下的弯矩图，单元内力值读取位置为单元中点.由于钢束立面布置相同，各模型弯矩分布规律相同，全梁均承受负弯矩，最大负弯矩位于钢束起弯处，峰值相差6%以内.图12为自重和预应力共同作用下的剪力图.各模型剪力分布规律也相同，最大剪力位于钢束起弯处，峰值相差10%以内.综上，IM和EM 1，EM 2的抗弯、抗剪能力相差10%以内，基本相同.

图11 自重和预应力共同作用下弯矩Fig.11 Bending moment under gravity and prestressing

图12 自重和预应力共同作用下剪力Fig.12 Shear under gravity and prestressing

4.3 扭矩

图13为自重和预应力分别作用下的扭矩图.在自重作用下，跨内扭矩向两端的抗扭支承上累积，绝对值逐渐增加，在两支点处达到峰值（4.48×103kN·m）.IM由于钢束对称布置，有h＝h′＝0，预应力作用下理论上应不产生扭矩，但由于外侧钢束预应力损失较大，预加力合力产生与自重作用同方向的扭矩，但绝对值较小（0.40×103kN·m）；EM 1和EM 2由于钢束在跨中内移、在支点处外移，预应力作用下产生与自重作用下相反的扭矩，EM 1在支点处达到峰值（-7.08×103kN·m），EM 2在转向点1处达到峰值（-5.06×103kN·m）.

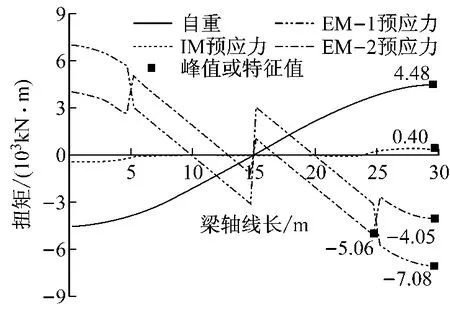
图13 自重和预应力分别作用下的扭矩Fig.13 Torsion moment under gravity or prestressing

自重和预应力共同作用下的扭矩见图14.IM由于预应力产生的扭矩与自重作用下的扭矩方向相同，扭矩峰值增大为4.9×103kN·m；EM 1由于钢束在跨中截面转角较大，扭矩突变较大，出现扭矩峰值为3.30×103kN·m，减幅达到29%，有一定抗扭效果；EM 2近支点处预应力和自重扭矩基本抵消，全跨扭矩峰值为-1.31×103kN·m，减幅达到71%，扭矩分布较均匀，抗扭效果明显，与示例中最优解对应的扭矩峰值（1.26×103kN·m）相比相差4%，结果吻合较好.

4.4 支座反力

自重和预应力共同作用下的支座反力见表1.从表中可知，IM与EM 1，EM 2竖向反力基本相同，反力差相差3%以内，预应力二次力较小；EM 1和 EM 2径向反力明显增大，这是由于体外钢束在梁端的径向集中力作用使梁端发生径向位移，在有径向约束的内侧支座处产生次反力.

图14 自重和预应力共同作用下的扭矩Fig.14 Torsion moment under gravity and prestressing

表1 自重和预应力共同作用下的支座反力Tab.1 Support reaction under gravity and prestressing kN

4.5 扭矩解析解与有限元分析对比

根据式（11）可分别计算得EM 1，EM 2各截面上TP（F），TS（F）和T（F），由钢束平面、立面布置图可得所需参数如表2所示.

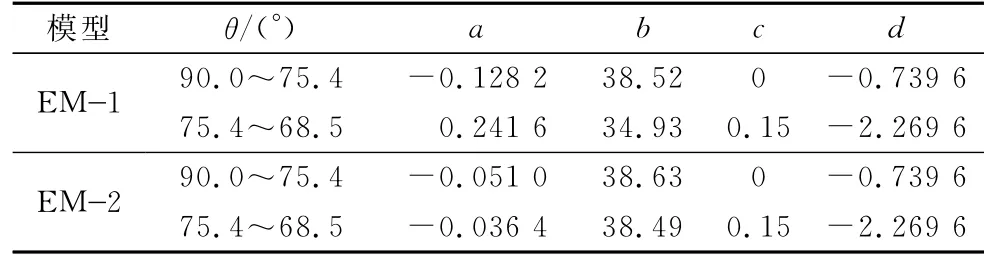
表2 体外预应力扭矩计算公式参数Tab.2 Parameters of externally prestressing torsioncalculation formulas

图15 预应力作用下扭矩Fig.15 Torsion moment under prestressing

根据上表参数，得到EM 1和EM 2中T（F）如图15所示，公式计算结果T（F）和有限元分析结果T0（F）曲线基本重合，吻合较好，造成二者略有偏差的原因为：①T0（F）中计入预应力二次力对扭矩的影响；②T0（F）按单元中点输出，T（F）按圆心角计算，二者位置不一定相同.

对图15进行分析：①转向点1至1′段.由于钢束立面上没有起弯，z′为零，故TS（F）为零，T（F）均由TP（F）提供，大小与h′成正比；②转向点1（1′）截面.钢束竖向起弯和平弯，TS（F）和TP（F）出现突变，EM 1较EM 2平弯转角较大，故TP（F）突变量较大；EM 1，EM 2立面线形相同，竖向分力Fz′s相同，但EM 1竖向分力Fz′s的力臂h绝对值较大，故TS（F）突变量也较大；③转向点1（1′）至锚固点段.预加力作用点立面上不断接近CG线（图9），z绝对值不断减小，TP（F）绝对值也随之减小（EM 1，EM 2分别由12.12和5.49减至1.12和0.67）；钢束平面上穿越CG线，导致h变号，故TS（F）也随之变号（EM 1，EM 2分别由6.72和2.88变为-5.97和-3.47）；④锚固点截面.T（F）主要由TS（F）提供，EM 1，EM 2的z′相同，TS（F）与h成正比，而EM 1中h绝对值较大，故T（F）绝对值较大.

5 结论

（1）由于体外钢束位于混凝土箱梁截面外，具有可大范围空间灵活布置的优势，能起到同时抵抗弯矩和扭矩作用，在抗扭方面与体内钢束相比效率更高、用料更省.

（2）基于体外预应力扭矩计算公式，按照体外预应力抗扭设计流程，经非线性规划可得到曲线箱梁体外钢束平面线形参数的最优解，按此最优解进行钢束平面布置，可以实现全梁扭矩峰值的最小化.

（3）对3种布束方式的单跨曲线箱梁有限元分析的结果表明：与常规对称布束相比，采用优化后的体外钢束抗扭设计可在基本不影响抗弯、抗剪能力情况下大幅降低主梁扭矩的峰值，抗扭效果明显，且与最优解对应的扭矩峰值吻合较好；验证了扭矩计算公式的正确性，公式计算结果与有限元分析结果吻合较好.

［1］ 刘钊.桥梁概念设计与分析理论［M］.北京：人民交通出版社，2010.LIU Zhao.Conceptual design and analytical theory of bridges［M］.Beijing：China Communications Press，2010.

［2］ Nutt，Redfield，Valentine，et al.Development of design specifications and commentary for horizontally curved concrete box-girder bridges［M］.Washington D C：Transportation Research Board，2008.

［3］ 邵容光，夏淦.混凝土弯梁桥［M］.北京：人民交通出版社，1994.SHAO Rongguang，XIA Gan.Curved concrete girder bridge［M］.Beijing：China Communications Press，1994.

［4］ 惠卓，秦卫红，赵金石，等.一种预应力曲线梁新型布筋形式的试验研究［J］.土木工程学报，2011，44（1）：121.HUI Zhuo，QIN Weihong，ZHAO Jinshi，et al.Experimental study on a new type of tendon layout in prestressed curved girders［J］.China Civil Engineering Journal，2011，44（1）：121.

［5］ 梁甜甜.曲线梁预应力效应试验研究［D］.重庆：重庆交通大学，2009.LIANG Tiantian.Test and research on pre-stressed effect about curved grider［D］.Chongqing：Chongqing Jiaotong University，2009.

［6］ 江斌，张鲲，胡杜林，等.预应力设置方式对曲线梁桥扭矩的影响［J］.合肥工业大学学报：自然科学版，2011，34（11）：1706.JIANG Bin，ZHANG Kun，HU Dulin，et al.Influence of prestressing tendon layout on torsion moment of curved beam bridge［J］.Journal of Hefei University of Technology：Natural Science Edition，2011，34（11）：1706.

［7］ 李建慧，宋旭明.独柱支承预应力连续弯箱梁扭矩调整［J］.黑龙江工程学院学报，2003，17（1）：21.LI Jianhui，SONG Xuming.The adjustment of torsion moment for single-column supported continuous curved prestressed beam bridge［J］.Journal of Heilongjiang Institute of Technology，2003，17（1）：21.

［8］ 杨永贤.小半径预应力混凝土曲线梁桥抗扭设计方法探讨［J］.公路交通技术，2010（5）：45.YANG Yongxian.Discussion on torsion-resistant design method for small-radius curved prestressed concrete girder bridges［J］.Technology of Highway and Transport，2010（5）：45.

［9］ 杨孟刚，陈庚.大跨度曲线刚构桥预应力设置对扭矩的影响［J］.桥梁建设，2011（3）：15.YANG Menggang，CHEN Geng.Influence of prestressing tendon layout on torsion moment of long span curved rigidframe bridge［J］.Bridge Construction，2011（3）：15.

［10］ 李新平，任华.曲线箱梁桥预应力作用的仿真分析［J］.华南理工大学学报：自然科学版，2005，32（12）：47.LI Xinping，REN Hua.Simulation analysis of the prestressing effect on the curved box girder bridge［J］.Journal of South China University of Technology：Natural Science Edition，2005，32（12）：47.

［11］ 陈宏，姜峰，赵伟.预应力钢束布置形式在混凝土曲线梁桥中受力性能分析［J］.科技资讯，2011（21）：66.CHEN Hong，JIANG Feng，ZHAO Wei.Performance analysis of the prestressing tendon layout in curved concrete girder bridges［J］.Science and Technology Information，2011（21）：66.

［12］ Salse E A B.Analysis and design of prestressed concrete circular bow girders for bridge structures［C］∥Second International Symposium on Concrete Bridge Design ACI.Defroit：American Concrete Institute，1969：714-740.

Torsion-resistant Design in Curved Box-girder Bridges with External Tendons

SHEN Yin，SONG Taiyu，LI Guoping
（College of Civil Engineering，Tongji University，Shanghai 200092，China）

In order to resist torsion effect to improve the stress state in curved box-girder bridges，the torsion-resistant design method of applying external tendons without increasing tendons is proposed.Based on the space analytic geometry relationship，the externally prestressing torsion calculation formulas are derived out.The torsion-resistant design process of applying external tendons is presented with the objective of minimizing torsion.The optimal parameters of horizontal alignment of tendons are solved with non-linear optimization method at the end of the process.The results indicate that the reasonable space layout design of external tendons instead of internal tendons significantly reduces peak torsion，and has almost no impact on the bending and shearing capacity.Comparison with the finite element analysis shows that the numerical results calculated by the formulas agree well with the finite element analysis，therefore the formulas can be a simple approach for practical design.

curved box girder；prestressing torsion；space analytic geometry；non-linear optimization

U442

A

0253-374X（2015）12-1777-07

10.11908／j.issn.0253-374x.2015.12.002

2014 10 26

国家自然科学基金（51208376）

沈 殷（1977—），女，讲师，工学博士，主要研究方向为预应力混凝土.E-mail：shenyin@tongji.edu.cn

宋泰宇（1990—），男，博士生，主要研究方向为混凝土弯梁桥.E-mail：13585562901@163.com