基于螺旋理论对4-UPU并联机构的自由度及运动分析*

2015-01-15胡兴伟夏广岚殷宝麟孙赵宁庄腾飞

现代机械 2015年2期

胡兴伟，夏广岚，殷宝麟，于峰，孙赵宁，庄腾飞

(佳木斯大学机械工程学院，黑龙江佳木斯 154007)

与串联机器人相比，并联机器人具有许多优点，而近年来对少自由度并联机构的研究已成为了一个热点［1-3］。因为少自由度并联机器人由于其结构简单、驱动容易、造价低而具有较高的实用价值，在实际中有广泛的应用前景［4-7］。

本文研究的少自由度并联机构在空间能实现三移动一转动，它是由上下平台以及四个分支链构成。四个支链的结构均对称分布，且每个支链都由一个虎克铰，一个移动副，一个虎克铰组成，下平台为静平台，上平台为动平台。本文应用螺旋理论［8］对4-UPU并联机构进行了自由度分析，最终成功验证了该并联机构的自由度为4。

1 自由度分析

1.1 螺旋理论基本知识

在几何数学中，一条空间直线的姿态(位置和方向)是由两个点来确定的。在螺旋理论的范畴里，如图1所示，空间任何一条直线的确定是由方向矢量S和矢量S对原点的线矩S0来定义表示的，直线也叫做线矢量(节距h=0)，是旋量一种特殊的情况。直线的的矢量表达形式如下:

其矢量方程的标准形式即为:

齐次坐标满足:

图1 直线的矢量方程

其中L、M、N是有向线段 S的方向数，P、Q、R是该线段S对原点的线矩在X、Y、Z三轴的分量。当S·S=1时，则线矩S0的模表示直线到原点的距离。此时ξ为单位线矢量;当S0=0时，即直线的线矩为零，此时直线经过原点。由表达式显然可知，S·S0=0。这种满足正交条件的齐次坐标(S;S)0表示了直线在空间的方向及位置，(S;S)0称为直线的Plücker线坐标。

若节距∞≠h≠0，且 S·S0=0，S≠0 时，用 h=S·S0/S·S来表示该旋量的节距。那么该旋量可以看作是一个线矢量与一个偶量的同轴合成，即为:

若节距 h=0，S·S0=0，S≠0时，旋量就退化为线矢量，此时可以用来表示一个转动副或者一个约束力;若S=0，S0≠0时，则旋量退化为偶量，即为(0;S0)，此时的节距为无穷大，那么该旋量可以表示一个移动副和约束力偶。

若 ξ1，ξ2分别为(L1，M1，N1;P1，Q1，R1)与(L2，M2，N2;P2，Q2，R2)，则两个螺旋的互易积定义如下:

如果所研究的两个螺旋ξ1，ξ2之间的互易积为零，即为:

在这里称与螺旋1构成互易积为零的螺旋2为螺旋1的反螺旋。可以从物理的运动及力的角度解释，可以把ξ1看作力螺旋，ξ2看作是运动螺旋，在如上表述的情况下，无论该力螺旋的力及力矩多大，都无法对物体进行做功，不影响物体的运动形态，也不改变物体在约束允许下的螺旋运动。为了更加清晰的来描述螺旋与反螺旋的定义，不妨设ξ=(S;S0)和，那么可以表示如下:

通过上述等式，对于运动螺旋ξ的反螺旋ξr，若是它的节距为零，则代表一个约束力，其限制了沿约束力方向的移动;若是它的节距为无穷大，则代表一个约束力偶，限制了绕该力偶方向的转动。

当两个螺旋的互易积为零时，如果一个螺旋表示了机械系统的约束反力，另一个则是为该机械系统所允许的运动;反之，如果一个螺旋表示了物体的运动，另一个则是机械系统本身所产生的约束。

两螺旋互易积为零的解析式还可以表示为:

可见，若ξ为ξr的反螺旋时，同理ξr也一定为ξ的反螺旋，这正是反螺旋的互逆性的定义。两个互逆的螺旋的互逆性和线性相关性只与两个螺旋自身的参数有关，与原点的位置无关，也即与坐标系的选择没有任何联系。因此在分析某些机构尤其是少自由度并联机构的自由度时，一般可以从以下几个步骤来完成:

1)对于对称型并联机构，首先建立适当的坐标系，根据各支链的运动副分布情况及属性写出某一支链相对应的各运动副的螺旋;对于非对称性的并联机构，支链相同的可以只写出一个支链中的各个运动副的螺旋，不同的支链应分别列写出各支链相对应的运动副螺旋即可;

2)根据线性代数理论，若线性方程组有n个未知数，方程组系数矩阵的秩为r，根据具体情况进行求解，若n＞r和n＜r时，在无穷多个解向量中，解向量之间最大的线性无关的数目为n-r，这样由互逆螺旋线性方程决定的基础解析将会有n-r个螺旋构成，这也是最大的线性无关的反螺旋数目。

3)通过分析该并联机构的阶数、构件数、运动副的数目等一系列相关的参数后，那么利用修正后的 Kutzbach-Grüber公式［4］便可以计算机构的自由度。

1.2 4-UPU机构的自由度计算

修正后的Kutzbach-Grüber公式为:

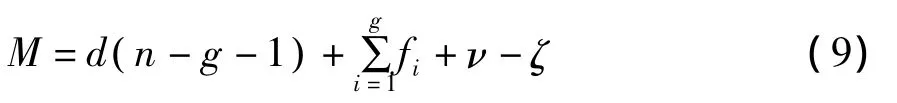
在公式中，其中M表示机构的自由度;d表示机构的阶数，机构的阶数由公共约束数来确定;n表示所有的构建数目;g表示机构中的运动副数目;fi表示第i个运动副的自由度数目;ν为多环并联机构在去除公共约束的因素后的冗余约束的数目;ζ为机构中存在的局部自由度。

如果4-UPU机构的动、静平台不为正方形时，根据4-UPU并联机构的结构形式以及排列组合的原理可以得到24种不同的结构组合形式。在这里只对4条支链的两端均采用虎克铰垂直布置的结构形式进行分析验证。该并联机构的4条支链的各运动副布置情况的具体结构如图2所示。

图2 4-UPU并联机构(虎克铰垂直布置)结构图

从图中可以看到该结构的链接布置情况，与静平台相链接的为虎克铰 ai(i=1，2，3，4);与动平台相链接为虎克铰 bi(i=1，2，3，4)。四个支链的结构对称，均由虎克铰-移动副-虎克铰的形式进行链接。建立下平台静坐标系OB-XBYBZB，点OB位于下平台的质心点，XB轴平行于a1a4，同理YB轴平行于a1a4，Zb轴垂直于下平台向上。建立机构的动平台坐标系OM-XmYmZm，其中点OM位于上平台的质心点，Xm轴平行于b1b2，v轴平行于b1b4，ZM轴垂直于上平台向上。由于一个虎克铰副等效于两个轴线互相垂直相交的转动副(即U=2R)，在此定义其中一个R垂直于定平台，另外一个R则平行于静平台。

由于四条支链完全对称，因此可以选择研究其中任何一条支链即可。其中给予以下结构位置参数，(p q 0)为下平台虎克铰的中心位置，(i j k)为移动副的方向余旋，(l m n)为上平台虎克铰的中心位置。那么根据所给出的位置参数，可以写出4-UPU并联机构第一支链的螺旋表示:

根据互易积计算公式ξi·ξi(r)=0，可以求得该支链的一个反螺旋为:

通过计算结果可以清晰地看出ξi(r)为一个反螺旋力偶，其实它的存在限制了动平台绕X轴的转动，因此根据结构的完全对称型知道四个支链均有相同的反螺旋力偶，根据高等空间机构学Grassmann线几何原理，该并联机构的4个反螺旋不能构成公共约束，并且仅有2个是线性无关的，那么d=6，υ=t-k=2，再看结构布置图2，该并联机构不存在局部自由度，因此 ζ=0，根据修正后的 Kutzbach-Grüber公式(9)计算如下:

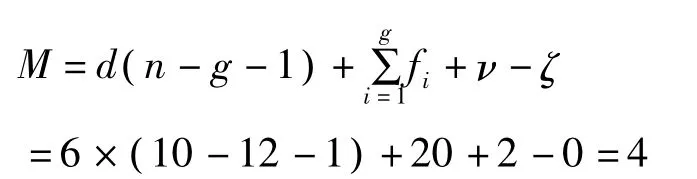
由计算结果可知，该并联机构的自由度数为4。

2 4-UPU运动分析

通过上面基于螺旋理论及Kutzbach-Grüber公式对4-UPU型并联机构的自由度进行了验证并取得了正确的结果值。可以从其螺旋的位置及方向可以确定动平台可以实现3T1R，针对该机构的结构特点及动平台的位姿给出的详细描述，然后可以顺利地构造出其运动学模型，并得到以下结论:

动平台绕z轴的转动和沿x、y、z三坐标轴的移动，该机构属三移动一转动自由度机构。通过初步建立4-UPU并联机构的模型，并基于Pro/E中MDX模块对所实现的运动做了一个仿真。下面给出了机构的运动示意图，其中的图3给出了动平台相对于静平台沿x轴方向的移动，图4给出了动平台相对于静平台沿y轴方向的移动，图5给出了动平台相对于静平台沿z轴方向的移动，图6则给出了动平台相对于静平台沿z轴方向的转动。