一个n阶本原有向图的m-competition指数

刘彩锋，高玉斌

(中北大学 数学系，山西 太原 030051)

一个n阶本原有向图的m-competition指数

刘彩锋，高玉斌

(中北大学 数学系，山西 太原 030051)

文中讨论了一个含有一个n-2圈和一个n-3圈的n阶本原有向图D.由D的结构得到本原图Dn-2和Dn-3, 然后分别对本原图D, Dn-2和Dn-3中任一点经过k长途径所到达的顶点的集合以及顶点的个数进行分析, 再结合m-competition指数的定义, 得到这个本原图的m-competition指数.

有向图; 本原图; m-competition指数

1 预备知识

近年来, 本原有向图的scrambling指数和m-competition指数是学者们的一个新兴研究分支.2009年,Akelbek和Kirkland在文献[2]中提出了本原有向图的scrambling指数的概念.2010年, Hwa Kyung Kima将本原图的本原指数和scrambling指数推广到m-competition指数(也叫广义competition指数), 并在文献[3]中给出m-competition指数的定义, 随后, 他找到了本原矩阵的m-competition指数的上界, 同时确定了最小圈长为s的本原图的m-competition指数的上界, 而文中讨论了一个特殊本原有向图的m-competition指数.

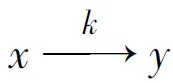
定义1[2]设D为n阶有向图, 如果存在正整数m, 使得对于D中任意两点x,y, 从x到y都有m长的途径, 则称D为本原有向图, 或称本原图.

有向图D是本原图的充要条件是D为强连通图且D中所有圈长的最大公因子为1[1].如果D为本原图, 则Dl也为本原图.D为强连通图是指D为有向图且任意顶点u,v∈V(D), 既存在u到v的途径, 又存在v到u的途径[1].

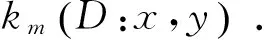
文中符号N+(Dk:x)表示点x在D中经过k长途径所到达点的集合, |N+(Dk:x)|表示集合中顶点的个数.N+(Dk:x,y)表示顶点x和y在D中经过k长途径所到达公共点的集合, 即N+(Dk:x,y)=N+(Dk:x)∩N+(Dk:y).

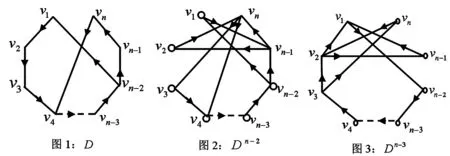
设D为一个本原图, C为D中的一个圈, 则用l(C)来表示C的圈长.文中本原有向图中的顶点上的小圆圈表示一个环, 即该顶点是一个环点, 环的方向可以任意, 既可以顺时针也可以逆时针.

2 主要定理及证明

定理设n阶(n≥12)本原图D如图1所示，D中含有一个n-2圈和一个n-3圈,

则对于正整数m(1≤m≤n), D的m-competition指数为

证明 情形1 1≤m≤n-5且n+m为奇数.

子情形1 对任意x,y∈V(D)且x,y≠vn-3和vn-4时,存在vi,vj∈V(D)(4≤i,j≤n-2),

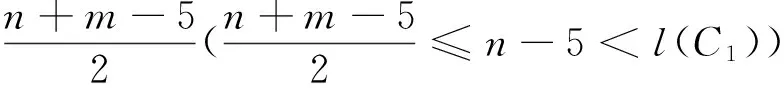
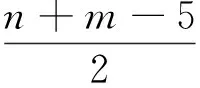
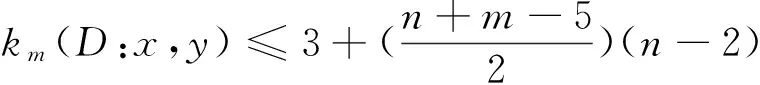
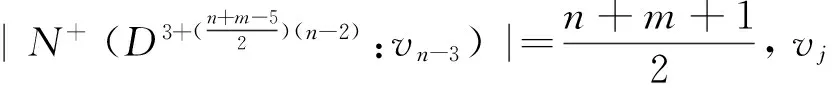
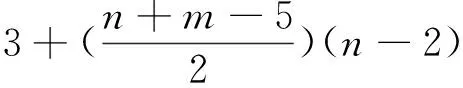
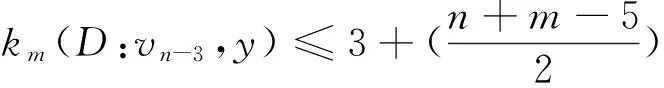
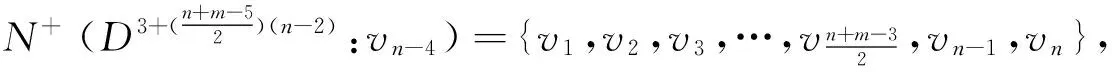
(2)

子情形3 当x,y等于vn-3和vn-4时, 不妨设x=vn-3,y=vn-4时, 由上(1)(2)式可得

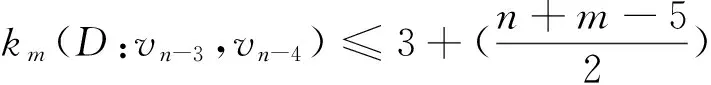
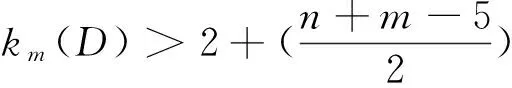
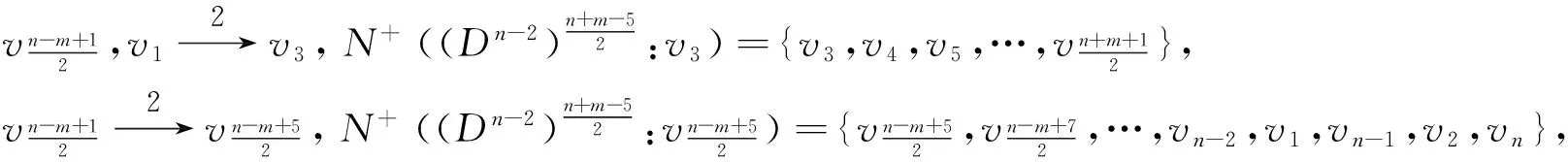
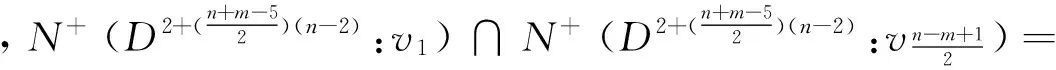
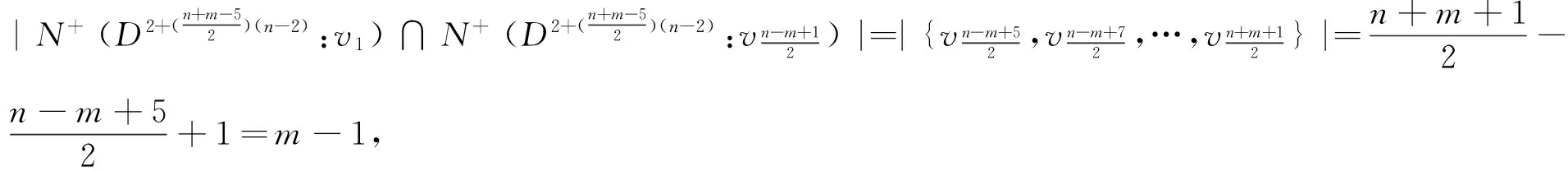
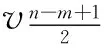
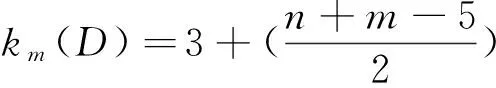
情形2 1≤m≤n-4且n+m为偶数.

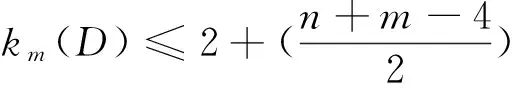
子情形1 对任意x,y∈V(D)且x,y≠v1,vn-3,vn-2, 存在vi,vj∈V(D), 其中

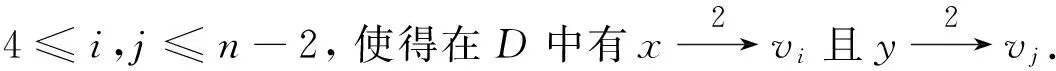
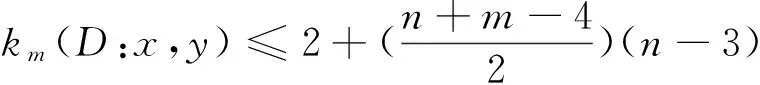
子情形2 对任意x,y∈V(D)且x,y中有一个等于v1或vn-3或vn-2时, 不妨设x=v1,

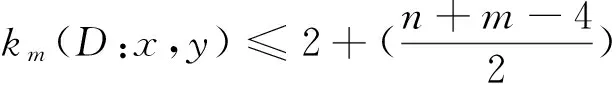
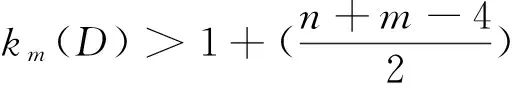
在Dn-3中取特殊点v1和

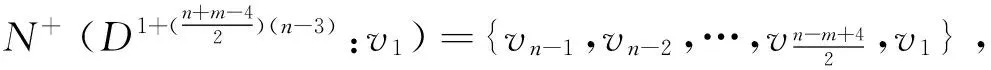
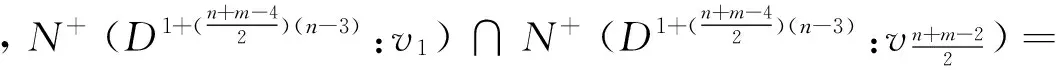
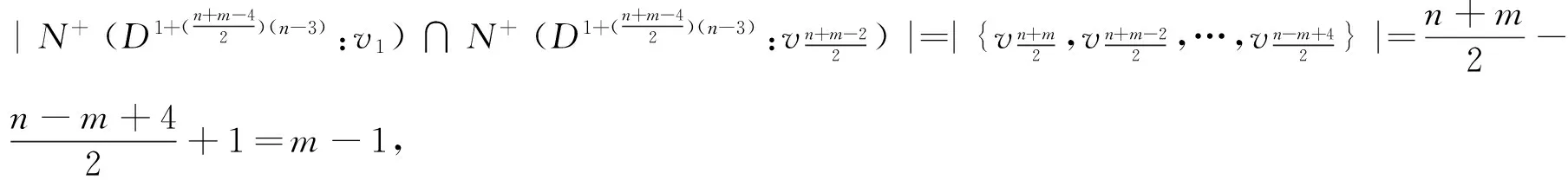
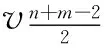
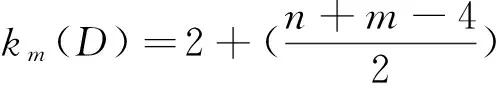
情形3 m=n-3.

在Dn-2中, N+((Dn-2)n-4:v1)=V(D){vn-2},N+((Dn-2)n-4:v2)=V(D){v1,vn-1},

N+((Dn-2)n-4:v3)=V(D){v2,vn}, N+((Dn-2)n-4:v4)=V(D){v3},

N+((Dn-2)n-4:vj)=V(D)(5≤j≤n-2), N+((Dn-2)n-4:vn-1)=V(D){v1,vn-1},

N+((Dn-2)n-4:vn)=V(D){v2,vn}.

即在D中,N+(D2+(n-2)(n-4):v1)=V(D){v2,vn},N+(D2+(n-2)(n-4):v2)=V(D){v3},

N+(D2+(n-2)(n-4):vi)=V(D)(3≤i≤n-4),

N+(D2+(n-2)(n-4):vn-3)=V(D){vn-2}∪V(D){v1,vn-1}=V(D),

N+(D2+(n-2)(n-4):vn-2)=V(D){v1,vn-1}∪V(D){v2,vn}=V(D),

N+(D2+(n-2)(n-4):vn-1)=V(D){v3}, N+(D2+(n-2)(n-4):vn)=V(D).

则任意x,y∈V(D), 在D中经过2+(n-2)(n-4)长途径至少含有n-3个公共点, 从而kn-3(D:x,y)≤2+(n-2)(n-4).

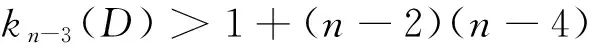
N+(D1+(n-2)(n-4):v1,v2)=V(D){v1,vn-1}∩V(D){v2,vn}=V(D){v1,v2,vn-1,vn},

即在D中v1和v2经过1+(n-2)(n-4)长途径所含公共点个数小于n-3, 从而

kn-3(D)>1+(n-2)(n-4). 综上所述kn-3(D)=2+(n-2)(n-4).

情形4 m=n-2.

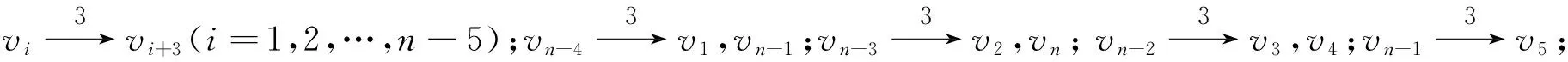
kn-2(D:x,y)≤3+(n-2)(n-4).

下面证kn-2(D)>2+(n-2)(n-4).

取特殊点

V(D){v3}, 所以N+(D2+(n-2)(n-4):v1,v2)=V(D){v2,vn}∩V(D){v3}=V(D){v2,v3,vn}, 即在D中v1和v2经过2+(n-2)(n-4)长途径所到达的公共点的个数小于n-2, 从而kn-2(D)>2+(n-2)(n-4). 综上所述

kn-2(D)=3+(n-2)(n-4).

情形5 m=n-1.

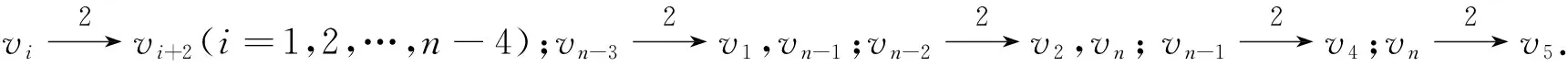
在Dn-3中,N+((Dn-3)n-3:v1)=V(D){v1,vn-1},N+((Dn-3)n-3:v2)=V(D){v2,vn},

N+((Dn-3)n-3:v3)=V(D){v3}=N+((Dn-3)n-3:vn),

N+((Dn-3)n-3:vj)=V(D)(4≤j≤n-2), N+((Dn-3)n-3:vn-1)=V(D){v2,vn}.

即在D中, N+(D2+(n-3)(n-3):v1)=V(D){v3},

N+(D2+(n-3)(n-3):vi)=V(D)(2≤i≤n-4),

N+(D2+(n-3)(n-3):vn-3)=V(D){v1,vn-1}∪V(D){v2,vn}=V(D),

N+(D2+(n-3)(n-3):vn-2)=V(D){v2,vn}∪V(D){v3}=V(D),

N+(D2+(n-3)(n-3):vn-1)=V(D)=N+(D2+(n-3)(n-3):vn).

则任意x,y∈V(D), 在D中经过2+(n-3)(n-3)长途径至少含有n-1个公共点, 从而kn-1(D:x,y)≤2+(n-3)(n-3).

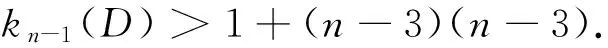
即在D中v1经过1+(n-3)(n-3)长途径所到达的点的个数小于n-1, 从而

kn-1(D)>1+(n-3)(n-3). 综上所述kn-1(D)=2+(n-3)(n-3).

情形6 m=n.

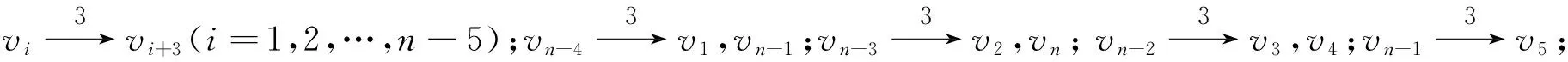
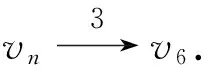
kn(D:x,y)≤3+(n-3)(n-3).

下面证kn(D)>2+(n-3)(n-3).

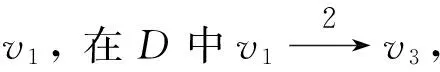
[1] Brualdi R A, Ryser H J.Combinatorial Matrix Theory [M].Cambridge University Press, 1991.

[2] Liu B L, Huang Y F.The scrambling index of primitive digraphs[J].Computers and Mathematics with Applications, 2010, 60(3):706-721.

[3] Kim H K.Generalized competition index of a primitive digraph [J].Linear Algebra and its Applications,2010, 433 (1):72-79.

[4] Akelbek M, Kirkland S.Coefficients of ergodicity and the scrambling index [J].Linear Algebra and its Applications,2009,430(4):1111-1130.

[5] Shao Y L, Gao Y B.The m-competition indices of symmetric primitive digraphs with loop[J].Ars Combination, 2013, 108:217-223.

[责任编辑：王军]

The m-competition index of a primitive digraph of order n

LIU Caifeng,GAO Yubin

(Department of Mathematics, North University of China, Taiyuan 030051,China)

In this paper, a primitive digraph D of order n with one (n-1)-cycle and one (n-2)-cycle is considered.According to the structure of D, we draw up the primitive digraphsDn-2andDn-3.Then the sets and the numbers of vertexes, which are formed by each vertex passing a walk of length k in the primitive digraphs D, Dn-2and Dn-3are discussed respectively.In addition, based on the definition of m-competition index, we work out the m-competition index of the primitive digraph.

digraph; primitive digraph; m-competition index

2015-01-12

国家自然科学基金资助项目(11071227)；山西省回国留学人员科研资助项目(2012-070)

刘彩锋(1988-)，女，山西吕梁人，中北大学硕士研究生，主要从事组合数学的研究.

高玉斌(1962-)，男，中北大学理学院教授，博士生导师，主要从事组合数学的研究.

O157.5

A

1672-3600-(2015)09-0001-06