引领实践操作发展空间观念

◎福建省诏安县实验小学林华

引领实践操作发展空间观念

◎福建省诏安县实验小学林华

小学数学操作课因其积极作用的目益彰显而倍受关注。实践操作能充分发挥学生在学习中的主体地位，在折折、拼拼、剪剪等实践操作活动中，培养和发展学生的空间观念。让学生在自主探索中，建立表象，在合作操作中形成认识，在拓展操作中实现升华，从而达到培养和发展学生的空间观念及想象能力的目的。

实践操作；空间观念；拓展观念

小学生对新鲜事物特别感兴趣，凡事都想动手试一试。这种好奇好动的心理特征，决定了枯燥无味的说教远不如实践操作对学生学习的作用明显。但实践操作不能简单地理解为让学生“动手”，实际上是借助学生的亲自动手，协调多种感官的作用，并和思维活动紧密结合以获得更佳的预期效果的一种学习方式；因而它是破解数学的高度抽象性和严密逻辑性这一学科特点行之有效的方法。操作课能让学生的实践操作能力和空间想象能力得到充分的训练和发展。极大地提高了学生数学学习的有效性。本文就关注小学生动手实践操作对发展学生的空间想象能力的影响，谈谈自己在教学实践中的探索与体会。

一、自主操作，建立表象，发展空间观念

操作课是调动学生手、眼、口、耳等多种感官参与认知活动的一种学习方式。让学生自主实践操作学具，通过画一画、折一折、剪一剪、拼一拼等操作活动。帮助学生获得直接具体的感性认识，借助操作与想象的有机结合，使学生初步建立起较清晰鲜明的表象，进而发展学生的空间观念，培养学生的抽象思维能力。例如，在教学“圆柱体侧面积”计算公式时，教师课前先让学生寻找几个外贴一圈商标纸的圆柱体空食品罐，新课伊始，教师让学生用手摸一摸侧面，感受侧面积的位置与大小，让学生讨论如何知道侧面积的大小。学生议论纷纷，有学生说：“看看这张纸有多大，侧面积就有多大？”另一学生随口说：“那不如把圆柱的侧面积直接展开看看大小。”……教师抓住时机：“这位同学的方法很好，把你们手中的商标纸展开看看，能不能求出它的面积？”学生带着问题，以小组为单位，自主操作、思考，同学们都兴趣盎然地进行了“破坏”与重新“组合”。教师找出几个有代表性的，如：“斜着剪”的、“撕成不规则状”的、“沿着高剪开”的进行展示。让学生通过观察得出：圆柱的侧面展开图可能是多种图形。拿出沿着“高”剪开的情况，让学生在操作活动中自主探索长方形的长和宽与圆柱的底面周长、高之间的关系，在这基础上，引导他们加以归纳。很快就得出圆柱的侧面积计算公式了：S=ch，整个过程让学生在轻松、愉悦、和谐的自主操作中，经历从表象中抽象出圆柱侧面积的计算公式的思维过程，发展了学生的空间观念：面围成体。而且从中积累了解决几何问题的一些策略。有了以上的体验，诸如“有一长20厘米，宽10厘米的长方形纸，围成圆筒后求圆筒的侧面积”的一类题目，学生就迎刃而解了。

二、合作操作，形成认识，发展空间观念

苏霍姆林斯基说过：“手使脑得到发展，使它更加明智；脑使手得到发展，使它变成思维的工具和镜子。”小学生由于刚接触到“体”，空间观念较差，获得的解决问题的策略比较少，特别是由“面”旋转成“体”的问题，他们往往不知从何入手。而发展空间观念的重要途径就是操作、想象、思考相结合。由于每个学生个体在空间想象能力上存在差别，因此加强合作操作，互助互学，有利于学生在理解的基础上探索图形的特征与规律，发展空间观念。

如在教学“圆柱和圆锥”时，教师课前要求学生先做好长方形小旗和三角形小旗（旗杆都用较长木棒做成）。课堂上，由一名学生拿在手上搓玩，同一小组其他学生指出一些重要的点和线，利用视觉暂留效果，仔细观察旗子上每一个点和每条线段在旋转过程中的运动轨迹，思考并猜测：“旋转后可能得到的是何种立体图形？”并展开小组讨论，总结汇报。学生经过搓动、思考、表象、猜测和推理，得出由面旋转成体。让学生将外显的动作过程与内隐的思维活动和谐地结合在一起，空间观念在这过程中逐渐形成了。

基于上述操作思考，教师引领学生解决如下图，求旋转后图形的体积，就得心应手了。教学时，先让学生说出图形的组成部分，化整为零，逐个击破，由学生合作进行搓玩原题的模具，猜测可能得到的图形，教师可出示图形的变化和生成：

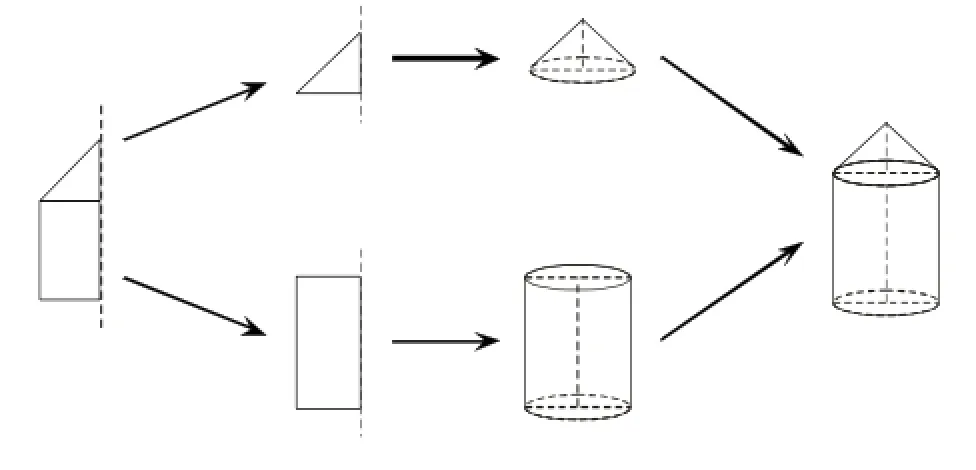
从上述活动中，让学生更清楚地领会图形的变化过程，在合作交流中，让学生运用旧知识，解答新问题，获得新认知。

三、拓展操作，实现升华，发展空间观念

“学以致用”这是古人对学习目的的高度概括。操作为数学学习服务，最终的目的是使学生在学习数学的过程中，获得一定的基础知识和基本技能，形成一定的思维策略和方法，实现空间想象能力的拓展和提高，为学生以后的学习和生活打下坚实的基础。教学中应遵循规律，从学生的经验和已有知识出发，注重拓展延伸，进一步发展他们的能力，使“动作的思维”升华为“思维的动作”，使在实践操作中获得的感性认识，经过思考转化为策略、技能。例如上面所讲到的例子，图①，让学生求出体积后，教师冷不防拔下上图模具的木棒，粘到原旋转轴的对面，即变为图②。先要求学生照样子做，再提出要求：“此图与原来的图有何异同？”（此问题可以让学生利用类比的方法发现新旧问题之间的联系，以旧引新，降低难度）；“现在又可旋转成何种立体图形？”学生又“玩”开了。由于新题上半部分较特殊，学生争论不休，整个课堂沸腾了。

最后小组汇报结果，共有以下几种情况：A、旋转后得到一圆柱体。B、旋转后得到与图②得到的图形一样。C、旋转后应得到一圆柱体上部挖掉一个圆锥体。

教师接着问：“这个图形应该注意哪几个点和哪几条线段的运动轨迹？”学生又开始了新一轮的操作和讨论，最后达成共识：应注意上半部三角形两个锐角的顶点和三角形的斜边。进而让学生再次实物操作，认真观察直角三角形斜边的运动轨迹，最后让学生通过推理、思考得到升华：直角三角形的斜边又旋转成一个圆锥，只不过这个圆锥是虚的。此时教师抓准时机，在图②的左上角添上辅助线：把图补成长方形，再一次出示图形的变化和生成过程。让学生进行第三轮讨论，汇报出结果，选择正确答案C。

在上述环节学习中，以实际操作为手段，让学生在旧知识的基础上，充分展开想象，进行拓展延伸操作，从而达到触类旁通，举一反三，得出解决几何问题的辅助性条件，这实现了以拓展促“升华”的目的，有力地提高了学生的空间想象能力，使学生的空间观念得到较大发展。

综上所述，实践操作能充分发挥学生在学习中的主体地位，让学生在折折、拼拼、剪剪等活动中不知不觉中培养和发展学生的空间观念；让学生在自主探索中建立表象，在合作操作中形成认识，在拓展操作中实现升华，并通过自主地学习，快乐地学习，从而达到培养和发展学生的空间观念及想象能力的目的。

（责任编辑：陈志华）