系统结构缺陷分层预测方法

胡长虹，王鹤琪，韩 啸

(1.中国科学院长春光学精密机械与物理研究所，长春130033;2.吉林大学学报编辑部，长春130012)

0 引 言

计算机及微电子技术在信息技术领域占据核心的主导地位，在工业、农业、航海、航空、航天和人类生存等高技术领域起到关键性作用。特别是近几年，随着软件系统的不断成熟和发展，使互联网络、人工智能、大数据处理、物联网工程、信息传输和图像处理等信息技术得到空前发展。软件技术在这些领域起着主导作用，已经渗透到人类生活的每个角落。在软件开发过程中，软件的质量、开发进度和成本是人们关注的3大要素，其相辅相成，既彼此依赖又互相制约。因此，提高软件质量、缩短软件开发周期和降低软件开发成本是软件的主要研究方向，也是市场急需解决的相关技术问题。

目前，我国的航空、航天、航海、武器对抗、银行和交通等领域的高技术管理获得了高速发展，计算机软件已经在这些领域起到核心作用，成为不可缺少的关键技术，其中很多重大项目都具有软件缺陷不可修复和弥补性(例如国防建设、神舟系列飞船和登月工程等)，国家乃至全世界急需质量稳定、可靠及无缺陷的软件。

目前研究缺陷预测方向的学者主要精力集中于软件的功能或工程师编码过程中的缺陷，而且对这类缺陷预测及修复方法的研究已经十分成熟，极少出现由于这类软件缺陷导致大型工程项目失败的状况。然而在软件系统结构中所出现的缺陷难以发现和准确定位，所以，因软件系统结构缺陷而导致项目失败的情况屡屡发生，如:1)困扰银行金融系统的千年虫问题;2)困扰电脑时钟系统的2038问题。国外针对这类软件系统结构缺陷预测的研究也是凤毛麟角，我国急需针对软件系统结构缺陷预测问题开展专项的研究。

软件缺陷预测大致可分为两类，分别是静态软件缺陷预测技术和动态软件缺陷预测技术。

在静态软件缺陷预测技术中包含基于度量元的缺陷预测、基于软件缺陷分布的缺陷预测技术和基于模型的缺陷预测技术。

1)基于度量元的预测技术［1－3］。基于软件规模的软件缺陷预测方法:该种方法包含7种较典型的缺陷预测模型和标准，如:千行代码出错率(也叫做CMMI标准)［4］、Akiyama模型［5］、谓词模型、Halstead模型［6］、Lipow 模型［7］、Gaffney 模型［8］、Compton and Withrow 模型［9］等。

2)基于软件复杂度的软件缺陷预测方法。该种方法较典型的是20世纪70年代由McCabe＆Associates公司提出的 McCabe Cyclomatic Complexity Metric(圈复杂度)［10］方法。

3)基于软件缺陷分布的预测技术。典型分析方法有:主成分分析(PCA:Principal Component Analysis)［11］、线性判别分析(LDA:Linear Discriminant Analysis)［12］、布尔判别函数(BDF:Boolean Discriminant Function)［13］、聚类分析(CA:Clustering Analysis)［14］、缺陷预测回归分析方法［15］(典型方法:人工神经网络(ANN:Artificial Neural Network))［16］、多元回归分析(MR:Multiple Regression Analysis)［17，18］、基于用例推理(CBR:Case－Based Reasing)［19］等。

4)基于模型的预测技术。典型模型有:COQUALMO(Constructive Quality Model)模型［20－22］、DRE模型［23－26］和贝叶斯网络模型［27－32］。

动态软件缺陷预测技术又称为多目标软件缺陷预测技术，其主要研究方法都是基于模型的，其中较典型的有:Rayleigh 模型［33］、指数分布模型［34，35］和 S 曲线分布模型［36］等。

综上所述，笔者针对缺陷出现的特征及缺陷间的关联关系进行分层分析和研究:第1层使具有相关特征及缺陷特征的跨界缺陷成簇;第2层使具有强关联关系的缺陷簇再次聚集成簇，有利于工程中对软件结构缺陷的发现，同时也有利于相似缺陷的集中修复，避免软件缺陷在修复过程中又引入新的缺陷。

软件系统结构缺陷是指:软件结构间因组合方式不当而导致的系统缺陷，这里的软件结构不仅是模块间的结构组合方式，同时也包含在代码设计过程中出现的结构缺陷。例如:在软件结构设计中过多的反复使用并行结构、串行结构、环形结构、嵌套并行结构、并行嵌套结构和递归循环结构等。

1 分层式缺陷预测模型

一种基于服务评价的最优节点竞争选择模型的研究方法是以分层式数据节点为基础，以用户与数据节点之间的应答式访问模式为主要契机，即用户向任务管理器提出请求由数据节点回复其请求并提供相关服务。其主要特点包括。

1)分层式模型并不采用集中式的预测理念，而从一个全局的角度为切入点逐层进行缺陷预测，每层缺陷预测方法都具有高度的自主权。

2)由于分层式预测模型中的数据冗余，预测数据存在相互复制，使模型的可用与否和数据的准确与否不会因为模型中某个缺陷节点或数据节点的死亡而发生变化。

3)分层式模型中的数据独立性和数据透明性。从外层看，一组数据在分层式模型中的存在是一个整体，所以，外部对数据节点的转移不会影响模型的正确性。

图1 分层式预测结构Fig.1 Hierarchical prediction

图1中第1层为基础预测层主要根据缺陷的特征，使特征相似的节点会聚集成簇。第2层为关联关系预测层以第1层已经预测的缺陷簇为基础，通过对关联关系系数及缺陷权重等参数的计算，得到缺陷簇间的关联关系强度，使具有强关联关系的缺陷簇再次成簇，并进行预测。

2 缺陷特征预测方法

在多数的软件项目中，软件缺陷常常发生在不同条件下。缺陷有时可能发生在同一项目中，所以，需要依据软件缺陷的不同，酌情分配不同的特征。例如，在某个航天项目中，有两个相同的缺陷发生在同一项目的不同时间段，或两个相同的缺陷发生在同一项目的不同部分，虽然两个缺陷相同，但它们的缺陷发生的特征不同。为此，针对这些具有不同特征的离散缺陷，依据特征函数提取每个缺陷的特征，并通过特征对比函数遍历所有缺陷，使相同特征的缺陷划分在相同的集合中，每个集合的特征集均不相同，这样的集合称为相似特征缺陷集合(见图2)。

图2 相似特征缺陷集合Fig.2 Similar attributes defect clusters

定义 1 D={d1，d2，…，dn}为 n 个元素的集合，其中 d1，d2，…，dn为缺陷。

定义2 A={a1，a2，a3，…，an}为拥有 n个元素可增减的属性函数集合，其中 a1，a2，…，an为属性函数元素。

定义 3 DF={{d1，d2，…，dk}，{dk+1，dk+2，…，dk+i}，…，{dk+i+1，dk+i+2，…，dn}}为多维可增减集合，其中{d1，d2，…dk}，{dk+1，dk+2，…，dk+i}，…，{dk+i+1，dk+i+2，…，dn}为子集且

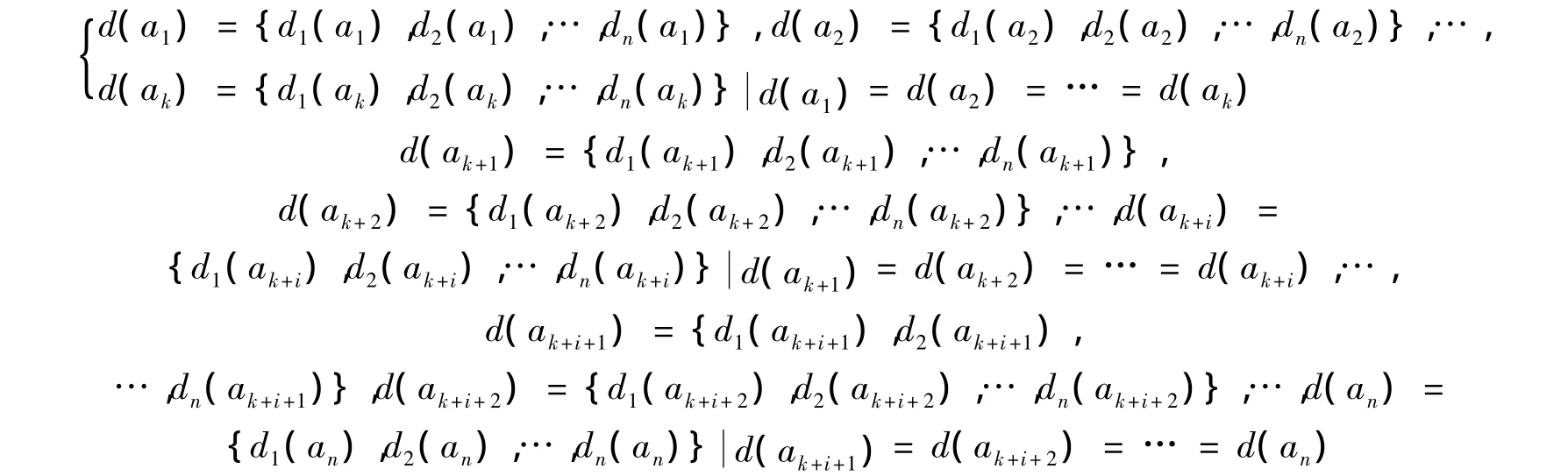
即每个子集中元素的特征相同。

基于相似特征缺陷集合的分组步骤如下。

Algorithm

//输入参数用户数量 n，属性函数集 A={a1，a2，a3，…，an}，i=1。

//输出分组模型。

DF={{d1，d2，…，dk}，{dk+1，dk+2，…，dk+i}，…，{dk+i+1，dk+i+2，…，dn}}

1)创建缺陷集合 D={d1，d2，…，dn};

2)［循环出口］i++，如果i＞n跳出输出DF;

3)Select difrom D;

4)利用属性函数集A计算出ai⇔di的属性集a(di);

5)如果DF={φ}，则建立DF∩{{di}}⇒DF={{di}}和属性总集合dall={{d(ai)}}，否则判断d(ai)所属的属性子集并将其合并到相应的子集中{{…}，{…}∩{di}，…}∩DF⇒DF;

6)转到2)。

3 缺陷关联关系预测方法

依据缺陷间的关联关系，对相似特征缺陷集合进一步聚类。在系统测试、缺陷修复和缺陷预测的过程中，往往会发现一些看似并不存在任何关系的缺陷同时出现在系统中。且出现的时间、频率具有一定的规律性，这些缺陷往往都存在一种隐含关系，也称作关联关系。如果将这些隐含关系的缺陷聚集在一起进行修复，能明显减少缺陷修复时间。在对缺陷的预测过程中，通过对已发现缺陷的分析，可及时预测可能存在与系统有某些关联的缺陷。

关于如何衡量两组缺陷是否具有关联关系，提出了关联系数的概念，关联系数即为两种或多种缺陷同时出现的概率。通过关联系数和相似特征集合间的关系，将相互间强关联关系集合聚集在一起，形成新的关联缺陷聚类，计算方法如下

任取两个DF≡P集合，并将关联关系值最大的两组P集合合并为新的簇，并输出，N为关联关系值，RE为关联关系系数，Pdistance为两组集合间关联关系的逻辑距离。

4 实验仿真结果及分析

在仿真试验中笔者将缺陷分层预测方法与K-means算法进行对比，进一步说明缺陷分层预测方法的高效性和准确性。

实验环境:算法所用的实验环境为Matlab 7.9.2;计算机配置为Windows 7 SP1 32 bit，Intel(R)9800 CPU，8.00 GByte RAM，实验数据为随机产生的数据。

实验数据:随机生成150个缺陷样本。

图3为K-means仿真结果，图4为缺陷分层预测仿真结果。从图3和图4可以看出，K-means的仿真结果缺陷簇的均匀度明显好于分层预测方法，对缺陷预测更加容易。但缺陷预测的最终目的是提升软件质量、加快缺陷修复速率及降低测试成本。过于均匀的缺陷预测结果只能说明缺陷预测的结果并不客观，也不利于系统结构缺陷的集中修复，更不利于人力资源和物力资源的合理分配。对提升软件质量也是低效的。从图4中可以看出，缺陷预测的结果并不均匀，甚至严重失衡，存在有过多的单节点簇。但充分说明了缺陷预测的客观性，测试人员可将大部分精力集中在软件缺陷多发部分，合理分配各种资源，单节点簇及少于3个节点的缺陷簇可作为缺陷预测的干扰点，不参与软件整体缺陷预测，从而达到提升整体软件质量、降低软件成本和软件开发效率的目的。

图4 缺陷分层预测方法Fig.4 Defect hierarchical prediction

图5为两种算法的缺陷簇成簇数量对比图。从图5中可以看出，分层预测方法所成缺陷簇的数量明显多于K-means算法缺陷成簇数量。从而总结出在缺陷数量一定的情况下，分层预测算法的预测精度好于K-means。但如果除去单节点缺陷簇及少于3个节点的缺陷簇，分层预测的缺陷簇数量又少于K-means，而且某些缺陷簇的规模明显大于K-means的成簇规模，从而使缺陷的特点更加显著，更有利于工程项目中整体软件的缺陷修复。

图5 方法对比Fig.5 Method comparison

5 结语

笔者提出了一种系统结构缺陷分层预测方法，该方法通过对缺陷特征的分析，使具有相似特征的缺陷成簇，同时分析簇间的关联关系，使具有强关联关系的缺陷簇再次成簇，最终达到缺陷预测的目的。在仿真实验中，通过对分层预测方法与K-means算法相比较发现:1)缺陷成簇密度的均匀度小于K-means，说明分层预测方法的预测结果更客观，缺陷预测结果的侧重点更突出;2)成簇数量明显多于K-means，除去小于3个节点的节点簇，成簇数量又小于K-means，说明分层预测的缺陷集中出现的特征更加显著。通过以上分析可以得到系统结构缺陷分层预测方法能对软件缺陷进行预测，预测结果好于传统算法K-means。

［1］KHOSHGOFTAAR T M，HERZBERG A，SELIYA N.Resource Oriented Selection of Rule－Based Classification Models:An Empirical Case Study［J］.Software Quality Control，2006，14(4):309－338.

［2］L P L，HERBSLEB J，SHAW M.Forecasting Field Defect Rates Using a Combined Time－Based Approach:A Case Study of OpenBSD ［J］.Proc of the 16th Int'l Symp on Software Reliability Engineering，2005，12(2):193－202.

［3］BASILI V，BRIAND L，WALCELIO L.A Validation of Object Oriented Design Metrics as Quality Indicators［J］.IEEE Trans on Software Engineering，1996，22(10):751－761.

［4］CP Team.Development［EB/OL］. ［2014－12－09］.Version 1.2.2006，2009，http://www.teambcr.com/pr－11415－cp.html.

［5］AKIYAMA F.An Example of Software System Debugging［M］.Miami，USA:Information Processing，1971:111－113.

［6］MAURICE H.Halstead Elements of Software Science:Operating and Programming Systems Series［M］.New York，USA:Elsevier Science Inc，1977:53－56.

［7］LIPOW M.Number of Faults Per Line of Code［J］.IEEE Transactions on Software Engineering，1982，SE－8(4):437－439.

［8］ALBRECHT A J，GAFFNEY J E.Software Function，Source Lines of Code，and Development Effort Prediction:A Software Science Validation ［J］.IEEE Transactions on Software Engineering，1983，SE－9(6):639－648.

［9］TERRY COMPTON B，CAROL WITHROW.Prediction and Control of ADA Software Defects［J］.Journal of Systems and Software，1990，12(3):199－207.

［10］MCCABE T J.A Complexity Measure［J］.IEEE Transactions on Software Engineering，1976，SE－2(4):308－320.

［11］TAGHI M，KHOSHGOFTAAR，NAEEM SELIYA.Fault Prediction Modeling for Software Quality Estimation:Comparing Commonly Used Techniques［J］.Empirical Software Engineering，2008，3(3):255－283.

［12］MUNSON J C，KHOSHGOFTAAR T M.The Detection of Fault－Prone Programs ［J］.IEEE on Transactions Software Engineering，1992，2(4):423－433.

［13］KHOSHGOFTAAR T M，SELIYA N.Improving Usefulness of Software Quality Classification Models Based on Boolean Discriminant Functions［C］∥Proceedings 13th International Symposium on Software Reliability Engineering.New York，USA:ISSRE，2003:221－230.

［14］JAIN A K，DUBES RICHARD C.Algorithms for Clustering Data［J］.Technimetrics，1990，32(2):227－229.

［15］MYERS RAYMOND H.Classical and Modern Regression with Applications［M］.Los Angels，USA:Duxbury/Thompson Learning，1990:223－224.

［16］KHOSHGOFTAAR T M，LANNING D L.A Neural Network Approach for Early Detection of Program Modules Having High Risk in the Maintenance Phase［J］.Journal of Systems and Software，1995，29(1):85－91.

［17］MUNSON J C，KHOSHGOFTAAR T M.Regression Modeling of Software Quality:Empirical Investigation ［J］.Information and Software Technology，1990，32(2):106－114.

［18］KHOSHGOFTAAR T M，MUNSON J C，BHATTACHARYA B B，et al.Predictive Modeling Techniques of Software Quality from Software Measures［J］.IEEE Transactions on Software Engineering，1992，4(2):979－987.

［19］XU L D.Case Based Reasoning［J］.IEEE Transactions on Software Engineering，1994，3(5):10－13.

［20］CHULANI S.Bayesian Analysis Software Cost and Quality Models［D］.Los Angeles:College of Computer，University of Southern California，1999.

［21］CHULANI S.Results of Delphi for the Defect Introduction Model，Sub－Model of the Cost/Quality Model Extension to COCOMOⅡ［R］.Boston，USA:Technical Report，1997:97－504.

［22］CHULANI S，BOEHM B.Modeling Software Defect Introduction and Removal:COQUALMO(Constructive Quality Model)［R］.Philadelphia，USA:Technical Report，1999:99－510.

［23］FAGAN M E.Design and Code Inspections to Reduce Errors in Program Development［J］.IBM System Journal，1976，15(3):182－211.

［24］JONES T C.Measuring Programming Quality and Productivity［J］.IBM Systems Journal，1978，17(1):39－63.

［25］REMUS，ZILLES S.Prediction and Management of Program Quality［C］∥Proceedings of the 4th International Conference on Software Engineering(ICSE'79).Piscataway，NJ，USA:IEEE Press，1979:341－350.

［26］CHILLAREGE R，BHANDARI I，JARIK K，et al.Orthogonal Defect Classification－a Concept for In－Process Measurements［J］.IEEE Trans on Software Engineering，1992，18(11):943－956.

［27］FENTON N E，MARTAIN N，WILLIAM M，et al.Predicting Software Defects in Varying Development Lifecycles Using Bayesian Nets［J］.Information and Software Technology，2007，49(1):32－43.

［28］胡玉鹏，陈治平，林亚平，等.贝叶斯缺陷分析模型及其在软件测试中的应用［J］.计算机应用，2005，25(4):808－810.HU Yupeng，CHEN Zhiping，LIN Yaping，et al.Defect Analysis Model of Bayesian and Its Application in Software Testing［J］.Journal of Computer Applications，2005，25(4):808－810.

［29］马俊伟，王铁军，李庆，等.基于网络信息挖掘的股市影响因素分析［J］.吉林大学学报:信息科学版，2014，32(2):196－200.MA Junwei，WANG Tiejun，LI Qing，et al.Stock Market Influence Factor Analysis Based on Web Data Mining［J］.Journal of Jilin University:Information Science Edition，2014，32(2):196－200.

［30］代宽，赵辉，韩冬，等.基于向量空间模型的中文网页主题特征项抽取［J］.吉林大学学报:信息科学版，2014，32(1):88－94.DAI Kuan，ZHAO Hui，HAN Dong，et al.Theme Feature Extraction of Chinese Webpage Based on Vector Space Model［J］.Journal of Jilin University:Information Science Edition，2014，32(1):88－94.

［31］彭真明，景亮，何艳敏，等.基于多尺度稀疏字典的多聚焦图像超分辨融合［J］.光学精密工程，2014，22(1):169－176.PENG Zhenming，JING Liang，HE Yanmin，et al.Superresolution Fusion of Multiple Sparse Dictionary ［J］.Optics and Precision Engineering，2014，22(1):169－176.

［32］陈恺，陈芳，戴敏，等.基于萤火虫算法的二维熵多阈值快速图像分割［J］.光学精密工程，2014，22(2):517－523.CHEN Kai，CHEN Fang，DAI Min，et al.Fast Image Segmentation with Multilevel Threshold of Two－Dimensional Entropy Based on Fire Fly Algorithm ［J］.Optics and Precision Engineering，2014，22(2):517－523.

［33］XIE M.Software Reliability Modelling［M］.Singapore:Word Scientific Publishing Co Pte Ltd，1991:268－272.

［34］JELINSKI Z，MORANDA P.Software Reliability Research.In:Statistical Computer Performance Evaluation［M］.New York:Academic Press，1972:465－484.

［35］YAMADA S，OHBA M，OSAKI S.S－Shaped Reliability Growth Modeling for Software Error Detection ［J］.IEEE Trans on Reliability，1983，R－32(5):475－478.

［36］YAMADA SHIGERU，OHBA MITSURU，OSAKI SHUNJI.S－Shaped Software Reliability Growth Models and Their Applications［J］.IEEE Transactions on Reliability，1984，R－33(4):289－292.