基于标准差中位数的磁共振信号尖峰去除方法
2015-01-12田宝凤
李 同,林 昊,田宝凤,林 君
(吉林大学a.仪器科学与电气工程学院;b.地球信息探测仪器教育部重点实验室,长春130026)
0 引言
地面核磁共振探测(SNMR:Surface Nuclear Magnetic Resonance)是20世纪80年代发展起来的一种非侵入性地下水资源探测方法。该方法通过产生激发磁场使水中氢质子向高能级跃迁,激发磁场消失后氢质子回归平衡态的过程中将释放能量,通过信号解析出地下环境中的一系列水文地质参数[1]。但是,实际工程应用中阻碍该方法得到大规模推广的主要原因是核磁共振测得的信号很微弱,只有纳伏级,极易受环境噪声中尖峰噪声的干扰。尖峰噪声的幅值往往为有效信号的数倍,混叠在一起会导致信号淹没在其中无法辨识[2-4]。Dalgaard等[5]分析了核磁共振信号中各种噪声的特征以及处理方案,指出数据处理过程中应重视剔除尖峰干扰,否则在后续自适应滤波过程中信号将产生异变,因此,在数据处理过程中应首先对尖峰干扰进行剔除。
针对尖峰噪声的处理一般在探测时设置阈值,当尖峰噪声信号幅值超过阈值时,则舍弃该组测量数据,尽可能保留无干扰数据。然而,当实验环境中有不间断干扰源时需要大量重复实验,因此,有必要进行后期数据处理以解决该类问题。针对此类问题,Jiang等[6]提出了阈值叠加方法,对尖峰较少的数据效果较好,但其实现条件比较苛刻,尖峰越多计算复杂度越高,且只适用于数据处理的后期叠加过程。Strehl[7]提出了运用小波变换的尖峰噪声筛选方案,得到较好的效果,但算法的稳定性较差。为此,笔者针对核磁共振探测应用中的尖峰噪声干扰问题,提出数据处理前期的基于标准差中位数的尖峰筛选方案,经较少次叠加采集后可有效剔除尖峰噪声,以满足核磁共振应用的快速探测需要。
1 核磁共振信号及噪声成分分析
核磁共振地下水探测工作模式如图1所示,地下水中的氢质子经过激发脉冲后在采集系统中形成自由感应衰减信号(FID:Free Induction Decay)[8-10]通常表示为

其中E0为初始振幅;T*2为平均衰减时间常数;ω0表示响应信号的特征频率;φ0为初始相位。
上述参数代表地下水的含水量,孔隙度等信息。其中E0一般为几十到几百纳伏,而混入的噪声干扰往往有几千纳伏,其中包括工频干扰以及尖峰噪声。工频干扰主要来自电力线[11-13],尖峰噪声是由雷电现象或工程机械运转时产生的瞬时电能,在仪器接收回路中产生的激发脉冲,主要特点是突发性,幅度高,随机性强。图2为一组采自农安烧锅镇的混有尖峰噪声的核磁共振信号,可见其中混有两处明显的尖峰,相对微弱的信号被尖峰严重干扰,无法准确显示其衰减形态,影响信号质量。因此,笔者主要针对磁共振探测中的尖峰干扰去除问题进行研究。
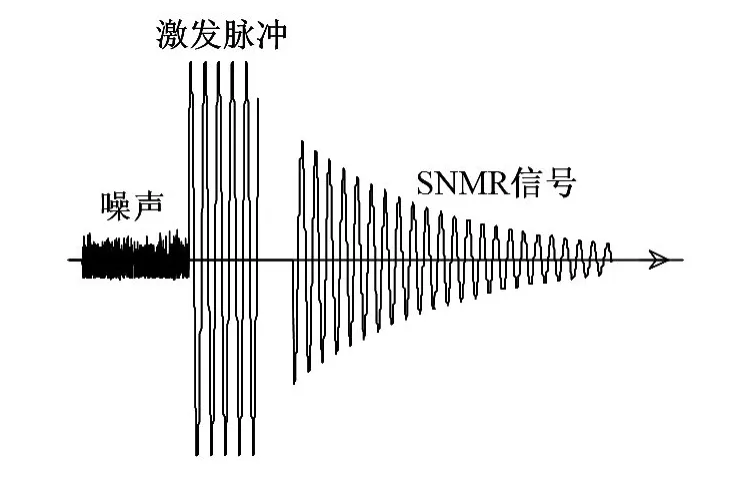
图1 核磁共振信号原理图Fig.1 Surface nuclear magnetic resonance signal

图2 实际采集混有尖峰干扰的信号Fig.2 Signal mixed with peak noise
2 算法原理
以一组相同脉冲矩的N次叠加SNMR信号V(i,t)为例,其中i=1,2,3,…,N。首先通过Hilbert变换提取其包络信号VENV(i,t)[14],再按叠加次数取其平均值得,进行区域极大值判定,筛选信号中的尖峰噪声。

当t=T(n)时,待处理的单次采集信号其中Tthreshold为阈值系数,取值越小,则筛选条件越严苛;σ(t)为VENV(i,t)按采集次数求得的标准差;median{σ(t)}为取中值函数。
通过[V,C]=max{v(T)}找出尖峰噪声的顶峰位置C,可得到尖峰的时域窗口 I,取值范围为其中w为窗口宽度,用来估计尖峰噪声的时域范围。最后将锁定的尖峰噪声数据替换为叠加信号的均值

3 仿真信号的处理
结合一般SNMR野外实验工作方法以及噪声特点进行仿真实验。依据式(1)生成一组32次采集的纯净SNMR信号,其中单次采集信号如图3所示。在此基础上对每组数据同时混进随机噪声及尖峰噪声。图4为32次叠加数据中的第7组数据,该组信号共混有3处尖峰干扰,分别位于0.8 ms,110.3 ms和237.7 ms处,干扰幅值很大,位置无规律。

图3 模拟的纯净核磁共振信号Fig.3 Synthetic signal

图4 模拟的混有尖峰干扰的信号Fig.4 Synthetic signal mixed with peak noise
为消除尖峰噪声的干扰,采用上述方法对数据集进行处理,通过式(2)对多次采集的数据集中各时刻的比对筛选尖峰噪声,其过程如图5所示。图5中黑色方块分别表示图4中3处尖峰时刻在各采集次数下的信号幅值,虚线的取值为式(2)不等式右侧部分,代表筛选尖峰噪声的下限参考值,所有大于该值的数据点被认定为尖峰干扰,由此找出其时域坐标,进而将其剔除,阈值Tthreshold的取值会影响识别尖峰干扰的准确性。Tian等[15]讨论了标准差系数与信噪比的适应关系,认为该系数设定取决于环境噪声幅度。当环境噪声较弱时,信噪比高,调整较低的阈值系数便可筛选尖峰干扰;当环境噪声较强时,信噪比较低,此时阈值系数若不进行调整,会将有效的核磁共振信号误认为尖峰干扰。因此,处理低信噪比数据时应适当增大阈值,根据噪声水平,这里阈值系数取值5,可见在此阈值条件下能准确地筛选各处尖峰干扰。

图5 多次采集下阈值为5时的尖峰干扰筛选效果Fig.5 Recognizing peak noise when threshold is 5
该组数据经过尖峰噪声剔除的波形如图6所示,图7a,图7b分别为该组数据处理前后的包络信号。对比图5可以看出,该组信号受到3组脉冲干扰明显,幅值达到相应时刻平均值的10倍。合理的阈值设定可以准确地定位尖峰干扰,将其筛除,并很好地保留了其余信号,可明显看出尖峰剔除后信号的衰减形态。
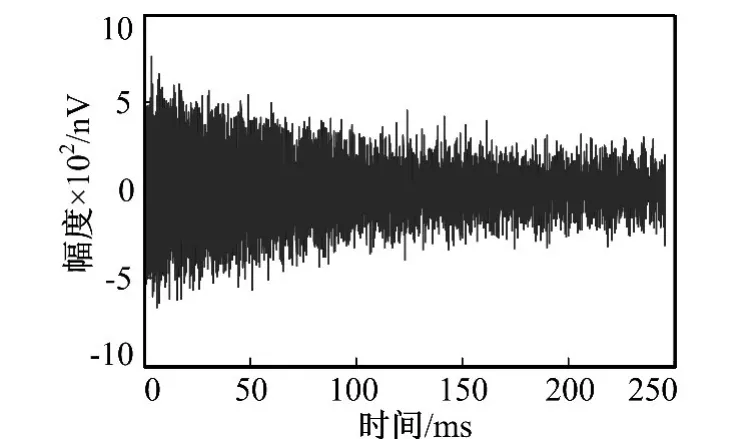
图6 尖峰剔除后的仿真信号Fig.6 Signal after deleting peak noise
4 野外实测数据的处理
上述仿真实验证实了尖峰剔除方法的有效性,可将该方法应用于实际采集核磁共振信号的处理过程中。图2是采集于农安县烧锅镇的核磁共振探测信号,共进行32次叠加采集,图示为尖峰干扰较明显的第6次叠加数据,图8、图9给出了该组信号经过尖峰剔除后的结果,原数据中存在两处明显尖峰,分别在19.92 ms以及75.92 ms处。由图9可看出,经过计算处理,两处尖峰干扰均被剔除。
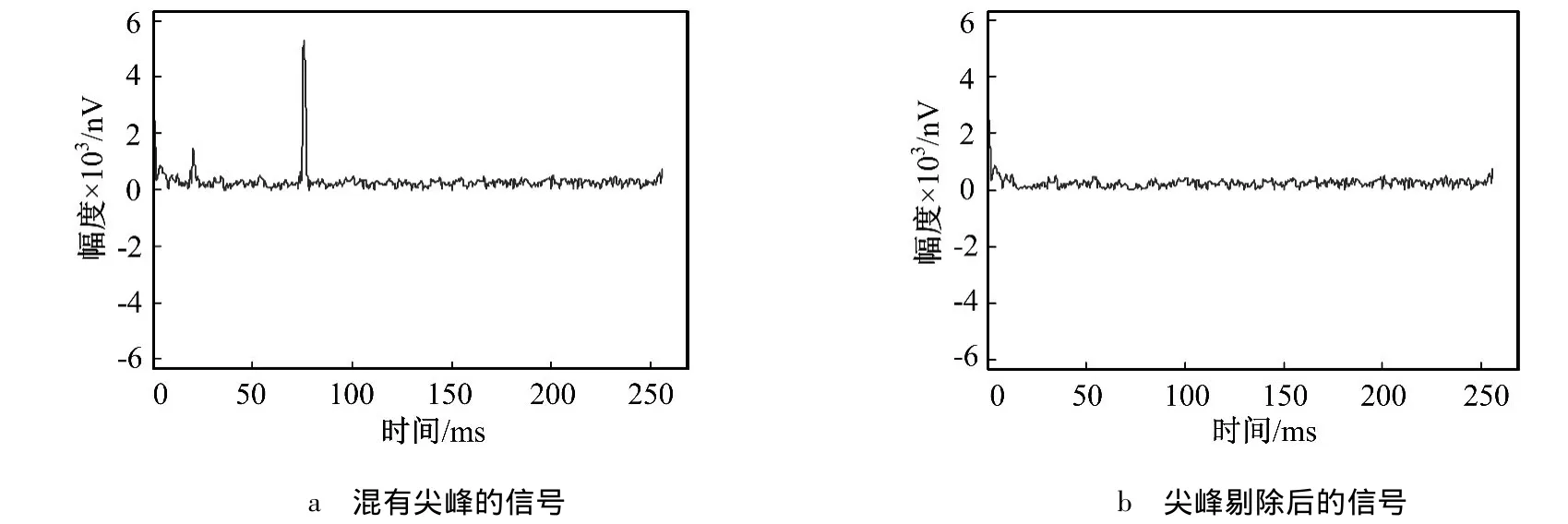
图9 尖峰剔除前后的实测信号包络曲线对比Fig.9 Envelope of field signal before and after filtering
通过包络数据可以看出,尖峰干扰破坏了信号的连续衰减形态,经过计算处理后尖峰干扰可被有效滤除,证明了该算法可以解决实际采集信号中的尖峰干扰问题,有较好的实用性。
5 结语
由于尖峰干扰的存在,增大了后续数据处理的计算难度,而传统的尖峰噪声滤波方案在逐渐发展的核磁共振应用环境中受到局限。笔者设计了基于重复采集数据的标准差中位数滤波方案,针对核磁共振信号中尖峰干扰进行筛选剔除。该方案具有计算简单、准确度高等优势。通过对仿真核磁共振信号的处理可以看出,该算法可准确剔除混在信号中的3处尖峰干扰,同时保留真实信号,尤其信号初段的尖峰幅值在真实信号的10倍以上,对其有效滤除后还原了真实信号的衰减形态,对实际采集的核磁共振信号的处理也得到了同样的效果,从而验证了该方法的有效性。
[1]林君.现代科学仪器及其发展趋势[J].吉林大学学报:信息科学版,2002,20(1):1-7.LIN Jun.Developing Trend of Modern Scientific Instrument[J].Journal of Jilin University:Information Science Edition,2002,20(1):1-7.
[2]YARAMANCI U.New Technologies in Groundwater Exploration Surface Nuclear Magnetic Resonance[J].Geologica Acta:An International Earth Science Journal,2004,2(2):109-120.
[3]JUAN PLATA,FELIX RUBIO.MRS Experiments in a Noisy Area of a Detrital Aquifer in the South of Spain[J].Journal of Applied Geophysics,2002,50(1/2):83-94.
[4]UGUR YARAMANCI,GERHARD LANGE,MARIAN HERTRICH.Aquifer Characterisation Using Surface NMR Jointly with other Geophysical Techniques at the Nauen/Berlin Test Site[J].Journal of Applied Geophysics,2002,50(1/2):47-65.
[5]DALGAARD E,AUKEN E,LARSEN J J.Adaptive Noise Cancelling of Multichannel Magnetic Resonance Sounding Signals[J].Geophysical Journal International,2012,191(1):88-100.
[6]JIANG Chuandong,LIN Jun,DUAN Qingming,et al.Statistical Stacking and Adaptive Notch Filter to Remove High-Level Electromagnetic Noise from MRS Measurements[J].Near Surface Geophysics,2011,9(5):459-468.
[7]STREHL S.Development of Strategies for Improved Filtering and Fitting of Snmr Signals[D].Berlin:Institute of Applied Geosience,Berlin University of Technology,2006:57-64.
[8]林君,段清明,王应吉,等.核磁共振找水仪原理与应用[M].北京:科学出版社,2011:2-3.LIN Jun,DUAN Qingming,WANG Yingji,et al.Theory and Design of Magnetic Resonance Sounding Instrument for Groundwater Detection and Its Applications[M].Beijing:Science Press,2011:2-3.
[9]翁爱华,王雪秋,刘国兴,等.导电性影响的地面核磁共振反演[J].地球物理学报,2007,50(3):890-896.WENG Aihua,WANG Xueqiu,LIU Guoxing,et al.Nonlinear Inversion of Surface Nuclear Magnetic Resonance over Electrically Conductive Medium[J].Chinese Journal of Geophysics(in Chinese),2007,50(3):890-896.
[10]潘玉玲,张昌达.地面核磁共振找水理论和方法[M].武汉:中国地质大学出版社,2000:37.PAN Yuling,ZHANG Changda.The Theory and Method of SNMR [M].Wuhan:China University of Geosciences Press,2000:37.
[11]林婷婷,慧芳,蒋川东,等.分层多指数磁共振弛豫信号反演方法研究 [J].地球物理学报,2013,56(8):2849-2861.LIN Tingting,HUI Fang,JIANG Chuandong,et al.Layered Multi-Exponential Inversion Method on Surface Magnetic Resonance Sounding Dataset[J].Chinese Journal Geophysics,2013,56(8):2849-2861.
[12]易晓峰,李鹏飞,林君,等.基于多匝环形线圈的核磁共振信号响应计算与试验研究[J].地球物理学报,2013,56(7):2484-2493.YI Xiaofeng,LI Pengfei,LIN Jun,et al.Simulation and Experimental Research of MRS Response Based on Multi-Turn Loop[J].Chinese Journal Geophysics,2013,56(7):2484-2493.
[13]田宝凤,段清明.核磁共振信号工频谐波的自适应滤波方法 [J].吉林大学学报:信息科学版,2009,27(3):223-228.TIAN Baofeng,DUAN Qingming.Removal Method of Industrial Frequency Harmonics in Nuclear Magnetic Resonance Signal Based on Adaptive Filter[J].Journal of Jilin University:Information Science Edition,2009,27(3):223-228.
[14]张旻,程家兴,樊甫华,等.利用 Hilbert变换提取信号瞬时特征参数的问题研究[J].电讯技术,2003,43(4):44-48.ZHANG Min,CHENG Jiaxing,FAN Fuhua,et al.Study on the Problems in ExtractingInstantaneous Characters of Signals Based on Hilbert Transform [J].Telecommunication Engineering,2003,43(4):44-48.
[15]TIAN Baofeng,ZI Yanyong,ZHOU Yuanyuan,et al.Research on Pulse Noise Elimination Algorithm of Magnetic Resonance Sounding Full-Wave Signal [C]∥ 10th International Computer Conference on Wavelet Active Media Technology and Information Processing.Chengdu,China:IEEE,2013,6-10.
