基于布谷鸟搜索算法的最大似然DOA估计

张义元，张志成，石要武，刘昱兵

(吉林大学通信工程学院，长春130012)

0 引言

阵列信号处理是信号处理重点研究方向之一，近些年来得到迅速发展。信号的波达方向(DOA:Direction of Arrival)估计是阵列信号处理的重要研究内容和持续研究热点之一，在雷达、声纳、通信和地震学等领域应用前景很大。最大似然(ML:Maximum Likelihood)参数估计方法是参数估计理论的典型估计方法，Ziskind首先将最大似然参数估计应用于信号的 DOA估计［1，2］。与 MUSIC(Multiple Single Classification)算法和ESPRIT(Estimating Single Parameters via Rotational Invariance Techniques)算法相比，ML算法的估计性能良好，具有很好的稳定性，尤其是低信噪比情况下，ML算法比MUSIC及其他子空间分解类算法性能强很多。但由于最大似然DOA估计的似然函数是多维非线性的极值问题，需要全局极值的多维搜索，运算量非常大。

20世纪后期，仿生智能算法脱颖而出，如粒子群优化算法(PSO:Particle Swarm Optimization)、遗传算法(GA:Genetic Algorithm)和人工蜂群算法(ABC:Artificial Bee Colony)等，它们通过模拟自然界中生物的行为解决大规模复杂优化问题［3，4］。针对最大似然DOA估计问题的复杂性，一些研究学者将仿生智能算法应用于信号的DOA估计，取得了一些效果。Li等［5］将GA算法应用于最大似然DOA估计，首次实现了仿生算法的最大似然DOA估计。但GA算法容易出现过早收敛等问题。李俊武等［6］利用PSO算法做最大似然DOA估计，性能良好，但由于PSO算法收敛速度较慢，容易陷入局部最优解，在求解多个方向角同时估计时仍存在不足。

布谷鸟搜索算法(CS:Cuckoo Search)是YANG等［7］提出的仿生智能算法。该算法主要基于布谷鸟寄生繁殖机理和莱维飞行搜索两方面。基于CS算法方法简捷，求解复杂问题时优化速度快。笔者将改进后的CS算法应用于最大似然算法DOA估计，解决最大似然DOA估计存在的计算量大，容易陷入局部最优等问题，对于多个方向角的联合估计，力图获得较好的估计精度和收敛性能。

1 信号的DOA估计

1.1 阵列信号模型

假设均匀线阵信号模型的阵元是均匀且各向同性的，阵元数为M，相邻阵元间距为d，有P个窄带远场信号源以平面波入射，入射角度为θk，入射波长为λ［8］，则阵元接收数据可写成矢量形式

其中 X(t)=［x1(t)，x2(t)，…，xM(t)］T为 M 维的接收数据矢量;S(t)=［s1(t)，s2(t)，…，sP(t)］T为 P维的信号源矢量;N(t)=［n1(t)，n2(t)，…，nM(t)］T为M维的噪声矢量，并假定噪声为高斯白噪声，在空间和时间上均独立;A=［a(θ1)，a(θ2)，…，a(θP)］为M×P维的阵列导向矩阵，其第k列a(θk)为第 k个信号源 sk的导向矢量为a(θk)=［1，exp(jφ(θk))，…，exp(j(M －1)φ(θk))］T，φ(θk)=为第k个信号源矢量与阵列法向量的夹角。

通过以上阵列信号DOA估计的数学模型，可以得到阵列接收数据的协方差矩阵

其中RS为信号的协方差矩阵，RN为噪声的协方差矩阵。

1.2 最大似然算法测向原理

假设噪声为平稳、空间和时间均不相关的高斯随机过程，均值为零，方差为σ2;源信号为未知的确定性信号，则有

由概率论的理论［9］，几个独立且同分布高斯随机过程的概率密度函数

对式(5)取对数，有

整理可得，最大似然算法的DOA估计谱函数

经数学推导后可得代价函数

目标函数式(8)是关于入射方向角θ1，θ2，…，θP的多维非线性函数，直接求解最优值，运算量非常大，且由于其通常具有复杂的局部极值结构，很难保证收敛到全局最优解;另一方面，求其导数较难。因此，按照传统的优化算法通过目标函数值及其目标函数导数值求解，难以解决全局极值问题。

2 最大似然DOA估计的函数优化

2.1 布谷鸟搜索算法

布谷鸟搜索算法是随机全局优化算法，其灵感来源于布谷鸟将它育雏一些小布谷鸟的任务寄生在其他鸟类的巢中的现象。在自然界中，布谷鸟是通过随机的或是类似随机的方式寻找适合自己产蛋的鸟窝位置，为了能更好模拟布谷鸟寻窝的方式，首先需要设定以下3个理想的状态:

1)一只布谷鸟每次只产一个蛋，并随机将这个蛋放到某个鸟窝中;

2)最佳鸟窝中高性能的蛋将会被保留到下一代;

3)鸟窝的数量是固定的，蛋放到鸟窝中被宿主发现的概率为Pa∈［0，1］。

在被宿主发现时，宿主鸟可选择抛出异样鸟蛋，或直接放弃该鸟巢，重新建造一个新的鸟巢［10］。

在CS搜索算法中，1个鸟巢表示1个候选解。布谷鸟搜索算法采用莱维随机行走方式更新鸟窝位置

其中Xg，t表示第g代第t个解;α＞0表示步长的大小，用于控制随机搜索的范围。⊕是点乘积，L(β)服从Levy概率分布

基于上述假设，布谷鸟搜索算法的主要步骤描述如下:

Step1 选取目标函数f(X)，X=(x1，…，xd)T，随机产生一组鸟窝的初始位置Xi(i=1，2，…，n)，并设置算法参数;

Step2 计算每个鸟窝的目标函数值，并记录当前的最好解;

Step3 保留上一代中最好的鸟窝位置，对其他的鸟窝位置按式(9)进行更新;

Step4 将新得到一组鸟窝位置与上一代进行对比，若较好，则将该组最优解作为当前的最优位置;

Step5 用服从均匀分布的随机数R∈［0，1］作为鸟窝宿主发现外来鸟蛋的可能性与Pa比较，若R＞Pa，则随机改变鸟窝位置，得到一组新位置;

Step6 若未满足结束条件，则返回Step2;

Step7 输出全局最优位置。

2.2 基于布谷鸟搜索算法的最大似然DOA估计

将布谷鸟搜索算法应用于空间信号的DOA估计问题。最大似然算法的谱函数P(θ)作为待搜索的目标函数，每组鸟窝位置Xi(i=1，2，…，n)代表待估计方向角在第t次迭代中的n个解θi(t)(i=1，2，…，n)。经过每次迭代，按照式(9)得到一组新解θi(t+1)，并对基本的布谷鸟搜索算法作如下改进。

1)将初始化过程产生N个标准正态分布的初始化种群，改为服从(－π/2，π/2)的均匀分布的N个初始化种群。

2)对式(9)更改步长控制方式，具体处理如下。

①为能从当前最优解中获得更多有用的步长信息［11］，计算步长

并加入惯性权重α0=0.1(1－k/M)，其中M为最大迭代次数，k为当前的迭代次数，Xbest表示当前最优解。

②为了便于计算，采用式(12)计算Levy随机数

其中u，v服从标准正态分布，β=1.5。

生成新的解。

如被宿主发现，在按一定的概率(发现概率Pa)丢弃部分解之后，算法采用偏好随机游动重新生成相同数量的解

其中r为缩放因子，为服从(0，1)均匀分布的随机数;Xg，t和Xg，k表示g代的两个随机解。

因此，按照布谷鸟搜索算法的程序和式(9)进行算法的迭代，经过一定次数的迭代，可得到相应性能良好的解，作为最大似然算法DOA估计的方向角。

显然，综合式(11)～式(13)，在Levy飞行中，CS搜索算法采用下面等效的位置更新公式

3 实验与结果

在Matlab仿真实验平台上，选用其他几种较受欢迎的元启发式仿生智能算法，包括微分进化算法(DE:Differential Evolution)，粒子群优化算法(PSO:Particle Swarm Optimization)和克隆选择算法(CLONALG:Clonal Genetic)，分别做最大似然DOA估计，比较布谷鸟搜索算法与上述仿生智能算法的收敛性及其精度。

实验1 收敛实验。阵列模型选用均匀线阵，阵元数为10。阵元之间的间距设为信号载波波长的一半，快拍数为100，噪声为0的高斯白噪声。搜索线阵范围为(－90°，90°);4种仿生优化算法的参数设置如表1所示。其中Q为种群数量，I为最大迭代次数，F为变异因子，c为交叉概率，c1为加速因子1，c2为加速因子2，m为变异概率，r为抗体个数，p为发现概率，a为搜索步长。图1是入射角为(20°，50°)时最优目标函数值随迭代次数的变化情况，图2是入射角为(20°，50°，－10°)时最优目标函数值随迭代次数的变化情况。从图1可以看出，有两个入射信号时，布谷鸟搜索算法较其他的仿生优化算法具有较快的收敛特性;而图2中，在同时有3个入射信号时，布谷鸟搜索算法的收敛特性也较好，搜索到的似然函数值更接近于全局最优解，所以在入射信号数目增多、待优化目标函数复杂的情况下，布谷鸟搜索算法的收敛速度和全局优化能力较为突出。

表1 不同优化算法的参数设置Tab.1 Parameter settings of different algorithm

图1 两个入射信号时布谷鸟搜索算法和其他算法的收敛性比较Fig.1 Comparison of the convergence for cuckoo search algorithm and other algorithms when the two incident signals

图2 3个入射信号时布谷鸟搜索算法和其他算法的收敛性比较Fig.2 Comparison of the convergence for cuckoo search algorithm and other algorithms when the three incident signals

实验2 算法的精度实验。所有条件均与实验1相同，用均方根误差

作为衡量算法精度的标准。其中N为信号源的个数，NMC为实验次数，θi表示第i个信源的真实到达角，^θi(k)为第k次估计的到达角的估计值。实验选取信噪比的变化范围在－15～15 dB之间，在高斯白噪声背景下，采用100次独立Monte Carlo实验，得到均方根误差随信噪比的变化曲线比较如图3所示。从图3可以看出，几种优化算法在低信噪比时误差较为接近，而随着信噪比的增加，布谷鸟搜索算法优化的DOA谱估计的估计误差较低，估计的稳定性较好。

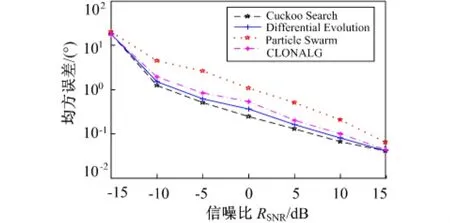
图3 与其他优化算法比较的DOA估计均方根误差Fig.3 RMSE of DOA estimation compared with other optimization methods

4 算法的计算量分析

最大似然DOA估计算法需要通过谱峰搜索实现参数估计，计算量主要由信号参数的维数和搜索步长决定。以估计两个入射角为例，计算量为 O((θmax1－θmin1)(θmax2－ θmin2)/Δθ1Δθ2)，其中(θmin，θmax)和 Δθ分别为DOA的搜索范围和搜索步长。而基于布谷鸟搜索算法的最大似然DOA估计中谱峰搜索的计算量主要由种群数量和迭代次数决定，可表示为O(NIN+N)。其中N和IN分别为种群数量和迭代次数。

取DOA搜索范围为(－90°，90°)，传统网格搜索方法和笔者方法的计算量比较如表2所示。传统网格搜索方法的步长Δθ=0.1;笔者方法种群数量为100，迭代次数为100。从表2中可以清楚地看到，在最大似然DOA估计中，同传统的网格搜索方法相比，布谷鸟搜索算法可大幅度减少DOA估计的计算量。

表2 算法的计算量比较Tab.2 Conparison of calculation amount

5 结 语

笔者将最大似然DOA谱估计和布谷鸟搜索算法相结合，提出了基于布谷鸟搜索算法的最大似然DOA估计方法。该方法在保留最大似然DOA估计良好性能的同时，加入了改进的布谷鸟搜索策略，实现了对最大似然谱函数的优化搜索，大幅度降低了DOA估计的计算量。仿真实验表明，在相同的实验条件下，与其他方法相比，该算法具有搜索精度高、优化速度快、全局搜索能力强等特点。而在待估计信号源个数增多，最大似然DOA谱函数更加复杂的情况下，基于CS优化的最大似然DOA估计也能实现较快、较好的估计。所以笔者提出的改进CS优化策略，是解决此类复杂DOA谱峰搜索问题的有效方法。

［1］LEE J Y.Acoustic DOA Estimation:An Approximate Maximum Likelihood Approach ［J］.IEEE Systems Journal，2013，8(7):131－141.

［2］王永德，陈旗.基于最大似然估计的空间谱测向技术［J］.计算机与数字工程，2010，38(9):123－127.WANG Yongde，CHEN Qi.Direction Finding of Spatial Spectrum Based on Maximum Likelihood Estimation［J］.Computer＆Digital Engineering，2010，38(9):123－127.

［3］CIVICIOGLU P.A Conception Comparison of the Cuckoo Search，Particle Swarm Optimization Differential Evolution and Artificial Bee Colonial Gorithms［J］.Artificial Intelligence Review，2011，39(4):315－346.

［4］YANG X S，DEB S.Multi－Objective Cuckoo Search for Design Optimization［J］.Computers ＆ Operations Research，2013，40(6):1616－1624.

［5］LI M，LU Y.Genetic Algorithm Based Maximum Likelihood DOA Estimation［C］∥Proceedings of Radar Conference 2002.Edinburgh，UK:［s.n.］，2002，10:502－506.

［6］李俊武，俞志富.改进粒子群算法在DOA估计中的应用［J］.计算机工程与应用，2013，49(9):203－206.LI Junwu，YU Zhifu.Improved PSO and Its Application to DOA Estimation ［J］.Computer Engineering and Applications，2013，49(9):203－206.

［7］YANG X S，DEB S.Cuckoo Search via Lévy Flights［C］∥Proc of the World Congress on Nature and Biologically Inspired Computing.Piscataway:IEEE Publications，2009:210－214.

［8］ZHANG Zhicheng，SHI Yaowu.Application of Artificial Bee Colony Algorithm to Maximum Likelihood DOA Estimation［J］.Journal of Bionic Engineering，2013，10(1):100－109.

［9］WANG H，KAY S.Maximum Likelihood Angle－Doppler Estimator Using Importance Sampling ［J］.IEEE Transactions on Aerospace and Electronic Systems，2010，46(2):610－622.

［10］李煜，马良.新型元启发式布谷鸟搜索算法［J］.系统工程，2012，30(8):64－69.LI Yu，MA Liang.The New Meta－Heuristic Cuckoo Search Algorithm ［J］.Systems Engineering，2012，30(8):64－69.

［11］王李进，尹义龙.逐维改进的布谷鸟搜索算法［J］.软件学报，2013，24(11):2687－2698.WANG Lijin，YIN Yilong.Cuckoo Search Algorithm with Dimension by Dimension Improvement［J］.Journal of Software，2013，24(11):2687－2698.