基于信噪杂比最大能量分配认知雷达波形设计

鞠默然，李新波，石要武

(吉林大学通信工程学院，长春130022)

0 引言

认知雷达是一种新兴的智能雷达，也是未来雷达发展的主要趋势［1－5］。其特点主要是引入了雷达的闭环系统:认知雷达通过先验信息设计首次发射的波形，波形经过环境反射，携带着环境信息被雷达接收机接收;从回波中提取环境信息和目标信息作为下一次发射波形的先验信息，设计下一次的发射波形，以提高雷达系统对目标的识别效率。

目前，认知雷达最优波形设计主要有两种方法:一种是基于最大互信息的波形设计方法［6－9］，该方法针对目标的最优估计，通过最优波形将能量尽可能多地分配在目标响应强的频域内，以获得最大化的回波与目标间的互信息，较好地解决了杂波和噪声背景下的波形优化问题，通过最大化目标回波与不同目标特性差别之间的互信息提高目标的可分性，获得较好的识别效果;另一种方法是基于点目标的最大SINR(Signal to Interference plus Noise Ratio)的波形设计方法［10，11］，该方法通过最大化SINR，获取最优波形，以提高雷达对目标的检测性能，文献［11］给出的方法是将目标假设为点目标，没有对扩展目标进行分析和讨论。以上两种方法都利用了拉格朗日乘子法，需要对乘子进行搜索，计算量大。

笔者针对认知雷达波形设计，推导出在非点目标背景下基于SINR拉格朗日乘子法的最优波形设计公式，提出了基于SINR最大能量分配的波形设计方法。该方法提高了计算效率，减少了计算量，具有更好的通用性。

1 基于SINR拉格朗日乘子法的最优波形设计

SINR是反映雷达检测性能的一个重要参数。最大化SINR的波形设计算法是认知雷达信号处理中波形设计的重要方法之一［11］。

通常，SINR谱密度公式表示为［11］

其中Pg(f)为假设目标的脉冲响应的功率谱密度，Pn(f)为高斯白噪声的功率谱密度，Pc(f)为杂波的功率谱密度，X(f)为最优发射波形。

在带宽为w的情况下，SINR表示为

发射能量表示为

将式(2)作为需要优化的目标函数，式(3)作为发射能量的约束条件，利用拉格朗日乘子法，获取SINR的最优解

当所有蚂蚁完成一次循环后，为使搜索过程更具指导性，让蚂蚁的领域集中在当前循环为止的最好路径领域内，需对全局最优及全局最差路径的信息素轨迹量进行更新。

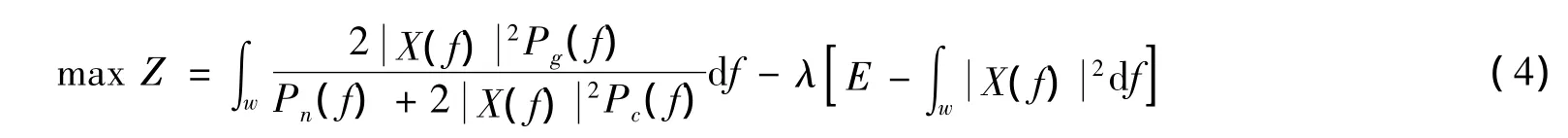
若使式(4)中的目标函数最大，可等效为使式(4)中的积分式最大，用U表示积分式，即

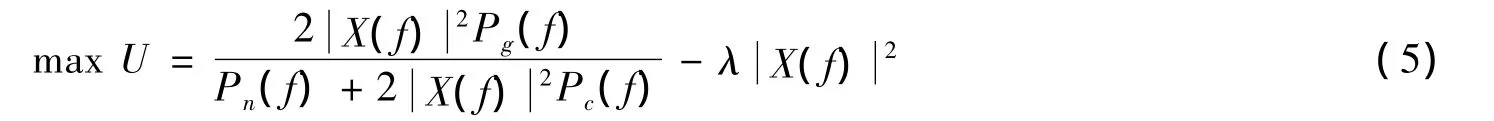
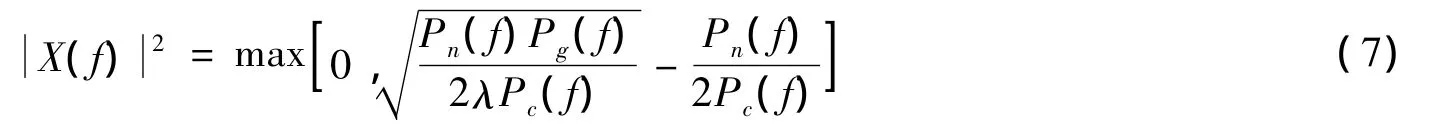
其中λ由发射波形的能量决定，由

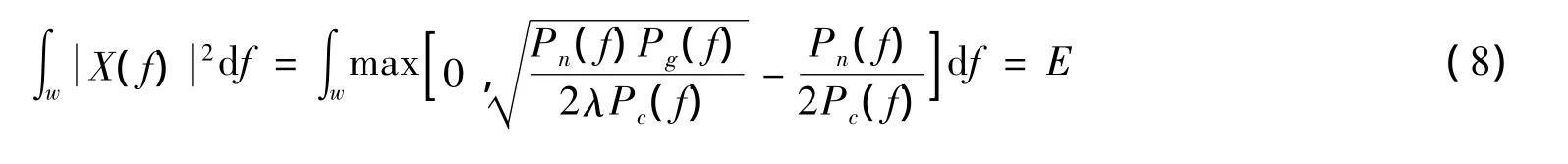
解得。

2 基于能量分配的最大SINR波形设计

2.1 算法的基本思想

算法首先将SINR离散化。离散化的SINR为

其中fk=kΔ f，并且Δ f=w/N。

然后将能量约束E离散化。离散后的能量为

将离散的能量简化替代，得

则式(9)写成

所以求取最优发射波形的优化问题可转化为能量约束问题。

设

对emax进行离散化，将其分成M份，每份能量为Δ，称其为最小能量分配单元，emax=MΔ。所以对每个频段的 e(k)都可以在集合{0，Δ，2Δ，3Δ，…，MΔ}中取值。

在能量分配算法中，每次分配Δ单位的能量，直到所有能量都分配完。在每次分配能量时，对于所有k，选取Z(e(k)，k)中最大的 Z(e(kmax)，kmax)，为 e(kmax)分配 Δ能量，并且将 Z(e(kmax)，kmax)由Z(2Δ，kmax)－Z(Δ，kmax)替换，即说明能量分配从Δ到2Δ。然后重复以上步骤，直到所有的能量都被分配完，最终得到的e(k)即为所求的最优发射波形能量谱。

2.2 算法的步骤与流程

第k个频段内分配jΔ能量时所对应的SINR用矩阵A中的元素A(k，j)表示为

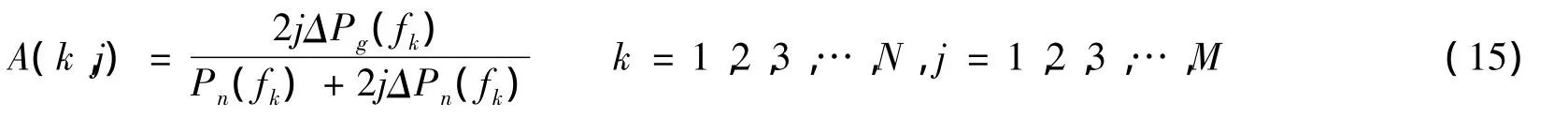
算法的具体步骤如下:

1)求取矩阵A，并初始化能量矩阵e，e(k)=0，k=1，2，…，N;

2)找出 A(k，1)(k=1，2，…，N)中最大的 A(d，1)，并为能量矩阵赋值 e(d)=Δ;

3)更新矩阵 A，令 t=A(d，1)，对于所有的 j，j=1，2，3，…，M，令 A(d，j)=A(d，j+1)－t;

4)若j＜M，则跳转至2)，直到j=M，即将所有的能量分配完。

3 算例的仿真实验

设定M=1 000，采样点数为512，信号频率为f=［0，1］，总能量为1，噪声的功率谱密度为1。

实验1 图1为已知的目标谱和杂波谱，图2和图3分别为基于能量分配的SINR最优波形和基于拉格朗日乘子法的SINR最优波形。

图1 目标谱方差和杂波谱方差Fig.1 The target spectrum variance and clutter spectrum variance

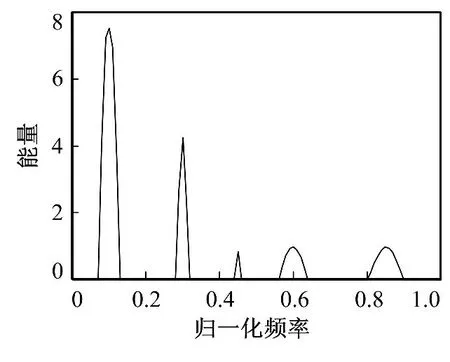
图2 基于能量分配的SINR最优波形Fig.2 The SINR optimal waveform based on energy distribution

图3 基于乘子法的SINR最优波形Fig.3 The SINR optimal waveform based on Lagrange multiplier method

从实验1可以看到，两种算法获得的最优波形相近。为得到最大的SINR，最优波形尽可能地把能量分配给杂波响应较弱、目标响应较强的频段。

图4 目标谱方差和杂波谱方差Fig.4 The target spectrum variance and clutter spectrum variance

图5 基于能量分配的SINR最优波形Fig.5 The SINR optimal waveform based on energy distribution

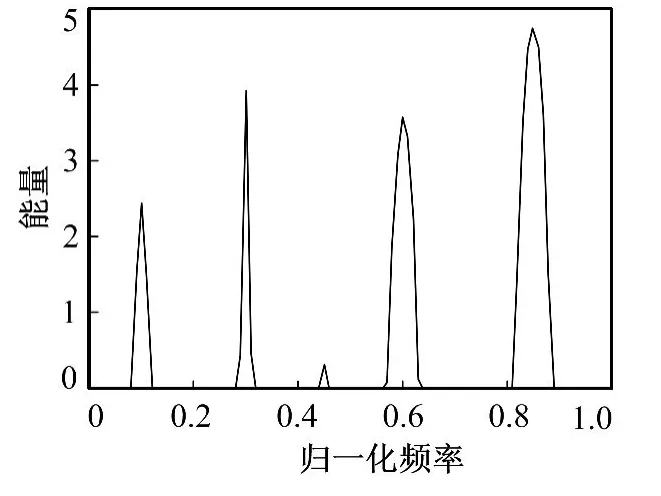
图6 基于乘子法的SINR最优波形Fig.6 The SINR optimal waveform based on Lagrange multiplier method

实验2 在与实验1相同条件下，改变杂波谱的分布。图4为变化的目标谱和杂波谱，图5和图6分别为基于能量分配的SINR最优波形和基于拉格朗日乘子法的SINR最优波形。从实验2可以看出，当杂波谱发生响应的频移时，两种算法所获得的最优波形仍然相近。为了得到最大的SINR，最优波形尽可能地把能量分配给杂波响应较弱、目标响应较强的频段。

实验1和实验2分别给出了基于能量分配算法和拉格朗日乘子算法的SINR最优波形。从两个实验结果可以看出，两种算法的最优波形的能量谱是相近的。当杂波的功率谱密度在某些频段上较小或为0时，发射波形将在该频段上分配更多的能量;反之，在杂波很强或目标相对较弱的频段上，发射波形的能量谱在该频段上将分配较少的能量。但从总体上看，最优波形的能量谱与目标谱的变化趋势是一致的。为了补偿杂波，最优发射波形的幅度与目标谱相比有了变化，以保证通过最优波形对能量的合理分配获取最大化的SINR。

4 结语

对于拉格朗日乘子法的SINR认知雷达最优波形设计，由于需要引入拉格朗日乘子，在求取最优波形时，需要对乘子进行搜索，计算量大且繁琐。与拉格朗日乘子法相比，笔者提出的最大能量分配SINR认知雷达最优波形设计方法，通过对能量的合理分配设计最优波形，获取最大化的SINR，避免了初始值对最优波形的影响。该方法具有计算量小、通用性广泛等优点。

［1］GUERCI J R.Cognitive Radar:A Knowledge－Aided Fully Adaptive Approach［C］∥Proceedings of IEEE Radar Conference.Washington DC:IEEE Press，2010:1365－1370.

［2］AYKIN S.Cognitive Radar:A Way of the Future［J］.IEEE Signal Processing Magazine，2006，23(1):30－40.

［3］HAYKIN S.Cognitive Dynamic Systems［J］.IEEE Signal Processing，2007，4(1):1369－1372.

［4］GUERCI J R.Cognitive Radar:The Knowledge－Aided Fully Adaptive Approach［M］.Boston/London:Artech House，2010.

［5］XUE Yanbo.Cognitive Radar:Theory and Simulations［D］.Canada:College of Computer Engineering，Mcmaster University，2010.

［6］纠博，刘宏伟，李丽亚，等.雷达波形优化的特征互信息方法［J］.西安电子科技大学学报，2009，36(1):139－144.JIU Bo，LIU Hongwei，LI Liya，et al.Feature Mutual Information Method for Radar Waveform Optimization ［J］.Journal of Xidian University，2009，36(1):139－144.

［7］纠博，刘宏伟，李丽亚，等.一种基于互信息的波形优化设计方法［J］.西安电子科技大学学报，2008，35(4):678－684.JIU Bo，LIU Hongwei，LI Liya，et al.Method for Waveform Design Based on Mutual Information ［J］.Journal of Xidian University，2008，35(4):678－684.

［8］BELL M R.Information Theory and Radar Waveform Design ［J］.IEEE Trans on Information Theory，1993，39(5):1578－1597.

［9］GUO D，SHAMAI S，VERDU S.Mutual Information and Minimum Mean－Square Error in Gaussian Channels［J］.IEEE Transactions on Information Theory，2005，51(4):1261－1282.

［10］胡旭，贾鑫.一种新的认知雷达波形优化方法［J］.电子信息对抗技术，2014，29(1):33－37.HU Xu，JIA Xin.A New Method of Cognitive Radar Waveform Optimization［J］.Electronic Information Warfare Technology，2014，29(1):33－37.

［11］曹伟.认知雷达的波形设计算法研究［D］.西安:西安电子科技大学电子工程学院，2011.CAO Wei.The Research on the Waveform Design of Cognitive Radar［D］.Xi’an:College of Electronic Engineering，Xidian University，2011.