基于滑模观测器的电动汽车最大牵引力估计
2015-01-12王晓玉廉宇峰田彦涛
王晓玉,廉宇峰,赵 云,田彦涛,b
(吉林大学a.通信工程学院;b.工程仿生教育部重点实验室,长春130022)
0 引言
节约能源与保护环境是未来汽车发展的方向,因此,纯电动车的研究越来越受到重视。与传统汽油机汽车相比,电动车在控制方面具有转矩响应快速、可实现独立分散控制和可准确测量电机输出转矩的电机电流等优势[1]。这促进了电动汽车在主动安全控制系统的发展。
路面条件的准确估计对电动汽车最大牵引力估计具有重要意义。目前国内外学者对路面条件进行了广泛研究,Hori等[2]提出了基于路面状况估计的牵引力控制系统。在此基础上,Furukawa等[3]提出了电动汽车路面条件估计的新方法,路面条件可由摩擦系数μ和滑移率s曲线特征反映。文献[3]中采用观测器估计各种路面条件,获得最佳滑移率。Vasiljevic等[4]提出了基于轮胎滑移率的牵引力控制系统(TCS:Traction Control System)的在线路面状态条件估计的实验方法。路面条件可使用实时估计的一个函数近似,并用作TCS的输入。该系统的有效性已经得到了验证。Magallan等[5]提出了独立后驱电动汽车最大牵引力控制策略,在不同路面条件下防止车辆打滑。在对路面条件最新研究进展中,Pinar[6]提出了低成本的声学道路类型分类系统,用于汽车主动安全的路面摩擦力估算,该方法的有效性已经通过牵引力控制系统应用程序得到验证。同时,Lin等[7]提出了基于分布式驱动电动汽车的实时估计路面条件的算法,该算法用基于遗忘因子的递归最小二乘法对路面条件估计,结果表明该算法为车辆主动安全控制提供可靠的路面信息。Ge等[8]提出了基于牵引力估计观测器的电动汽车转矩分配控制系统,通过计算智能(CI:Computational Intelligence)的控制器和滑模控制系统获得每个驱动轮参考牵引力。结果验证可提高系统的鲁棒性。杨玉芬等[9]对非均匀点状冰路面状况的观察与分析,为行车安全提供可靠路面信息参考。Chen等[10]提出了一种基于LuGre轮胎模型的实时路面附着系数估计方法,利用观测器估计LuGre轮胎模型的内部状态。用递归最小二乘法(RLS:Recursive Least Square)实时估计路面附着系数,基于整车CarSim模型的仿真结果表明,车辆纵向运动时该系统能可靠地估计路面附着系数。Ren等[11]提出了一种混合方法识别路面条件参数,采用三自由度车辆模型,并采用卡尔曼滤波估计车辆状态信息,进而有效估计路面摩擦系数。Li等[12]提出了新型有效的轮胎路面摩擦系数估计方法,车速和滑移率可通过一种改进的非线性观测器估计,进而获得牵引力矩,仿真实验验证了该估计方法的有效性。同时,为了提高系统的精度,要求准确测量车轮角速度,徐颖等[13]对轮速信号采集系统的研究,为笔者的实验提供了依据。上述研究方法主要针对后驱电动汽车,对四驱的电动汽车研究较少。同时对路面条件的估计一般都采取离线的方式,对系统的实时控制性不强。
笔者在已有研究工作基础上,采用LuGre轮胎动力学摩擦模型和滑模观测器实现在线路面辨识,完成了车辆动力学模型的建立、滑模观测器的设计、根据观测器估计的内部状态变量估算电机输出的最大力矩,进而采用动态饱和非线性控制策略限制电机的最大输出力矩,保证了电动车在不同路面条件下能以最大加速度安全防滑的行驶。
1 车辆动力学
1.1 整车纵向动力学模型
笔者只考虑车辆的纵向运动,不考虑汽车行驶过程中的俯仰运动。车辆纵向动力学模型如下。
1)电动汽车纵向运动方程。考虑车辆行驶在一个水平的路面(见图1),作用于车辆的纵向外力包括空气动力学阻力,纵向轮胎力和滚动阻力。详细描述这些力的方程式如下[14]。
①车辆纵向运动方程
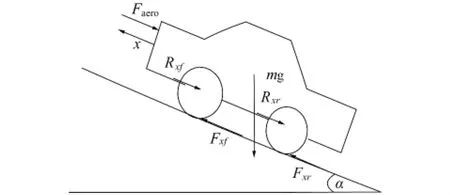
图1 车身受力图Fig.1 Force diagram of the vehicle body

其中m为汽车整备质量(kg);¨x为汽车纵向加速度(m/s2);Fxf为汽车前轮轮胎的纵向力(N);Fxr为汽车后轮轮胎的纵向力(N);Faero为等效纵向空气阻力(N);Rxf为前轮轮胎滚动阻力(N);Rxr为前轮轮胎滚动阻力(N);α为斜坡倾角。
②空气阻力方程
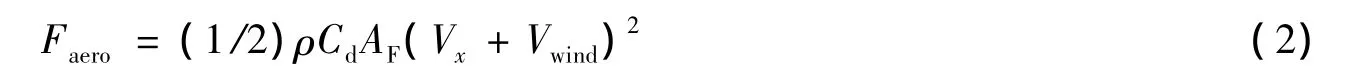
其中ρ为空气的质量密度;Cd为气动阻力系数;AF为汽车前部的迎风面积,即车辆在行驶方向的投影面积;Vx=˙x为车辆纵向速度;Vwind为风速。
③滚动阻力

其中f为滚动阻力系数。
2)电动汽车车轮模型。
①车轮力矩平衡方程。车轮的转动是由车轮力矩平衡方程所决定的。该实验中采用特斯拉双电机四驱结构,特斯拉model X上的四驱系统是在前轴左右轮共用一个驱动电机,后轴左右轮共用一个驱动电机,由中间的电池块提供动力,进而实现四轮驱动(见图2)。

其中J为车轮转动惯量(kg·m2);Td为驱动力转矩(N·m);r为车轮滚动半径(m);Tf=Rxr为滚动阻力距(N·m)。车轮力矩平衡示意图如图3所示。

图2 双电机四驱车辆结构Fig.2 Dual-motor four-wheel driving vehicle structure

图3 车轮力矩平衡示意图Fig.3 The wheel torque balance diagram
②车轮垂直载荷。

其中Fz为车轮垂直载荷(N);h为车辆的质心距离地面高度(m);lf,lr分别为前轴后轴到质心的距离。
1.2 轮胎动力学模型
1)轮胎/路面摩擦系数与滑移率关系。如图4所示,轮胎-路面纵向摩擦系数μ=Fx/Fn为牵引力与法向力的比值,摩擦系数随多种因素的变化而改变,包括路面条件、轮胎气压、垂直载荷、轮胎形状和轮胎滑移率。滑移率

其中r是车轮半径,ω是车轮角速度,vx是车轮线性速度。
图5为μs典型曲线。由图5中可以看出,该曲线中定义了两个工作区间,实验中要控制滑移率在稳定区间内运行。

图4 车轮模型Fig.4 The wheel model

图5 μs典型曲线Fig.5 μs typical curve
2)LuGre轮胎动力学摩擦模型。LuGre轮胎模型可描述如下[15]

其中σ0为轮胎纵向集中刚度系数(m-1);σ1为轮胎纵向集中摩擦的阻尼系数(s/m);σ2为黏着阻尼系数(s/m);μC为库伦摩擦系数;μS为静摩擦系数;vs表示Stribeck摩擦效应的相对速度(m/s);κ表示驱动力分布参数(m-1);vr=ωr-Vx为路面与轮胎的相对速度(m/s);z为轮胎的内部摩擦状态(m);θ为路面条件参数;μ为轮胎与路面的摩擦系数。Fx为地面对轮胎的纵向力,Fn为轮胎所承受的垂直载荷。
该模型的一个重要特征是θ参数不同值代表不同的路面条件。
2 基于滑模观测器的电动汽车路面条件估计
2.1 车辆状态方程
由已建立的车辆模型,定义如下的状态变量

其中zf、zr与驱动轮的LuGre轮胎摩擦动力学模型的内部摩擦状态相对应;Vx为车辆的纵向速度,vrf=rωf-Vx,vrr=rωr-Vx为前后轮胎与路面的相对速度。
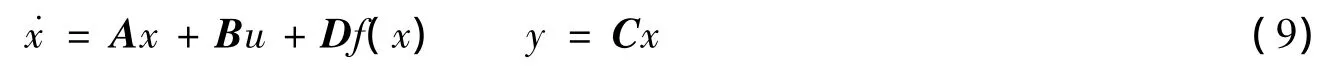
其中包括两部分:线性与非线性。此状态方程的系数矩阵

输入

非线性系数矩阵
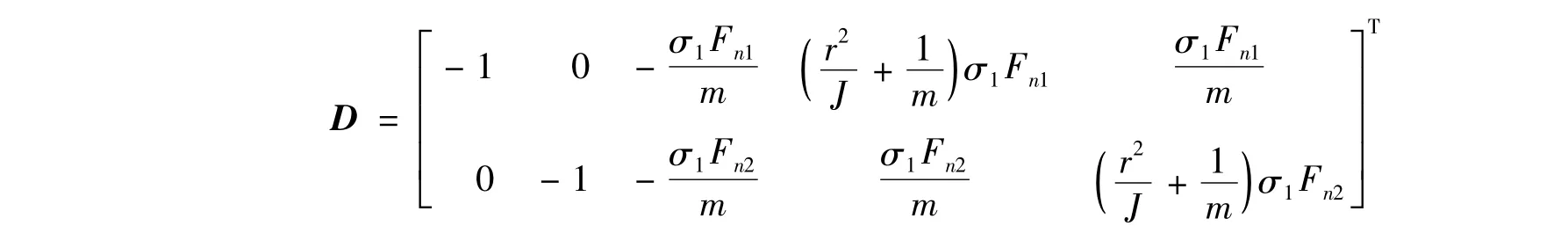
非线性部分
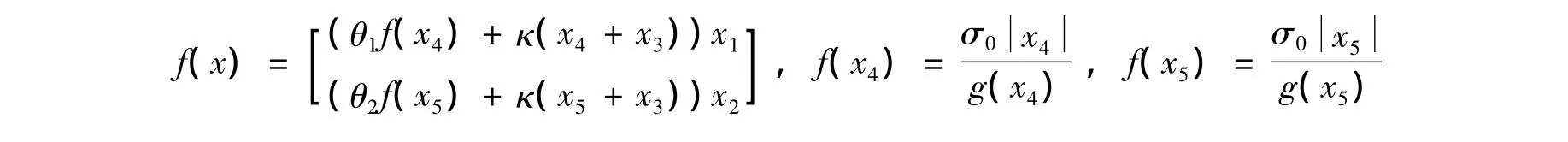
其中Fn1,Fn2分别为前、后轮的垂直载荷;同样θ1,θ2为对应轮胎所在路面条件的 LuGre模型参数;g(x4),g(x5)是式(8)中LuGre模型的g(vr)。
测量上述系统输出的角速度ωf和ωr可用于在观测器设计过程中。
2.2 滑模观测器的设计
根据电动汽车的动力学状态方程,并且车轮的角速度可以测量,提出如下的SMO(Sliding Mode Observer)观测器

其中L是常数增益矩阵;ey是输出估计误差,表达如下

用不连续的向量函数反应滑模运动如下

其中k和F为设计参数。在这个观测结构中,一旦滑动模态稳定,Dν就可以代表系统的非线性f(x)。f(x)包括垂直动力学的影响和参数的不确定性两方面。
在未知输入系统的滑模观测器设计方法中[16],假设非线性项f(x)是有界的,即存在非负实数ρ满足以下条件:对所有x都有估计误差为其中表示x的估计值。因为(A,C)是可观测的,故可在观测系统中找到矩阵L和F,使状态估计误差(e=x-^x)渐进稳定。矩阵L∈Rn×p使矩阵(A-LC)的特征值在左半平面,由(A-LC)(是渐进稳定的)对任意Q=QT>0都仅有1个P=PT>0与其对应,同时选择Q以保证F∈Rm2×p满足如下公式

系统满足式(13),式(14),以确保观测器的可实现。
从上面的估计误差得知,在不确定性Df(x)建模是敏感的。通过文献[17]提出的一个由(A,B,D,C)建立的系统模型的观测器设计可以找到一对矩阵(P,F)满足式(13)和式(14)对应 L和 Q。Edwards等[18]对上述观测器的存在提出充分必要条件如下:
1)rank D=rank CD=r;
其中Q=QT为正定矩阵满足李亚普若夫稳定条件。最后,为使滑动模态稳定和估计误差在有限的时间内趋近零,k应当满足k≥ρ。
2.3 路面参数的估计
一旦进入滑动模态区,状态估计误差趋近零,等效的输出误差信号Dνeq必须保证与方程(9)的非线性部分Df(x)相等,以维持系统的滑模运动。因此

估计的变量趋近于真实值,由式(15)估算得到^θ1,^θ2的表达式如下
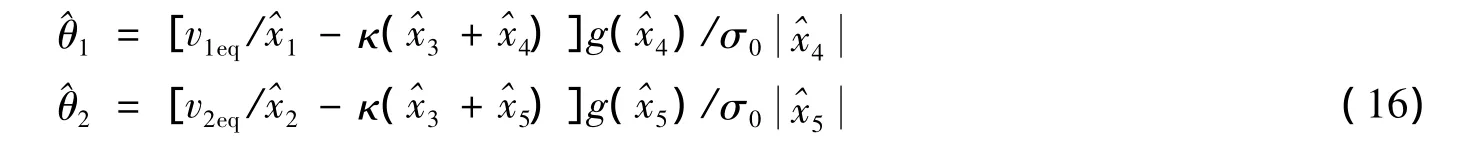
实验中设定一个^θ初始值,避免滑移率为零时打滑现象产生。
2.4 轮胎最大摩擦系数估计
根据上面的路面条件参数^θ和稳态LuGre模型,可以得到稳态的轮胎-路面摩擦曲线μss,通过曲线可以找到最大的摩擦系数μss所对应的最佳滑移。当LuGre模型(8)中˙z≈0时,可得到稳态模型

其中zss和μss为z和μ的稳定值。
得到μss的曲线作为滑移率的一个函数是一组Vx参数化曲线,将w=(vr+Vx)/r代入式(17)可得到μss关于vr的函数如下

为得到最大牵引力,必须计算式(18)中μss的最大值μssmax,可以证明σ2vr的取值几乎不影响μssmax,所以可以忽略。则由∂μss/∂vr=0得到最大值

根据

每个驱动轮产生的最大力依赖于各自摩擦系数的最大值。从状态观测器估计的状态,可确定在任何时间的即时路况,计算出稳定的摩擦系数状态曲线,获得在每个工作点允许的最大摩擦。通过该值确定由电机产生的转矩获得的最大牵引力。
3 牵引力系统控制策略
牵引力控制系统的最大转矩估计主要通过电动汽车电机输出的电磁力矩和转速、车辆加速度等,估计电动汽车的车速、轮胎-路面附着系数和最佳滑移率。通过识别最佳滑移率,计算其对应的最大轮胎摩擦系数μmax,从而由μ=Fx/Fn得到路面可提供的最大牵引力Fxmax,根据路面对每个轮胎可提供的最大牵引力给出每个电机输出的最大电磁转矩T^max,避免了因车轮驱动力矩过大而出现打滑的情况。该方法改善了轮胎与路面附着关系,从而增强了牵引力和汽车的可控性[5]。确定最大转矩的策略如图6所示。图7展示了整个牵引力控制系统的策略。

图6 确定最大转矩的策略Fig.6 The strategy of determining the maximum torque

图7 牵引力控制系统策略Fig.7 The strategy of traction control system
笔者通过对输出力矩的饱和控制完成对汽车牵引力的控制。当滑移率由稳定区间进入不稳定区间时系统能迅速判断是否产生打滑现象,一旦车轮开始打滑,立即减小电磁转矩,保证汽车安全行驶。当滑转现象消失时,又恢复之前以最大牵引力的加速运动。
实验中采用PID对其进行饱和限制,通过实时检测车轮角速度,并计算其相对速度vr,以式(20)估算电机输出的最大力矩作为饱和限制的上限,防止因超过汽车所提供的最大转矩而产生的车轮滑转现象。
4 Matlab/Simulink仿真分析与实验验证
4.1 仿真条件与汽车参数
根据汽车的纵向运动建立的四驱电动汽车模型,表1为电动车的各项参数[5]。
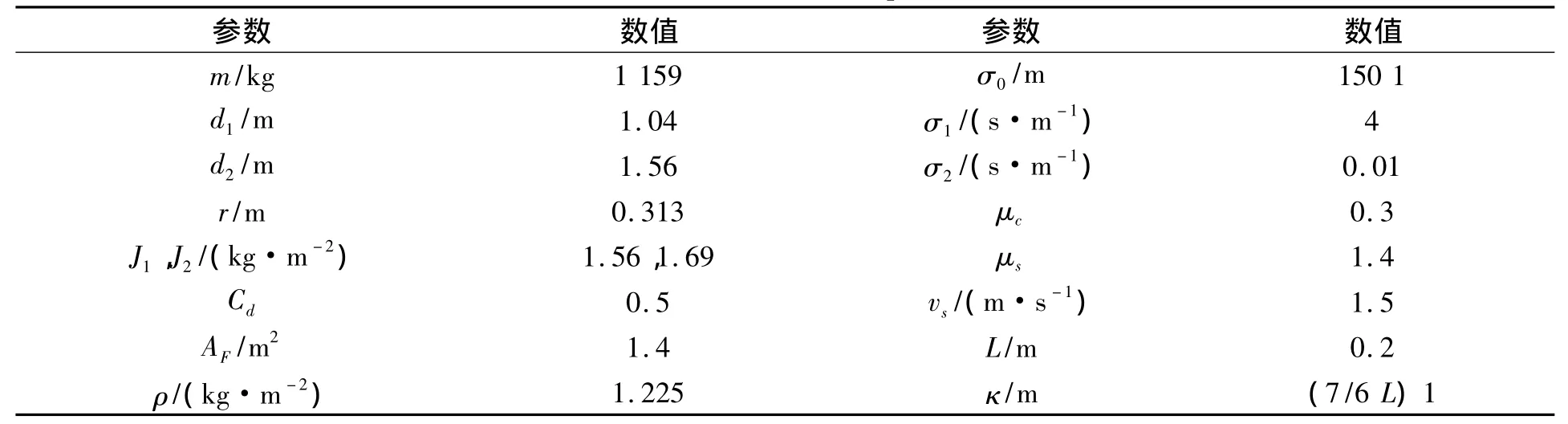
表1 电动车各项参数Tab.1 Electric vehicle parameters
通过观测器设计部分的L与F矩阵具体求法,得出实验采用数据如下

4.2 不同路面条件下汽车加速的仿真分析
实验1 设定不同工况下两组实验对比,分别为α=0°和α=10°时,在t=1 s时改变路面条件,路面条件参数设置为t在0~1 s时,θ=2,设对应的摩擦系数变量为μ1;t在1~2 s时,θ=4,设对应的摩擦系数变量为μ2。将SMO观测得到的状态变量和参数与车辆模型中设定值进行比较分析。
1)当斜坡倾角α=0°时,得到的车辆状态的各个量变化曲线图如图8所示。
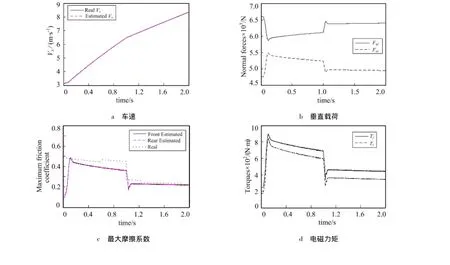

图8 车辆行驶在水平路面时的状态参数变化曲线Fig.8 Vehicle state parameter change curve in a horizontal pavement
2)当斜坡倾角α=10°时,可得到的车辆状态的各个量变化曲线图如图9所示。

图9 车辆行驶在斜坡倾角为10°路面时的状态参数变化曲线Fig.9 Vehicle state parameter change curve in a slope angle of 10°pavement
从图8、图9可看出,在不同工况作用下,当路面条件发生变化时系统能快速识别,并且控制效果很好。最大摩擦系数曲线和滑移率曲线的真实值和估计值均在所能达到最大值范围内,可保证车辆安全不打滑行驶。同时,当有斜坡倾角时,图9a中Vx加速过程相对图8a变缓,转矩和牵引力变化趋势保持不变,都随最大摩擦系数变化而变化。
实验2 通过对系统进行有路面条件估计和没有路面条件估计的对比实验,验证控制系统的有效性。倾斜角α=0°,且汽车的输入加速度为3 m/s2。当在行驶过程中车轮出现极端打滑现象时(滑移率超过20%),控制量清零,从而保证汽车行驶的安全性。实验结果如图10所示。

图10 没有路面条件估计时车辆行驶状态曲线Fig.10 Vehicle state curve with no pavement condition estimate
由图10可以看出,当没有路面条件估计时,路面条件发生变化时系统不能识别,车辆不能迅速做出反应调节这种改变,会使汽车产生打滑现象。有路面条件估计时,系统在路面条件变化时能保证车辆安全防滑行驶,验证了笔者控制方法的有效性。
5 结语
笔者提出了一种双电机四轮驱动的电动汽车最大牵引力估计的方法,它是在LuGre摩擦动力学模型和SMO研究的基础上建立起来的。经实验验证在汽车直线行驶过程中,该控制策略对突然改变路面条件参数情况,能迅速作出反应,同时所做的对比试验充分证明所搭建模型的有效性;在没有路面条件估计时,电动车在路面条件变化时会产生打滑和不稳定运行。该系统能实时根据估计的路面条件合理分配驱动力矩,保证汽车能在获得最大驱动力的情况下安全稳定的行驶。
[1]MAEDA K,FUJIMOTO H,HORI Y.Four-Wheel Driving-Force Distribution Method Based on Driving Stiffness and Slip Ratio Estimation for Electric Vehicle with In-Wheel Motors[C]∥IEEE Vehicle Power and Propulsion Conference.Seoul,Korea:[s.n.],2012:1286-1291.
[2]HORI Y,TOYODA Y,TSURUOKA Y.Traction Control of Electric Vehicle Based on the Estimation of Road Surface Condition-Basic Experimental Results Using the Test EV UOT Electric March[C]∥Power Conversion Conference.Nagaoka,Japan:[s.n.],1997:1-8.
[3]FURUKAWA K,HORI Y.Recent Development of Road Condition Estimation Techniques for Electric Vehicle and Their Experimental Evaluation Using the Test EV“UOT MarchⅠ andⅡ”[J].Industrial Electronics Society,IEEE Transaction on,2003(1):925-930.
[4]VASILJEVIC G,GRIPARIC K,BOGDAN S.Experimental Testing of a Traction Control System with on-Line Road Condition Estimation for Electric Vehicles[C]∥21st Mediterranean Conference on Control& Automation(MED).Chania,Greece:[s.n.],2013:296-302.
[5]MAGALLAN G A,ANGELO C H D,GARCIA G O.Maximization of the Traction Forces in a 2WD Electric Vehicle[J].Vehicular Technology,IEEE Transaction on,2011,60(2):369-380.
[6]PINAR BOYRAZ.Acoustic Road-Type Estimation for Intelligent Vehicle Safety Applications [J].International Journal of Vehicle Safety,2014,7(2):209-222.
[7]LIN Cheng,WANG Gang,CAO Wanke,et al.Real-Time Estimation of Road Friction Coefficient for the Electric Vehicle[C]∥The Third World Congress on Software Engineering(WCSE).Wuhan,China:[s.n.],2012:172-175.
[8]GE Yinghui,CHANG C S.Torque Distribution Control for Electric Vehicle Based on Traction Force Observer[J].Computer Science and Automation Engineering,IEEE Transaction on,2011(2):371-375.
[9]杨玉芬,李明明,高晓旸.基于Virtual Box非均匀点状冰路面的安全性分析[J].吉林大学学报:信息科学版,2013,31(2):173-176.YANG Yufen,LI Mingming,GAO Xiaoyang.The Non-Uniform Dotted Ice Road Safety Analysis Based on the Virtual Box[J].Journal of Jilin University:Information Science Edition,2013,31(2):173-176.
[10]CHEN Yan,WANG Junmin.Vehicle-Longitudinal-Motion-Independent Real-Time Tire-Road Friction Coefficient Estimation[C]∥The 49thIEEE Conference on Decision and Control(CDC).Atlanta,USA:[s.n.],2010:2910-2915.
[11]REN Hongbin,CHEN Sizhong,TAEHYUN SHIM,et al.Effective Assessment of Type-Road Friction Coefficient Using a Hybrid Estimator[J].Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility,2014,52(8):1047-1065.
[12]LI Boyuan,DU Haiping,LI Weihua.Comparative Study of Vehicle Type-Road Friction Coefficient Estimation with a Novel Cost-Effective Method [J].Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility,2014,52(8):1066-1098.
[13]徐颖,刘磊,赵旗,等.ABS实时四轮轮速信号采集系统[J].吉林大学学报:理学版,2009,47(5):977-980.XU Ying,LIU Lei,ZHAO Qi,et al.The ABS Real-Time Four-Wheel Wheel Speed Signal Acquisition System [J].Journal of Jilin University:Science Edition,2009,47(5):977-980.
[14]RAJESH RAJAMANI.Vehicle Dynamics and Control[M].New York,United States of America:Springer,2006.
[15]PANAGIOTIS TSIOTRAS,EFSTATHIOS VELENIS,MICHEL SORINE.A LuGre Tire Friction Model with Exact Aggregate Dynamics[J].Vehicle System Dynamic,2004(42):195-210.
[16]HUI S,ZACK S H.Observer Design for Systems with Unknown Inputs[J].Mathematics and Computer Science,2005,15(4):431-436.
[17]WALCOTT B,ZAK S H.State Observation of Nonlinear Uncertain Dynamical Systems [J].Automatic Control,IEEE Transaction on,1987,32(2):166-170.
[18]EDWARDS C,SPURGEON S K.Sliding Mode Control:Theory and Applications[M].London:Taylor and Francis,1998.
