例说促进初中生数学概念理解的教学途径

2015-01-12西藏昌都市察雅县中学李江专

新课程研究 2015年31期

◆ 西藏昌都市察雅县中学李江专

例说促进初中生数学概念理解的教学途径

◆ 西藏昌都市察雅县中学李江专

概念教学是初中数学一项重要的教学内容，掌握好数学概念是推导定理，掌握数学公式、法则的基础。本文以数学概念的教学实例为基础，提出3种概念教学途径：从借助直观到抽象概念的变式教学，数学概念的非概念变式教学，数学概念的形成过程的变式教学。旨在促进初中生对数学概念的理解，对初中数学教师的概念教学有所启发。

初中数学；数学概念；概念教学

数学概念教学是初中数学教学的一项重要内容，学生掌握好数学概念是推导定理，掌握数学公式和法则的基础。在数学概念教学中，教师采用什么教学方法和途径尤为重要。如何进行数学概念教学呢？下面通过一些实例来阐述在初中数学教学中，促进初中生对数学概念理解的方法和途径。

一、从直观到抽象的变式教学，旨在理解数学概念

数学概念的一个基本特征是抽象性。学生理解抽象的概念往往感到空洞，从而影响他们准确掌握概念的内涵和本质。事实上，初中许多数学概念直接来自具体的感性经验，所以，寻求数学概念在生活中的根源，挖掘数学概念的本源，很有必要。这就启发我们，对初中数学概念的教学，关键是要让学生建立起感性经验与抽象概念之间的关联。

例1 相似三角形概念的教学

数学源于生活。在教学过程中，我们不妨采取直观变式的教学方式，将抽象概念的教学建立在学生已有的感性经验基础上，让生活中的具体实物与抽象的数学概念之间建立起有效联系。

图1.1 生活中的相似三角形

首先，教师呈现日常生活中的直观图片素材，如图1.1生活中的相似三角形。这样能发挥学生已有的感性经验，使学生理解相似三角形的初步含义。

图1.2

第二，用不同图形的变式，如图1.2，作为直观材料和抽象数学概念之间的过渡，使学生原有的感性经验上升到相似三角形概念的认识。

最后，在此基础上，提出相似三角形的概念。

例2 算术平方根概念的教学

教师将正方形面积和边长的关系（见表1.1）先呈现给学生，在此基础上，给出表1.2算术平方根，这样来引入算术平方根的概念。

这里的“算术平方根”，对刚入学的初中生来说，虽然是抽象的数学概念，但是他们容易理解正方形面积和边长的关系。正是在正方形面积和边长的关系这种现实直观和具体数据的作用下，学生能建立起有效联系，从而帮助其理解算术平方根的含义。

表1.1 正方形的面积和边长的关系

表1.2 算术平方根

例3 平行线概念的教学

有观点认为，数学是“看”出来的。这种观点借用在数学概念的教学中，教师采用直观或具体图形的变式教学，学生在学习中从直观到抽象的认识，从而“看”出数学概念的内涵。

平行线的概念，教师可以从学生熟悉的现实生活实例入手，如：铁轨、高压线上的两根电线、黑板的上下边缘等。用日常生活中所接触到的实物、图形等作为学生认识的感性材料，再让学生通过观察、分析、比较、归纳和概括，从而掌握平行线的属性，实现平行线概念的教学目的。

二、通过非概念的变式教学，旨在挖掘数学概念的内涵

要让学生理解数学概念的内涵，通过非概念的变式教学，让学生明确概念的外延，也就是先让学生辨别数学概念相对的一面，从而达到掌握数学概念属性的意图。

例4 邻补角概念的教学

图2.1 邻角的概念图

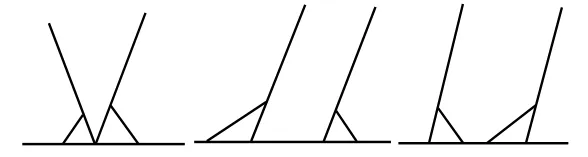
图2.2 邻补角的非概念图

用多媒体呈现图2.1邻补角的概念图形和图2.2邻补角的非概念图形。

师：图2.1中的两个角是邻补角，而2.2中的3对角都不是邻补角。对照比较，你能发现什么是邻补角呢？

生1：邻补角必须要有一条公共边。

生2：有一个公共顶点。

生3：一个角的一边是另一个角的反向延长线。

……

师：互为邻补角的两个角一定互为补角吗？互为补角的两个角不一定互为邻补角吗？

教师借助了邻补角的非概念的3种反例图形，以提问的方式让学生观察、比较、思考，从而描述出邻补角的内涵和外延。教师通过对邻补角的概念图和非概念图的变式教学，从而使学生掌握邻补角的概念。

例5 圆的切线概念的教学

用多媒体呈现图2.3圆的切线概念图和图2.4圆的切线非概念图。

师：图2.3中的直线是圆的切线，而图2.4中的直线都不是圆的切线。那么圆的切线是什么呢？

生1：虽然直线垂直圆的半径，但没有经过圆的半径的外端。

生2：虽然直线经过圆的半径，但没有垂直于圆的半径。

生3：直线与圆没有交点。

……

师：你能总结出圆的切线要满足哪两个条件吗？

在教师的引导下，学生通过对圆的切线非概念图的探究、归纳，得出圆的切线要满足的两个条件：经过半径的外端，垂直于这条半径。这样学生就很容易理解和掌握圆的切线的概念。

图2.3 圆的切线概念图

图2.4 圆的切线非概念图

三、通过概念形成过程的教学，旨在揭示数学概念的本质

早有研究者提出“过程性变”的概念。过程性活动变式是，在数学活动过程中，通过有层次的推进，使学生分步解决问题，积累多种活动经验，让学生体验数学概念的形成过程，从而掌握数学概念，揭示数学概念的本质。

例6 二次函数有关概念的教学

二次函数是初中数学重要的教学内容，二次函数一般式的形式、二次项系数等既是重点，又是关键。若教师只是简单地让学生记住二次函数的解析式，而学生并没有真正掌握二次函数的来龙去脉，会让学生感觉到数学就是机械记忆。既然二次函数来自现实生活，必然能用生活中的实际问题来确定二次函数的解析式。在二次函数概念教学中，教师不妨抓住二次函数在现实生活中的事例，让学生体验二次函数概念的形成过程，既可让学生主动参与，积极探索，又能准确掌握二次函数的有关概念。

师：在下列问题中，求x与y的关系式。

①正方体的边长为x，表面积为y；②正方形的边长为x米，边长增加2米，边长增加之后的正方形的面积为y；③圆柱体的底面半径为x米，高为4米，其体积为y；④操场上有y名学生做课间操，恰好站成长方形，有x排学生，纵排比横排多2。

生：①y=6x2；②y=x2+4x+4；③y=4πx2；④y=x2+2x

师：这4个关系式有什么共同特点？

生：（通过观察、比较），都有二次项。

师：他们都是函数吗？

生：是。

师：给此类函数取个名。我们就把它称为二次函数。假若二次项前面的系数为零，能确保有二次项吗？

生：不能。

师：理由是什么呢？

生：若二次项系数为零，就没有二次项了。

通过教师的引导，归纳出二次函数的一般形式：y=ax2+bx+c （a≠0）以及当b=0、c=0时，y=ax2（a≠0）是特殊的二次函数，学生从而掌握了二次函数的结构特征，掌握了二次函数的有关概念。