让“问题的灵魂”入驻解题的精髓——在开放题解题中培养学生能力的教学策略

◆ 安徽省六安市三里桥小学 王 林

让“问题的灵魂”入驻解题的精髓
——在开放题解题中培养学生能力的教学策略

◆ 安徽省六安市三里桥小学 王 林

“数学开放题，是指那些答案不唯一，并在设问方式上要求学生进行多方面、多角度、多层次探索的数学问题”（戴再平语）。“提出一个问题往往比解决一个问题更重要 ”。发现问题是数学思维活动中的一个重要发端，没有问题的发现，一切数学思维都是浮云。提出问题建立在发现问题的基础之上，经过沉淀积累，运用一定的逻辑思维，通过语言的有序组织表达出来。教学中的最大问题是学生没有问题。只有当学生能够独当一面，自己有能力去发现问题并提出问题的时候，学生才真的成了学习的主人。生活离不开数学。这就要求我们的数学课堂是个探索者的舞台，积极引导学生去发现问题、提出问题。

开放题；发现问题；提出问题；教学策略

在数学开放题解题训练中，如何培养学生发现问题、提出问题的能力，成为一线教师的痛。很多教师在教学中，把数学开放题放入“奥数”中，走“奥数”的路子，让学生误认为开放题就是“奥数”。也有老师把开放题当作“应用题”教学，通过记题型、打“题海战”来巩固知识。这样做就使开放题的功能大打折扣，得不偿失。

数学开放题，是指答案不唯一，并在设问方式上要求学生进行多方面、多角度、多层次探索的数学问题（戴再平语）。由此可见，在数学开放题解题训练中，培养学生发现问题、提出问题的能力，显得尤为重要。要让学生从关注问题解答转向关注发现问题、提出问题以及问题解决，而答案放到最后关注。因为“提出一个问题往往比解决一个问题更重要 ”（ 爱因斯坦语）。

“问题是数学的心脏”，而发现问题是数学思维活动中的一个重要的发端，没有问题的发现，一切数学思维都是浮云，终究会被“肤浅的风”吹散。提出问题建立在发现问题的基础之上，经过沉淀积累，运用一定的逻辑思维，通过语言有序组织地表达出来。教学中的最大问题是学生没有问题，只当教师的附庸和知识的存储器。只有当学生能够独当一面，自己有能力去发现问题并提出问题的时候，学生才真的成了学习的主人。运用大脑勤于思考、善于思考，最终成为独具魅力的一个学习的行者，而不是人云亦云。

那么，在开放题解题训练中，培养学生发现问题和提出问题的能力有哪些策略呢？

一、营造解题 “气场”：让学生敢于发现问题、提出问题

人之所以会思考，是因为发现了问题，问题是思维的开始。 “疑是思之始，学之端。”学贵有疑，有疑才有思；思有所得，趣必生之，兴趣是学习的最好老师。在开放题解题教学中，教师要持续不断、热情洋溢地鼓励学生发现问题、提出问题。当然，作为数学学习活动的组织者、引导者与合作者，教师要努力为学生创设学习情境，让学生在数学开放题的解题过程中，成为问题的发现者和提出者。

“成功的教学依赖于一种真诚的尊重和信任的师生关系，依赖于一种和谐安全的课堂气氛”（美国心理学家罗杰斯语）。只有在其乐融融的学习“气场”中，学生才会彻底放松自己，发挥潜能。刚开始学生发现问题、提出问题可能是稚嫩的、荒唐的，甚至是错误的，但教师都要满腔热情地呵护，因为出错是学生的权利。一个肯定的眼神，一个赞许的手势，一句及时的点评，一个会心的微笑……都会让学生产生愉悦的心理体验，感受思考的价值，收获成功的体验。学生发现问题、提出问题的热情会进一步高涨。

笔者曾经听过一位老师上《组合图形的面积》这一课。课尾的时候，一个学生兴致勃勃地问了这样一个问题：“我家最近在装修房子，剩下了一块L形的木板，工人师傅想用一条直线把它分成面积相等的两部分，可是，一时还没有想到办法，就放在一边不用了，不知道老师有没有办法？”

这是一道开放题，此问题一出，课堂荡起了涟漪，好似春风吹皱了一池春水。教师比画了几下，好像没有把握，就告诉学生，这个问题下课以后再讨论。问题被轻轻带过……

学生发现问题、解决问题的思维火花，就这样被教师轻描淡写地熄灭了。如果这位老师能够重视这个开放题，营造好“气场”，从课堂上挤出一点时间来探讨这个问题，哪怕只是开个头，都是好的。如果实在没有时间，可以做个“引子”，吊起学生学习的胃口，引导学生课下深入研究。如此一箭多雕，岂不妙哉？

二、解题“缓说破”：从“自悟”中发现问题、提出问题

老师很可爱，出现了一个问题就迫不及待地要学生回答，如果学生卡壳了，或者出现了短暂的冷场，就积极暗示、提醒，直到问题解决了，没有留给学生“自悟”的时间和空间。

不过，咱们这里所说的“自悟”，是指开放题出现后，教师先不做任何提示，让学生自读自悟，自己从中寻找问题、提出问题。经历：调动已有的知识经验，与开放题相比较，上串下联，发现问题；从开放题的性质、意义、特征、规律等方面发现问题、提出问题；从开放题的算理、解法以及关键的字词句上发现问题、提出问题；从困惑、解释不清、认识模糊处入手，发现问题、提出问题。

数学来源于生活，又服务于生活，生活离不开数学。这就要求我们的数学课堂是个探索者的舞台，积极引导学生去发现问题、提出问题。数学课堂要完成这个艰巨的任务，需要一个合适的脚手架、一个顺手的载体，开放题因其独特的内涵受到了人们的青睐，成为培养学生发现问题、提出问题能力的有力助推器。利用生活中的问题，合作学习，提供时间和空间，引导有效提问等方式，在开放题解题中培养学生发现问题和提出问题的能力。

比如上例说到的“L形木板”问题，“工人师傅想用一条直线把它分成面积相等的两部分，可是，一时还没有想到办法”。让学生说，要解决这个问题，你有什么问题，你还有什么疑问，你可能从哪里入手等。学生可能会觉得这是一个不规则的图形，如果是规则图形就好办了，从中一分为二……

能不能把不规则的“L”形变成规则的图形呢？于是，学生发现了分割、贴补。（如下图），甲图可以割补成乙图、丙图和丁图。

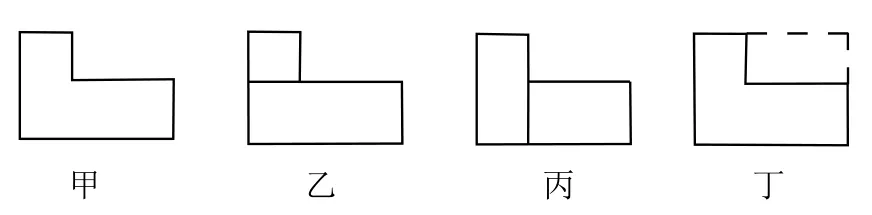
至此，对于这个开放题，学生已经发现了问题、提出了问题，“缓说破”实现了其战略意图。学生的探究目标明确了，至于问题怎么解决，后面还会说到，在这里不再赘述。

三、 解题“趟着走”：在尝试中发现问题、提出问题

学生是学习的主体，学生学习新知是经过对新知的尝试发现，以及对新知的意义主动建构完成的。这个过程，经历了新老知识、经验的碰撞，学生主动完成了知识的建构，而且是主动建构。

在开放题解题过程中，教师要大胆放手，让学生去尝试。当新旧知识之间产生冲突，对同一个问题，不同的学生会发表不同的看法，当大家各不相让的时候，教师适时介入，点拨学生发现问题、提出问题。

例如上例“L形木板”问题。当学生把木板割补成规则的图形后，发现问题还是没有解决，还是不知道从哪里到哪里画一条直线，才能把木板分成面积相等的两部分。

在经过前期的学习铺垫后，教师适时点拨，会起到四两拨千斤的作用。

下面是一个教师的教学片断：

师：一条直线把一个平面图形分成面积相等的两部分，这条直线一般会经过哪个点？

生：中心点。

师：如何寻找中心点？

生：以前做过，十字交叉法……

师：每个规则的图形都有中心点吗？

生：是……（学生有些犹豫）。

（教师引导学生看长方形、正方形、梯形等图形的中心点）

师：直线经过这个图形的——

生：中心点……

师：到底对不对呢？接下来——

生：验证！

……

于是，小组合作学习之后，学生得到了以下的图形：

让学生总结，推广方法：

解答该题的关键：把这个组合图形割补成规则的图形，然后找到这两部分的中心点，最后连接这两个中心点，即可达到目标。发现规律，传授方法。

在尝试中前进，在主动中学习，在问题解决中愉悦身心。学生的情商、思维能力都得到了进一步的提高。

四、“做过的理解了”：在操作中发现问题、提出问题

有人说，听过的忘记了，看过的记住了，做过的理解了。“手是意识的伟大培育者，又是智慧的创造者”（苏霍姆林斯基语）。帮助学生由具体形象思维过渡到抽象逻辑思维的必要手段，就是让学生动手操作。反之，通过动手操作，也可以把抽象的思维以具体的形式表现出来。

例如，让学生用9根火柴棒拼三角形，起点低，学生人人都能参与，都能拼出图形，但要拼的多、全，则需要寻找方法、发现规律。在尝试操作、感悟探究的基础上，逐步完善拼图类型。

那么，按什么分类？（按照大小、个数、是否有公共边……）如何拼多、拼全？大胆猜想，小心求证。

首先展示学生的作品，然后点评，引导学生观察、判断（火柴棒重合的、首尾不衔接的……），最后分类（符合要求但重复的图形去掉后分类），学生最终拼成了这样的图形（如图）。

小组汇报后，指名说巧拼三角形的方法。

再比如，让学生做个圆锥体。看似简单活动，做起来并不简单。底和“圆锥帽”（学生语）不好合起来，要么大了，要么小了。经过多次试验，学生发现了画这样的图（图），再做圆锥就省事多了（接头忽略不计）。外面是个正方形，半圆的直径等于正方形的边长，小圆的直径等于正方形边长的一半。

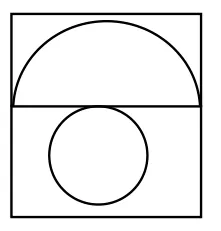
通过探究，培养学生发现数学问题、提出数学问题的能力, 改变以往发现问题、提出问题由教师包办代替的传统教学模式，尊重学生已有的知识、生活经验，给学生时间和空间，鼓励学生积极主动地发现问题、提出问题，大胆尝试，在观察、操作、探究等过程中发现问题、提出问题，以及解决发现和提出的问题。解决生活中的一些数学问题，积极挖掘有思考价值的实践活动。当然，也可在情境中模拟，锻炼学生发现问题、提出问题和问题解决的能力，激发学生的创造潜能。

在开放题解题教学中，老师们不仅要指导学生学会观察，还要让学生参与实践活动。当然，这些情境的素材选择应尽量都来自于生活，让学生感受到“生活中处处有数学”，渗透开放题的问题意识，培养学生发现问题、提出问题的习惯。

在开放题解题中培养学生发现问题和解决问题的能力，其重中之重是学生的主动参与，学生是主体，教师适时点拨，为其保驾护航。不急于求成，循序渐进，高调鞭策学生发现问题、提出问题。从多方位、“立体式”地激励不同层次的学生积极参与，以小组合作形式，助推学生人人成长。教师积极评价学生的行为，寻找“闪光点”，让学生品尝成功的滋味、胜利的喜悦，让“问题的灵魂”入驻解题的精髓，让孩子们从小就变成一个“发现问题、提出问题” 的人。

[1]义务教育数学课程标准数学课程标准[M].北京：北京师范大学出版集团.2011.

[2]戴再平等.数学开放题研究[M].广西：广西教育出版社.2012.

[3]杨传冈等.小学数学开放题举一反三[M].南京：南京大学出版社，2014.

[4]窦桂梅、顾明远等.基于学生发展素养的“1+X课程”专辑[J].人民教育，2015（13）.

[5]郑毓信.开放题与开放式教学[J].中学数学教学参考，2001（3）；中国人民大学复印资料G35；中学数学教学，2001（11）.

（策划组稿：杨传冈 编辑：胡 璐）

王林，特级教师，中学高级教师，市优秀教师，教育部师范大学基础教育课程研究中心“优秀教师”。 中国教育学会数学教育研究发展中心会员，省、市数学理事会理事，“十五”重点课题《规范基础教育学制，促进课程改革与素质教育的研究》先进工作者，中央教育科学研究所教育与人力资源研究部论文一等奖获得者。编著丛书及专著，并发表文章数百篇。

本文系全国教育规划“十二五”教育部重点课题“数学开放题对小学生思维发展的具体影响评测”研究成果，项目编号：DHA140327

G623.5

A

1671-0568 （2015） 31-0088-03