混凝土梁斜拉桥粘滞阻尼器参数分析

杜世界

（同济大学建筑设计研究院（集团）有限公司，上海市 200092）

0 引言

随着我国经济的高速发展和城市化进程的加快，桥梁工程的建设技术也在日新月异地进步，跨江跨海的斜拉桥修建得越来越多。这些桥梁一般都占据着交通网络枢纽的重要位置，是交通生命线的重要组成部分。从近几年来发生在世界各地的地震震害来看，处于交通网络枢纽的重要桥梁一旦发生破坏将导致更为严重的次生灾害[1,2]。因此，如何提高这类桥梁结构的抗震性能一直是工程技术人员研究的重点。近年来，通过设置粘滞阻尼器来改善斜拉桥的抗震性能正在成为一个研究和应用的热点，并在许多实际工程实例中进行应用[3,4]。这些工程实例多为跨径400 m以上的斜拉桥，主梁多采用钢梁或钢-混凝土组合梁。对于斜拉桥来说，400 m以下跨径一般采用混凝土主梁相对更为经济。混凝土主梁斜拉桥梁体质量较大，在地震作用下可能产生更大的地震响应。而在国内，就粘滞性阻尼器在混凝土主梁斜拉桥结构抗震中的应用所开展的参数研究还比较少。本文以某越江大跨度混凝土斜拉桥为工程背景，研究通过在纵桥向设置粘滞阻尼器来提高该桥纵桥向抗震性能，并就阻尼器的参数确定进行分析，得到的参数变化规律可供该类工程应用参考。

1 非线性粘滞阻尼器

典型的粘滞阻尼器如图1所示。液体粘滞阻尼器设计一般采用双出杆油缸式结构，由缸体、导杆、活塞、阻尼孔、粘滞流体阻尼材料组成。活塞在缸筒内作往复运动，活塞上有适量的小孔成为阻尼孔，缸筒内装满粘滞流体阻尼材料。活塞的往复运动带动内部硅油的流动，分子产生相对运动不可恢复，分子之间产生内摩擦力，进而转换成热能；另外内部流体与固态缸体表面的摩擦力转换成热能，这样将地震能转化为分子热能，进而产生阻尼效果，达到耗能的目的[5]。

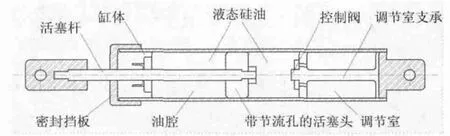
图1 粘滞阻尼器构造图

粘滞阻尼器同其他减隔震装置相比，其优点在于：（1）阻尼器内置为液体，本身没有可计算的刚度，不影响整个结构原有的设计和计算（如周期，振型等），也就不会产生预想不到的副作用；（2）安置在结构上的粘滞阻尼器在最大位移的状态下受力为零，最大受力情况下位移为零，这一性能对减小结构反应十分有利；（3）粘滞阻尼器既可以降低地震反应中的结构受力也可以降低反应位移。

粘滞阻尼器的阻尼力与相对变形可通过下列公式求得[6]：

其中：F为阻尼力，以k N为单位计；V为阻尼器冲程速度，以m/s为单位计；α为阻尼指数，对于粘滞性阻尼器，一般取用0.2～2.0范围；C为阻尼系数，其单位为kN，即在1 m/s的基准运动相对速度下粘滞阻尼器产生的阻尼力。

粘滞阻尼器的阻尼力-速度关系曲线如图2所示，当α=1时称为线性阻尼；当α＜1时称为非线性阻尼，在速度较小时即可产生较大的阻尼力，而当速度较大时，阻尼力的增幅则较小；当α＞1时称为锁阻尼，情况与α＜1时恰好相反，速度较小时，阻尼器的阻尼力很小，而当速度较大时，阻尼力的增加也很快。在桥梁抗震设计中，这三种阻尼装置均有应用，对于线性阻尼和非线性阻尼，其阻尼力与位移的滞迴曲线比较饱满，其减震原理为对地震能量进行耗散；对于锁阻尼，其主要作用是对安装滑动支座的桥墩在地震作用下墩梁相对运动速度超过一定阈值时进行锁定，形成多个固定支座后使地震作用平均分配到各个桥墩。对于双塔斜拉桥来说，其结构惯性质量大，振动周期长，地震作用输入结构体系的能量巨大，且其结构体系一般为漂浮或半漂浮体系，各索塔本身即为共同承受地震作用，采用粘滞阻尼器的主要目的则是耗散地震作用产生的巨大能量，因此通常采用线性阻尼和非线性阻尼。

图2 粘滞阻尼器阻尼力-速度关系曲线图

2 工程背景

2.1 工程概况

某越江大跨度混凝土斜拉桥位于上海市西南片区，是区际公路干线上一个的重要越江工程节点，大桥为主跨296 m的双塔双索面半漂浮体系斜拉桥，桥梁跨径组合为48+77+296+77+48=546（m）。桥面宽度34.6 m，H型钢筋混凝土桥塔，承台以上塔高92.2 m，桥面以上塔高76 m。主梁标准截面采用预应力混凝土双主肋断面，主梁宽度34.6 m，顶面在车行道范围内设2.0%双向横坡，布索区和人非混行道为平坡。主梁中心高度2.8 m，主梁肋处梁高2.55 m，主梁梁高全桥不变。桥梁总体布置图和主梁横断面尺寸如图3、图4所示。

图3 某越江大跨度混凝土斜拉桥总体布置图

2.2 计算模型

根据桥梁结构的总体构造，建立了结构动力特性与地震反应分析的三维有限元模型，如图5所示。其中，主梁、索塔、边墩和辅助墩均采用空间梁单元模拟；斜拉索采用空间桁架单元模拟，并考虑由于垂度效应引起的几何刚度影响；桩基础考虑以m法计算索塔、桥墩基础的地基刚度，考虑桩基的弯剪耦合效应，以6×6弹性地基刚度矩阵进行模拟。粘滞阻尼器的力学特性则采用专门的单元以Maxwell模型进行模拟.

2.3 地震输入

结构地震输入采用该斜拉桥新建工程的场地地震安全性评价报告提供的地震动参数。该报告对于各种概率水准的地震作用均提供4组人工合成水平向和竖向地震动加速度时程。本文阐述的均以地震超越概率为50 a2%（地震重现期2 450年）的4组地震动加速度时程进行分析，并对结构响应取包络值进行研究。其中一条地震波的加速度时程与其3%阻尼比的加速度反应谱如图6、图7所示。

3 阻尼器参数分析

根据对粘滞阻尼器力学性能的介绍与分析可知，当粘滞阻尼器的参数选取不同时，粘滞阻尼器对结构的影响也不相同。因此，需要考虑对阻尼器的阻尼参数和阻尼指数进行敏感性分析。研究这些参数变化对结构响应影响的变化规律，为粘滞阻尼器设计参数的确定提供依据。

通过对结构体系的仔细考虑，根据该桥结构设计特点，为使梁体、索塔受力对称均衡，该桥在每个索塔与主梁间设置4个纵向粘滞性阻尼器进行减震，全桥共设置8个阻尼器。以上文所述的4组地震加速度时程进行非线性时程分析，分析工况见表1所列。

图4 主梁横断面构造图

图5 结构动力分析模型

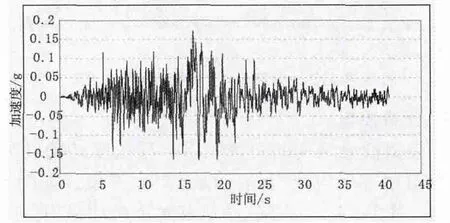
图6 地震波加速度时程图示

图7 地震波反应谱

表1 阻尼器参数分析工况一览表

综合考虑结构各个关键部位响应量的情况,一方面利用阻尼器降低结构关键部位的位移，避免结构可能发生的碰撞破坏，同时又考虑利用阻尼器降低结构关键部位的内力响应，通过比较分析这些响应量来确定粘滞阻尼器的合理参数。具体的计算结果及其随阻尼器参数变化的规律见图8～图13所示。

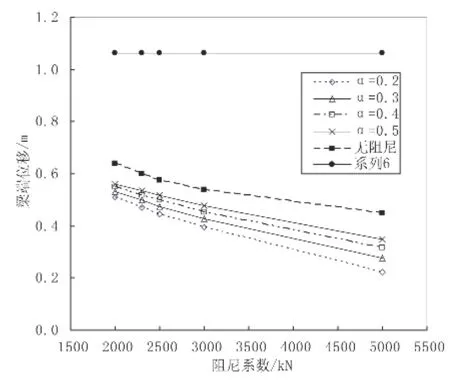
图8 主梁梁端位移曲线图

图9 索塔塔顶位移曲线图

图10 索塔塔底弯矩曲线图

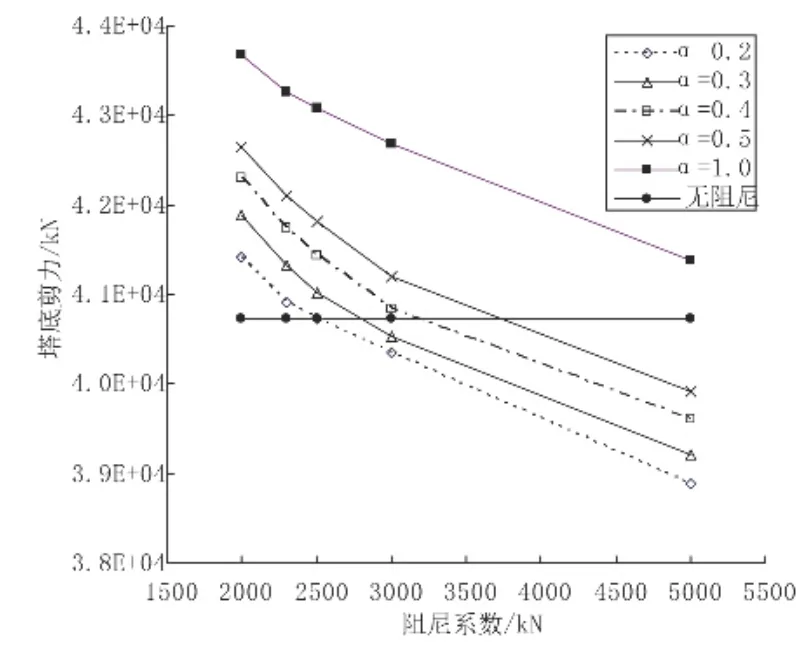
图11 索塔塔底剪力曲线图

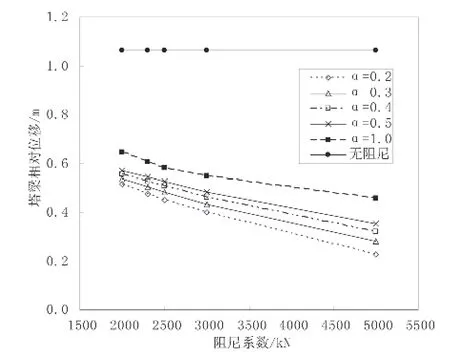
图12 塔梁间相对位移曲线图

图13 阻尼器最大阻尼力曲线图

图8、图9所示为不同阻尼器参数情况下主梁梁端与索塔塔顶最大位移的变化规律。从图中可以看出：在不设纵桥向阻尼器时，结构在地震重现期为2450年水准的地震作用下，主梁梁端与索塔塔顶产生了很大的位移，分别达到了1.06 m和1.25 m。主梁梁端的大位移将造成结构碰撞，从而引起结构损伤，塔顶过大的位移也将增大P-△效应，从而增大索塔塔底的弯矩，使索塔结构的受力状态更为不利。当设置了阻尼器后，主桥纵桥向设置的粘滞性阻尼器有效地耗散结构在地震作用下的输入能量，主梁梁端与索塔塔顶的最大位移均下降至原来的20%～60%，当阻尼参数C一定时，主梁梁端与索塔塔顶位移均随阻尼指数α的减小而逐渐减小，当阻尼指数α一定时，梁端与塔顶的位移均随阻尼系数C的增大而逐渐减小，这表明，当阻尼系数C取大值，阻尼指数α取小值时，粘滞阻尼器能够更好地发挥耗散地震输入能量的能力，得到更好的减震效果。

图10、图11所示为不同阻尼器参数情况下索塔塔底弯矩、塔底剪力的变化规律。从图中可以看出：当设置了主桥纵桥向阻尼器后，索塔塔底弯矩均有了大幅度的下降。对于不同参数的粘滞阻尼器，索塔塔底弯矩减小至不设阻尼器工况下索塔塔底弯矩的30%～60%。与位移变化趋势相同，索塔塔底弯矩随阻尼指数α的减小而逐渐减小，随阻尼系数C的增大而逐渐减小，在阻尼系数为20 00～3 000范围内，塔底弯矩衰减较快，随后趋于平缓。索塔塔底剪力变化趋势与塔底弯矩的变化趋势相近，不同之处在于，与不设阻尼器的工况相比，设置不同参数的粘滞阻尼器后，索塔塔底剪力水平基本相当，差异仅仅在±10%以内。分析其原因在于：主桥纵向设置了粘滞阻尼器后，一方面使得地震作用下主梁的纵桥向水平惯性力主要传递途径由拉索→索塔→基础改变为粘滞阻尼器→索塔→基础，降低了惯性力的作用点，减小了惯性力对于基础的力臂，从而减小了结构基础承受的弯矩；另一方面，粘滞阻尼器的设置有效地减小索塔的地震位移响应，索塔内P-△效应减小，同样也减小了结构基础承受的弯矩。而索塔塔底剪力则主要由地震作用下结构的惯性力贡献。由于设置阻尼器后并不改变结构的振动周期，因此地震加速度响应变化并不十分显著，结构惯性力差异也不大，与不设阻尼器的情况相比，设置不同参数的阻尼器后索塔塔底剪力相差不大。

图12、图13所示为不同阻尼器参数情况下塔梁间纵向相对位移（阻尼器所需要的最大行程）和阻尼器阻尼力的变化规律，从图中可以看出：塔梁间相对位移随着阻尼器阻尼系数C的增大而减小，随阻尼指数α的减小而减小。而阻尼器阻尼力的变化规律则与之相反，随着阻尼参数的增大，阻尼力也逐渐增大，随阻尼指数α的增大而逐渐减小。

从阻尼器参数的分析可知，当阻尼系数C取大值，阻尼指数α取小值时，粘滞阻尼器能够更好地发挥耗散地震输入能量的能力，得到更好的减震效果。但这并不意味着在进行阻尼器参数的选择时即可简单使用这一原则。阻尼器参数的选择往往需要综合考虑各种因素进行。既需要使得阻尼器的设置能更为有效地耗散地震输入能量，又应控制结构位移，能与结构构造设计相适应，同时还降低使得阻尼器制作加工和安装难度。就阻尼指数α来说，当其数值越小时，阻尼器在结构振动速度较低时即能提供较大的阻尼力，其减震效果越好，故一般可采用较小值；阻尼系数C的增大则显著提高阻尼力的水平，阻尼力的增大一方面造成阻尼器质量体积增大，从而提高了阻尼器制作加工的要求和施工安装的难度，另一方面也提高了其与塔、梁连接部位的强度要求。故应结合结构位移控制要求，来确定阻尼系数C的取值。

该工程综合考虑梁端位移、阻尼器行程范围和最大阻尼力等各种因素。结合桥梁结构的特点，在每个索塔与主梁间设置4个纵向粘滞性阻尼器进行减震，全桥共设置8个阻尼器。每个阻尼器的参数选择为C=2 300 kN，阻尼指数采用α=0.2。设置了所选择的粘滞性阻尼器后，结构主要地震反应列于表2。结果表明阻尼器的设置使得塔底的弯矩、塔顶和梁端位移均降至40%，提高了结构的抗震性能。

表2 结构主要地震反应一览表

4 结论

通过对该越江大跨度混凝土斜拉桥粘滞性阻尼器的参数分析，可以得出以下结论：

（1）在主桥纵桥向设置粘滞性阻尼器，可以有效地耗散结构在地震作用下的输入能量，从而减小主桥索塔塔顶、主梁梁端及塔上支座处的纵向位移，从而可以避免或减轻碰撞引起的结构损伤。

（2）在该桥纵向设置粘滞性阻尼器，可以使得地震作用下主梁的纵桥向水平惯性力传递途径由拉索→索塔→基础改变为粘滞阻尼器→索塔→基础，降低了惯性力的作用点，减小了惯性力对于基础的力臂，从而减小了结构基础承受的弯矩。塔底剪力变化幅度不大。

（3）在不同参数的阻尼器情况下，塔底弯矩、塔梁相对位移的变化规律相似，即当阻尼指数一定时，随着阻尼系数的增大，塔底弯矩、塔梁相对位移均相应减小；当阻尼系数一定时，随着阻尼指数的增大，塔底弯矩、塔梁相对位移均相应增大。阻尼器阻尼力的变化规律则与之相反.

（4）阻尼器的选取应综合考虑梁端位移、阻尼器行程范围和最大阻尼力等各种因素。结合桥梁结构的特点，该桥粘滞阻尼器可设置8个，每个阻尼器的参数选择为C=2 300 kN，阻尼指数采用α=0.2。

[1]谢旭.桥梁结构地震响应分析与抗震设计[M].北京：人民交通出版社，2006.

[2]柳炳康，沈小璞.工程结构抗震设计[M].武汉：武汉理工大学出版社,2005.

[3]王志强，胡世德，范立础.东海大桥粘滞阻尼器参数研究[J].中国公路学报，2005，18（3）:37-42.

[4]韩万水，黄平明，兰燕.斜拉桥纵向设置粘滞阻尼器参数分析[J].地震工程与工程振动，2005，25（6）146-151.

[5]叶正强，李爱群，徐幼麟.工程结构粘滞流体阻尼器减震新技术及其应用[J].东南大学学报（自然科学版），2002，32（3）.

[6]Xu Y L，He Q，Ko J M.Dynamic response of damper-connected adjacent buildings under earthquake excitation[J].Engineering Structures，1999，（21）:135-148.