车辆荷载作用下钢管混凝土拱桥的动态分析
2015-01-08方宁
方宁
(上海浦东环保发展有限公司,上海市 200127)
0 引言
随着交通事业的发展,汽车的行驶速度不断提高,载重不断增加;与此同时,材料工业的不断发展、高强材料的普遍应用使得桥梁向轻型化发展,活载在总荷载中所占的比重不断增加。因此,公路桥梁的车振问题日益突出。但由于我国对公路桥梁车振研究总体上开展得较晚,所以钢管混凝土拱桥的车振问题的研究也开展得不够。
钢管混凝土拱桥中的中下承式拱桥基本上采用柔性吊杆连接拱肋与桥面系,除少数拱梁组合桥外,大部分桥梁的桥面系与拱肋是处于相互独立的结构。在振动计算结果中表现为两者的振动不同步;在使用中表现为车辆经过时桥面振动较大。因此,有必要对大跨度钢管混凝土拱桥由于汽车通过引起的动态响应进行研究。
1 车辆动荷载的分析计算
1.1 不平整路面的生成
由于道路表面具有不规则性,当车辆以一定速度驶过时,路面形状的不规则会给车辆一个激励,从而引起车辆的振动,结果导致连续变化的轮胎力,即轮胎力关于静力学值的波动(动力学轮胎力),并最终引起道路表面的动应力和动应变。因此,路面不平度是研究车辆动荷载的关键和前提。
路面不平整是引起车辆振动的主要原因,大量的测试和研究都已经表明,它是一个典型的随机过程。依据文献[1],本文把路面不平整度简化为正弦函数。
路面不平整度可表示为:

其中:y0是路面不平整的幅值;k=2π/λ,λ 表示路面不平整的波长;φ为初始相位,这里不妨取为零。根据 x=νt,并令 w=kν=2πν/λ,则式(1)可改写为式(2):
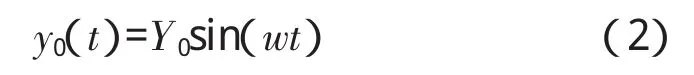
1.2 动荷载计算
车辆是一个多质点的复杂振动系统,因此要描述车辆的实际振动情况是一个相当复杂的问题。国内外已有的研究报告和实测资料指出:采用四分之一车身结构的两自由度车辆振动模型来测定车辆垂直振动的加速度时能达到令人满意的精度。图1为采用1/4车的两自由度模型。

图1 振动系统模型
在图1中,m1表示非悬挂质量(车轮质量);m2表示悬挂质量(车身质量);k1表示轮胎刚度;k2表示悬挂弹簧刚度;c1表示轮胎阻尼系数;c2表示悬挂阻尼器阻尼系数。
该两自由度系统受迫振动的运动微分方程为:

模型中有两个自由度,考虑了弹簧阻尼影响,理论计算繁琐。因此,利用大型通用有限元软件ANSYS进行求解,计算得到的结构支座反力即为车辆作用于路面的动荷载值。考虑自重影响,则动荷载值可表示为:

2 模型的建立
2.1 算例介绍
某桥主桥为3跨中承式钢管混凝土拱桥,最大跨径为120 m,矢跨比1/4,拱轴线为二次抛物线形。拱肋断面为哑铃形,截面为等高度、变钢管壁厚,其断面见图2所示。拱肋采用1 6 Mn钢板,钢管和腹板内浇注C40混凝土。吊杆和立柱间距为6 m;吊杆采用109根直径为5 mm碳素钢丝组成,钢丝的标准强度为1 600 MPa;立柱采用钢筋混凝土结构,混凝土为C25,立柱截面为80 cm×80 cm。

图2 钢管混凝土拱肋断面图
2.2 建立有限元模型
结构非线性问题通常分为两大类,即材料非线性问题和几何非线性问题。在施工过程和使用阶段的受力分析中,拱桥的非线性影响主要由几何非线性引起,材料非线性的影响一般可不考虑。因此,在分析中仅考虑几何非线性影响。钢管混凝土组合材料截面采用等效截面方法,按中国工程建设标准化协会标准《钢管混凝土结构设计与施工规程》(CECS28:90)等效计算,即:

在式(5)和式(6)中,EA 表示钢管混凝土压缩和拉伸刚度;EI表示钢管混凝土弯曲刚度;EC、ES表示混凝土和钢管的弹性模量;AC、AS表示混凝土和钢管的截面面积;IC、IS表示混凝土和钢管的惯性矩。据此,求得钢管混凝土拱肋的截面属性为:EA=5.04×1010(N);EI=1.88×1010(N·m2)。
本文主要研究车辆荷载对钢管混凝土拱平面内的动力响应问题,因此建立2-D平面模型。拱肋用非线性杆单元模拟;桥面和横梁系统简化为非线性杆单元;拉杆用只拉链杆单元模拟;立柱用只压链杆单元模拟,2-D模型见图3所示。

图3 钢管混凝土拱桥模型
2.3 车辆动荷载的实现
有限元方法是把连续体离散成多个单元进行分析,因此当车辆行驶到节点处时,车辆动荷载可直接施加到节点上;而当车辆行驶到两节点间的位置时,采用线性分配原则,把荷载分配施加到两个节点上。具体分配方法,见图4所示。假设某一时刻荷载 p(t)运动到如图所示位置,那么:p(i)=

图4 车载分配原则示意图
3 有限元计算及结果分析
本文采用文献[2]的载重车辆,车辆各参数:m1=500 kg,m2=4 500 kg,k1=2 000 000 N/m,k2=1 000 000 N/m,c1=8 000 Ns/m,c2=1 4000 Ns/m。取路面不平整的波长,路面不平整的幅值。考虑车速分别为 30 km/h、60 km/h、80 km/h、120 km/h的情况,车动荷载谱见图5所示。
从图5可见,车动荷载开始阶段变化幅度较大,然后趋于平稳,这是由于体系自振作用和阻尼作用的原因。
动力荷载作用与桥梁结构上产生的动挠度,一般较同样的静荷载所产生的相应的静挠度要大。动挠度与相应的静挠度的比值称为活荷载的冲击系数。由于挠度反映了桥梁结构的整体变形,是衡量结构刚度的主要指标,因此活载冲击系数综合地反映了动力荷载对桥梁结构的动力作用。一般规定冲击系数为:车辆驶过桥梁时,观测跨中截面地挠度时程曲线,以此得到车动荷载的冲击系数。但对于无铰拱等结构体系,当车辆驶过桥梁时,车动荷载引起的跨中挠度有可能向上,这对于大跨拱桥是有利的。因此,本文考虑车辆过桥时,取其时间点上的最大向下位移进行分析,以此得出冲击系数。冲击系数定义为:

其中:Ydmax表示最大动挠度值;Y smax表示最大静挠度值。
利用有限元分析软件opensees,计算出不同车速情况下的最大挠度(见图6)。
从不同车速的最大挠度响应图(图6),可见以下特点:
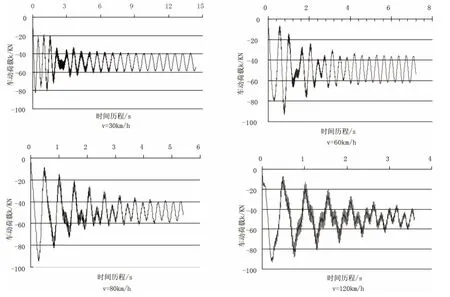
图5 车辆动荷载谱

图6 最大挠度响应图
(1)在四种车速情况下,最大挠度响应均发生在1/4拱肋处。说明车辆动荷载作用下,中承式钢管混凝土拱桥的动挠度控制截面为1/4拱肋位置。
(2)拱桥的前半跨动挠度响应值较后半跨值大。参照车辆动荷载谱图(图5),可见开始阶段的车辆动荷载幅值较大。这是因为开始阶段阻尼影响不明显,车动荷载谱需要一定时间才能基本达到稳定振动。因此,振动开始计算点的选取对拱桥挠度响应影响较大,在实际运用中必须计算不同振动开始点的挠度响应,取最不利结果。另外,车辆加速行驶和车辆紧急制动都会对拱桥动挠度响应产生很大影响,这是因为加速行驶和制动都引起结构体系的不稳定振动。
(3)冲击系数并不总是随着速度的增大而增大,从冲击系数表(见表1)中可知:速度ν=60 km/h的冲击系数比速度ν=30 km/h时大,两者相差23.8%;但随着速度的增加,速度ν=80 km/h时的冲击系数反而比ν=60 km/h时稍小,两者相差7.9%;当速度ν=120 km/h时,冲击系数最大,比ν=60 km/h时冲击系数大11.9%。从冲击系数变化图(见图7)中可清晰看出冲击系数随速度变化的趋势。
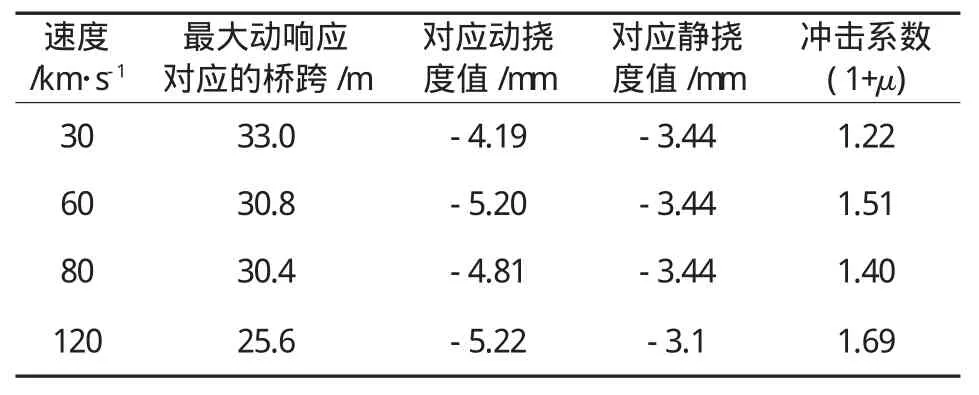
表1 不同速度对应的冲击系数表

图7 冲击系数随速度变化曲线图
4 结论与展望
(1)中承式钢管混凝土拱桥在车辆动荷载作用下,其挠度最大响应位置为1/4拱肋处。
(2)计算开始点的选取对钢管混凝土拱桥挠度响应的影响非常大,因此实际运用中应该准确确定开始计算点的位置。对于不能准确确定开始计算点的情况,需要计算所有不利点位置,取其中最大值作为设计依据。
(3)整体上,冲击系数随速度的增大而增大,但冲击系数-速度曲线并不是单调递增,在某个速度段存在减小的趋势。
(4)车辆制动及加速行驶都会影响钢管混凝土拱桥的动力响应,但本文限于篇幅没做分析。另外,路面不平整是一个随机过程,把不平整作为正弦规律考虑不能完全反映实际情况。
[1]周华飞,蒋建群,毛根海.路面不平整引起的车辆动荷载分析[J].中国市政工程,2002,3(25):10-13.
[2]徐建平,尚刚,梁乃兴.路面不平整引起的汽车动荷载计算分析[J].重庆交通学院学报,2001,20(1):26-28.
