基于极化的浅埋目标体时域瞬态响应处理方法

朱彦龙,欧阳缮

(桂林电子科技大学信息与通信学院,广西桂林 541004)

基于极化的浅埋目标体时域瞬态响应处理方法

朱彦龙,欧阳缮

(桂林电子科技大学信息与通信学院,广西桂林 541004)

为了获取瞬态响应蕴含的目标特征信息,提出一种基于极化的时域瞬态响应的处理方法。以早时响应中表面反射波能量相等为基础,计算加窗后各个数据窗下的最大奇异值,确定最大奇异值下降速率骤降时刻为晚时响应阶段的开始点。仿真结果表明,本方法能够实现对早时响应与晚时响应的分离。

探地雷达;早时响应;晚时响应;极化;奇异值

探地雷达(ground penetrating radar,简称GPR)是一种利用地下介质的非连续性探测地下目标的有效方法,由于具有探测范围广、探测过程连续、操作方便、非破坏性等优点,被广泛应用于公路铁路、桥梁隧道、国防公安、考古考察等诸多领域[1]。GPR采用脉冲宽度极窄的高斯脉冲信号作为入射信号照射目标体,接收后向散射信号获取目标的时域瞬态响应。

根据奇点展开法(singularity expansion method,简称SEM)理论,目标的时域瞬态响应可分为早时响应与晚时响应[2]。早时响应是由入射信号到达目标体并开始与目标作用,直到入射信号完全与目标相互作用而产生的响应信号,包含不同散射中心的光学散射以及绕行目标体产生的调制信号。晚时响应是入射信号完全通过目标体后,目标体自身保留了因入射信号产生的感应电流而向外辐射的信号。其中,感应电流与目标体的自然共振频率有关,且可表示为一系列阻尼振荡函数的叠加[3]。研究目标瞬态响应中早时响应和晚时响应的处理方法,可分析早时响应与晚时响应中蕴含的目标体信息。

对于瞬态早时响应与晚时响应处理方法的研究, Felsen等[4]以圆柱体为例,从理论上阐述了瞬态响应的组成,以绕射波等为表现形式的早时响应和以共振态为表现形式的晚时响应。在此基础上,Ilavarasan等[5]具体阐释了晚时响应的开始点,前提是必须具备目标体的先验知识,而在实际应用中,具备目标体的先验知识并不现实。文献[6]用时域解卷积对半空间介电目标冲激响应进行建模,分析了包含目标特殊信息的晚时响应提取方法。文献[7]采用矩量法计算目标的频域散射数据,经逆傅里叶变换及运用相应的信号处理手段,得到多个方位的目标晚时响应数据。文献[8]通过设置连续的时间窗,估计出每个时间窗下对应晚时响应的一组极点,利用极点的收敛性反推出自由空间下圆柱体早时响应与晚时响应的分界点,但关于计算过程中如何确定起始点的选择、窗的大小及步长,并没有给出合理的解释。伴随着电磁场领域的飞速发展,极化的应用非常普遍[9-10]。文献[11]通过测量感兴趣目标早时和晚时极化特性,用极化差异来抑制早时响应,可优化早时响应抑制性能,但要求晚时极化特性与早时极化特性有明显差异。文献[12]通过理论推导,利用不同的极化信息,成功分离出了细长圆柱体的早时响应与晚时响应,方法简便,但仅限于自由空间。

对于介质环境下的目标体,早时响应与晚时响应的处理方法研究较少。为此,在不同极化下早时响应中表面反射波能量相等的基础上,提出一种处理浅埋目标体时域瞬态响应的方法。利用加窗后的数据构造的Hankel矩阵最大奇异值与瞬态响应的时间进程关系,将最大奇异值骤降的时刻定义为晚时响应的开始点。

1 瞬态早时响应与晚时响应的理论分析

1.1 早时响应的极化分析

探地雷达利用发射天线向地下发射高频宽带电磁波,电磁波在地下介质传播过程中,当遇到电性差异的目标时,会发生反射、折射等现象,接收天线接收后向散射信号,获取目标的时域瞬态响应。探地雷达包括雷达收发天线、有耗媒质、目标(细长圆柱体),其系统模型如图1所示。

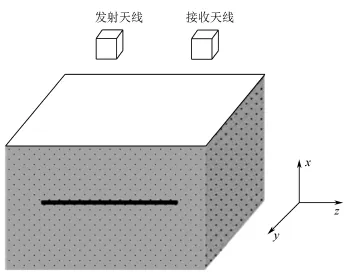
图1 探地雷达系统模型Fig.1 The model of GPR

根据发射天线发射的电磁波中电场强度的方向不同,电磁波可分为不同的极化方式。在球坐标系中,当电场方向与俯仰角θ变化的方向相同时,称为θ极化;当电场方向与方位角φ变化的方向相同时,称为φ极化。2种情况下,目标体产生的时域瞬态响应可表示为:

其中:等式右边第一项为早时响应,Epbos(t)由目标的初期散射分量、物理光学散射等组成,集中了瞬态响应的大部分能量和高频部分;等式右边第二项为晚时响应,表现为一系列阻尼振荡函数的叠加;sn=σn+ j2πfn为目标体的自然共振频率,σn、fn分别为衰减因子和谐振频率;u(t)为阶跃函数;tL为早时响应与晚时响应的理论分界点。

选择如图1所示的直角坐标系,假设发射天线垂直入射目标体,选取远场处接收目标体的后向散射信号。入射波采用单位幅度的高斯脉冲,θ极化下,电场的方向沿―z方向,磁场的方向沿―y方向;φ极化下,电场的方向沿y方向,磁场的方向沿―z方向。θ极化下入射波表示为:

φ极化下入射波表示为:

坡印廷矢量又称能量密度矢量,其方向表示能量的流动方向,大小表示单位时间内穿过与能量流动方向垂直的单位面积能量。由于在远场处接收后向散射信号,θ极化与φ极化下,目标的早时响应中表面反射波的平均坡印廷矢量分别为:

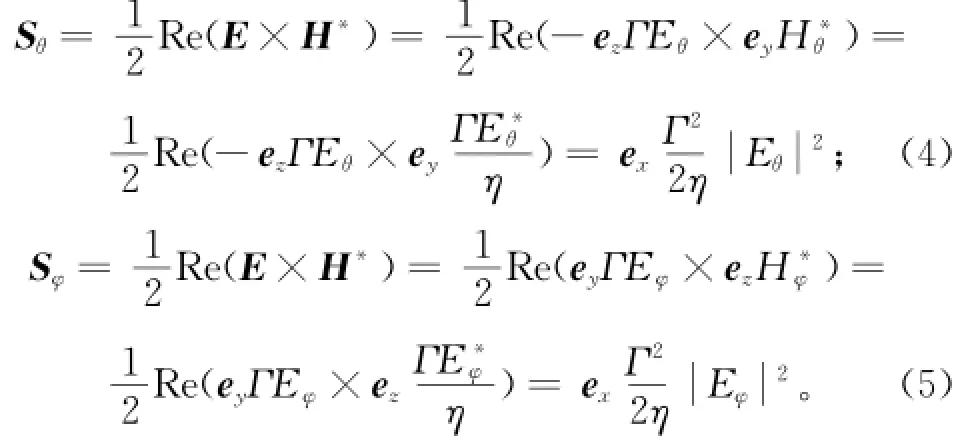
其中:Γ为反射波电场振幅与入射波电场振幅的比值,记为反射系数;η为自由空间下的波阻抗。由式(2)、(3)可知,Eθ=Eφ,因此,2种极化方式下,目标早时响应过程中的表面反射波的能量是相同的。

1.2 晚时响应的收敛特性分析

式(1)在拉普拉斯变换域可表示为:其中,早时响应的拉普拉斯变换是一个整函数,晚时响应的拉普拉斯变换则是关于极点的级数展开。极点的分布仅决定于散射体的外部特性(形状、大小、目标属性),而与入射波的大小及散射方向无关,即目标姿态的改变并不影响极点的分布特征。基于SEM理论的时域回波模型对时域瞬态响应的晚时部分,为了更精确地估计出晚时响应的开始时刻,必须选择一个时间维度上尽量靠前的点。在早时响应表面反射波能量相等的基础上,确定加窗处理的起始点,对起始点之后的时域瞬态响应数据进行时间窗取样,根据加窗后的数据构造的Hankel矩阵,求出每个矩阵的奇异值后,选取每个窗下的最大奇异值进行比较,确定最大奇异值骤降的时刻,即为晚时响应的开始时刻。

由早时响应与晚时响应的定义知,对于自由空间中的单一目标体,其时域瞬态响应的早时与晚时具有确定的分界点,而介质环境下的目标体,其时域瞬态响应的早时响应与晚时响应则会发生时间上的混叠。由于目标体与介质环境位置的相对关系,浅埋的目标体先于所在的介质体发生晚时响应,也可理解为:当外部介质体还处在发生反射、折射、绕射阶段时,浅埋目标体的晚时响应已开始。因此,图1所示的系统模型的时域瞬态响应,按时间先后可划分为3个阶段:早时响应阶段;早晚时混叠阶段;晚时响应阶段。利用θ极化与φ极化下早时响应表面反射波能量相等原理,可确定早时响应表面反射波结束的时刻,同时也可确定目标体的位置信息;利用最大奇异值与晚时响应的对应关系,可确定晚时响应阶段的开始点。

2 仿真结果分析

根据图1所示的系统模型,采用基于时域有限差分算法的电磁仿真软件XFDTD进行建模仿真分析。仿真环境中,入射波采用超宽带高斯脉冲源,脉冲半宽为1 ns,频带宽度约1 GHz。假设介质环境为干沙,其长a、宽b、高c分别为0.8 m、0.8 m、0.4 m,相对介电常数设为4,电导率为0.001 S/m。目标体以高导性质的细长圆柱体为例,埋深h为0.05 m,长度l设为0.7 m,半径r为0.005 m,保证r/l足够小,使得圆柱体更易发生明显的晚时响应。入射方向沿―x方向,φ极化与θ极化下模型的时域瞬态响应如图2、3所示。

由图2、3可知,2种极化下发生表面反射波的时刻相等,约为8.61 ns。由于在θ和φ两种极化情况下,细长圆柱体产生的后向回波信号不同,导致9.18 ns时刻处不同极化下的时域瞬态响应区别很大,以此可确定目标体所在的位置。随着时间的推移,入射波穿透介质环境发生反射(13.27 ns处)及沿表面发生绕射(18.29 ns处),2种极化下的瞬态响应均出现了类脉冲波形。考虑到仿真软件的计算速度,假设的系统模型中,介质环境以长方体代替,使得沿表面发生的绕射数目增多,因此,在13.27 ns后的一段时间内,目标的瞬态响应依然显示一定的类脉冲特性。

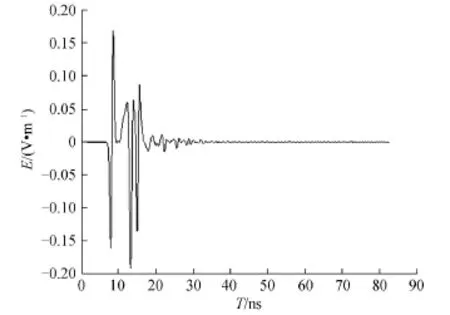
图2 φ极化下时域瞬态响应Fig.2 The transient response ofφ

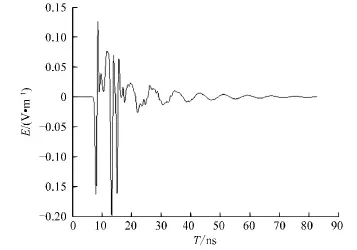
图3 θ极化下时域瞬态响应Fig.3 The transient response ofθ

对获取的时域瞬态响应采取分段处理,并对分段后的回波信号作短时傅里叶变换,能有效跟踪频谱能量随时间变化的情况。选取相邻信号段之间的叠加长度为每段长度的1/2,根据仿真条件可知,2种极化下接收的时域瞬态响应的时长均为82 ns,采样点数为3600个,采样间隔约为0.023 ns。选取每段信号的长度为100个点,相应的段数为71。计算每段信号的频谱能量并作归一化处理,其结果如图4所示。从图4可见,在9.18 ns时刻后,2种极化的能量有了显著区别,以此作为早时响应阶段表面反射波的结束点。

图4 不同极化下频谱归一化能量对比Fig.4 The comparison of normalization power with different polarization

采用θ极化方式时,模型的晚时响应更加明显,因此对θ极化下的回波信号进行分析。信号的长度选为400个采样点,约10 ns,以保证至少包含共振频率的一段信息。根据入射脉冲的脉冲宽度,选取50个采样点作为步长,约为1 ns。从早时响应中表面反射波结束的时刻(9.18 ns)开始,按照所取窗、步长的大小依次获得30组信号数据,求出每一组数据的最大奇异值,分析结果如图5所示。由图5可知,随着时间的推进,所求的最大奇异值逐渐减小,16.07 ns处为最大奇异值下降速率骤降的时刻,从而将此刻作为晚时响应阶段的开始点。

图5 各个窗下最大奇异值变化图Fig.5 The biggest singular value in different windows

当入射波到达目标体所在位置时,表面反射波结束。细长圆柱体早时响应的结束时刻,以入射波绕行圆柱体轴向长度的结束时刻为准,此后与外部介质环境的绕射发生混叠。晚时响应的开始时刻,以入射波绕行介质体的结束时刻为准,仿真值与理论值基本一致。

3 结束语

针对介质环境下目标体的早时响应与晚时响应的分离问题,分析了它们之间的关系,从不同极化下能量相等及奇异值特性2个角度出发,提出一种处理早时响应、晚时响应的方法。该方法简单高效,能有效确定目标体的位置,精确地分离出晚时响应,有助于实现介质特性反演及目标体方位识别。后续研究考虑将该法推广到更加符合实际的介质性质的目标体,例如对地下充水性质裂缝的探测等。

[1] 李巍.基于ANN的探地雷达浅层目标识别与电性能参数的反演[D].南昌:南昌大学,2012:1-2.

[2] Baum C E.The Singularity Expansion Method[M].Berlin,German:Springer-Verlag,197:129-179.

[3] Hutchinson S,Fernando M,Andrews D,et al.Investigation of late time response analysis for detection of multiple concealed objects[C]//Proceedings of SPIE Security +Defence International Society for Optics and Photonics,2013:88970O-13.

[4] Heyman E,Felsen L B.Creeping waves and resonances in transient scattering by smooth convex objects[J].IEEE Transactions on Antennas and Propagation,1983,31(3): 426-437.

[5] Li Q,Ilavarasan P,Ross J E,et al.Radar target identification using a combined early-time/late-time E-pulse technique[J].IEEE Transactions on Antennas and Propagation,1998,46:1272-1278.

[6] Padhi S K,Shuley N V.Resonance behavior of a dielectric target in a half-space using the CNR method[C]// IEEE Antennas and Propagation Society International Symposium,2006:715-718.

[7] 杨松岩.高频波段雷达目标特征提取[D].哈尔滨:哈尔滨工业大学,2009:31-37.

[8] Hong S K,Wall W S,Andreadis T D,et al.A practical implications of pole series convergence and the earlytime in transient backscatter[R].Washington:Naval Research Labor,2012.

[9] 冯晅,邹立龙,刘财,等.全极化探地雷达正演模拟[J].地球物理学报,2011,54(2):349-357.

[10] 郭士礼,蔡建超,张学强,等.探地雷达检测桥梁隐蔽隐蔽病害方法研究[J].地球物理学进展,2012,27(4): 1812-1821.

[11] Baum C E.Polarimetric suppression of early-time scattering for late-time target identification[C]//Ultra-Wide-Band and Ultra-Short Impulse Signals,2010:12-15.

[12] Zhou Lijun,Ouyang Shan,Jin Liangnian.Extracting turn-on time for analyzing transient scattered response of wire structures[C]//Signal and Imformation Processing,2013:49-53.

编辑:黎仁惠

A processing approach of time transient response for buried target based on polarization

Zhu Yanlong,Ouyang Shan
(School of Information and Communication Engineering,Guilin University of Electronic Technology,Guilin 541004,China)

To obtain the target feature information included by the time transient response,a new processing approach based on polarization is proposed.This method proves that the energy of surface reflection at different polarization is equal in earlytime response stage.With computing the biggest singular of each window,the break time of the singular value is the beginning of the late-time response stage.The simulation results show that the proposed approach can separate the late-time response effectively.

ground penetrating radar;early-time response;late-time response;polarization;singular value

TN957;P631

:A

:1673-808X(2015)04-0280-04

2015-03-18

国家自然科学基金(61371186);广西自然科学基金(2013GXNSFFA019004,2013GXNSFAA019329)

欧阳缮(1960―),男,江西安福人,教授,博士,研究方向为通信和雷达信号处理、自适应滤波理论和应用。E-mail:hmoysh@guet.edu.cn

朱彦龙,欧阳缮.基于极化的浅埋目标体时域瞬态响应处理方法[J].桂林电子科技大学学报,2015,35(4):280-283.