一种双曲抛物面上样条曲线的等距曲线算法

田 良,彭丰富

(桂林电子科技大学数学与计算科学学院,广西桂林 541004)

一种双曲抛物面上样条曲线的等距曲线算法

田 良,彭丰富

(桂林电子科技大学数学与计算科学学院,广西桂林 541004)

为了得到双曲抛物面上的等距曲线,提出一种双曲抛物面上样条曲线的等距曲线算法。在重心坐标系下,通过求双曲抛物样条曲线的法向量,得到相应的等距曲线。借助仿射变换和向量叉积,计算样条曲线的法向量。通过Matlab软件实现对等距曲线的绘制,并在给定节点的情况下对等距线进行拼接。结果表明,用该算法获取的双曲抛物面上样条曲线的等距曲线简单、快捷。

双曲抛物面;等距曲线;代数样条

等距曲线是基曲线上的每个点沿法方向移动距离为d的点的轨迹,为近十年来CAGD的一大热点。等距曲线在工业中应用十分广泛,其应用领域遍及公路、铁路线型设计,机器人行走路径规划,等间距挖洞加工,实体造型和图形学等[1]。

等距曲线逼近算法主要有5种[2]:1)等距移动控制网格得到等距曲线逼近曲线控制网格的方法;2)基圆包络法;3)基于插值拟合法;4)不会产生自交的逼近法;5)利用测地线得到等距曲线的方法。PH(Pythagorean hodograph)曲线为一类参数曲线,其表示平面多项式曲线的等距曲线表达式中分母根号内为完全平方,使得等距曲线可精确有理表示。PH条件是具有有理等距曲线的平面多项式曲线所应满足的一个充分条件。弗尔谢克和拉维斯卡[3-4]分析了代数曲线等距线的还原性,提出了一种类似PH条件的参数化曲线。文献[5]根据有理单位切向量提出了一种构建空间有理PH曲线的方法。张若楠等[6]利用改进的有理德卡斯特里奥算法求得一类正则有理贝齐尔曲线各点的切向量,得到各点单位法向量。文献[7-8]在重心坐标系下用双参数化方法生成双曲抛物面上样条曲线。为此,提出一种双曲抛物面上样条曲线的等距曲线算法,通过仿射变换和叉积运算得到样条曲线的单位法向量,进而得到样条的等距曲线,在给定节点的情况下,可以对等距曲线进行拼接,且拼接是G1连续的。

1 双曲抛物面样条曲线

文献[8]中,在笛卡尔坐标系中顶点为(0,0,0)、(1,0,0)、(0,1,0)和(0,0,1)的正四面体T*上定义一双曲抛物面,

式(1)通过u、v二个参数进行参数化[8-9],参数u、v关系由一个函数簇决定:

曲线可表示为:

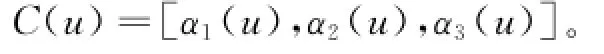
曲面(1)的法向量为:

则曲线C(u)的法向量为:

设P1,P2,P3,P4∈R3是非共面点,以P1、P2、P3、P4为顶点的非退化四面体(或三维单形)T=[P1P2P3P4],Pi=(xi,yi,zi)T。根据重心坐标系变换, T与T*的关系为:

J是α关于x、y、z的Jacobian矩阵:

正则样条曲线C(u)通过线性运算(4)构造非共面控制四边形上的样条曲线S(u)。S(u)的法向量为:

P1点的法向量nT(P1)是由P1、P2、P4组成平面的法向量,P4点的法向量nT(P4)是由P1、P3、P4组成平面的法向量,因此,曲面的法向量也是样条曲线的法向量。图1为控制四边形上样条曲线的单位法向量。

图1 样条曲线的单位法向量Fig.1 The normal vector of spline curve

2 构造等距曲线

定义给定一空间参数曲线S(u)=(x(u),y (u),z(u)),其距离为d的等距曲线Sd(u)定义为:其中n(u)为曲线S(u)的单位法向量。

正四面体T*由式(2)生成样条曲线C(u),且有法向量n(u),根据等距距离d,可得该样条曲线的等距曲线如图2所示。

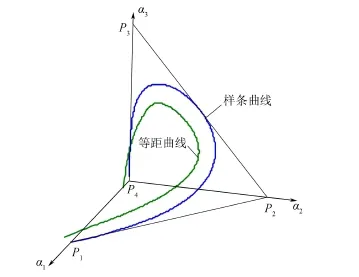
图2 正四面体上的样条曲线和等距曲线Fig.2 Spline curve and its offset in a regular tetrahedron

样条曲线C(u)经仿射变换式(4)可映射到任意四面体,但样条曲线C(u)的法向量经式(4)的变换后得到的向量nT(u)不一定是样条曲线S(u)的法向量。因此,给出一个准确的样条曲线S(u)的法向量的计算方法。

设样条曲线Si(u)上Pi点的切向量为m(Pi), nT(Pi)是通过式(5)的变换得到的向量,则Si(u)的法向量可表示为:

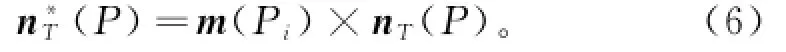
对任意给定控制四边形的样条曲线,都可通过式(6)获得其法向量及相应的等距曲线(见图3),四边形退化为平行四边形同样可以实现。

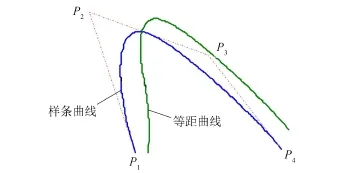
图3 四面体上的样条曲线和等距曲线Fig.3 Spline curve and its offset in a tetrahedron

3 样条曲线的等距曲线的拼接

双曲抛物面上的样条曲线可进行拼接[8-9],等距曲线是样条曲线由法向量移动一段距离得到,同样也可在一定条件下进行拼接。

定理2个顶点分别为P1、P2、P3、P4和P1*、P2*、P3*、P4*的四面体H和H*,对双曲抛物面进行双参数化[8],分别生成样条曲线S1(u)和S2(u),设它们的等距曲线为Cos(1)和Co(2s)。

1)在P2、P3、P4、P4*、P2*五点共面的条件下,等距曲线Co(1s)和Co(2s)尾尾相连(在P4和P4*点拼接)后是G1连续的。

2)在P2、P4、P1*、P3*、P4*五点共面的条件下,等距曲线Co(1s)和Co(2s)首尾相连(在P4和P1*点拼接)后是G1连续的。

证明根据文献[8],正四面体中P1的坐标为(α1,α2,α3)=(1,0,0),代入

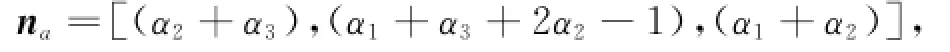
得n(P1)=(0,0,1)。正四面体中P1点的法向量经过式(5)变换得到的向量为:

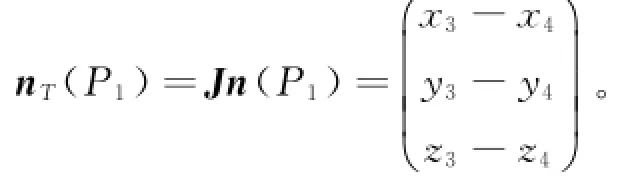
由此可知,正四面体端点P1的法向量变换后的向量nT(P1)方向平行于P3P4。同理可得端点P4的法向量变换后的向量nT(P4)平行于P2P4。

1)等距曲线在P4和P4*点拼接。若P2、P3、P4、P4*、P2*五点共面,则经过式(5)变换得到的向量nT(P4)与nT(P4*)共面,

由此可得n*T(P4)//n*T(P*4),即在点P4和P*4有一致的法方向,等距曲线可拼接且是G1连续的。2)等距曲线在P4和P*1点拼接。若P2、P4、P*1、P*3、P*4五点共面,则经过式(5)变换得到的向量nT(P4)与nT(P*1)共面,

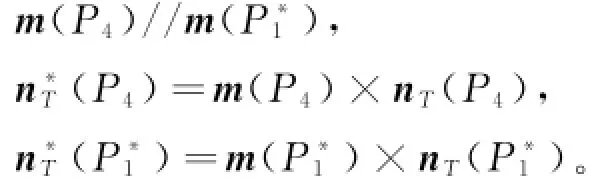
由此可得n*T(P4)//n*T(P1),即在点P4和P*1有一致的法方向,等距曲线可拼接且是G1连续的。定理得证。

图4、5是等距曲线尾尾相连和首尾相连拼接的例子。

图4 等距曲线尾尾相连拼接Fig.4 Offset curve attached in tail and tail

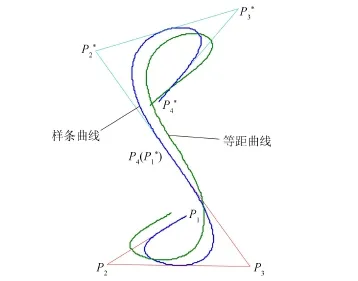
图5 等距曲线首尾相连拼接Fig.5 Offset curve attached in fore and aft

4 构造等距曲线的算法

给定空间节点的等距曲线的算法如下:

1)输入控制顶点{Pi}(i=1,2,…,n),等距距离d,初始条件i=1,f=0。

2)若n＜4,退出算法。假设P1(i)=Pi,P2(i)=Pi+t(Pi+1―Pi―1),P2(1)可作为一个预留点,P3(i)= Pi+1+t(Pi+2―Pi),P3(n―1)可作为一个预留点,P4(i) =Pi+1。若四点共面,则生成平面样条曲线;若四点不共面,则生成空间样条曲线。

3)在给定的空间四面体内构造样条曲线S(i)(u),方法参考文献[8]。

4)S(i)(u)的单位法向量可用式(6)求得。若P 2(i―1)和P3(i)在由点P1(i)、P 2(i)和P4(i)所在平面π的同一边,令f=f+1。

5)得到等距线Cos(i)=S(i)(u)+(―1)fnTi(u)。

6)若i=n―1,算法结束,否则i=i+1,转步骤2)。为了实现拼接,取适当的t,使得P(i)、P(i)、24 P 1(i+1)、P3(i+1)、P4(i+1)或者P2(i)、P 3 (i)、P 4 (i)、P 1 (i+1)、P 3(i+1)五点共面。

5 结束语

与传统的等距曲线构造相比,利用仿射变换直接求取样条曲线的法向量十分方便,不需要对原曲线进行逼近计算。在Matlab中可使用该方法进行编程,绘制等距曲线并进行拼接。但是本算法未对此构造方法产生的等距曲线的精度进行深入的研究,也未说明其中存在的误差,是一个处于初级阶段的新理论,今后需要在实验过程中加入一些附加条件,提高其精度。

[1] Pottmann H.Rational curves and surfaces with rational offsets[J].Computer Aided Geometric Design,1995 (12):175-192.

[2] Mackawa T.An overview of offset curves and surfaces [J].Computer Aided Design,1999,31(3):165-173.

[3] Vrsek J,Lávicka M.Reducibility of offset to algebraic curves[J].Computer Aided Geometric Design,2013,30 (1):140-147.

[4] Vrsek J,Lávicka M.Exploring hypersurfaces with offset-like convolutions[J].Computer Aided Geometric Design,2012,29(9):679-690.

[5] Farouki R T,Sakkalis T.Rational pythagorean-hodograph space curves[J].Computer Aided Geometric Design,2011,28(2):75-88.

[6] 张若楠,黄有度.一类有理Bézier曲线的等距线算法及MATLAB实现[J].大学数学,2012(2):59-63.

[7] Peng Fengfu,Han Xuli.Parametric spline on a hyperbolic paraboloid[J].Journal of Computional and Applied Mathematics,2009,229(1):183-191.

[8] Peng Fengfu,Chen Juanjuan.Spline on a generalized hyperbolic paraboloid[J].Journal of Computional and Applied Mathematics,2011,235(8):2451-2458.

编辑:翁史振

An offset algorithm of spline on hyperbolic paraboloid

Tian Liang,Peng Fengfu
(School of Mathematics and Computational Science,Guilin University of Electronic Technology,Guilin 541004,China)

In order to obtain the spatial offset curve for a spline in the hyperbolic paraboloid,an offset algorithm of spline on hyperbolic parabolid is presented.The principal normal vector of the hyperbolic paraboloid spline is solved to get its offset curve with its barycentric coordinate systerm.With the help of affine transformation and vector cross product,the normal vector of spline curve is calculated.Through Matlab software,the equidistant curve drawing is implemented,and the equidistant line is spliced in the case of a given node.The results show that the method is fast and convenient in drawing offset curve of spline on hyperbolic paraboloid.

hyperbolic paraboloid;offset curve;algebraic spline

TP391.7

:A

:1673-808X(2015)04-0336-04

2015-03-13

国家自然科学基金(11361018)

彭丰富(1972―),男,湖南娄底人,副教授,博士,研究方向为计算机辅助几何设计和数值计算。E-malil:28761025@qq.com

田良,彭丰富.一种双曲抛物面上样条曲线的等距曲线算法[J].桂林电子科技大学学报,2015,35(4):336-339.