基于稀疏测度PSF估计的天文图像复原改进算法

邵云龙

(桂林电子科技大学信息与通信学院,广西桂林 541004)

基于稀疏测度PSF估计的天文图像复原改进算法

邵云龙

(桂林电子科技大学信息与通信学院,广西桂林 541004)

为了解决地基天文观测中由大气湍流造成的图像模糊问题,利用基于稀疏测度的PSF估计算法实现PSF准确信息的重构,提出一种变正则化参数的改进的稀疏测度PSF估计算法,通过选择合理的参数,提高了PSF估计精度。实验结果表明,改进后的算法能更准确地估计PSF,提高图像复原的效果。

地基天文;大气湍流;稀疏测度

在地基天文中,通过光学望远镜观测天文目标时必须穿过厚厚的大气层这一非均匀介质,使得观测图像因受到大气湍流的影响出现严重的模糊[1]。观测图像中目标变得模糊不清、天体相对位置发生偏移等,使得对观测图像的分析识别变得困难重重,因此,需要对天文观测图像进行复原。受到噪声的干扰,图像复原本身具有病态性,而点扩散函数(point spread function,简称PSF)准确信息的缺失使得问题的病态性加重。

模糊图像的PSF估计是当前图像复原领域研究的热点。现已有很多模糊图像PSF的估计方法,总体上分为2类:

1)利用图像的边缘估计PSF[2-4],这类算法估计图像的边缘,并用模拟的块替换模糊图像的边缘,由此估计出PSF。由于现实模糊图像中需要被替换的复杂纹理信息往往遭到严重的破坏,此类算法不稳定,甚至产生错误的PSF。

2)充分利用自然图像统计信息的先验知识,即它们的分布导数和PSF是稀疏的、连续的。利用这些信息,此类算法通过最大后验概率方法[5-6]或者简单的代价函数[7-8]来估计PSF。

与一般图像相比,大多数天文观测图像没有明显的边缘,因此,基于边缘信息估计PSF的算法往往达不到理想的效果,且天文图像本身具有稀疏的特性,更易于稀疏表达。文献[7]提出一种基于稀疏测度的图像PSF估计算法,经天文背景下仿真分析对比,该算法能较为精确地重构天文图像PSF准确信息,适用于天文图像的PSF估计。

为此,基于稀疏测度的PSF估计算法[7],结合反映图像噪声水平的指数度量,通过在天文背景下大量仿真,提出一种变正则化参数改进的PSF估计算法,其基本思路是根据观测图像的噪声水平自适应调整正则化参数,提高PSF估计精度。

1 稀疏测度正则项l1/l2

图像复原问题本身具有病态性,使得图像复原的解不唯一或PSF信息的少许变化就会使解出现极大的波动。通过对解进行正则化约束是解决图像复原病态问题的常用方法[9-10]。

首先考虑l1范数。l1范数能很好地表达信号的稀疏性,l0范数在这一方面更加优秀,但是l0范数在实际求解时缺乏有效的数学工具。而l1范数可逼近l0范数的系数表达的效果,且通过数学工具易于求解,因此广泛应用于图像或信号的稀疏表达。但单纯的l1范数具有尺度可变性,对一幅图像来说,简单减小图像维度就可使其变小。图像处理中,l1范数通常用于图像的高频带。但噪声也通常位于图像的高频处,当噪声污染严重时,该区域的l1范数值随之增大,此时若最小化l1范数值,可达到抑制图像中噪声的效果。在图像模糊时,情况恰恰相反,最小化l1范数值在抑制图像高频噪声的同时也使得图像高频分量逐渐丢失,导致图像的模糊,这对图像去模糊显然是不利的。

l1/l2函数是l1范数的标准化,使l1范数具有尺度不变性。当图像模糊时,由于高频分量的衰减使得l1范数和l2范数的值同时减小,但是后者减小更快,总体上两者的比值增大,如图1所示。从图1可看出,尺度不变的正则项l1/l2能正确反映图像模糊的变化,最小化图像中高频部分的l1/l2值是一种有效的去模糊的方式。

对于一幅图像I,用不同大小(1～10)的高斯模糊算子b对其进行模糊处理,并计算成本

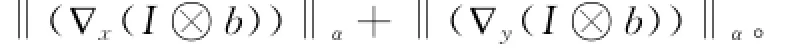
其中:∇x、∇y为相应的关于x、y的偏导数;α为范数类型,取0.5、1、2。纵坐标轴为不同模糊程度下成本值与原始成本值的比。

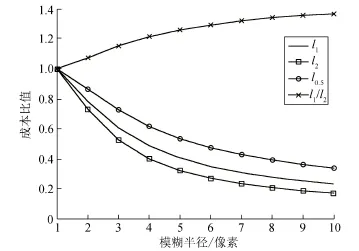
图1 不同正则项对比示意图Fig.1 The comparison of different image regularizers

2 基于变正则化参数的改进PSF估计算法

图像的中低频带包含了图像中的绝大部分能量,由于模糊导致图像中的高频分量减小,对图像的中低频不敏感。在模糊过程中,图像的高频分量衰减比较严重,此时,对应的l1/l2范数变化比较大,因此, l1/l2范数必须作用于图像的高频部分。

对于一幅含有噪声的模糊图像g,通过与滤波器∇x=[1,―1]和∇y=[1,―1]T卷积得到图像的高频部分y=[∇xg,∇yg]。其代价函数[14]为:

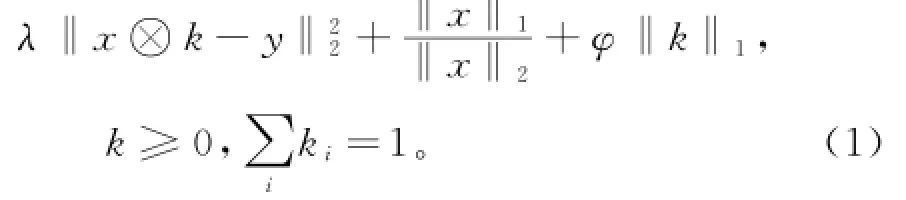
其中:x为未知的清晰图像的高频部分;k为未知的模糊核;⊗为二维卷积操作符。式(1)包含3项:第1项为保真项;第2项为关于x的正则化项;第3项为关于PSF的正则化,目的是减小PSF中的噪声。

在基于正则化方法的图像复原算法中,正则化参数的选择需要同时考虑复原结果的稳定性和与真实解的逼近性,并在这两者之间做出很好的平衡。若正则化参数取得过大,算法的解会过度地向正则化项倾斜,偏离真实解;若正则化参数选取过小,算法的解倾向于逼近真实解,但由于正则化项作用过小,使得无法有效解决问题的病态性,降低了解的稳定性。因此,当观测图像中噪声水平高时,问题的病态性比较严重,需要增大正则项参数,以稳定解减小k中噪声;当噪声水平低时,则需要减小正则项参数,加强保真项的逼近作用。

文献[14]中给出的λ取值为20,对不同的观测图像,这显然不是最优的参数。在式(1)中,由于λ作用在保真项上,因此,λ参数值的选择应与图像中的噪声水平成反比。

图像的局部结构信息可通过其梯度反映。对于图像中的点f( x,y),其梯度为g=∇f(x,y)。在f(x,y)的N×N邻域w,图像中点的局部梯度向量为:

那么点f(x,y)的局部梯度协方差矩阵可表示为:

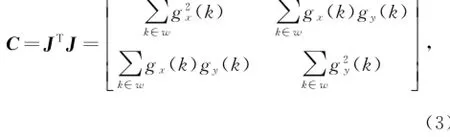
协方差矩阵SVD分解得到:

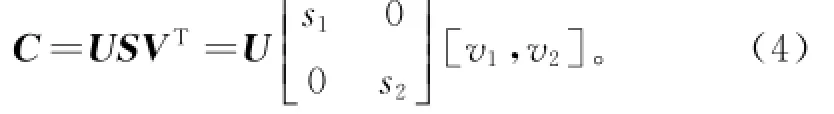
其中:U和V为正交矩阵;v1和v2分别为局部结构张量的主方向和次方向;特征值s1、s2分别为对应主方向和次方向上局部结构张量的能量大小,s1≥s2≥0。在图像平坦区域,s1≈s2≈0;在噪声污染区域, s1＞s2＞0。利用局部结构张量的特征值,局部结构的特征值指数度量[11]为:

图2为不同噪声方差下的度量c的值。从图2可看出,随着噪声水平的不断增加,c不断减小,因此,度量c能有效地表征图像的噪声水平。

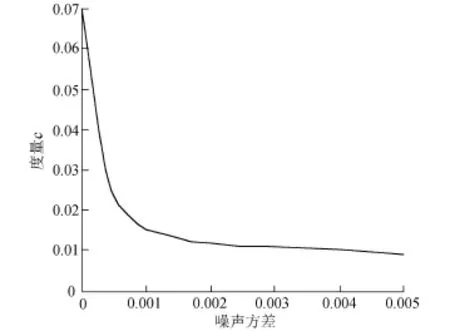
图2 度量c随噪声方差变化Fig.2 Trend of measure c with noise variance

综合上述分析和大量仿真验证,最终代价函数可表示为:

其中,λ取值为38+100c。当图像噪声水平低时,λ取较大值,侧重于逼近效果;当图像噪声水平高时,λ取较小值,侧重于解的稳定。

x更新的子问题可表示为:

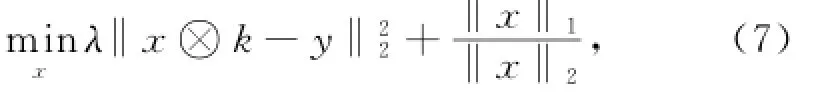
式(7)具有高度非凸性。解决方法是先给定x和k的初始值,然后交替更新x和k。

由于正则项‖x‖1/‖x‖2的存在,导致子问题的非凸性,若利用前一次迭代的‖x‖2的值,那么问题就变成了l1正则化的凸问题,可通过迭代阈值收缩算法快速解决[12]。

k更新的子问题可表示为:

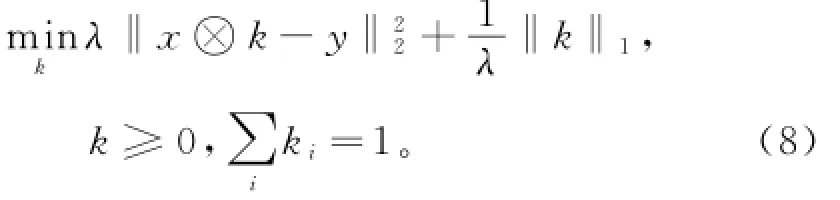
该问题可通过迭代加权最小二乘算法[13]解决,其中k到约束集的投影即设定非零元素为0,并重新归一化。

从实验结果可知,上述算法结构简单、效率高,且能精确地估计出PSF。而获得PSF的准确信息之后,利用经典的图像反卷积算法就可迅速地复原清晰图像,本研究采用Lucy-Richardson算法[14-15]。

3 实验结果及分析

本次实验中,采用模糊的星云和卫星观测图像进行测试,PSF均为13×13的高斯型,模糊后分别在图像中加入均值为0的高斯白噪声。为定量验证算法的复原效果,采用峰值信噪比(peak signal to noise ratio,简称PSNR)对复原结果进行评价,其定义为:

PSNR从统计意义上对图像进行衡量,忽视了图像本身像素之间的联系,评价结果与人的主观评价不完全吻合。结构相似法SSIM通过提取图像中的结构信息来衡量图像之间的相似程度,与PSNR相比,更接近人的主观评价。SSIM取值范围为0～1,越接近1说明与原始清晰图像越接近,即复原效果越好。

图3、4为2组图像经不同算法处理的结果对比,相应的复原指标见表1、2。

图3 卫星退化图像盲复原Fig.3 Blind restoration of degraded satellite image

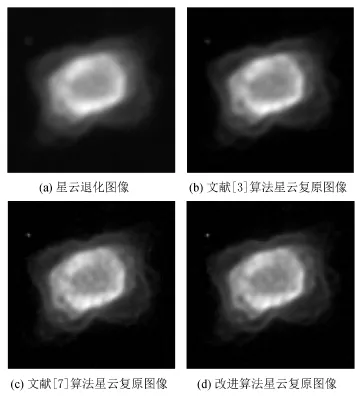
图4 星云退化图像盲复原Fig.4 Blind restoration of degraded nebula image

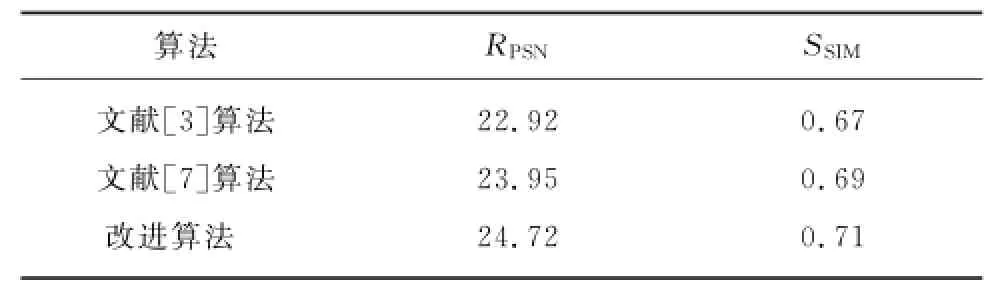
表1 卫星退化图像复原指标Tab.1 Restoration index of degraded satellite image

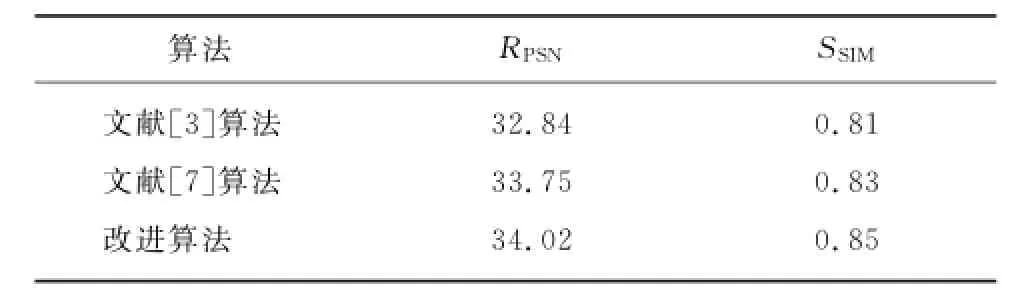
表2 星云退化图像复原指标Tab.2 Restoration index of degraded nebula image

从以上仿真结果和相应的复原指标可看出,与文献[3]算法相比,文献[7]基于稀疏测度的PSF估计算法能更为精确地估计出天文退化图像PSF,提高复原图像质量。而本算法通过自适应选择更加合理的参数,PSF估计精度进一步提高,恢复了更多的图像细节。

4 结束语

针对地基天文观测图像复原过程中,由于PSF准确信息的缺失引起的病态性和天文图像的特点,采用基于稀疏测度PSF估计算法,实现了天文图像PSF高精度估计。在此基础之上,结合反映图像噪声水平的指数度量,提出变正则化参数的改进PSF估计算法,并通过实验验证了改进的算法能更好地估计PSF的准确信息,恢复图像细节。

[1] Sheppard D G,Hunt B R,Marcellin M W.Iterative multiframe super-resolution algorithms for atmospheric turbulence-degraded imagery[J].Journal of the Optical Society of America,1998,5(4):978-992.

[2] Sun Libin,Cho S,Wang Jue,et al.Edge-based blur kernel estimation using patch priors[C]//IEEE International Conference on Computational Photography,2013: 1-8.

[3] Cho T S,Paris S,Horn B K P,et al.Blur kernel estimation using the radon transform[C]//IEEE Conference on Computer Vision and Pattern Recognition,2011:241-248.

[4] Joshi N,Szeliski R,Kriegman D.PSF estimation using sharp edge prediction[C]//IEEE Conference on Com-puter Vision and Pattern Recognition,2008:1-8.

[5] Levin A,Weiss Y,Durand F,et al.Efficient marginal likelihood optimization in blind deconvolution[C]// IEEE Conference on Computer Vision and Pattern Recognition,2011:2657-2664.

[6] Levin A,Weiss Y,Durand F,et al.Understanding and evaluating blind deconvolution algorithms[C]//IEEE Conference on Computer Vision and Pattern Recognition,2009:1964-1971.

[7] Krishnan D,Tay T,Fergus R.Blind deconvolution using a normalized sparsity measure[C]//IEEE Conference on Computer Vision and Pattern Recognition,2011:233-240.

[8] Shan Q,Jia J,Agarwala A.High-quality motion deblurring from a single image[J].ACM Transactions on Graphics,2008,27(3):73.

[9] Karayiannis N B,Venetsanopoulos A N.Regularization theory in image:the regularizing operator approach[J]. Optical Engineering,1989,28(7):761-780.

[10] Karayiannis N B.Regularization theory in image restoration-the stablizing functional approach[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1990,38(7):1155-1179.

[11] Coulon O,Alexander D C,Arridge S.Diffusion tensor magnetic resonance image regularization[J].Medical Image Analysis,2004,8(1):47-67.

[12] Beck A,Teboulle M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J].SIAM Journal on Imaging Sciences,2009,2(1):183-202.

[13] Levin A,Fergus R,Durand F,et al.Image and depth from a conventional camera with a coded aperture[J]. ACM Transactions on Graphics,2007,26(3):70-75.

[14] Lucy L B.An iterative techniquefor the rectification of observed distributions[J].The Astronomical Journal, 1974,79:745-750.

[15] Richardson W H.Bayesian-based iterative method of image restoration[J].Journal of the Optical Society of America,1972,62(1):55-59.

编辑:梁王欢

An improved astronomical image restoration algorithm based on sparsity measure PSF estimation

Shao Yunlong
(School of Information and Communication Engineering,Guilin University of Electronic Technology,Guilin 541004,China)

In order to overcome the blurring effect caused by atmosphere turbulence in ground-based astronomy,the PSF estimation algorithm based on sparsity measure is used to restore the accurate PSF information.An improved sparsity measure PSF estimation algorithm based on variational regularization parameters is proposed,which can adaptively correct the regularization parameter and improve the estimation precision of PSF.Experimental results show that the proposed algorithm can estimate PSF more accurately and the image restoration is improved.

ground-based astronomy;atmosphere turbulence;sparsity measure

TP391.41

:A

:1673-808X(2015)04-0310-05

2015-03-26

国家自然科学基金(61371107)

邵云龙(1988―),男,山东滨州人,硕士研究生,研究方向为天文图像复原。E-mail:shall_job@sina.com

邵云龙.基于稀疏测度PSF估计的天文图像复原改进算法[J].桂林电子科技大学学报,2015,35(4):310-314.