基于UPF的高动态北斗卫星信号的载波跟踪

王海辉,孙希延,纪元法

(桂林电子科技大学信息与通信学院,广西桂林 541004)

基于UPF的高动态北斗卫星信号的载波跟踪

王海辉,孙希延,纪元法

(桂林电子科技大学信息与通信学院,广西桂林 541004)

针对扩展卡尔曼滤波(EKF)和无迹卡尔曼滤波(UKF)等高动态信号载波跟踪算法存在跟踪精度不高的问题,采用无迹粒子滤波(UPF)算法对高动态北斗卫星信号载波进行跟踪。UPF算法结合粒子滤波(PF)和无迹卡尔曼滤波,采用PF对载波状态变量进行估计,同时使用UKF滤波器对粒子进行权值的重新分配,解决了粒子退化问题。通过Matlab仿真对比,基于EKF、UKF、UPF的跟踪算法的载波频率误差分别为―15～15、―10～10、―4～4 Hz,验证了UPF算法的优越性。

高动态;多普勒频率;无迹卡尔曼滤波;粒子退化;粒子滤波

高动态卫星信号的载波跟踪由于涉及国防军事安全,各国都将其作为军事机密进行严格监管。传统的高动态卫星信号载波跟踪算法主要有扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)等[1-3]。EKF载波跟踪算法利用泰勒级数对非线性函数进行一阶线性展开,泰勒展开过程忽略了高阶项,因此载波跟踪精度不高且需要计算雅可比矩阵,然而高动态卫星信号状态的测量方程雅可比矩阵不易计算甚至不存在。针对EKF载波跟踪存在的问题,研究人员提出了基于无迹变换(UT)的UKF高动态信号载波跟踪算法。UKF滤波算法直接对高动态信号的多普勒频移及其变化率等状态变量的概率密度函数进行估计,在信号的跟踪过程中无需对非线性的测量函数作泰勒级数展开及计算雅可比行列式。信号跟踪精度直接影响导航接收机的位同步、帧同步和导航电文的解调,然而基于EKF、UKF高动态北斗卫星信号的载波跟踪算法的精度有限。

鉴于此,结合粒子滤波(PF)[2]和UKF,采用粒子滤波对载波跟踪过程的状态变量进行估计,每一个跟踪历元以UKF算法对粒子滤波中的粒子进行权重的重新分配,防止粒子的退化。

1 高动态北斗卫星信号

在相对卫星高速运动的北斗卫星信号接收载体中,位移、速度、加速度、加加速度分别为[4]:

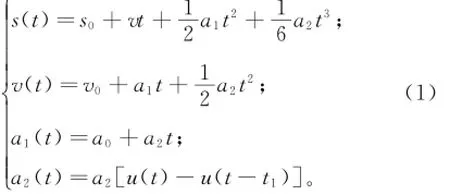
在卫星信号接收载体的运动过程中,载体运动变量与多普勒角频移变量的关系为:

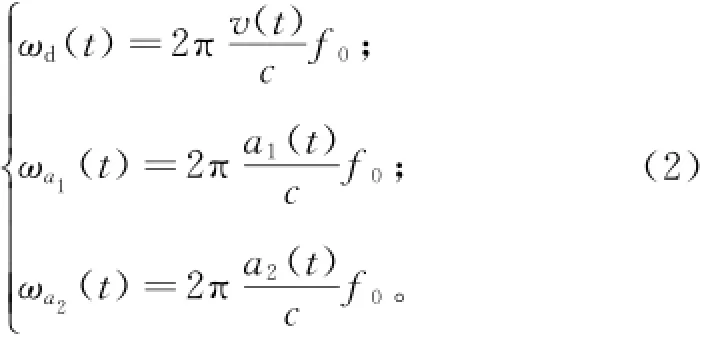
由式(1)、(2)可知,载波多普勒频移为:

式(1)、(2)、(3)中,位移s(t)、速度v(t)、加速度a1(t)、加加速度a2(t)分别对应高动态北斗信号中的多普勒相位θ、多普勒角频率ωd、多普勒角频率变化率ωa1、多普勒角频率二阶变化率ωa2。在实际高动态导航接收载体中,经过下变频以及AD转换后,高动态北斗卫星B1频点中频信号为[5]:

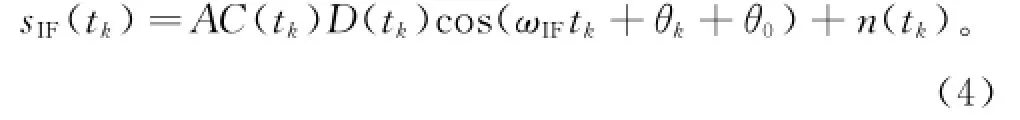
其中:θk为多普勒相移;θ0为初始相位;n(tk)为噪声;ωIF为中频信号角频率;A为信号幅度;C(tk)为伪随机码;D(tk)为导航电文。

2 载波跟踪环路的设计

2.1 载波跟踪框图

基于UPF的高动态北斗卫星信号的载波跟踪环路如图1所示[1-4]。

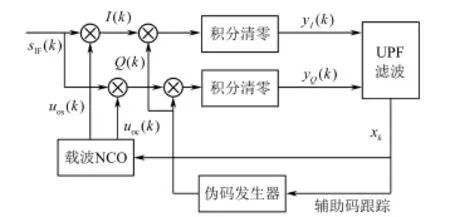
图1 基于UPF的载波跟踪环Fig.1 The carrier tracking loop based on UPF

基于UPF的载波跟踪环路通过压控振荡器(NCO)产生本地正弦余弦信号与接收机下变频后的卫星数字中频信号混频得到2路数字采样信号I(k)、Q(k)。I、Q分量与北斗接收机的伪码发生器产生的即时码做相关运算对伪码进行剥离,剥离伪码的北斗卫星信号经积分清零低通滤波器后输出相干积分值yI(k)、yQ(k)。UPF跟踪算法将yI(k)、yQ(k)作为UPF滤波器的观测值对卫星信号的载波相位差、多普勒频移、多普勒频率变化率及二阶变化率进行估计。UPF滤波器估计值控制载波NCO复现信号与接收的北斗卫星信号混频后对载波进行剥离。

2.2 状态方程和测量方程

图1中载波NCO控制产生的本地信号为:其中:ω0为载波NCO复现的角频率;θ1为复现初始相位。

载波NCO产生的信号式(5)和本地信号式(4)混频后累加作为主UPF滤波器的测量值:其中:ωek、θek分别为中频信号混频后第k积分时刻的多普勒角频差nI(k)和多普勒相位差nQ(k)累加后的噪声;T为积分时间间隔;R(Δτk)为伪随机码自相关函数。

设k时刻高动态信号载波多普勒相位为θk、多普勒角频率为、多普勒角频率变化率为、多普勒角频率二阶变化率为,由式(3)可知,k+1时刻载波的多普勒变量为:

基于UPF的载波跟踪算法建立的非线性模型为:

式(8)、(9)分别为状态方程和测量方程。其中:Xk、Yk分别为k时刻系统的状态变量和观测变量;h(·)为高动态信号中状态变量与测量值的映射关系;φ为状态转移矩阵;Qk为过程噪声协方差矩阵;Rk为观测噪声方差矩阵。

由式(7)可知,UPF滤波器的状态向量Xk= [θkωk

dωka1ωka2]T,状态转移方阵

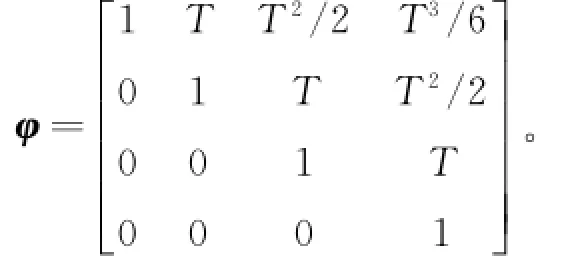
其中噪声qk=[qk1qk2qk3qk4]T[5]:

噪声qk的协方差矩阵

其中,Ny为过程噪声单边功率谱密度。

由式(6)可知,在高动态北斗卫星信号跟踪中, UPF滤波器的测量值为:

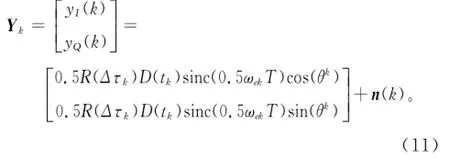
载波跟踪过程中,假设信号的伪码完全同步,则 R(Δτk)=1,由于ωekT远远小于π/2,则sinc(1/2ωekT)=1。简化后UPF滤波器的测量值为:

其中,测量噪声n(k)=[nI(k)nQ(k)]T为零均值,方差为σ2的高斯白噪声。其协方差矩阵为:

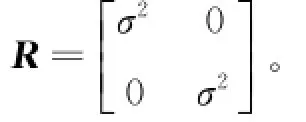
设L=[1 0 0 0]T,则θk=LXk,高动态北斗卫星信号的载波跟踪过程的测量方程与状态变量关系为:

3 UPF滤波算法

采用UPF[6-8]滤波器估计高动态北斗卫星信号的状态变量。

初始化粒子:

采用UKF更新粒子[9-10]:

Sigma点的选取和时间更新:

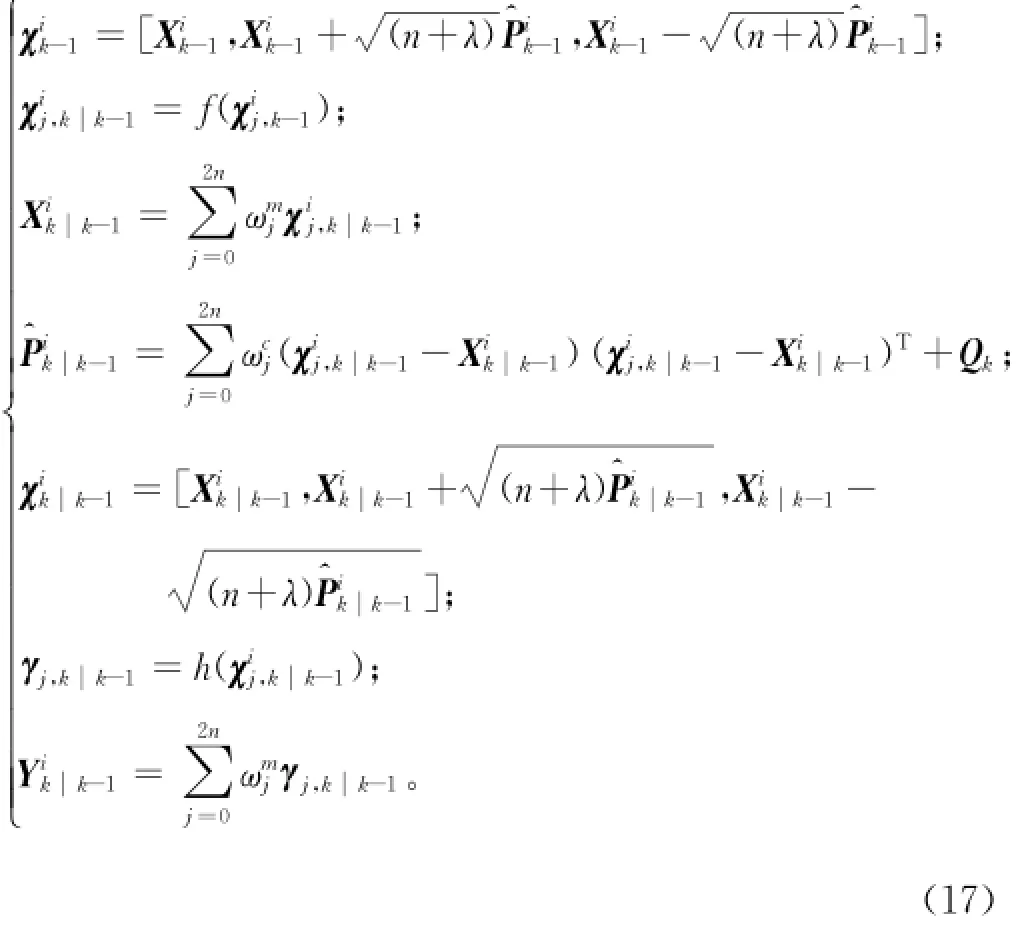
其中:

测量更新:

计算粒子权值:

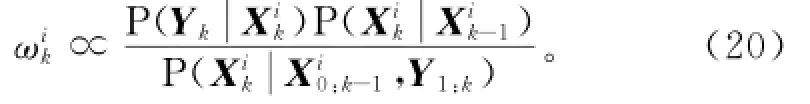
归一化粒子权值为:

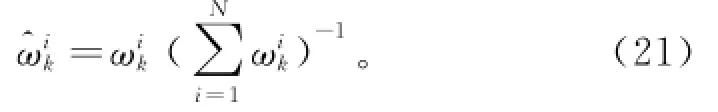
输出状态变量:

i=1

输出状态协方差矩阵:

进行粒子重采样:

其中:X0为初始化状态变量;^P0为初始状态协方差矩阵;n为状态变量的维数;λ=ξ2(n+κ)―n为比例因子,κ为辅助尺度因子;ξ为散布程度因子;β为验前分布因子;ωjm为均值的加权系数;ωcj为方差的加权系数;j=1,2,…,2n。重复计算式(16)～(24),递归完成UPF过程。

4 仿真分析

仿真采用美国喷气推进实验室(JPL)提出的高动态模型[10]。

4.1 Matlab仿真参数设置

UPF中仿真参数设置为:

1)北斗卫星导航电文D(t)为随机产生的二进制码;

2)北斗卫星为2号卫星;

3)中频频点为1.42 MHz;

4)采样频率为10 MHz;

5)相干积分时间T=1 ms;

6)粒子滤波粒子点数为100;

7)状态变量初始值X0=[0―2000―5000]T;

8)初始状态协方差和测量噪声协方差:

9)无迹变换中ξ=1.027,β=2,κ=0。

4.2 仿真对比

利用EKF、UKF、UPF算法对JPL高动态运动模型的北斗卫星信号进行载波跟踪和算法性能对比。基于UPF的跟踪环路对高动态北斗卫星信号的多普勒频移跟踪误差如图2所示。从图2可看出,UPF滤波器的跟踪环路起始时刻经过60 ms的抖动后跟踪误差趋于稳定。在3000、5500 ms时刻由于受JPL加加速度突变,环路多普勒频移跟踪误差瞬间增大, UPF滤波器跟踪环路经过约50 ms环路输出的多普勒频移误差稳定在―4～4 Hz。

图2 UPF多普勒频移跟踪误差Fig.2 Doppler shift tracking error of UPF algorithm

EKF、UKF、UPF滤波算法的多普勒频移误差对比如图3所示。从图3可看出,EKF、UKF、UPF滤波算法对JPL高动态信号模型跟踪的误差范围为―15～15、―10～10、―4～4 Hz,UPF的滤波精度高于EKF、UKF高动态跟踪算法。

图4为跟踪环路中作为UPF滤波器测量值的同相、正交2路积分清除值。从图4可看出,起始时刻60 ms左右,由于跟踪环路并未准确地跟踪多普勒频移,同相、正交2路积分清除值出现错误。在3000、5500 ms时刻受加加速度突变的影响,跟踪环路中同相、正交2路积分清除值有约30 ms突变,但对跟踪环路后期信号解调不会产生影响。

图3 多普勒频移误差对比Fig.3 The comparison of Doppler shift error

图4 同相和正交2路积分清除值Fig.4 Integrate-clear value in in-phase and quadrature channel

5 结束语

以高动态北斗卫星信号的载波多普勒频移精确跟踪为研究背景,在PF滤波和UKF滤波的基础上,采用无迹粒子滤波(UPF)算法,实现了对高动态北斗卫星信号的精确跟踪。Matlab仿真分析表明,相比EKF、UKF跟踪算法,UPF跟踪算法对高动态的北斗卫星信号的载波跟踪精度有明显提高,对于我国高动态北斗卫星信号的跟踪有一定的应用价值。

[1] Li Weibin,Liu Shanjian,Zhou Chunhui,et al.High dynamic carrier tracking using Kalman filter aided phaselock loop[C]//Proceedings of 2007 International Conference on Wireless Communications,Networking and Mobile Computing,2007:60-68.

[2] 焦尚彬,周秀萍,黄伟超,等.高动态GPS载波跟踪算法研究[J].系统仿真学报,2012,24(6):1270-1276.

[3] Zhu Yunlong,Liu Zhongkan,Zhang Qishan,et al.Frequency estimation algorithm for high dynamic GPS receivers based on UKF[C]//Proceedings of the 2nd International Conference on Space Information Technology,2007:65-70.

[4] 谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009:295-320.

[5] 中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件公开服务信号B1I(1.0版)[EB/OL]. [2015-03-16].http://www.beidou.gov.cn/attach/2012/ 12/27/2012122755318f7eabbe451aa6d052f829f92e50.pdf.

[6] 朱志宇.粒子滤波算法及其应用[M].北京:科学出版社,2010:37-42.

[7] Julier S J,Uhlmann J K.Unscented filtering and nonlinear estimationg[J].IEEE Transactions on Signal Processing,2004,92(3):401-422.

[8] 张苗辉,刘先省.基于无味粒子滤波的动态场景下高机动目标跟踪[J].光电子,2010,21(6):924-927.

[9] 冯琼华,吴铁军,马龙华.高动态下基于AUKF的载波跟踪算法[J].计算机工程,2012,8(16):238-244.

[10] Vilnrotter V A,Hinedi S,Kumar R.Frequency estimation techniques for high dynamic trajectories[J].IEEE Transactions on AES,1989,25(4):559-577.

编辑:曹寿平

Carrier tracking of high dynamic BD satellite signal based on UPF

Wang Haihui,Sun Xiyan,Ji Yuanfa
(School of Information and Communication Engineering,Guilin University of Electronic Technology,Guilin 541004,China)

In order to improve the tracking accuracy of extended Kalman filter and unscented Kalman filter and other high dynamic signal carrier tracking algorithms,the unscented particle filter is used for tracking the high dynamic Beidou satellite signal carrier.The UPF algorithm combines particle filter with unscented Kalman filter,the carrier state variables are estimated by particle filter,and to solve the problem of particle degradation,the UKF filter is used to redistribute the weight of particles.Matlab simulation results show that the carrier frequency offsets of EKF,UKF and UPF tracking algorithms are respectively―15-15,―10-10,―4-4 Hz,the superiority of UPF algorithm is proved.

high dynamic;Doppler frequency;unscented Kalman filter;particle degeneration;particle filter

TN967.1

:A

:1673-808X(2015)04-0259-05

2015-03-16

国家自然科学基金(61162007,61362005);广西无线宽带通信与信号处理重点实验室主任基金(GXKL0614102);桂林电子科技大学研究生教育创新计划(2013010007)

孙希延(1974―),女,山东安丘人,研究员,博士,研究方向为信号处理、卫星导航。E-mail:sunxiyan1@163.com

王海辉,孙希延,纪元法.基于UPF的高动态北斗卫星信号的载波跟踪[J].桂林电子科技大学学报,2015,35(4):259-263.