狭义相对论与钟慢效应关系再认识——纪念狭义相对论创立110周年<br/>

狭义相对论与钟慢效应关系再认识——纪念狭义相对论创立110周年

2015-01-04文兴吾

成都工业学院学报 2015年3期

文兴吾*

(四川省社会科学院哲学与文化研究所，成都 610071)

狭义相对论与钟慢效应的关系问题，学术界一直存在不同的观点。《大学物理》1997年第4期发表《狭义相对论解决双生子佯谬之不可能》［1］后，相继在1999年第6期发表了《孪生子效应析疑》［2］，2001年第4期发表了《哪一个钟慢了?——关于相对论中钟慢效应的进一步讨论》［3］，2009年第10期发表了《基于同时的相对性对钟慢尺缩效应的再认识》［4］。这些文章反映了人们对明晰认识狭义相对论与钟慢效应之间关系的努力。

2005年是爱因斯坦(Albert Einstein)建立狭义相对论100周年和逝世50周年的纪念年，笔者在《世界科技研究与发展》上发表了《狭义相对论与丁格尔时钟悖论——对一场著名争论的回顾与再认识》［5］，对20世纪60年代英国《自然》杂志上，由英国著名光谱学家、天体物理学家、科学哲学家，曾任皇家天文学会会长的H.丁格尔(Herbert Dingle)引起的那场争论，进行重新认识，对丁格尔时钟悖论的性质进行了重新分析。丁格尔分别于1962年、1963年、1967年在《自然》杂志上发表论文争辩:狭义相对论存在“时钟悖论”，因此是有问题的。诺贝尔物理学奖获得者、《爱因斯坦的相对论》(1920年德文版、1924年英文版)一书的作者M.玻恩(Max Born)曾参与争论，《自然》杂志编辑部1967年发表了评论文章。这是笔者继20世纪90年代在《中国社会科学》和《大自然探索》杂志提出“相对论时空理论再认识”［6］和“爱因斯坦‘尺缩’‘钟慢’效应再认识”［7］的15年后，再一次在学术界辨析爱因斯坦“钟慢”效应与狭义相对论的关系。中国人民大学书报资料中心复印报刊资料《科学技术哲学》2005年第6期全文转载了笔者这篇纪念文章。

本文从一个不为人们重视的关键问题入手，即从爱因斯坦建立狭义相对论的科学方法与狭义相对论理论的逻辑构成入手，综合运用A·P·弗伦奇(A.P.French)在国际著名的改革教材“美国麻州理工学院物理学导论丛书”第二卷《狭义相对论》中的一些研究观点和闵可夫斯基理论，阐明狭义相对论与钟慢效应之间的正确关系。以此纪念爱因斯坦建立广义相对论100周年和建立狭义相对论110周年。

一、从建立狭义相对论的科学方法谈起

狭义相对论是爱因斯坦运用“假说—演绎”法建立的。

演绎法由亚里士多德首先作出有系统的研究，他建立了以三段论法为中心的形式逻辑，并把他的发现运用到理论研究。2 300多年前完成的欧几里德《几何原本》，是运用演绎法进行科学研究的典范，它从“等量加等量还是等量”等5条公理和“任意2点间可以作一条直线”等5条公设出发，推演出467个几何命题，使几何学成为历史上第一个严密的科学体系。近代科学早期，弗兰西斯·培根(Francis Bacon)重视实验归纳法而轻视演绎法，认为演绎法的结论包含在前提之中，并不产生新知识。在同时期的笛卡儿(Rene Descartes)看来，培根强调知识来自经验是正确的，但培根本末倒置了:经验诚然重要，但往往并不可靠，以它为基础进行推理很容易发生错误。笛卡尔开始考虑创立一种包含几何学和形式逻辑这两种科学的优点的新方法，这种方法既能推理严密，又能获得新知识。笛卡儿的探索在爱因斯坦那里结出了硕果。爱因斯坦在建立狭义相对论一开始，就运用了“假说演绎法”。爱因斯坦把有一定经验事实支持的两个猜想(假说)提升为公设，其一是把在力学领域已成为真理的伽利略相对性原理推广到电磁学领域，其二是认为真空中光速不变，与发射体是静止还是作匀速运动无关。前者，后来称为“狭义相对性原理”;后者，则称为“光速不变原理”。从这两条公设出发，爱因斯坦通过(数学)逻辑推导，建立起了狭义相对论

对于运用演绎法进行科学探索，爱因斯坦设计了一个模式，如图1所示［8］541，其中Σ是直接经验，A是公理或一般性的假设，由它们推出一定的结论来。这样，演绎推导使我们由A通过逻辑道路得出各个个别结论S。然后S可以同Σ相联，这也就是所谓的用实验来验证。

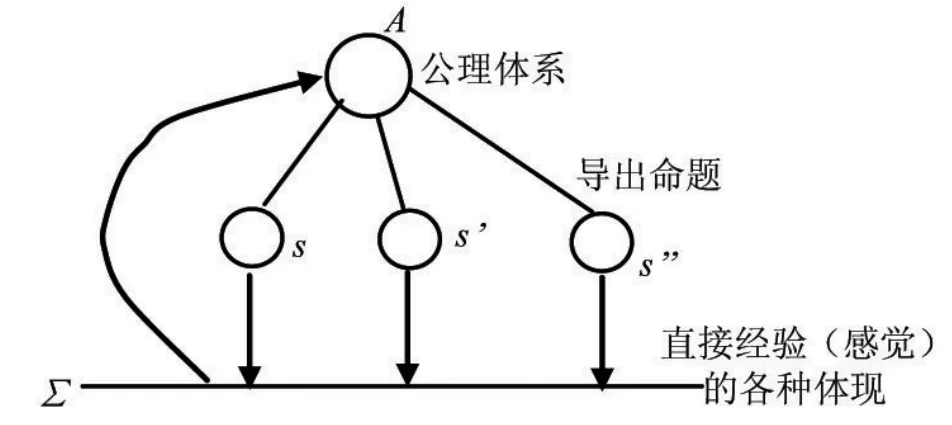
图1 爱因斯坦对运用演绎法建构理论的诠释

在明确了爱因斯坦建立狭义相对论所运用的“假说—演绎”法的基本特征后，笔者指出:对于狭义相对论与钟慢效应之间关系认识，过去人们注重的只是图1中的“第二步”，即“导出命题”与“直接经验”(实验)的关系;而没有重视“第一步”，即“公理体系”与“导出命题”的关系。这显然是有重大缺陷的。试想，如果从狭义相对论的理论前提不能导出“钟慢效应”，那么，讨论“第二步”还有什么意义呢?

二、爱因斯坦从狭义相对论导出钟慢效应的合理性辨析

爱因斯坦1905年创立狭义相对论的论文，在引言中提出2个公设后，随即在“运动学部分”首先讨论了“时间”及“同时性的定义”。他“借助于某些(假想的)物理经验，对于静止在不同地方的各只钟，规定了什么叫做它们是同步的，从而也就获得了‘同时’和‘时间’的定义”［9］86。在此基础上，爱因斯坦运用“光速不变原理”和“相对性原理”，推导出了“从静系到另一个相对于它做匀速移动的坐标系的坐标和时间的变换理论”，即“洛仑兹变换方程”。

在得到洛仑兹变换方程后，爱因斯坦进而讨论了“关于运动刚体和运动时钟所得方程的物理意义”。其中，他写道:“进一步，我们设想有若干只钟，当它们同静系相对静止时，它们能够指示时间t;而当它们同动系相对静止时，就能够指示时间τ，现在我们把其中一只钟放到k的坐标原点上，并且校准它，使它指示时间τ。从静系看来，这只钟走得快慢怎样呢?

在同这只钟的位置有关的量x，t和τ之间，显然下列方程成立:

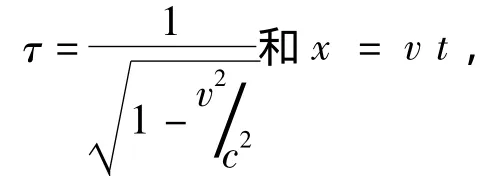
爱因斯坦的上述讨论是把洛仑兹变换与图2所示的过程相联系，从而得出“运动的钟变慢”的结论。

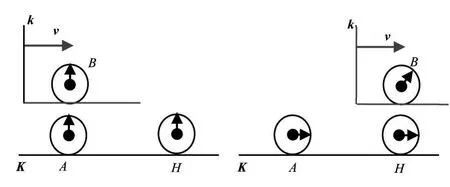
图2 爱因斯坦得出钟慢效应时所对应的物理过程

20世纪60年代，A·P·弗伦奇事实上已经指出了爱因斯坦从上述推导得出“运动的钟走慢了”的结论是错误的。他写道:爱因斯坦推导出的结果△t=△τ/(1-v2/c2)1/2只是表明“在单一时钟上所记录到的时间流逝与相对于该时钟为运动的参照系中的测量结果进行比较……单一时钟上测得的时间间隔(本征时)小于在另一参照系中的描述这一间隔起止时刻的两时钟读数(坐标时)之差。单一时钟所测得时间的标度在表面上被拉长了，因此有时间膨胀这种措辞用以描述它。”［10］105。他还写道，“把时间膨胀简单地说成‘运动的钟走慢了’……可能引起误解。第一，这一陈述似乎暗示，同相对论的观念相反，这里存在某种绝对依赖于运动的东西。第二，同样令人遗憾的是，它暗示时钟本身的运转发生了某种本质的改变，亦即暗示时钟运转的物理基础发生了某种改变。然而，狭义相对论的中心特征却是相反的情况真实，即如时钟自身所在的参照系中所描述的，时钟的运转完全不受影响。”［10］110

对于导致“时间膨胀”的原因，弗伦奇指出:依据洛仑兹变换所得到的结果△t=△τ/(1- v2/c2)1/2，“实质上不仅包含单一时钟的时率，而且也包含为不同时钟整步的程序。……在运用洛仑兹变换时，我们假定这种整步的程序已经完成，而作为观测现象的时间膨胀则是其必然的结果。”［10］106

把“时间膨胀”公式△t=△τ/(1-v2/c2)1/2与弗伦奇给出的“用于讲演时间膨胀的光-脉冲钟”(如图3 所示)［10］112相结合，能够对“‘时间膨胀’本质上是由爱因斯坦的‘对钟’程序所决定”作出很明晰的说明。弗伦奇并没有完成这项工作，笔者在文献［5］中完成了。

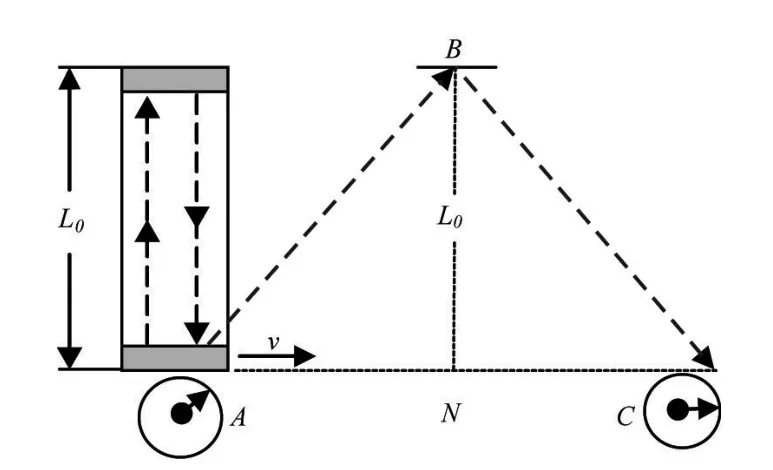
图3 用于讲演时间膨胀的光-脉冲钟

当前，要纠正爱因斯坦的错误已经更加复杂了。在狭义相对论的发展史上，1911年爱因斯坦为反驳V·瓦里恰克(V.Varicak)的说法——按照洛仑兹的观点，一个运动物体在运动方向上的收缩是一种客观地发生着的变化;而按照爱因斯坦的观点，收缩不是一个物理事实而是由我们调整时钟和测量长度的方式所引起的一种主观现象——作出了“关于洛仑兹收缩是否事实上存在的问题，是引人误解的。它‘事实上’并不存在，因为它对于一个运动观察者是不存在的;但是它‘事实上’却又确实存在，也就是说它是如此地存在，即从一个并非相随运动的观察者看，它在原理上是可以利用物理手段来探测的”［11］论断。其后，M·玻恩写道:“上面的论述同样适用于时间的相对性。理想钟在它静止的那个参考系里总是用相同的速率走动，它指出的乃是该参考系的‘原时’。但从另一个参考系来看时，它走得慢了;在这个参考系里，一个确定的原时间隔似乎变得比较长了。在这里如果问事件的‘真实的’时间长短是什么，同样也是没有意义的。”［12］在这些论述的引导下，人们已经有了这样的思维:对于时钟静止的那个参考系而言，时钟的走时率并没有改变;但是对于时钟相对运动的参考系而言，就其原理上是可以利用物理手段来探测的，时钟的走时率确实改变了。对于两个相对运动的参考系，你看我的钟变慢、我看你的钟变慢，这也是对称的，是与否定绝对优越惯性系的相对论精神一致的。文献［3］和［4］就是坚持着这样的观点。例如文献［3］写道:“两个作相对运动的观察者互相认为对方的钟走时率慢了，问题出在对钟上。按相对论理论，两参考系各处的钟不能同时对准。一参考系内各处相互对准了的钟，在另一参考系看来是没有对准的。对钟问题对理解相对论的原理是至关重要的。”

应该明确，文献［3］和［4］都阐明了钟的快慢有2个含义:其一是钟表指针的运动速度，即走时率的大小;其二是钟表指针的超前和滞后(走时率可以相同)，与钟表的零点校正有关。那么，就不应该在讨论中又把两者给混淆起来:从“对钟”引起的“时间膨胀”，得出“运动的钟变慢”的结论。尤其是文献［4］还引用了弗伦奇的观点。依据狭义相对论的内在逻辑，对钟程序是没有任何神秘可言的，绝不可能从“钟表的零点校正”而引出“钟表指针的运动速度，即走时率快慢”发生变化;20世纪90年代，笔者在文献［6］和文献［7］中就已经作出过较透彻的解析与阐述。

把对钟引起的“时间膨胀”说成“运动的钟变慢”，其悖理问题是容易显现出来的。例如，我们在图2中再设置一个惯性系K＇，k相对于K＇以速度u运动。对于时钟B相对于K系和K＇系运动，由洛仑兹变换式，K系和K＇系测得的时间间隔分别为:

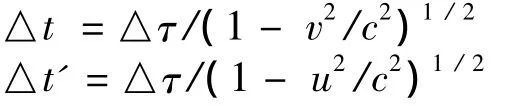
由于 v≠u，故△t≠△t＇。对此，按照对钟引起的“时间膨胀”的认识，是不存在任何问题的。但是，按照“运动的钟变慢”的认识，只能承认两者的差异是由相对运动速度v≠u导致，于是，“同相对论的观念相反，这里存在某种绝对依赖于运动的东西”。按照伽利略—爱因斯坦相对论原理，一个物质系统无论是静止还是作匀速直线运动，其内部的运动和变化的每一个物理过程都不会有所改变——在这里，回顾一下伽利略相对性原理是有教益的。伽利略(Galileo Galilei)仔细观察与研究了在平稳前进的船舱内的力学现象，他注意到，把人关在大船的船舱里，观察桌上摆着的小球，水碗里的鱼，飞行着的苍蝇，或者自己在船舱里跳跃或扔东西，不管船以何种速度前进，只要船的运动是匀速的，而不是忽快忽慢、忽左忽右摆动的，你将无法从其中任何一个现象来确定:船是运动的还是停着不动的。对此进行理论概括，既可以说:在不同惯性系内，力学现象的规律是一样的，所以不可能通过力学实验来判断所在的惯性系是处于静止还是在作匀速直线运动;也可以说:物质系统内在运动变化所遵从的规律不因该系统是静止还是在作匀速直线运动而有所改变;还可以说:物质系统的匀速直线运动对物质系统的内在运动变化过程并无影响——由此可得:在狭义相对论中，时钟的走时率是一个不变量，不因时钟与惯性系的相对运动速度不同而有所改变。

三、“四维时空”理论给出了狭义相对论关于时钟问题的“内在完备性描述”

众所周知，闵可夫斯基(H.Minkowski)在1908年用“四维时空”理论重新诠释了狭义相对论，爱因斯坦在1916年就把“四维时空”理论看作是狭义相对论时空理论的完善形式。按照“四维时空”理论，对于图2中钟B由xA到达xH的这一过程，k系和K系的时间、空间以及时—空测量值分别为:

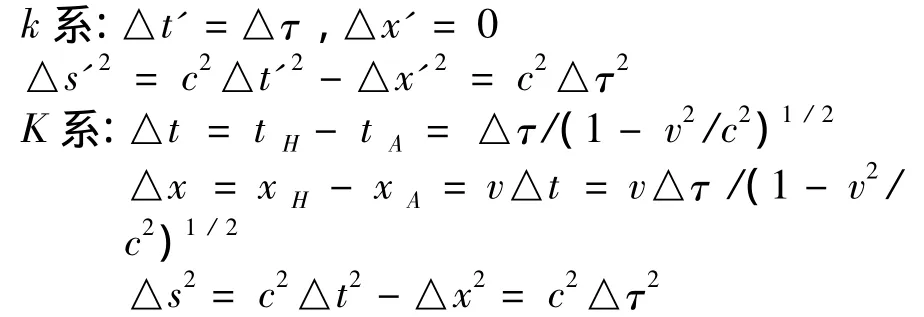
可见，k系和K系对上述物理过程进行的时空描述，尽管时间、空间测量值各不相同，但“四维间隔”却相同，都是c2△τ2。这说明:狭义相对论的“时间膨胀”—— “坐标时”大于“本征时”——并不意味运动的钟比静止时走慢了。

对于“四维间隔不变量”的物理意义，一些著名的相对论教科书有很清晰的阐述。爱因斯坦作序，认为“具有系统性及逻辑上的完整性”的P·G·柏格曼(P.G.Bergmann)的《相对论引论》一书作出了如下表达:

“考虑空间与时间坐标分别为(x1，y1，z1，t1)与(x2，y2，z2，t2)的两个事件。时间间隔的平方与距离的平方除以c2之差称它为，或

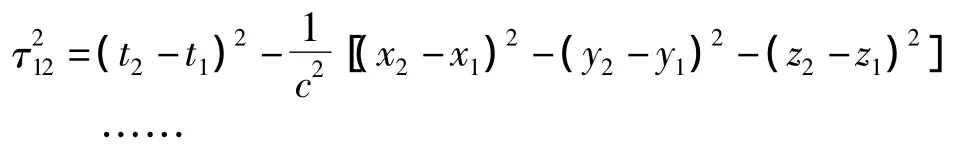
至此，我们看到:按照“四维时空”理论所规定的程序进行操作所获得的“四维间隔不变量”△τ，也就是作为狭义相对论理论前提的狭义相对性原理所断言的“一个钟无论是静止还是作非变速运动，它的走时率都不改变”的理论对应。狭义相对论在时钟问题上，严格满足着爱因斯坦等在1935年提出的一个物理理论应该遵从的完备性条件:“物理实在的每一元素都必须在这物理理论中有它的对应”［8］329。

四、光钟实验与狭义相对论

2010年9月24日美国《科学》杂志发表了美国国家标准技术研究院(NIST)C.W.Chou等的论文《光钟与相对论》，阐述了他们利用当时世界上最精确的一对铝原子钟所做的验证爱因斯坦关于狭义相对论的“钟慢效应”和广义相对论的“钟慢效应”观点的两个实验。［14］

C.W.Chou等研制出的铝原子钟，精准度为运行37亿年后误差不超过±1 s。利用2个完全相同的铝原子钟，他们进行了如图4所示的2组“对比实验”:左图为实验1，右图为实验2。

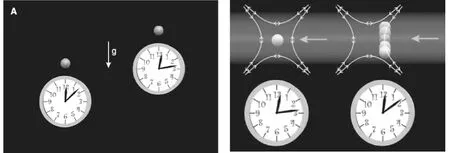
图4 以铝原子钟验证相对论“钟慢效应”示意图［14］

在实验1中，C.W.Chou等将放置原子钟的2个桌子中的一个桌面升高了33 cm，发现位置低的原子钟比位置高的原子钟运行得慢。两者差异为:高处的钟比低处的钟每年快11.4×10-8s。这一结果证实了爱因斯坦广义相对论关于引力场越强的位置、时钟运转越慢的理论。

在实验2中，C.W.Chou等改变其中一个原子钟的电场，使铝离子以约10 m/s的速度进行震荡，然后观察运动中的铝原子钟与静止的铝原子钟的时间差异。他们发现这个在运动的铝原子钟的时间，大概比静止的铝原子钟慢了10-16s。接着，他们改变电场来控制铝离子震荡的速度，发现结果与爱因斯坦给出的狭义相对论“时间膨胀”公式△t=△τ/(1-v2/c2)1/2相一致。

然而，在我们再一次阐明狭义相对论关于时钟问题的“内在的完备性观点”后，不难看到:周勤文等声称证明了爱因斯坦关于狭义相对论的“钟慢效应”观点的那个实验——在一个铝原子钟内，对作为光钟“内核及载体”的铝离子施加不断变化的电磁场，使其进行往复运动，相当于每秒运动约10 m;与“未施加作用”而被视为“静止”的另一个铝原子钟的走时情况相比较，被“施加作用”而“运动的钟”每秒慢了10-16s——是与狭义相对论关于运动的时钟节率的判断不相关联的。狭义相对论设定运动的钟作“匀速直线运动”，而这里却是来回往复的“变速运动”。因此，这个实验的意义，同样是对爱因斯坦关于广义相对论的“钟慢效应”观点的证明，并且是对等效原理的新证明。

五、结语

1905年，爱因斯坦在创立狭义相对论的论文中得出“钟慢效应”的结论是不合理的;事实上，从狭义相对论中是得不出“运动的钟比静止时走得慢”这种结论的。既然从狭义相对论根本得不出“运动的钟比静止时走得慢”这种结论，那么也就不能把“钟慢效应”实验证据与△t=△τ/(1-v2/c2)1/2在数值上的符合，看作是对狭义相对论的证明。狭义相对论断言的是相反的情况真实:匀速运动的时钟与静止的时钟，“内在的”时间变化是相同的。

［1］孟广达，王润华，霍瑞云，等.狭义相对论解决双生子佯谬之不可能［J］.大学物理，1997(4):22-26.

［2］罗蔚茵，郑庆璋.孪生子效应析疑［J］.大学物理，1996(6):1-5.

［3］罗蔚茵，赵凯华.哪一个钟慢了?:关于相对论中钟慢效应的进一步讨论［J］.大学物理，2001(4):15-16.

［4］王景雪，汤正新，陈庆东，等.基于同时的相对性对钟慢尺缩效应的再认识［J［.大学物理，2009(10):24-27.

［5］文兴吾.狭义相对论与丁格尔时钟悖论:对一场著名争论的回顾与再认识［J］.世界科技研究与发展，2005(2):72-77.

［6］文兴吾.相对论时空理论再认识［J］.中国社会科学，1990(5):29-42.

［7］文兴吾.对爱因斯坦“尺缩”，“钟慢”效应的再认识［J］.大自然探索，1991(2):109-117.

［8］爱因斯坦.爱因斯坦文集:第一卷［M］.许良英，李宝恒，赵中立，译.北京:商务印书馆，1976:541，329.

［9］爱因斯坦.爱因斯坦文集:第二卷［M］.范岱年，赵中立，许良英，译.北京:商务印书馆，1977:86，96，85，85-86.

［10］弗伦奇.狭义相对论［M］.张大卫，译.北京:人民教育出版社，1979:105，110，106，112.

［11］爱因斯坦.爱因斯坦全集:第三卷［M］.戈革，译.长沙:湖南科学技术出版社，2002:381-382.

［12］玻恩.爱因斯坦的相对论［M］.彭石安，译.石家庄:河北人民出版社，1981:283.