基于主成分分析法土地储备风险的定量评估
2015-01-03朱家明程倩倩朱海龙
朱家明,程倩倩,朱海龙
(安徽财经大学 a.统计与应用数学学院;b.管理科学与工程学院,安徽 蚌埠 233030)
基于主成分分析法土地储备风险的定量评估
朱家明a*,程倩倩b,朱海龙a
(安徽财经大学 a.统计与应用数学学院;b.管理科学与工程学院,安徽 蚌埠 233030)
针对土地储备方案的风险评估,使用Excel对所给土地储备方案的相关数据筛选和处理,其次采取主成分分析、模糊C均值聚类分析和正态性检验等方法,建立了土地储备方案风险等相关的评价模型。运用Matlab编程,得到了主要通过建立风险评价指标来衡量土地储备方案的总风险,并确立相应的风险评价标准,得到了对土地储备风险进行有效评估的方法。
土地储备;风险评价指标;聚类分析;正态性检验;Matlab
土地收储能够在增加地方的财政收入、加快经济建设、提高生活水平以及改善城市的基础设施建造等方面发挥积极作用,但同时也带来相应的风险。在土地收储过程中,需要动用大量资金,而这仅仅依靠政府的财政收入是不现实的。于是在土地收储过程中往往伴随着大量的银行信贷、抵押贷款等。在土地市场环境较好的情况下,其风险是不易显见的,而当土地市场出现疲软时,往往会导致因土地无法变现而导致金融风险的集中爆发。因此,衡量土地储备过程中的风险具有十分重要的意义。
一、数据的获取及假设
数据来源于2014第七届“认证杯”数学建模网络挑战赛C[1]。为便于分析,提出以下假设:1)在内部风险中,只考虑从财务风险来选取风险评价指标,其他风险如经营风险不作考虑;2)在外部风险中,只考虑从社会风险和稳定性风险角度选取评价指标,其他风险如制度风险不作考虑;3)内部风险和外部风险相对于总风险来说权重是相同的;4)系统风险不作考虑分析。
二、土地储备方案总风险的衡量
(一)风险评价指标的选取
为研究土地储备方案总风险的大小及其评价标准,选取内部风险中的盈亏平衡点、动态回收周期率(动态回收周期与土地持有期的比值)d、流动性风险(用银行贷款额和总投资的比值来衡量)l、财务内部收益率f以及外部风险中单位面积土地净收益率R、“内部收益率对土地收入的弹性”的绝对值r1、“内部收益率对开发成本的弹性”的绝对值r2等7个评价指标。
(二)研究思路
由于7个指标之间存在很强的相关性,如果直接进行综合评价,必然会造成信息的重复,影响评价结果的正确性。主成分分析方法可以把多个指标转化为少数几个不相关的综合指标,因此考虑利用主成分进行综合评价。1)依据所给数据求出内部风险评价指标和外部风险评估指标的具体值;2)运用Excel做出不同评估指标的折线图,将图中异于常值的数据进行剔除,同时为了消除单位因素的影响,对数据进行无量纲化处理;3)运用主成分分析法结合得到的数据,分别求出内部风险和外部风险关于相应评价指标的关系表达式;最后再运用层次分析法得到土地储备总风险关于评价指标的关系表达式。结构模型如图1所示。

图1 土地储备的总风险评估结构模型
(三)数据处理
运用Excel做出不同评估指标的折线图,将图中异于常值的数据进行剔除后,为了消除单位因素的影响,首先对各评价指标的值进行无量纲化处理[2]。
记原始矩阵为:
令
I1,I2,I3分别表示效益型、成本型和固定型指标集合。其中财务内部收益率、单位面积净收益均为效益型指标,盈亏平衡点、动态回收周期、流动性风险、“内部收益率对开发成本的弹性”的绝对值、“内部收益率对土地收入的弹性”的绝对值均为成本型指标,则无量纲后的矩阵为:
由于数据的庞大性,在此仅列举部分方案的数据无量纲化后的结果,如表1所示:
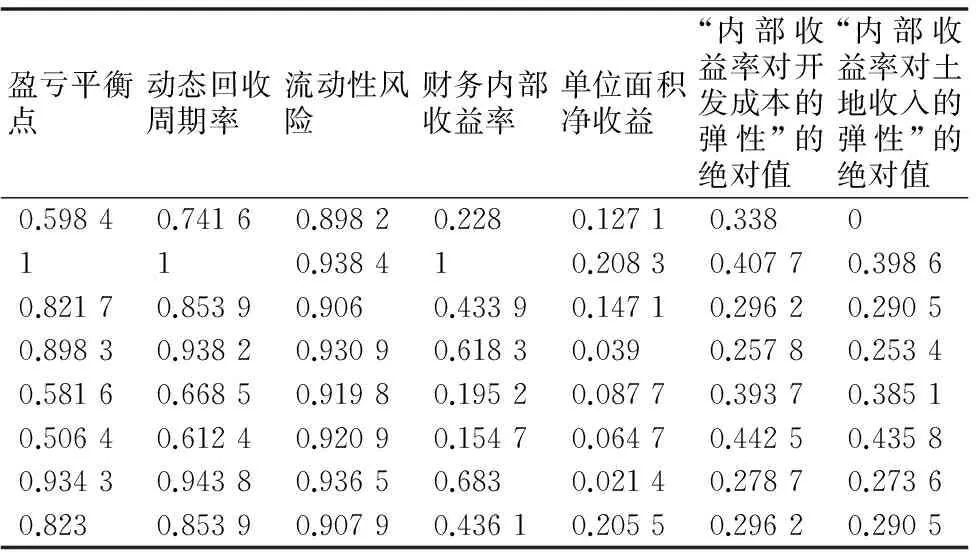
表1 部分方案风险评价指标的无量纲后的数值
(四)研究方法
经过模型的准备阶段、对数据的筛选与处理以及对土地储备风险与风险评价指标的初步分析,可得到土地储备总风险Y和风险评价指标之间的关系模型为:
Y=w1y+w2d+w3l+w4f+w5R+w6r1+w7r2
其中:w1,w2,w3,w4,w5,w6,w7为相应风险评价指标的系数。
使用主成分分析方法[3],在Matble编程中,运用eig命令,得到相应的风险评价指标的系数。同时得到最大的特征值的贡献率,以便判断使用此方法进行分析的有效性。
(五)结果分析
运用Matlab软件,求出前几个特征值及其贡献率,如表2所示:
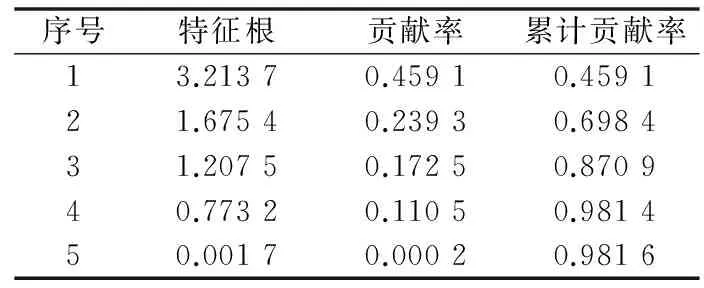
表2 主成分分析结果
可以看出,前4个特征值的累计贡献率就达到98.14%,主成分分析效果很好。因此选用前4个主成分进行综合评价。前4个特征值对应的特征向量如表3所示:
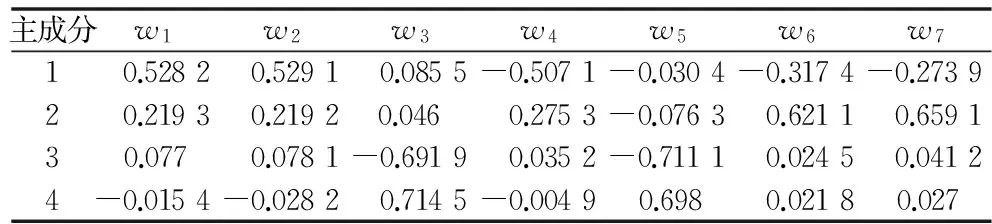
表3 前4个主成分对应的特征向量
分别以4个主成分的贡献率为权重,构建主成分综合评价模型,即:
Y=0.459 1y1+0.239 3y2+0.172 5y3+0.110 5y4
带入可得综合风险评价指标系数的值,如表4所示:

表4 风险评价指标系数
故土地储备总风险为:Y=0.336 6y+0.305 7d+
0.009 9l-0.161 4f-0.077 8R+0.009 5r1+0.042 1r2,且累计贡献率已达到98%以上。因此,利用主成分的得分来衡量土地储备总风险是有效的。
从定量角度出发,在本模型中的系数w1,w2,w3,w4,w5,w6,w7分别为7项风险评价指标对总风险的偏弹性。所谓偏弹性,即为当其他指标不变时,单一风险评价指标的变化对土地储备总风险的弹性。由上述分析可知:
1)盈亏平衡点对总风险的偏弹性为0.306 6,即当其他指标不发生改变时,盈亏平衡点每增加1%,则总风险的值会增加0.306 6%。
2)动态回收周期率对总风险的偏弹性为0.305 7,即当其他指标不发生改变时,动态回收周期率每增加1%,总风险的值就会增加0.305 7%。
3)流动性风险对总风险的偏弹性为0.009 9,即为当其他指标不变时,流动性风险的值每增加1%,则会使总风险的值增加0.009 9%。
4)财务内部收益率对总风险的偏弹性为-0.161 4,即当其他指标不改变时,财务内部收益率增加1%,则会使总风险下降0.161 4%,因此增加财务内部收益率能够有效降低风险。
5)单位面积净收益对总风险的偏弹性为-0.077 8,即单位面积收益每增加1%,总风险的值则会降低0.077 8%,因此提高单位面积净收益对降低总风险有很大的作用。
6)“内部收益率对土地收入的弹性”的绝对值对总风险的弹性为0.009 5,即当其他指标的值不变时,“内部收益率对土地收入的弹性”的绝对值每增加1%,会使总风险的值增加0.009 5%,因此增加项目的稳定性,减低“内部收益率对土地收入的弹性”的绝对值能够有效降低总风险水平。
7)“内部收益率对开发成本的弹性”的绝对值对总风险的偏弹性为0.042 1,即当其他指标的值不变时,“内部收益率对开发成本的弹性”的绝对值每增加1%,总风险的值增加0.042 1%。
从定性的角度来看,盈亏平衡点、动态回收周期率、流动性风险、“内部收益率对土地收入的弹性”的绝对值、“内部收益率对开发成本的弹性”的绝对值的增加会增加土地储备方案的总体风险。财务内部收益率和单位面积的净收益的增加会降低土地储备方案的总体风险。
三、土地储备方案总风险的评价标准
(一)研究思路
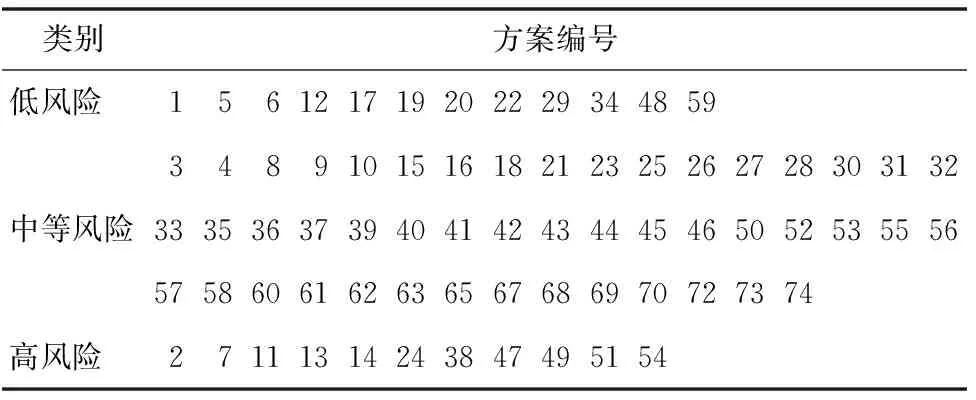
1)依据土地储备总风险和评价指标的关系表达式,可以计算得到不同项目方案的土地储备总风险的值并运用Matlab软件作出土地储备风险Y值的频数分布直方图。2)使用正态分布检验模型,对土地储备总风险Y值的频数分布进行正态分布检验。若土地储备总风险Y值服从均值为μ、方差为σ2的正态分布,则(Y-μ)/σ~N(0,1)。同时假设以方案的土地储备总风险Y值占总体土地储备总风险Y值较小20%的方案记为“低风险”,则低风险标准应满足p{(Y-μ)/σ (二)数据处理 由于数据过多,通过对不同方案的总风险的计算,得到部分不同方案的总风险,如表5所示: 表5 不同方案的总风险 表5 不同方案的总风险(续) (三)研究方法 利用Matlab软件的Hist命令做出总风险值得频数分布直方图,如图2所示: 图2 总风险的频数分布直方图 运用Matlab软件,使用Jbtest命令对总风险样本进行正态性检验。设标准值为H0,其检验标准为:若H0=0,接受原假设,即检验的样本服从正态分布;若H0=1,拒绝原假设,即接受备择假设,则检验样本不服从正态分布。经检验可知,总风险的样本标准值H0=0,故其符合正态分布。且总风险的样本的标准差为0.064,均值为0.444 2。低风险标准为Y≤μ-0.84σ=0.386 5,高风险标准为Y≥μ+0.84σ=0.494 1。 通过上述分析和对土地储备方案高、低、中等风险的假设可知:Y=0.306 6y+0.305 7d+0.099l-0.161 4f-0.077 8R+0.009 5r1+0.042 1r2 故当Y≤0.386 5时,可认为此时的土地储备方案的风险处在低风险区域;当0.386 5 表6 不同土地储备方案的总风险评价 综上所述,以上模型具有一定的合理性。选取对土地储备方案风险有影响的风险评价指标,再对大量的数据进行处理和分析,得到土地储备方案总风险与风险评价指标之间的关系为: Y=0.306 6y+0.305 7d+0.099l-0.161 4f-0.077 8R+0.009 5r1+0.042 1r2 故通过对风险评价指标的计算,就可以得到土地储备方案总风险的具体值,从而更加方便和准确地衡量一个土地储备方案总风险的大小。在此基础上,利用不同方案的土地储备方案总风险的值,运用正态分布检验和合理假设得到土地储备方案总风险的评价标准为: 本文所建立的模型,为衡量土地储备方案风险提供了参考,可通过对土地储备方案的风险评价指标的计算得到该方案的总体风险及其风险大小。 [1] 数学中国数学建模网络挑战赛组委会.2014年第七届“认证杯”数学中国数学建模网络挑战赛C题[EB/OL].[2014-07-20].http://www.tzmcm.cn/. [2] 吴礼斌,闫云侠.经济数学实验与建模[M].天津:天津教育出版社,2009. [3] 杨桂元,黄已立.数学建模[M].合肥:中国科学技术大学出版社,2008. [4] 杨桂元,朱家明.数学建模竞赛优秀论文评析[M].合肥:中国科技大学出版社,2013. [5] 潘春宏.土地储备风险控制研究[D].哈尔滨:哈尔滨工业大学,2009. [6] 陈云.土地储备的财务风险评价研究[D].雅安:四川农业大学,2011. Quantitative Land Reserve Risk Assessment Based on Principal Component Analysis ZHUJiaminga*,CHENGQianqianb,ZHUHailonga (a. School of Statistics and Appl. Math; b. School of Management Science & Industrial Engineering,Anhui University of Finance and Economics, Bengbu 233030, China) Aiming at the risk assessment for land reserve programs, the authors used Excel land reserve programs to screen and process related data, then employed the principal component analysis, fuzzy C-means clustering analysis and normality test methods to establish a land reserve program risk and other related evaluation model. Finally, Matlab programming was used to get total risk primarily through the establishment of risk assessment index to measure land reserve programs, and to establish appropriate risk assessment standard,at last, an effective approach for land reserve risk assessment was attained. land reserve; risk assessment index; cluster analysis; normality test; Matlab 2014-09-23 国家自然科学项目“随机动力系统的非一致指数二分性及其数值模拟”(11301001);安徽财经大学教研项目“数学建模竞赛引领大学生科研创新的研究”(acjyzd201429) 朱家明(1973— ),男(汉族),安徽泗县人,副教授,硕士,研究方向:应用数学与数学建模,通信作者邮箱:zhujm1973@163.com。 程倩倩(1993— ),女(汉族),安徽长丰人,在读本科生,研究方向:电子信息工程。 F301 A 2095-5383(2015)01-0022-04 10.13542/j.cnki.51-1747/tn.2015.01.006
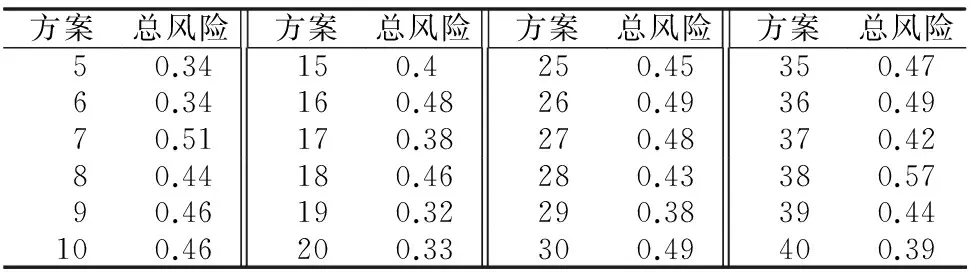
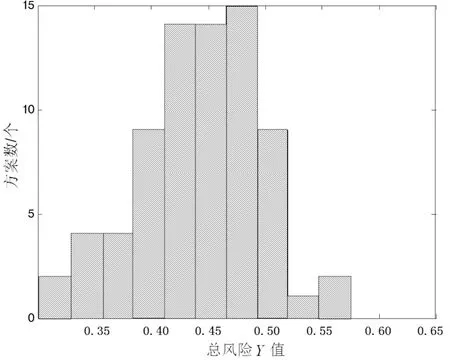
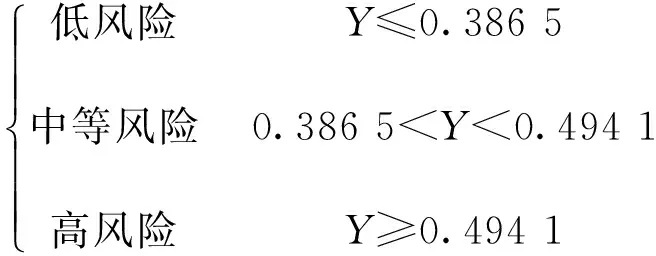
四、结语
