应用型本科院校大学生综合素质评价的实证研究

随国栋，陈华喜

(蚌埠学院 a.文学与教育系;b.数学与物理系，安徽 蚌埠 233030)

应用型本科院校大学生综合素质评价的实证研究

随国栋a*，陈华喜b

(蚌埠学院 a.文学与教育系;b.数学与物理系，安徽 蚌埠 233030)

为科学评判应用型本科院校大学生综合素质，采用改进三角模糊数的层次分析法对构建的大学生综合素质评价指标体系各指标进行赋权，然后利用模糊综合评判法构建一个大学生综合素质评价模型，进而运用该指标体系和评价方法进行实证研究，结果与实际情况基本一致。

应用型；大学生；综合素质；评价

大学生综合素质测评是结合在校大学生德、智、体、美等多方面做出的全面评价，它作为学校对学生评定奖学金和推荐就业的重要依据，是不断完善教学管理制度和培养人才的重要保障。本文在依据科学性、总体性以及层次性原则的基础上，结合相关部门专家的意见，构建一个应用型本科院校大学生综合素质评价指标体系(以下简称综合素质评价体系)，并采用基于改进三角模糊数的层次分析法对所建立的综合素质评价体系中的各级指标赋权，然后结合模糊综合评判法构建一个综合素质评价模型，进而结合实证研究，得出相关结论。

一、构建综合素质评价指标体系

建立包括德育(U1)、智育(U2)及体育(U3)3个一级指标在内包含13个二级指标的综合素质评价指标层次结构关系[1](如图1所示)，其中：1)德育指标包括人生观、价值观、社会公德以及人际关系4个二级指标。2)智育指标包括公共课、选修课、专业课、竞赛、过级以及专业实践6个二级指标。3)体育指标包括健康状况、体育成绩以及体育竞赛3个二级指标[2]。

图1 综合素质评价指标层次结构关系图

二、综合素质评价模型的建立

(一)设置综合素质评价指标体系

建立应用型本科院校大学生综合素质评价指标体系[3]，如表1所示。评价要素集合为U={U1,U2,U3}，各单要素的子集为U1={U11,U12,U13,U14}，U2={U21,U22,U23,U24,U25,U26}，U3={U31,U32,U33}。

表1 综合素质评价指标体系

(二)设定评语集合

将综合素质评价等级V[4]设置为5个等级，即V={v1,v2,v3,v4,v5}={一级，二级，三级，四级，五级}，对其赋值：V={95,85,75,65,55}，其中：级别越小表示综合素质越高。

(三)对指标体系中的各级指标赋权[5]

常见的确定权重的方法有：主观经验判断法、专家调查法或专家征询法、评判专家小组集体讨论投票法以及模糊层次分析法。本文采用改进三角模糊数的层次分析法赋权，步骤如下：

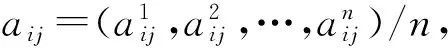
2．对上述A=(aij)n×n构造相应的模糊评判因子矩阵E，且

E(e)ij=

(1)

其中：Sij=(uij-lij)/2mij为折中后的离差率，也即标准离差率，Sij愈大，可信度就愈小，反之，若Sij愈小，则可信度愈大；

3.根据

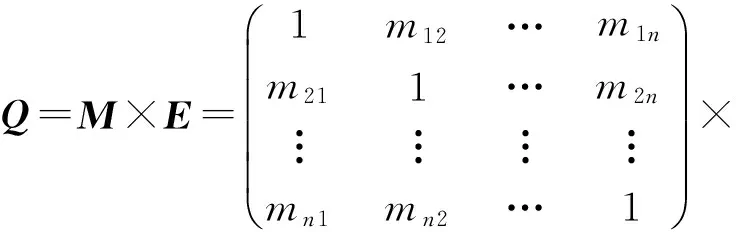
(2)

对评判因子矩阵E加以调整得到Q=(qij)n×n，其中：M是三角模糊判断矩阵A=(aij)n×n的中值构成的n阶矩阵；

4．利用

(3)

将Q变换主对角线元素均为1的判断矩阵A=(aij)n×n；

5．依据

(4)

将A=(aij)n×n转化为相容矩阵B=(bij)n×n，则B满足一致性的条件bij=bik×bkj，并有bii=1,bij=1/bji；

6．用

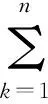
(5)

计算各指标在本层次中的权重wj，其中：

(6)

从而求得权向量W=(w1,w2,…,wn)。

(四)模糊综合评判的实施

2．根据文献[6]中的多级综合评判方法，可求出各子集评价决策矩阵，并最终求出综合素质的综合测评结果。

三、实例应用

提倡应用型本科教学模式是蚌埠学院近年来教学改革的重点方向，下面以蚌埠学院为例，对2012级学前教育专业某学生综合素质进行测评。

(一)确定各级指标的权重值

这里以一级指标体育(U3)的3个二级指标——健康状况(U31)、体育成绩(U32)、体育竞赛(U33)为例，说明权重的确定过程。

1．由专家根据各级指标间两两比较的结果，构造并得到的综合三角模糊判断矩阵

2．根据式(1)求得模糊评判因子矩阵

3．根据式(2)，计算调整判断矩阵

4．利用式(3)将Q转换为对角线为1的判断矩阵

5．由式(4)求得相容矩阵

6．由式(6)求出c1=1.11,c2=1.83,c3=0.49，再由式(5)得到一级指标体育的3个二级指标——健康状况(U31)、体育成绩(U32)、体育竞赛(U33)的权重分别w1=0.324,w2=0.533,w3=0.143，从而求得权向量WU3=(0.324,0.533,0.143)。

同理，可求得WU2=(0.305,0.223,0.234,0.238)，WU3=(0.168,0.199,0.257,0.117,0.159,0.100)以及WU=(0.423,0.331,0.246)，即表1括号内数值。

(二)综合评判的实施

组织10位相关专家按照5个等级对各二级指标进行投票，归一化[7]的结果见表1。则体育U3的权重向量

(0.2，0.5，0.3，0.3，0.1)

(三)评价得分

(四)结果分析

根据以上实证研究的过程及结果，可得如下结论：用模糊综合评价法[8]得出2012级学前教育专业学生综合评价结果是：20.8%为一级，28.5%为二级，18.4%为三级，18.4%为四级，13.9%为五级。根据最大隶属原则[9]，该学生综合素质评价等级为“二级”，综合得分为77.358，综合素质较高，结果与实际情况基本一致。

[1] 李真.适应社会需求的大学生综合素质测评体系的构建[J]．河北青年管理干部学院学报,2003(1):56-58.

[2] 刘新宪,朱道立.选择与判断:AHP(层次分析法)决策[M].上海:上海科学普及出版社,2004.

[3] 周义仓,赫孝良.数学建模实验[M].西安:西安交通大学出版社,1999.

[4] 杨启帆,李浙宁,王聚丰,等.数学建模案例集[M].北京：高等教育出版社，2003.

[5] 赵静，但琦.数学建模实验[M].2 版.北京：高等教育出版社,2003.

[6] 陈亚哲,刘桂珍,刘挺,等.基于熵权的产品广义质量模糊综合评价[J].东北大学学报(自然科学版),2010,31(2):241-244.

[7] 万远英,尹德志.大学生综合素质层次分析评价体系及其数学模型[J].西南民族大学学报(人文社科版),2003,24(12):191-193.

[8] 樊治平,姜艳萍,肖四汉.模糊判断矩阵的一致性及其性质[J].控制与决策,2006,16(1):69-71.

[9] 姜启源.数学模型[M].北京:高等教育出版社,1987.

Empirical Study on the Evaluation of Comprehensive Quality for Applied Type Undergraduate Colleges

SUIGuodonga*,CHENHuaxib

(a.Department of Literature and Education; b.Mathematics and Physics Department, Bengbu College, Bengbu 233030, China)

The comprehensive quality of college students has become the focus of attention of the state and society. For the undergraduate comprehensive quality evaluation for the universities of applied science , an improved analytic hierarchy process triangular fuzzy number is employed to weight each index on the construction of application oriented undergraduate college students comprehensive quality evaluation index system, and then the evaluation of an application type undergraduate college students comprehensive quality model is constructed using fuzzy comprehensive evaluation method, and at last, the index system and the evaluation method of empirical research are used. The result is consistent with the actual situation, the model has a certain value for practical use.

application; college student; comprehensive quality; evaluation

2014-06-18

安徽省高校优秀人才基金项目“质量工程背景下大学生素质耦合评价模型及算法研究”(2012SQRL216);蚌埠学院学生参与教师科研项目“应用型本科院校大学生综合素质评价模型的构建”(2013xsky07)；蚌埠学院教学研究项目“毕业生就业质量标准研究”(2013jyxm06)

随国栋(1991— ),男(汉族)，安徽太和人，助教，研究方向：统计分析，通信作者邮箱：bbxysgd@163.com。 陈华喜(1977— ),男(汉族)，安徽淮南人，副教授，硕士，研究方向：模糊统计。

G643.1

A

2095-5383(2015)01-0086-03

10.13542/j.cnki.51-1747/tn.2015.01.025