基于改进SLIC方法的彩色图像分割

张亚亚，刘小伟，刘福太，张建廷

(海军航空工程学院电子信息工程系，山东烟台264001)

1 概述

如何把目标物体从图像中有效地分割出来一直是计算机视觉和图像理解中的经典难题之一，它决定了图像的最终分析质量和模式识别的判别结果。图像分割是指将图像中具有特殊意义的不同区域分开，并使这些区域互不相交，每个区域满足特定区域的一致性条件。图像分割中尺度问题是图像处理一直关注的重点，传统的基于像元的方法都是在一个尺度上分析的，当要同时描述、解释或提取几个尺度的地物类型时，单一尺度的数据往往不能解决问题。目前，较流行的超像素方法，利用尺度思想将图像过分割生成多个同质性区域，它捕捉图像的冗余，更有利于从中计算图像特征，并降低了后续图像处理的复杂程度。因此，基于超像素［1］的图像分割方法以其良好的分割边界［2］、高效处理速度及较低的计算复杂度［3］，广泛应用于图像分割预处理过程中。

目前，产生超像素的方法主要分成2类:基于图论的方法和基于梯度上升的方法［4］。基于梯度上升的分割方法首先得到一个粗略聚类，利用梯度上升的方法改进前一次迭代聚类的结果，直到收敛。基于梯度上升的方法主要有均值漂移(Mean Shift)［4］、快速漂移(Quick Shift)［5］及简单线性迭代聚类(Simple Linear Iterative Clustering，SLIC)［6］等。基于图论的方法把图像分割问题关联到最小割问题，将图像映射为带权的无向图，图中每个节点对应于图像每个像素，边权值表示相邻像素间相似度，分割的最优原则是类内间相似度最大，类类间相异度最大。基于图论的分割方法主要有归一化分割［7］、基于图的分割［8］、图分割［9］等。Mean Shift一个迭代的模式搜索程序，目的是定位找到密度函数的局部最大值，通过转换后能应用于模式识别中图像的颜色或亮度的特征空间，聚集到相同模式的像素群能定义为超像素。快速漂移也是利用模式搜索的分割思想，具有可控制的模态选择和平衡“过分割”与“欠分割”的特点，它利用一个Medoid Shift程序来初始化分割，然后将其移至每个点在特征空间中的最近邻域，增加了Parzen密度估计，其优点是不需要迭代，但它不能固定产生超像素的形状和数量，且紧凑程度较差。归一化分割是典型的基于图论的方法，它利用轮廓特征和纹理特征将一幅图像中所有像素点组成的图形反复分割，在分割边界的边缘上限定一个惩罚函数，产生的超像素非常规律，可视效果较好。缺点是边界命中率较差，分割速度相当慢。基于图的分割是基于图节点聚类，它将生长树中路径最短的节点归为同一类聚集成超像素。优点是速度较快、复杂度低，但是不能合理控制超像素的数目。

文献［7］分析比较了各种生成超像素方法，得出生成超像素的最优方法是SLIC方法，该方法通过改进K均值聚类的方法，用LAB颜色空间及x，y像素坐标对像素进行聚类，有效生成具有较好的紧凑性和高精度分割边界的超像素，且此方法能灵活控制超像素数量，运行速度快，只需要线性运行时间和内存，有效提高了分割方法的性能。但此方法中存在这样一个问题:在K均值迭代聚类方法中，若某次迭代时出现像素错误分类，在之后的迭代过程中就会复制错误点，最终形成错误的超像素。由于聚类方法条件有限，形成了许多小区域的超像素块，并且小超像素块也并非完全会包含边界信息，因此如何减少迭代过程中的错误分类，较小区域块的超像素合并区域成为影响分割准确度的重要因素之一。

本文针对SLIC方法中存在的不足，提出一种基于改进SLIC方法的遥感图像分割方法。利用非线性扩散滤波器的保边优点，对图像进行滤波，去除图像的琐碎细节，减少噪声且有效保留边界，通过Sigma滤波器改进SLIC方法，对图像在颜色和距离空间内完成聚类，获得分割结果，并进行仿真实验。

2 图像平滑

在运用SLIC方法对图像进行分割时，由于方法条件有限，在图像细节区域会产生大量微小区域，而这些区域的存在会大大影响区域合并过程的速度及图像分割效果，因此在对图像进行初始分割前，有必要对图像进行滤波处理，在平滑图像和抑制噪声的同时有效地保留边界。考虑利用目前边缘保持效果较好的非线性扩散滤波器［10］，非线性扩散技术是考虑图像中不连续部分(边缘、轮廓等)的一种平滑技术，它在运算过程中考虑到图像的边缘和非边缘区域的区别，采用不同的平滑策略，从而获得不同的扩散效果。

含噪声图像模型如下:

其中，u为真实场景的清晰图像;u0为u的一个观测;n为噪声。针对上述模型，其边界条件和初始条件表示为:

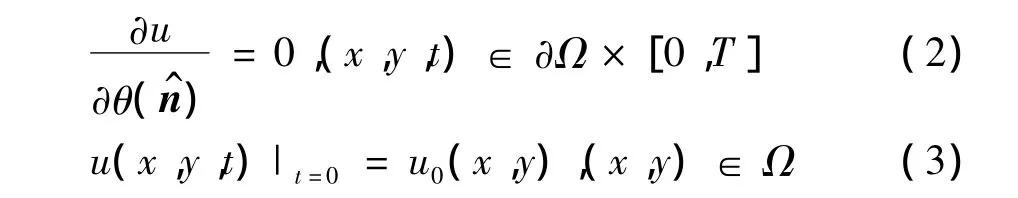
一般的非线性扩散方程表达式如下:

其中，α =α(x，y，t);β =β(x，y，t)为系数。

选取Sochen非线性扩散方程［11］进行求解:

系数表达式模型可表示为:

对于式(4)有k=1，k为正参数。在区域内部，有▽u→0，αβ→1;在边缘附近，▽u→∞，αβ→0。在梯度较小区域，通过CFL条件进行均值平滑［10］，在边缘附近，梯度较大，保留清晰边界，不进行任何滤波。

3 SLIC方法及其改进

传统K均值聚类是一种非监督实时聚类方法，基本思想是在最小误差函数的基础上将数据划分为预定的类数K，方法的运算过程是:先指定类数K，K个初始聚类中心初值、迭代次数或收敛条件等，然后根据一定的相似性度量准则，将每一个数据分配到最近或“相似”的聚类中心，形成类，再以每一类的平均矢量作为这一类的聚类中心，进行重新分配，通过反复迭代直到达到最大的迭代次数。其优点是时间复杂度低，在处理大型数据集时，具有相对伸缩性和高效性，对较密集区域且区域间区别明显时分割结果较好。但是其缺点是无法克服的，即K均值方法聚类结果易局部收敛，对初始聚类中心选择有很强的依赖性，若选取不当，将造成无法挽回的后果，K均值方法需要事先给定聚类类数K，而人为设定，无法避免主观因素的影响，由于只考虑像素颜色距离，因此对噪声和孤立点数据非常敏感，且只能用于均值被定义的数据集，不应用与大小差别大的类。SLIC方法是对K均值聚类的改进，克服了上述类似问题的出现。

3．1 SLIC 方法

SLIC方法是通过改进传统K均值方法，即考虑像素的颜色信息又充分利用像素的空间信息，将颜色相似、图像空间距离接近的像素点聚集在一起的一种高效方法。在CIELAB颜色图像空间存在2个特征向量:像素 i彩色值 Ci=［Li，ai，bi］和在二维空间中位置 Si=［xi，yi］T。

采用新的距离度量方法改进超像素的形状，与一般特征空间欧式距离有所不同，SLIC方法克服了传统欧式距离在当空间上点超越颜色距离极限时偏向于像素颜色的相似性，所导致的超像素不再考虑区域边界的问题。k从初始聚类中心 Ci=［li，ai，bi，xi，yi］T开始均匀地采样，为避免出现超像素中心在边界位置及噪声像素冒充种子像素的现象，将聚类中心限定在最低梯度量的3×3邻域内移动，每一个像素通过与最近邻聚类中心距离D来进行聚类，具体如下:

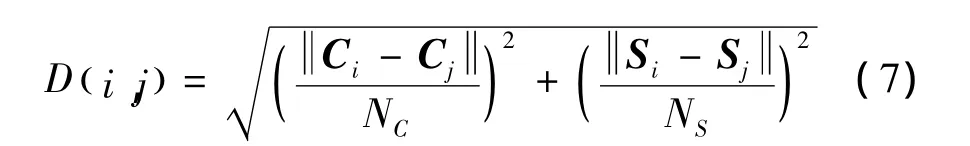
其中，j是聚类中心下标，j=1，2，…，K;Nc和 Ns分别为彩色和空间距离的归一化常数，一旦像素聚集到最近邻的中心像素后，更新中心φ，代替聚类中所有像素平均向量:

其中，Gj表示在φj位置的聚类区域;N表示在Gj内所包含的像素数量。

然而上述SLIC方法处理第一步迭代后的图像没有特别强调像素间的联通性，结果可能会形成许多小的、孤立的分割点。而对于最后一步迭代后孤立的点，SLIC形成形状、大小一致的超像素作为下一步的应用，将孤立点无限制地归为孤立点所在位置的最大邻域内，显然这种做法对分割结果准确率是有很大影响的。

3．2 改进的SLIC方法

针对SLIC方法存在的问题，利用Sigma滤波器［12］来避免过多的错误迭代。传统 Sigma滤波器［13］是建立在假设窗口内像素灰度值与其中心像素的灰度值比较接近的基础上的，将滑动窗口中与中心像素偏差小于2δ的所有像素取平均，并设置平均像素的限制条件以滤除孤立的噪声点。因此，在第一次迭代后，设定条件假设窗口内像素的矢量值与其中心像素的矢量在αδ范围内，满足这个条件方能更新聚类中心模型，若不符合相似条件，则不能合并，需要寻找另一个与之亮度值相似的聚类中心，方能完成聚类。

取Gj范围内所有像素点的彩色矢量为 C1，C2，…，CN，首先计算它们的均值:

其中，δ表示在Gj内所有样本像素彩色的标准偏差;α为常数;φ为更新后的聚类中心，通过此方法的迭代更新，改变了原来聚类时出现的错误，增加限定条件使得后期迭代更新、聚类过程更准确。

通过上述方法，对迭代前可能出现的错误进行了修正。但是对于最后一步迭代后孤立的点，由于过度考虑超像素大小必须一致，SLIC将它们的标签归为与之最近的聚类中心上，这种做法没有充分考虑当前孤立点与它最近邻最大集群间的相似性，结果将导致生成的超像素不能有较好的图像边界。考虑增加条件利用两集群间亮度的相似性衡量合并标准来代替相邻集群间的尺寸关系［14］，条件如下:

其中，Dm表示最小的集群G和它最近邻最大集群Gm亮度距离，m=1，2，…，M;μ 和 μm分别表示最小集群平均亮度值和它最近邻集群的平均亮度值;Ds表示 Dm最小值 min(Dm)，s∈［1，M］，当 Ds＜T 时，最小集群Ds合并到它在s处的邻域Gs内;否则，这个最小集群继续寻找最相近的区域进行合并。

改进SLIC方法步骤如下:

(2)将聚类中心点移至3×3邻域内的最低梯度位置。

(3)对每个聚类中心Ck的2S×2S邻域，计算每个像素i到中心Ck的空间距离D，在更新聚类中心过程中加入条件式(13)。

(4)若D＜d(i)且彩色距离在归定范围内，则将为D的值赋值给 d(i)，通过标签记录此时的位置。

(5)反复执行步骤(3)和步骤(4)，计算新的聚类中心和残余误差E，直到达到设定阈值。

(6)初步迭代结束后，利用条件式(14)中Dm合并孤立点，完成分割。

4 实验结果与分析

本节使用一系列纹理和彩色信息丰富的自然彩色图像进行实验，比较分析本文方法在各个方面相对于SLIC的性能优势。所有实验图像来源于Berkeley自然图像库。实验平台为 Inter Core i5 CPU 760 2．8 GHz主频和4 GB内存。改进算法步骤如下:

第1步非线性滤波

滤波器参数设置如下:(1)最大迭代次数，本文实验滤波迭代次数取为20，超过最大迭代次数滤波器效力不明显，造成时间浪费，若迭代次数过小，滤波效果也不理想;(2)步长设置，滤波器步长取值影响保边效果程度，受CFL条件［15］限制，实验观察选取步长为0．1;(3)滤波尺度，滤波尺度用于控制平滑程度，过大容易模糊必要细节，过小滤波效果不明显，本文实验滤波尺度设置为1．6。

第2步超像素分割

参数设置如下:(1)迭代最大次数，本文实验控制迭代次数为10，迭代次数过大聚类达到饱和、浪费时间、迭代次数过小、聚类效果不理想;(2)超像素个数(超像素个数=图像全部像素个数∕每个超像素包含的像素个数)，本文实验将原方法与改进方法的超像素个数均设为K=400，超像素个数过多、过分割现象较严重，且不能体现超像素的高效率特点、超像素个数过少、边界分割易出现错误;(3)紧致度，紧致度用于控制超像素形状，紧致度越大，超像素形状更规则、统一，但超过某一临界值会忽略某些边界，过小则造成超像素较杂乱、无规则。为了使生成的超像素大小更均匀，且形状更规则，本文取 Compactness=40合适;(4)在式(13)中，α影响迭代更新聚类的准确度，本文实验α=5，若α增大，孤立点增多。

本文重点列出了3组图像(来自Berkely分割数据库)的分割结果图并进行放大分析。如图1所示，图1(b)平滑后帽子和头发等多余纹理得到消除，而边界保留效果较好;图1(c)中原方法阴影分割到帽子区域中;图1(d)中本文方法将帽子和阴影清晰分割;图1(e)中通过平滑再用本文方法分割，形成的超像素块大小均匀，帽子、阴影头发的边界都分割出来。如图2所示，图2(b)平滑后小船的轮廓更加清晰;图2(c)中原方法小船的船头部分被合并到水中;图2(d)中本文方法将船头与水面清晰分割出来;图2(e)中既将船头与水面边界分割出来，且超像素大小形状更规则。如图3所示，图3(b)通过平滑后山坡和树叶纹理得到消除，山坡和树叶边界更清晰;图3(c)原方法中模糊了树叶和天空的边界，塔顶与山坡边界也不清晰;图3(d)本文方法将树叶边界与天空分割出来，但山顶一小部分还需完善;图3(e)平滑后在处理将树叶与天空、山坡等边界都分割出来。

图1 BSD-15004分割结果比较

图2 BSD-145079分割结果比较

图3 BSD-126007分割结果比较

如表1所示，原方法和本文方法对上述3幅图片的程序处理时间，对比发现，在结果可视分割效果较好的基础上，本文方法并没有过大增加时间复杂度。

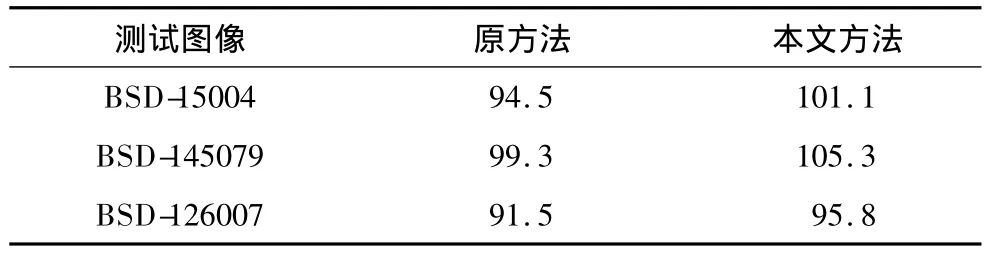
表1 程序处理时间比较 10－3s

如图4所示，对Berkeley数据库中300幅321×481像素的图像进行处理，利用原方法、本文方法及平滑后本文方法的分割结果分别与BSD中分割真值图对比的边界命中率统计结果，从图中可以看到，随着超像素个数的增加，相比原方法，本文方法边界命中率斜率更大、分割命中率也更高。由于利用非线性滤波器平滑图像后起到了锐化图像边界的效果，因此边界命中率也更高。当超像素数量达到一定时，3种方法边界命中率趋于平稳。

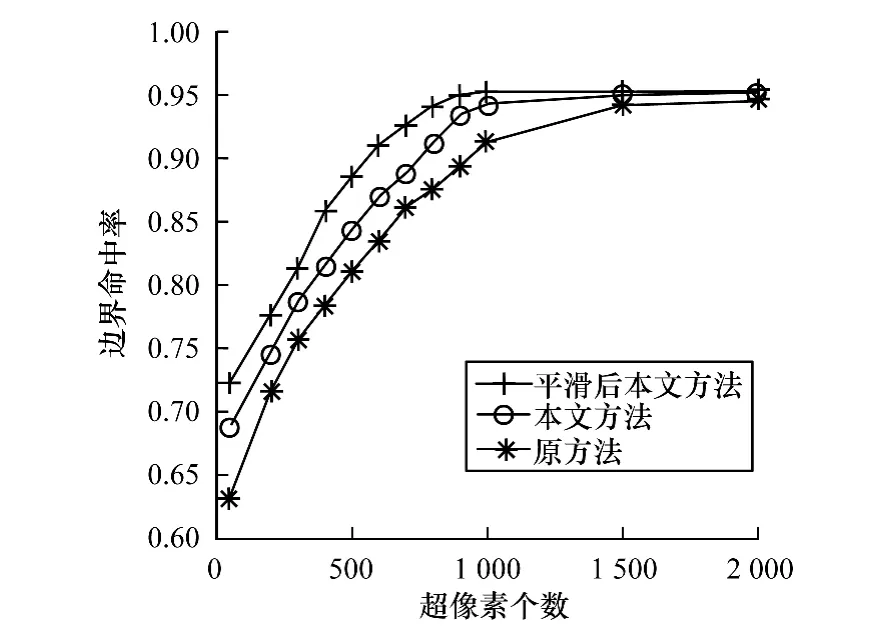
图4 边界命中率对比

以上实验结果分别从可视分割效果、时间复杂度和边界命中率3个方面进行分析得出，本文方法对于纹理和色彩边界不明显的区域比原方法分割效果更好，本文通过在迭代的过程中重新计算距离进行分割聚类，在增加分割效果的同时处理时间没有太大增加，利用非线性滤波器平滑图像内部的多余纹理区域，对边界部分保留较好，并在此基础上进行分割，结果产生的超像素形状大小和分割可视效果较好。边界命中率是图像分割边界准确度的重要判断依据，直接影响了分割精度，本文方法的边界命中率比原方法更高，说明本文方法处理结果更具优势。

5 结束语

本文提出一种改进的SLIC方法。利用非线性滤波去除多余纹理，且保持较好的图像边界，结合Sigma滤波器特性增加聚类限定条件。实验结果表明，与原方法相比，该方法的分割精确度有所提高。如何将超像素的方法应用到复杂遥感图像处理中，进一步提高分割效率和精度，减少计算复杂度，是今后的研究重点。

［1］ 王春瑶，陈俊周，李 炜．超像素分割算法研究综述［J］．计算机应用研究，2014，31(1):6-12．

［2］ Xiang Deliang，Tang Tao，Zhao Lingjun，et al．SuperpixelGenerating Algorithm Based on Pixel Intensity and Location Similarity forSAR Image Classification［J］．Geoscience and Remote Sensing Litters，2013，10(6):1414-1418．

［3］ 谭乐怡，王守觉．基于双重超像素集的快速路径相似度图像分割算法［J］．自动化学报，2013，39(10):1653-1664．

［4］ 饶 倩，文 红，喻 文，等．超像素及其应用综述［J］．电脑与信息技术，2013，21(5):1-3．

［5］ Comaniciu D，Meer P．Mean Shift:A Robust Approach Toward Feature Space Analysis［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(5):603-619．

［6］ Vedaldi A，Soatto S．Quick Shift and Kernel Methods for Mode Seeking［C］//Proceedings of ECCV’08．Berlin，Germany:Springer-Verlag，2008:705-718．

［7］ Achanta R，Shaji A，Smith K，et al．SLIC Superpixels Compared to State-of-the-art Superpixel Methods［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34(11):2274-2281．

［8］ Shi Jianbo，Malik J．Normalized Cuts and Image Segmentation［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(8):888-905．

［9］ Felzenszwalb P F，Huttenlocher D P．Efficient Graphbased Image Segmentation［J］．International Journal of Computer Vision，2004，59(2):167-181．

［10］ Li X，Sahbi H．Superpixel-based Object Class Segmentation Using ConditionalRandom Fields［C］//Proceedings of IEEE International Conference on Acoustics，Speech and Signal Processing．Washington D．C．，USA:IEEE Press，2011:1101-1104．

［11］ 姚 伟，孙即祥．保护角点的非线性扩散滤波［J］．中国图象图形学报，2010，15(4):577-581．

［12］ Sochen N，Kimmel R，Malladi R．A General Framework for Low Level Vision［J］．IEEE Transactions on Image Processing，1998，7(3):310-318．

［13］ Lukac R，Smolka B，Plataniotis K N，et al．Vector Sigma Filters for Noise Detection and Removal in Color Images［J］．Journal of Visual Communication and Image Representation，2006，17(1):1-26．

［14］ Lee J S．DigitalImage Smoothing and the Sigma Filter［J］． Computer Vision Graphics and Image Progress，1983，24(2):255-269．

［15］ Kim K S，ZhangDongni，KangMun-Cheon，et al．Improved SimpleLinearIterativeClustering Superpixels［C］//Proceedings of the 17th IEEE International Symposium on Consumer Electronics．Washington D．C．，USA:IEEE Press，2013:259-260．