基于垂直平分线的无线传感器网络定位改进算法

董海棠，万国峰，骆岩红

(1．兰州交通大学机电工程学院，兰州730070;2．西北民族大学电气工程学院，兰州730030)

1 概述

无线传感器网络(Wireless Sensor Network，WSN)通常利用已知坐标位置的信标节点去推算其余未知目标节点的位置坐标［1-2］，因此产生了很多定位算法。其中，研究和应用最广泛的当属质心算法［3］。质心算法的定位精度受网络节点分布和锚节点位置影响较大，尤其当锚节点所接收的信息的方差很大时，定位精度就会变得很低［4］。接收信号强度指示(Received Signal Strength Indication，RSSI)距离测量无需额外硬件，实现简单，具备低功耗、低成本等特点，应用十分广泛［5］。文献［6］等将RSSI与质心算法相结合，得到多种基于RSSI的加权质心定位算法，定位精度有所提高，但当参与定位的锚节点构成的多边形比较扁平或分布在区域中心时，定位覆盖率较低。文献［7］提出了基于三角形角度的加权质心算法，能较好地解决这个问题。而文献［8］用粒子群优化的方法，文献［9］用遗传算法，文献［10］用模拟退火算法提高定位精度。

为克服基于单跳的定位算法因为参与定位的锚节点初始坐标相同而使可计算的有效节点数目减少，未知节点最终无法进行定位求精的缺点，文献［11］提出基于跳数的无线传感器网络定位求精算法。

前面提到的算法有的定位精度很低，有的计算量和通信开销大，且都存在定位覆盖率不够高的缺点。为此，文献［12］提出基于区域的无需测距的APIT定位算法，但该算法一方面通信开销大，另一方面定位覆盖率很低。文献［13］提出的基于垂直平分线的区域定位算法(Midnormel-based area Location Algorithm，MBLA)和文献［14］提出的 IAPIT算法(Improved Approximate PIT Test)力图分别解决上述2个问题。

在文献［15］提出的无线电传播对数路径损耗模型基础上，文献［16］提出了基于参考锚节点的高斯校正模型(Reference-Gauss)。运用高斯分布函数处理未知节点收集到的n个从同一个发送节点发出的RSSI值，滤除概率密度小于0．6的RSSI值，然后求剩余的平均值，得到最终的优化RSSI值。不但消除了小概率事件对测量值造成的误差，而且消除了环境散逸因子的影响，适合各种环境下的RSSI值测距。本文运用这一理论进行测距，根据待定位节点接收到的2个锚节点RSSI值的比值，将定位区域分割，以提高定位精度，降低迭代次数。同时为防止恶意攻击，还提出防攻击模型。

2 相关工作

2．1 IAPIT 算法

IAPIT算法是将三边测量法以及几何上的由已知两点在辅助条件下求解两圆交点的方法与APIT算法相结合，对于不能用APIT定位的节点，当与其通信的锚节点数为3个及以上时，用三边测量法定位，等于2个时，以两锚节点为圆心，通信距离为半径作圆，两圆的相交部分的几何中心就是节点的估计位置。这一算法存在2个缺点:(1)算法复杂;(2)仍有无法定位的节点，说明定位覆盖率还是不够。

2．2 MBLA 算法

MBLA算法的核心思想是在与待定位节点能通信的锚节点集合中任意选择2个，这2个锚节点连线的垂直平分线把整个区域分成两部分。比较待定位节点与这两个锚点的信号强度，则待定位节点一定位于信号强度强的锚点驻留的一侧。在图1中，待定位节点一定位于垂直平分线的a侧。

图1 MBLA判定原理

显然，如果用该算法，每次定位的范围比较大，定位精度不够高，要达到要求的定位精度，需要迭代的次数较多，节点能量消耗大，不适合能量受限的无线传感器网络。

为解决传统算法定位精度低、算法复杂、迭代次数多、消耗能量多等缺点，本文提出以待定位节点接收到的2个锚节点的RSSI值的比值为权值的改进垂直平分线定位算法(Improved Midnormal-based Localization Algorithm，IMBLA)。

3 IMBLA算法

IMBLA算法根据未知节点接收到的两锚节点的RSSI值的比值，移动两锚点的垂直平分线，然后确定待定位节点位置在移动后的垂直平分线的哪一侧。

3．1 算法描述

3．1．1 理想情况下的IMBLA算法

IMBLA在可与之通信的锚点集合中以数学上排列组合的方式选择2个锚点，则未知节点与锚点的关系一般为图2所示的情况。

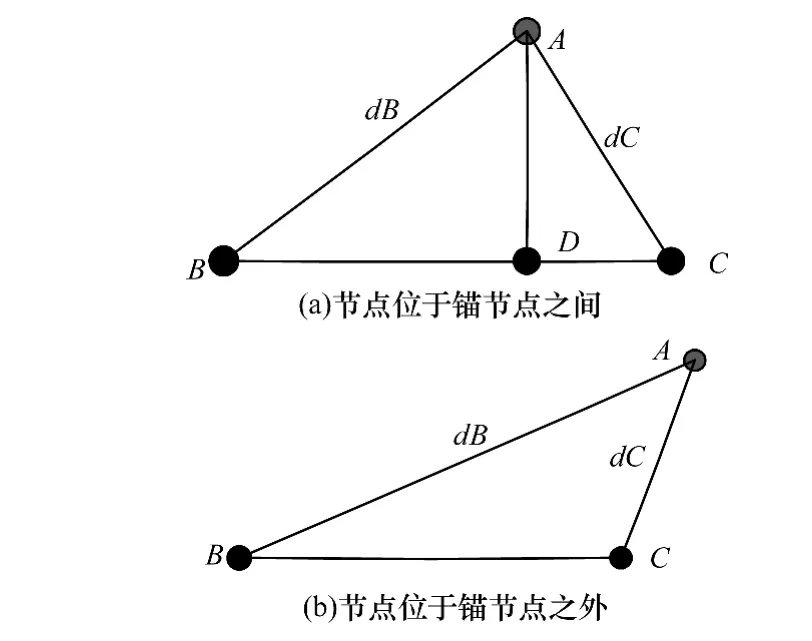
图2 定位情况

对于满足式(1)的情况，以 B点为基点，按dB/(dB+dC)比例对BC做垂线，这样把整个区域分成两部分，则可以肯定未知节点在锚节点C所在的这部分区域。

若满足式(2)，则将BC的垂直平分线移动到C点，未知节点一定在B点的对侧区域。

整个定位过程就是不断地重复这个判定过程，每一次判定都会缩小待定位节点可能的所在区域，直到所有的锚节点穷尽，或定位精度已达到所需精度，则算法结束。

3．1．2 非理想情况下的IMBLA算法

假设所有节点都布置在X-Y平面，如图3(a)所示的节点Ni和Nj分别以角pij和pji相互能看见，两点之间的距离为dij。那么节点Nj相对于Ni的坐标为 xij=dijcospij和 yij=dijsinpij，同理，节点 Ni相对于 Nj的坐标 xji=dijcospji和 yji=dijsinpji。如果距离和角度的测量没有误差，则(xij+xji)=0，(yij+yji)=0。

当有障碍物时，由于多径传播，一个待定位节点可能会接收到一个锚点的多个RSSI值，如图3(b)所示。节点Ni看到的节点Nj有2个位置(xij，yij)和(x'ij，y'ij)，其 RSSI值也不同，分别是 RSSIij和 RSSI'ij。同理，节点Nj看到的节点Ni也有2个坐标(xji，yji)和(x'ji，y'ji)。

图3 定位误差监测图

显然，(xij+xji)和(yij+yji)的值最小者为节点Nj相对于节点Ni的真实位置，即满足式(3):

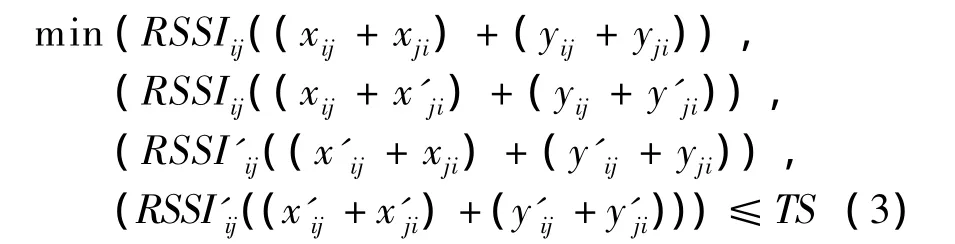
其中，TS是事先给定的误差阈值。

3．1．3 算法对恶意攻击的应对

所有节点与其相邻节点交换信息，对于符合式(3)的节点，给可信任标志值，而对超过阈值TS的节点，给不可信任标志。当节点受到攻击时(不论内部攻击还是外部攻击)，将不符合式(3)，则这样的节点就是不可信任节点，不能参与定位，从而避免了恶意攻击对算法的影响。由于该算法是基于区域定位的算法，显然在防止恶意攻击方面要比质心算法等优越。

3．2 算法步骤

算法步骤如下:

(1)各个锚节点周期性地向周围广播自身节点ID和位置。

(2)未知节点则收到与其能通信的锚节点的信息，从而构成各自的锚节点集合，并根据接收到的锚节点的RSSI值确定其与锚点之间的距离。

(3)在该锚点集合中用排列组合方式取2个点，与待定位节点构成图2。用余弦定理判定∠ACB的大小，若小于，则按dB/(dB+dC)的比例作BC的垂线，把区域分成2个区域，未知节点就在锚点C所在的区域，否则，在对侧区域。若满足式(2)，则通过C点作BC的垂线，把区域分成2个区域，未知节点就在B点的对侧区域。

(4)若定位精度未达到要求或还有锚节点组合没有被测试，则重复步骤(3)，否则执行步骤(5)。

(5)计算重叠区域的重心(若已经达到定位精度，则此步骤不用)。

4 仿真结果

在Matlab7．10环境下进行仿真。节点通信半径为R;节点随机布置在一个5R×5R的正方形区域内。

定位误差计算公式如下:

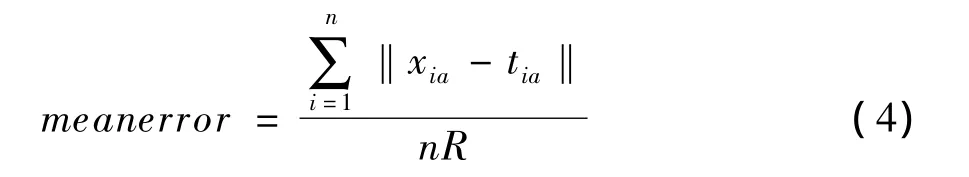
其中，xia和tia分别是未知节点的估计坐标和实际坐标。

4．1 迭代次数对定位误差的影响

设总共有200个节点，其中锚节点占15%，所有节点通信半径 R=10 m，MBLA和 IMBLA及IAPIT3种算法的仿真结果如图4所示。可以看出，IAPIT的误差比较大，其最小误差略小于1 m;MBLA进行17次迭代后误差减小到0．5 m，而IMBLA算法只用了4次迭代，误差就降到0．5 m以下，最终接近0．25 m。迭代次数的减少能有效减小节点能量消耗，对于能量受限的无线传感器网络具有较大的意义。

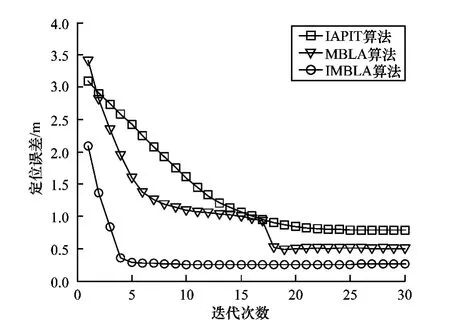
图4 定位误差与迭代次数的关系

4．2 定位误差率与可通信锚节点比例的关系

总节点数不变，改变锚节点的比例，对3种算法进行仿真，得出定位误差率(定位误与通信半径之比)与锚节点比例的关系，结果如图5所示。

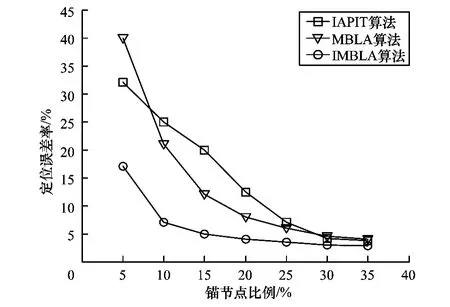
图5 定位误差率与锚节点比例的关系

由图5可知，锚节点比例在5%以下时，IMBLA算法的定位误差率是MBLA的1/3左右，其原因是MBLA是以锚节点连线的垂直平分线划分区域，当锚节点数量比较少时，区域划分粗略，待定位节点可能的位置的范围大，而IMBLA是根据接收到的锚节点的信号强度的大小把区域划分成两部分，区域划分比较精细，有效缩小了待定位节点所在的范围，误差率大大减小。锚节点比例增加到10%以后，IMBLA的定位误差率在10%以下，另两种算法的定位误差率还在20%以上。随着锚节点比例的逐渐增加，划分的区域越来越小，MBLA算法的定位精度逐渐接近IMBLA的定位精度。IAPIT算法的定位误差率比前两种算法大，当锚节点比例为15%时，误差率是IMBLA的4倍，是MBLA的2倍，不过，定位精度也随锚节点的增加而逐渐提高。锚节点比例达到35%以后，三者的定位精度接近。

4．3 网络的定位覆盖程度

图6是在锚节点比例变化下，3种算法中可定位节点数的比较。当锚节点比例为5%时3种算法的定位覆盖率(能够定位的节点数与总节点数之比)基本一样，都很低。随着锚节点比例的增加，IAPIT算法定位覆盖率上升缓慢，IMBLA和MBLA算法都迅速上升，但前者的定位覆盖率明显比后者高。锚节点比例上升到35%后，IMBLA算法的定位覆盖率接近100%，另两种算法的定位覆盖率则分别是90%和87%。

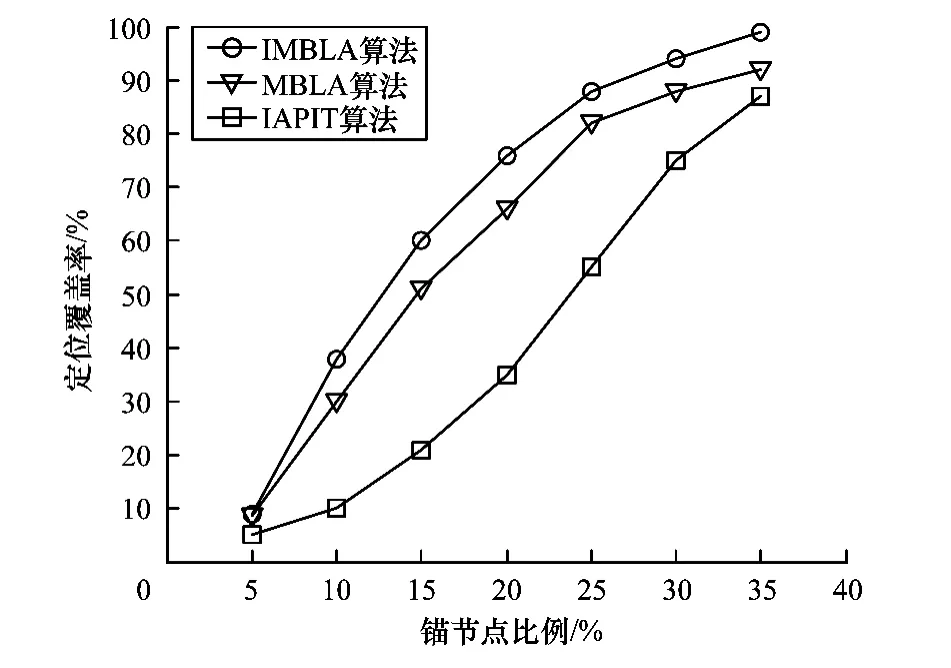
图6 定位覆盖率与锚节点比例的关系

5 结束语

本文在分析MLBA算法、APIT算法和IAPIT算法优缺点的基础上，借鉴加权质心算法，提出了MLBA算法的改进算法IMBLA。仿真结果表明，与MBLA和IAPIT算法相比，该算法定位精度和网络覆盖率较高，但其缺点是算法复杂度比MLBA高，虽然迭代次数比 MLBA少，但每次迭代耗时较MLBA高，因此，下一步将就此做一步改进。

［1］ Liu Yunhao，Yang Zheng，Wang Xiaoping．Location，Localization，and Localizability［J］．Journal of Computer Science and Technology，2010，25(2):274-297．

［2］ Yang Zheng，Liu Yunhao．Quality ofTrilateration:Confidence-based Iterative Localization［J］．IEEE Transactions on Parallel and Distributed Systems，2010，21(5):631-640．

［3］ Bulusu N，Heidemann J，Estrin D．GPS-less Low Cost Outdoor Localization for Very Small Devices［J］．IEEE Personal Communications Magazine，2000，7(5):28-34．

［4］ 刘运杰，金明录，崔承毅．基于RSSI的无线传感器网络修正加权定位算法［J］．传感技术学报，2010，23(5):717-721．

［5］ Zhong Ziguo，He Tian．Achieving Range-free Localization Beyond Connectivity［C］//Proceedings of the 7th International Conference on Embedded Net-worked Sensor Systems．New York，USA:ACM Press，2009:281-294．

［6］ 花 超，吉小军，蔡 萍，等．基于RSSI差分修正的加权质心定位算法［J］．传感器与微系统，2012，31(5):139-144．

［7］ 刘 瑾．基于测距的无线传感器网络的定位算法的研究［J］．航空计算技术，2009，39(6):124-126．

［8］ 王新芳，张 冰，冯友兵．基于粒子群优化的改进加权知心定位算法［J］．计算机工程，2012，38(1):90-95．

［9］ 章 磊，段莉莉，钱紫鹃，等．基于遗传算法的WSN节点定位技术［J］．计算机工程，2010，36(10):85-87．

［10］ Kannan A A，MaoGuoqiang，VuceticB．Simulated Annealing Based Localization in Wireless Sensor Network Localization with Flip Ambiguity Mitigation［C］//Proceedings ofthe 63rd IEEE Vehicular Technology Conference．Washington D．C．，USA:IEEE Press，2006:1022-1026．

［11］ 郭永红，万江文，于 宁，等．基于跳数的无线传感器网络定位求精算法［J］．计算机工程，2009，35(3):145-147．

［12］ Ribeiro V J，RiediR H，Baraniuk R G．Locating Available Band-width Bottlenecks［J］．IEEE Internet Computing，2004，8(5):34-41．

［13］ 戴佩华，薛小平，邵玉华．基于垂直平分线的区域定位算法［J］．计算机工程，2009，35(2):105-108．

［14］ 周四清，陈锐标．无线传感器网络APIT定位算法及其改进［J］．计算机工程，2009，35(7):87-89．

［15］ 汪 炀，黄刘生，肖明军，等．一种基于RSSI校验的无线传感器网络节点的定位算法［J］．小型微型计算机系统，2009，30(1):59-62．

［16］ 万国峰．基于锚节点和高斯函数的测距算法［J］．计算机工程，2013，39(2):73-76．