改进PID算法在气动位置伺服控制系统中的应用

林黄耀

(湄洲湾职业技术学院机械工程系，福建莆田351254)

气动位置伺服控制系统具有很强的非线性，这主要是由于气体的可压缩性、阀口复杂流动特性等因素的影响，因此气动位置系统的数学模型十分复杂，且模型中存在某些未知的参数，很难获得精确的数学模型，无法使用基于精确数学模型的一些控制方法(如自适应控制、极点配置方法等).本文采用传统的PID控制方法对气动位置控制进行了研究，通过调整比例、积分、微分三个参数对系统进行控制.这种控制算法由于简单实用，已被广泛用于工业领域，特别是过程控制领域.

1 常规位置式PID控制器

常规位置式PID控制器利用了实际值与目标值的偏差，将偏差的比例、积分、微分各环节通过线性组合构成控制量，对被控对象进行控制.其离散形式为

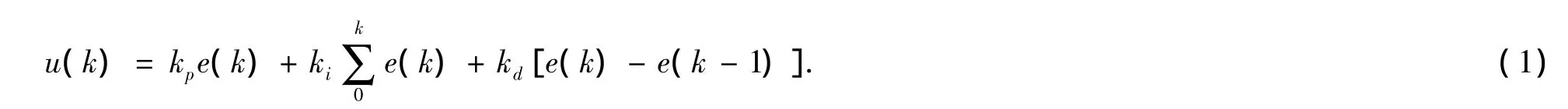
其中，u(k)是第 k次采样时刻计算机的输出，kp=KP，ki=KPT0/TI，kd=KPTD/T0，ki、kd分别称为积分系数和微分系数.

2 位置式PID控制仿真结果及分析

采用(1)的控制规则，在建立的系统数学非线性模型上进行仿真，仿真中选取不同的参数得到位移响应曲线如图1和图2所示.在图1中，kp为10，ki为30，kd为3;在图2中，kp为11，ki为6，kd为3.可以看出，图1中由于积分常数取得较大，系统出现了超调和积分饱和现象，不能稳定在目标位置附近;图2中由于积分系数取得较小，系统响应平稳，无超调，但其响应速度比较慢.由此可以看出，常规PID针对本系统还存在着不足，在应用于实验系统之前要先对其进行改进.

3 位置PID控制算法的改进

从上面的仿真结果分析中可知，由于在位置PID控制器中，积分系数ki在系统工作过程中是常数，在整个控制过程中，积分作用不变.当积分作用太强时，会使控制的动态性能变差以至于造成系统的不稳定.一般在误差比较大时，若引入积分作用，由于积分的记忆性，则在系统接近目标值时，容易使控制量保持很大值，使系统产生大的超调，不能快速精确地定位.因此，可以采用另外一种改进的PID控制算法，如(2)所示.

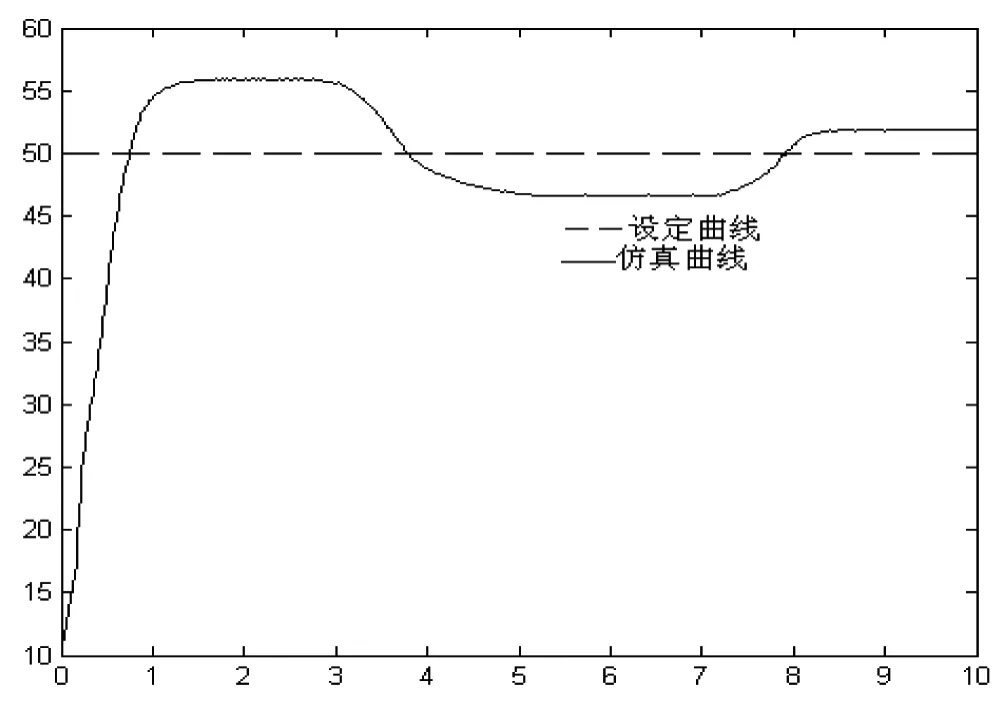
图1 积分系数较大时的位置PID控制阶跃响应仿真曲线

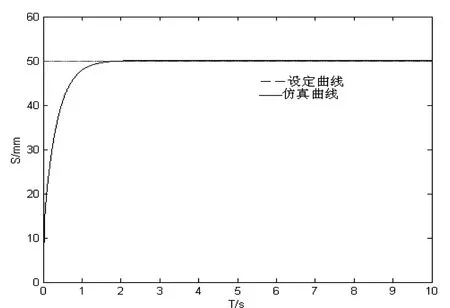
图2 位置PID阶跃响应仿真曲线

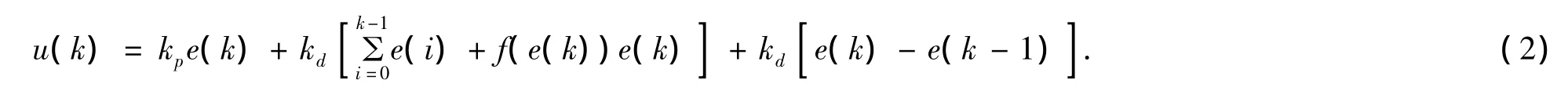
其中

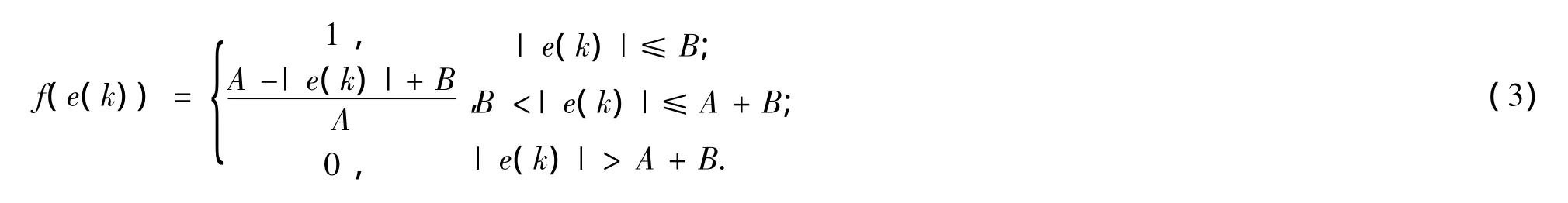
称(3)为变速积分PID算法，其中A、B为常数，其设计思想为设法改变积分项累加速度，使其与偏差大小相对应:偏差越大，积分越慢;反之则越快.可以看出，当|e(k)|增大时，f(e(k))减小，反之则增大.f(e(k))值在[0，1]区间变化，当某一时刻偏差|e(k)|大于A、B的和时，则积分环节不对该时刻的偏差进行累加，即f(e(k))=0;当某一时刻的偏差e(k)小于等于B时，加入当前值e(k)，积分环节与普通的PID积分项相同，积分速度最高;当偏差e(k)介于B和A+B之间时，则累加的该偏差的倍数用差值方法来计算.偏差越大积分越慢，偏差越小积分越快，且积分的速度是连续变化的.变速积分与积分分离控制方法很类似，但调节方式不同，前者对积分项采用的是缓慢变化，而后者则采用开关控制，而且变速积分对A、B两参数的要求不精确，因此使得变速积分调节质量更高.

这里我们采用变速积分控制对系统位置定位控制进行阶跃响应实验.在实验中，B和A+B的值均可从面板上进行赋值.将初始位置在10mm处，让其向右运动.实验中B取为0.5mm，A和B的和取为10mm，输入50mm的阶跃信号进行实验，得到的阶跃响应曲线如图3所示，实验中kp取值不同，ki为0.01，kd为12.

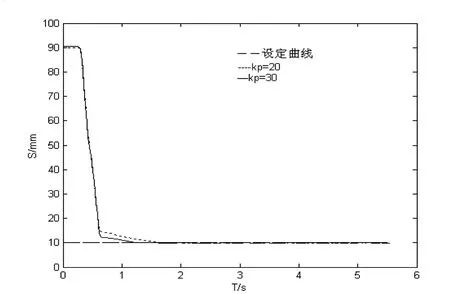
图3 变速积分阶跃响应实验结果

将(2)代入(4)得

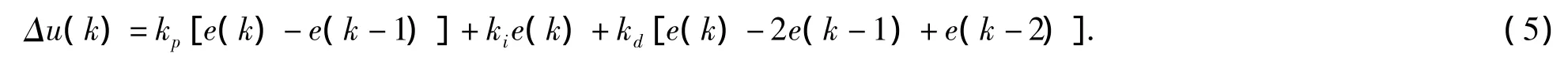
则(5)是通用的增量型PID算式.

在本系统中，采用增量式算法，计算机输出的控制增量Δu(k)对应的是比例流量阀开口的增量.虽然增量式算法与位置式算法并无本质区别，只是算法上作了一点改进，但相对于位置式控制算式却有以下优点:第一，因为输出是增量，即使偏差长期存在，输出Δu(k)一次次积累，最终可使执行器到达极限位置，但只要偏差Δe(k)换向，Δu(k)也立即变号，从而使输出脱离饱和状态，消除了发生积分饱和的危险;第二，输出只是增量，计算机误动作时造成的影响比较小，且控制平稳，必要时可用逻辑判断的方法去掉;第三，增大初始的控制量，提高系统的响应速度.

图4为增量PID控制器的实验曲线.可以看出，系统的响应速度得到提高，控制也比较平稳.

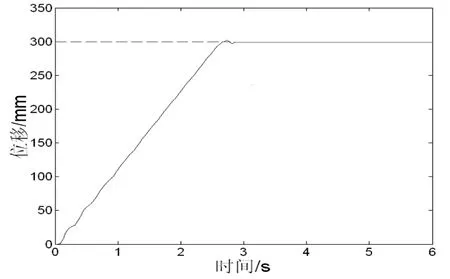
图4 增量式PID控制实验图

4 结语

综上所述，本文采用了常规的位置式PID控制方法对系统位置定位控制进行了仿真，仿真结果表明，位置式PID对积分参数的变化很敏感，系统会出现超调和积分饱和现象，不能稳定在目标位置附近，而当我们调整参数，满足系统稳定、无超调、高的定位精度要求时，系统的响应速度又会变慢.

并且，针对常规的位置式PID控制算法的不足，对其中的积分环节进行改进，提出了变速积分PID控制算法.采用变速积分PID控制算法对位置定位控制进行了实验研究.实验结果表明，该方法的系统响应速度比较快，具有一定的定位精度，稳态误差的绝对值在0.5mm内.由于位置式项不仅计算繁琐而且占用很大的内存，使用也不方便.所以我们又应用增量式PID对位置控制进行了实验研究.实验结果表明，该算法响应速度快，控制精度高，控制平稳.

[1]裘华徕.气动技术的近期发展及其影响因素[J].液压气动与密封，2002(3):1－3.

[2]李素玲，刘军营.比例控制与比例阀及应用[J].液压与气动，2003(2):30－32.

[3]王永昌，潘先耀.气动伺服控制系统及阀的应用形式[J].燕山大学学报，2002(3):206－208.

[4]庞国仲.自动控制原理[M].合肥:中国科学技术大学出版社，2010.