一维非线性扩散过程转移密度的高阶近似方法

谷 伟，赵梦飞，周 坤

（中南财经政法大学 统计与数学学院，湖北 武汉，430073）

一、引 言

近年来，随着利率市场化要求的不断提高，如何选择合适的利率模型来动态地描述利率的变化，成为一个亟待解决的问题。利率模型建立的核心问题就是如何利用已知的离散观测数据估计模型中的未知参数，而极大似然估计就是其中一种较常用的参数估计方法，在该方法中转移密度函数的获取是关键问题。一般来说，转移密度函数的近似方法有三种：一是数值求解扩散过程满足的Fokker－Planck偏微分方程，通过它获得相应的转移密度函数近似值［1－4］；二是 Hermite多项式近似法［5－6］；三是模拟极大似然估计法［7－9］。本文考虑转移密度的一种基于偏微分方程（PDE）的近似方法，该方法首先构造具有四阶精度的差分法替代二阶精度的Crank－Nicolson差分法数值求解与该利率模型相关联的偏微分方程，进而获得转移密度函数的近似解。数值模拟试验结果表明，所构造的具有四阶精度的差分法比Crank－Nicolson差分法和Euler法具有更高的效率，并考察所构造的四阶差分估计法在中国银行间同业拆借利率的实证分析，实证结果表明，在所考虑的样本区间内，中国利率的长期水平值是0．025 42，且中国货币市场利率粘性系数的值接近于1。

二、估计方法

考虑如下由一维随机微分方程所控制的扩散过程模型：

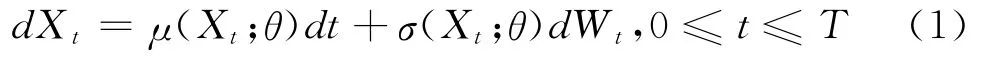
其中θ是未知参数向量，漂移项μ和扩散项σ是非线性函数，Wt是一维标准维纳过程。不妨令Δ＝titi－1为常数，假定扩散过程X在时间点0＝t0＜t1＜… ＜tN＝T上有离散观测值Xobs＝ （X0，X1，…，XN），且取值区间为［A，B］。

如果扩散过程X的转移密度p（Xt｜Xs；θ）（s＜t）已知，则可得如下似然函数：

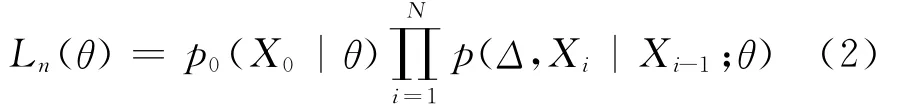
其中p（Δ，Xi｜Xi－1；θ）是两观测值Xi－1和Xi间的转移密度函数，则θ的估计值可通过最大化式（2），也可最小化为式（3）实现：

事实上，X的转移密度函数通常都是未知的，如何获得p（Δ，Xi｜Xi－1；θ），则成为一个关键问题。本文考虑了Euler估计法、基于偏微分方程的估计算法等方法近似p（Δ，Xi｜Xi－1；θ）。

（一）Euler法

Euler法是最简单的一种近似转移密度的方法，在时间区间［ti－1，ti］上，对式（1）采用 Euler算法进行离散：

其中序列 ｛εi－1｝相互独立且服从标准正态分布，则观测值Xi－1和Xi间的转移密度函数为：

其中mi－1＝Xi－1＋μ（Xi－1；θ）Δ，vi－1＝Δσ2（Xi－1；θ），pEuler表示在Euler法下转移密度函数的近似值。

（二）基于偏微分方程的估计方法

假定p（Δ，Xi｜Xi－1；θ）≡p（ti，Xi｜ti－1，Xi－1；θ），并记p（t，x）＝p（t，x｜ti－1，Xi－1；θ），Karatzas和Shreve指出转移密度函数p（t，x）是以下Fokker－Plank偏微分方程的解［10］282－290：

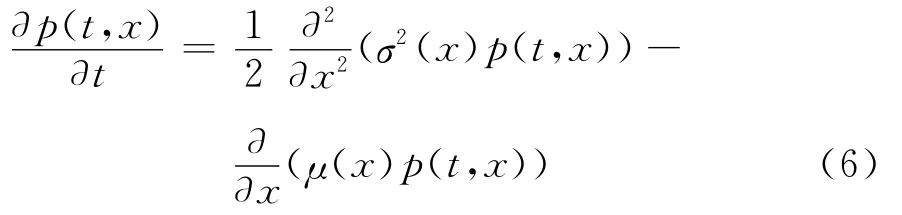
且满足初值条件：

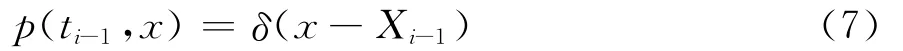
Poulsen指出，若扩散过程在边界处没有反射和吸收，可以假定式（6）满足如下边值条件［4］：

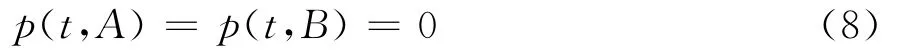
其中δ（·）为Dirac delta函数，如何处理Dirac delta初值函数成为一个棘手的问题。

式（6）可改写为：

其中a（x）＝0．5（σ2）xx－μx，b（x）＝ （σ2）x－μ，c（x）＝0．5σ2。

把区间［A，B］等分成n份，取步长为Δx＝ （B－A）／n，节点xk＝A＋kΔx （k＝0，1，…，n），同时把时间区间［ti－1，ti］以步长 Δt＝ （ti－ti－1）／m 等分成m 份，其中节点ti，j＝ti－1＋jΔt，（i＝1，2，…，N，j＝0，1，…，m），记r＝Δt／（Δx）2，pjk＝p（ti，j，xk）。

1．Poulsen采用的方法

采用Crank－Nicolson差分对式（9）进行离散，记ak＝a（xk），bk＝b（xk），ck＝c（xk），则可得如下格式：

实际算法实现中，还要对式（10）限定边值条件p0＝pN＝0，且选择均值为Xi－1＋μ（Xi－1；θ）Δt，方差 为 Δtσ2（Xi－1；θ）的 正 态 分 布 作 为 初 值 函 数 的近似［2］。

2．四阶差分法

现在考虑构造四阶差分方法求解式（6），首先，把式（9）改写成如下形式：

其中U（x）＝－b（x），D（x）＝c（x），S（x）＝a（x）。

在x∈ ［（k－1）Δx，（k＋1）Δx］，k＝1，2，…，n－1和t∈ ［ti＋jΔt，ti＋（j＋1）Δt］，i＝0，1，…，N－1，j＝0，1，…，m－1的小区间上，可以把式（11）

看成如下常系数偏微分方程

其中α＝U（xk），β＝ D（xk）。

令

由式（11）和（14）可得：

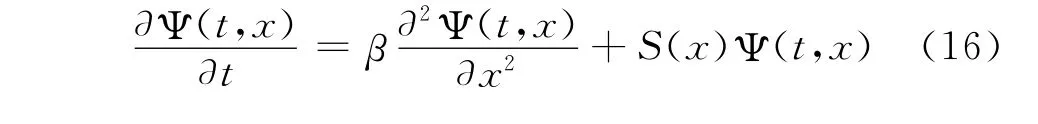
式（16）在［（k－1）Δx，（k＋1）Δx］，k＝1，2，…，N－1上成立，则有：

结合式（17）～（19），由三次样条差分公式可得式（16）的如下离散形式：

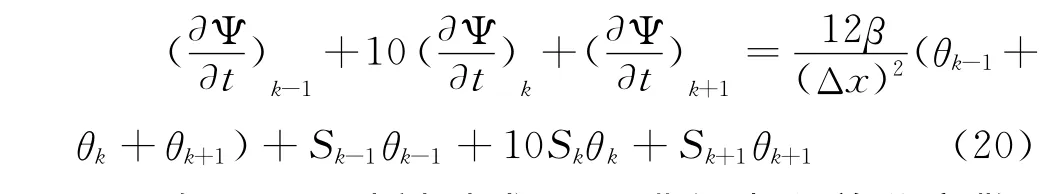
在ti，j＋1／2时刻 对式 （20）进 行中心 差 分 离 散，可得：

根 据 式（13）和（14），把 Ψ（t，x）＝ p（t，x）－1（x）φ－1（t）代入式（21），可得：

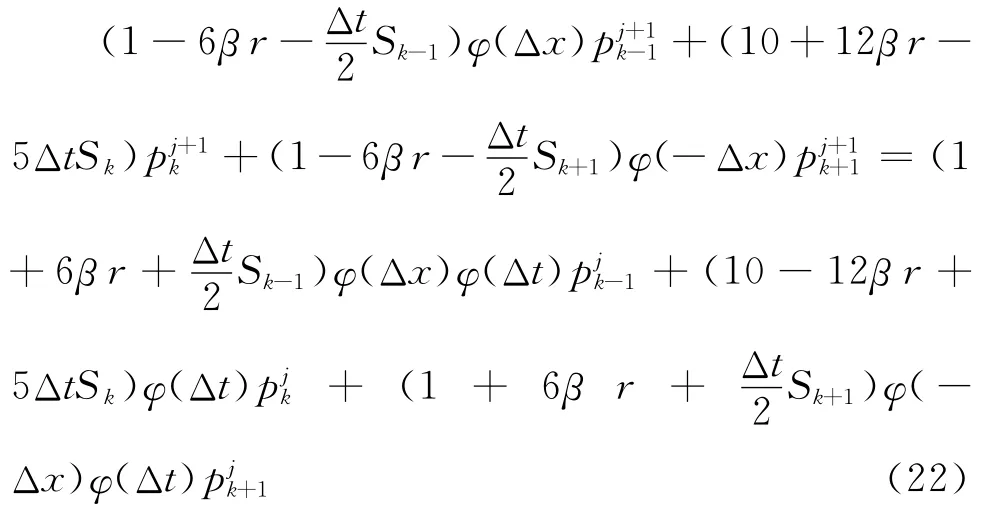
并可得出以下三条推论：(1)三个核心任务都无法完全自动完成，因此大脑在执行没意见任务时都需要使用精力资源；(2)三种核心任务之间相互竞争，至少是部分竞争的关系对精力资源的需求就会增加，大于只执行一项任务的认知负荷。(3)在大多数时候，口译员在工作时的认知水平处于接近于饱和的状态。导致议员大脑的处理能力跟不上，最终导致输出的译文质量下降。

式（22）是式（6）的离散格式，其精度为O（（Δt）2，（Δx）4），这意味着该离散格式具有时间2阶、空间4阶的精度，通过Fourier分析，可以证明差分格式式（22）是无条件稳定的。实际算法实现中，同样限定式（22）的边值条件为p0＝pN＝0，且选择均值为Xi－1＋μ（Xi－1；θ）Δt，方差为Δtσ2（Xi－1；θ）的正态分布作为初值函数的近似。

三、估计转移密度似然函数的效率

考虑存在转移密度函数的闭端解的CIR模型，便于进行Euler法和基于偏微分方程法估计效率的比较分析。

Cox、Ingersoll和 Ross提出了 CIR模型［11］。该模型满足如下随机微分方程：

其中θ1，θ2，θ3∈犚＋，且满足2θ1θ2＞θ23。CIR满足的转移密度函数为：cXi－1exp（－θ1Δ），v＝cx，Iq表示阶数为q的第一类修正Bessel函数。结合式（3）和（24），可得CIR模型参数的精确极大似然估计值。

为比较Euler法和基于偏微分方程估计法在近似密度函数的效率，我们先从给定数据获得近似对数似然函数和，也即，再利用式（24）获得精确对数似然函数和，最后再进行对比。为此，先对CIR模型做如下数值模拟实验以分别生成200个数据序列，其中每个数据序列包含501个数据点。每个数据序列可以这样产生，令式（23）中x0＝0．1，θ1＝0．2，θ2＝0．08，θ3＝0．1，t∈ ［0，500／12］，且取Δ ＝1／12，首先，在时间区间［0，500／12］上采用步长为1／12 000的 Milstein算法离散 式 （23）［12］345－351；然 后，在 时 间 点t0＝ 0，t1＝1／12，t2＝2／12，…，t500＝500／12上分别取值，可以得到一个数据序列，如此重复，最终生成200个这样的数据序列。

设Re（i）为由第i个数据序列获得的近似对数似然和和精确对数似然函数和的相对误差的绝对），值，记最大相对误差（MRE为 平均绝对相对误差（AARE）为Re（i）／R，平均平方相对误差（MSRE）为（Re（i）－AARE）2／R，其中R表示数据序列的总个数。利用三种方法分别计算200个数据序列的对数似然函数和的近似值，可得如下比较结果，见表1。此外，为比较估计方法对模型参数的估计偏差，我们定义了ARE：

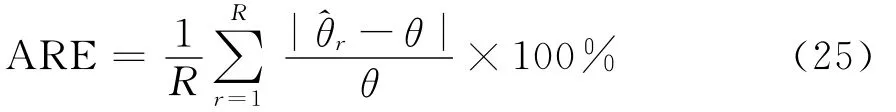
表1结果说明，对于CIR模型，四阶差分法近似的对数似然和的效果是最好的，其次是Poulsen法，且空间步长越小，近似效果越好。另外，从表2可以看出，四阶差分法对CIR模型参数的估计值最接近EML法，且估计偏差均小于Poulsen法。

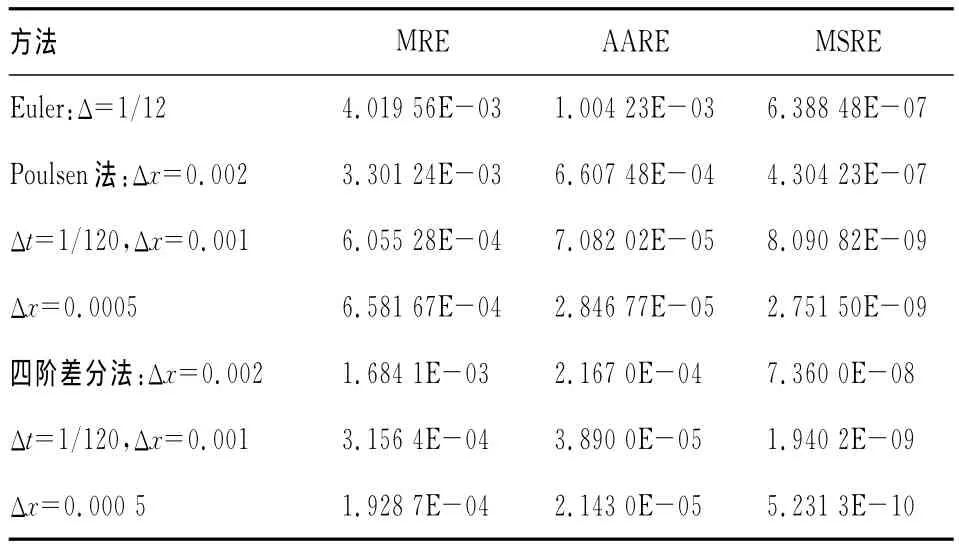
表1 Euler法和基于偏微分方程法估计CIR模型转移密度对数似然函数和的误差比较

表2 Euler法和基于偏微分方程法估计CIR模型参数的平均值和ARE（单位：%）

总的说来，四阶差分法对于对数似然和的近似效果均优于Poulsen法和Euler法，且对于模型参数的估计效果要优于Euler法和Poulsen法。实际应用中，在计算需求允许的条件下，对于基于偏微分方程的估计法，尽量取较小的空间步长，以获得更为精确的估计结果。

四、实证分析

这里考虑CKLS模型对实际数据进行描述，它是一个最基本的利率过程模型，国内外很多实证研究都是基于该模型进行的［13］。其具体形式为：

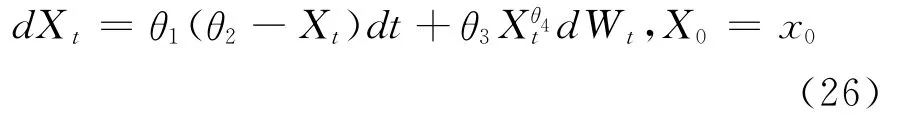
其中利率的均值回复速度θ1、利率的均值回复水平θ2、利率的波动系数θ3、粘性系数θ4为四个待估参数，该模型的转移密度函数无法解析表达。

本文收集了1996年2月至2010年3月中国银行间货币市场的拆借利率IBO007，所使用的是每月加权后的平均利率，共计170个月度数据（数据来源：中国货币网，www．chinamoney．com．cn）。由于拆借利率按单利计算，不妨按下述公式将其转换为等价连续复利：R（t）＝52ln（1＋r（t）／52），其中r（t）表示观测的加权平均利率，R（t）表示转换后的连续复利。可以获得变换后170个数据的描述性统计特征，均值为0．038 1，标准差为 0．029 2，偏度为3．866 2，峰度为1．527 3，最大值为0．112 4，最小值为0．010 2，其时间序列图如图1。

图1 连续复利R（t）的时间序列图

从时间序列图上看，从1996年2月到1999年12月，2006年5月到2009年1月这两个期间内数据波动比较厉害，前段时期是中国货币政策发生重大调整的时期，后段时期是受次贷危机的影响而频繁调整货币政策。表3列出了利用R（t）获得CKLS模型的参数估计结果。从估计结果上来看，Euler法和四阶差分法的估计结果有较大差异，Euler法的估计效果较差。在所考虑的样本区间内，由Euler法和四阶差分法所获得利率的均值回复水平θ2分别为0．024 76和0．025 42，均低于样本的平均利率0．038 1，这是由于波动系数θ3是均值回复水平的3～13倍，同时，可以看出四阶差分法计算的均值回复水平更接近样本平均利率。另外，所估计的粘性系数θ4的值接近于1，说明CKLS模型比通常所用的CIR模型（θ4＝0．5）更适合对实际数据进行建模。

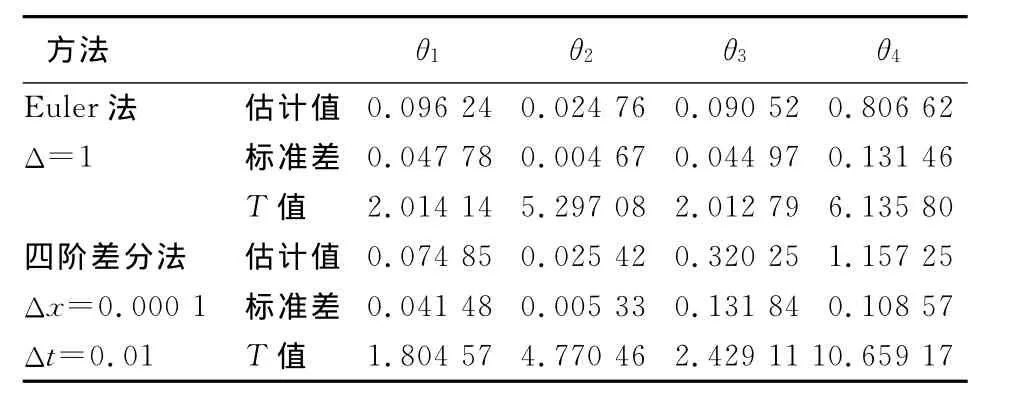
表3 CKLS模型的参数估计结果

五、结 论

本文构造了基于四阶差分的估计算法对利率扩散模型进行参数估计，并和Euler法和Poulsen法进行了对比。从第三部分的数值实验结果来看，四阶差分法对于对数似然和的近似效果均优于Poulsen法和Euler法，且对于模型参数的估计效果要优于Euler法和Poulsen法。此外，考虑了这两种估计算法在中国银行间货币市场拆借利率中的应用，在所考虑的样本区间内，中国利率的长期水平值是0．025 42，且中国货币市场利率的粘性系数θ4的值接近于1。

［1］ Lo A W．Maximum Likelihood Estimation of Generalized Lto Processes With Discretely Sampled data［J］．Econometric Theory，1988，4（2）．

［2］ Jensen B，Poulsen R．Transiton Densities of Diffusion Processes：Numerical Comparison of Approximation Techniques［J］．The Journal of Derivatives，2002，9（4）．

［3］ Hurn A S，Jeisman J，Lindsay K A．Transitional Densities of Diffusion Processes：A New Approach to Solving the Fokker－planck Equation［J］．The Journal of Derivatives，2007，14（4）．

［4］ Poulsen R．Approximate Maximum Likelihood Estimation of Discretely Observed Diffusion Processes［R］．Working paper 29，Center for Analytical Finance，University of Aarhus，1999．

［5］ Ait－Sahalia Y．Maximum Likelihood Estimation of Discretely Sampled Diffusions：A Closed form Approximation Approach［J］．Econometrica，2002，70（1）．

［6］ Ait－Sahalia Y．Closed－form Likelihood Expansions for Multivariate Diffusions［J］．The Annals of Statistcs，2008，36（2）．

［7］ Pedersen A R．A New Approach to Maximum Likelihood Estimation for Stochastic Differential Equations Based on Discrete Observations［J］．Scandinavian Journal of Statistics，1995，22（1）．

［8］ Brandt M，Santa－Clara P．Simulated Likelihood Estimation of Diffusions with an Application to Exchange Rate Dynamics in Incomplete Markets［J］．Jurnal of Financial Economics，2002，63（2）．

［9］ Durham G B，Gallant A R．Numerical Techniques for Maximum Llikelihood Estimation of Continuous－time Diffusion Processes［J］．Jurnal of Business ＆ Economics，2002，20（3）．

［10］Karatzas I，Shreve S．Brownian Motion and Stochastic Xalculus［M］．2nd ed．New York：Springer－Verlag，1992．

［11］Cox J C，Ingersoll J E，Ross S A．A Theory of the Term Structure of Interest Rates［J］．Econometrica，1985，53（2）．

［12］Kloeden P，Platen E．Numerical Solution of Stochastic Differential Equations［M］．Berlin：Spinger－Verlag，1992．

［13］Chan K C，Karolyi G A，Longstaff F A，et al．An Empirical Comparison of Alternative Models of the Short－term Interest Rate［J］．Journal of Finance，1992，47（3）．