中国宏观经济不确定性的统计测度研究

章上峰，李荣丽，王玉颖

（浙江工商大学 统计学院，浙江 杭州310018）

一、引 言

宏观经济不确定性是政府制定宏观经济政策需要考虑的重要因素之一。经济理论构建面临一个不可回避问题：只有排除不确定性才能进行经济分析，但是对于经济政策而言，只有考虑到不确定性才更有实际意义。奈特将“不确定性”和“风险”做了区分。凯恩斯认为不确定性是宏观经济的核心，将不确定性和宏观经济学紧密联系起来。不确定性对于宏观经济政策制定的重要性毋庸置疑，量化测度是关键的一步。早期关于宏观经济不确定性的研究，利用宏观经济波动作为不确定性的代理变量，常用的度量方法有标准差法、极差法、移动平均标准差等，这些方法均假定经济变量值的波动为常数波动，用经济变量的历史波动作为未来经济变量波动的无偏估计［1－3］。奈特定义概率型随机事件的不确定性为风险，定义非概率型随机事件为不确定性。这一定义得到了经济学者的广泛认同，如王健宇将居民收入不确定性定义为居民收入具有的无法准确观测、分析和预见的变化［4］。本文定义宏观经济不确定性是指人们无法准确观测、分析和预见的经济变化，即经济体预期值与实际值的偏离。尽管标准差这一指标可反映不同时间、不同群体间的差异程度，但这种差异程度又是导致人们预期不确定性的重要因素，所以这一指标并不能代表真实的不确定性。现实中宏观经济波动是时变的，因此标准差也应该是时变的。

当前，国际学术界的通行做法是采用隐含波动率（Volatility Index，VIX）指标作为宏观经济不确定性的代理变量［5－7］。VIX是由CBOT所编制，是芝加哥期权期货交易所使用的市场波动性指数，由S＆P500的成分股的期权波动性组成，可用来预期未来30天市场波动性。VIX广泛用于反映投资者对后市的恐慌程度，又称“恐慌指数”，指数愈高，意味着投资者对股市状况越感到不安。VIX有效剔除了经济体可预期部分，是对宏观经济不确定性的合意代理变量。研究表明，隐含波动率与一系列不确定性代理变量显著相关，这些代理变量包括实际收入增长率以及金融分析师对经济预测的偏离［5］。Bloom用VIX测度不确定性，验证了股票市场的VIX与其他代表性的宏观、微观不确定性变量高度相关［6］。

中国期货期权市场不完善，没有隐含波动率指标，因而不能用来测度中国的宏观经济不确定性。本文提出利用剔除预期的计量经济模型，来测度宏观经济不确定性，并比较不同测度模型的优缺点，为正确认识宏观经济不确定性和制定经济政策提供量化测度结果。

二、统计测度模型

宏观经济不确定性为经济体预期值与实际值的偏离，并非所有的宏观经济波动都属于宏观经济不确定性范畴。选择剔除可预期部分的计量经济模型作为宏观经济不确定性的测度方法［8］。常用计量经济模型包括GARCH模型、随机波动模型和马尔科夫机制转移模型等。

（一）GARCH 模型

标准的GARCH（1，1）模型为：

其中，xt＝ （x1t，x2t，…，xkt）′ 是解释变量向量，γ ＝（γ1，γ2，…，γk）′是系数向量。由于σ2t是以前面信息为基础的一期向前预测方差，式（2）称为条件方差方程。利用GARCH模型测度的不确定性σ2t，是基于前期波动性的信息u2t－1和上一期的预测方差σ2t－1，即GARCH模型测度的不确定性剔除了经济体的预测，更真实反应了经济体面临的宏观经济不确定性。

在测定不确定性方面，GARCH模型既解决了波动的时变性，又解决了非预期的经济变量波动性问题。由GARCH模型估计得到的标准差可以反映宏观经济变量的非预期波动。GARCH模型拟合的条件方差序列作为宏观经济不确定性的代理指标，可以剔除自变量变化趋势，反映宏观经济变量的非预期波动。GARCH族模型能在给定经济结构下，明确估计出的条件方差是事前的方差而不是像标准差的事后方差，它可以更好地反映不确定性。因此，GARCH模型比标准差更精确，成为宏观经济不确定性测度的主要方法之一［9－10］。

（二）随机波动模型

GARCH模型也存在新的问题，当存在异常观测经济变量值时，将使估计的条件方差突然变动，即估计的波动性序列不是很稳定。此外，GARCH族模型对于长期波动性的预测能力较差。为克服这一缺陷，Harvey和Jacpuier于1994年将随机波动模型（SV模型）引入计量经济学。在随机波动模型中，条件方差不再是一个确定性函数，而是加入了随机项的条件方差，从而可以反映随机因素对波动性的影响。与GARCH模型不同，随机波动模型的波动性不仅依赖于以前的波动，还依赖于当前的信息。

令宏观经济变量序列为｛xt｝，均值修正的序列

其中，t＝1，2，…，n，｛ut｝和｛νt｝是互不相关的白噪声序列，θt决定了变量t时刻的波动，φ（－1＜φ＜1）表示y对数平方项的自相关性，φ为持续性参数，度量了波动的持续性，反应当前波动对未来波动的影响，常数项β＝exp（μ／2）表示初始波动均值，τ表示y对数波动的波动。

目前估计SV模型的方法主要有：广义矩估计法、模拟极大似然法、蒙特卡罗极大似然法以及马尔科夫链蒙特卡罗估计法（MCMC法）等。其中，基于贝叶斯原理的估计参数后验分析的MCMC法使用最广。该方法利用了模型信息和样本数据信息，将马尔科夫过程引入到Monte Carlo模拟中以实现动态模拟，其基本思路是通过构造一个平稳分布为特定密度分布函数的马尔科夫链抽样，基于这些抽样做出各种统计推断。

（三）马尔科夫模型

GARCH模型和随机波动模型都是利用样本数据对模型参数进行估计，以估计模型为基础，计算相应时期的方差来估计宏观经济不确定性。但是，这两个模型都隐含了一个假设，即不同时期的经济结构相同，模型参数不变。尽管时变GARCH模型以及时变SV模型考虑到了结构变化，但却没考虑到未来可能区域转变对不确定性产生的影响［11］。马尔科夫范式转换模型（MRSM）针 对未来区域转变不确定对经济变量的总不确定程度做出估计。假设某宏观经济变量x在两状态之间转变（状态0和状态1），令为在给定t期信息的情况下，t＋1期为状态1的概率，则给定t期信息的情况下，t＋1期为状态0的概率为。事后预测偏差可表示为：

定义宏观经济变量x的不确定性为条件方差Var（xt＋1｜Ωt），该条件方差将受到状态概率的影响，其影响如下所示：

该等式右边第一项表示方差不确定性，即不同状态宏观经济变量x方差的期望值；第二项表示均值不确定性，即宏观经济变量期望值的条件方差。其中：

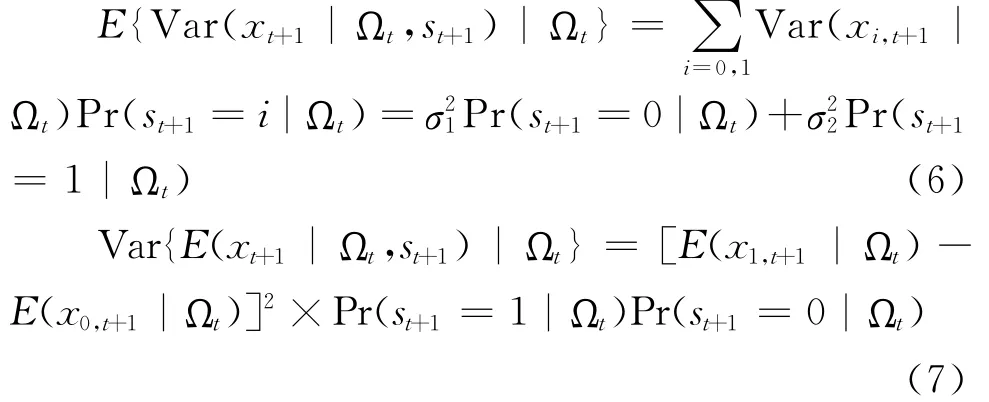
三、实证结果

宏观经济景气指数是综合反映各行业运行状况的定量指标，包括预警指数、一致指数、先行指数、滞后指数，本文采用包括预警指数和一致指数作为替代变量，测度中国宏观经济不确定性，数据区间为1992年1月－2014年5月，数据来源于国家统计局网站。GARCH模型、随机波动模型和马尔柯夫模型均采取AR自回归方式来剔除经济预期，并利用估计得到的条件方差来测度宏观经济不确定性。

（一）GARCH 模型

对预警指数进行ADF单位根检验，在0．1的显著水平下，预警指数为平稳序列。对预警指数做ARCH效应分析与GARCH（1，1）分析，发现条件异方差检验的F－statistic值对应的P值变大。对一致指数进行ADF单位根检验，结果表明，在0．05的显著水平上，一致指数为平稳序列。基于GARCH（1，1）得到预警指数、一致指数的条件异方差如图1所示。

图1 宏观经济不确定性GARCH模型测度结果图

由图1可知，预警指数不确定性较大的时间点为：1993年2月、1993年11月、1994年9月、1995年9月、1999年11月至2000年2月、2003年10月、2004年6月、2008年10月至2009年1月、2010年10月；其中1993年至1995年和2008年10月至2009年1月，预警指数不确定性整体很大。对应的时间点为，一致指数不确定性波动也很大，相对而言预警指数不确定性变动更频繁，并且预警指数不确定性提前达到波峰。个别时点上，如2003年10月份，预警指数不确定性很大，一致指数不确定性也出现了小幅波动，但波幅不剧烈。以上结果说明预警指数和一致指数不确定性的GARCH模型测度结果基本一致，相对而言，预警指数更加敏感和领先，一致指数更加稳健。

（二）随机波动模型

建立SV模型，利用Winbugs14估计模型参数。使用MCMC对参数估计之前，对参数分布及需要迭代的初始值进行设置。根据Kim参数设置，令α＝0，β＝0．975，τ2＝50。迭代次数越多，参数的初始值设置对迭代结果影响越小。考虑到前面迭代的非平稳性，通过“燃烧”先舍去前40 000个抽样值，取后40 000个抽样值，模型共运行80 000次。估计得到预警指数和一致指数SV模型的参数估计值，参数估计值趋于平稳，表示模型收敛。计算得到隐含波动序列θt，根据θt＝lnσ2t，可知方差序列σ2t（如图2所示）。

由图2SV模型测度结果可知，预警指数不确定性在七个时间点较高，分别是1992年9月、1995年9月、1998年9月、2000年2月、2003年9月、2009年4月和2013年5月。一致指数不确定性在六个时间点较高，分别是1993年3月、1995年12月、1998年3月、1999年8月、2002年10月、2008年12月。一致指数与预警指数不确定性基本一致，相对稳健和延后。一致指数SV模型对于2008年的美国次贷危机刻画较为敏感和突出。

图2 宏观经济不确定性SV模型测度结果图

（三）马尔科夫机制转换模型

马尔科夫自回归模型中，对于每个状态下的自回归，均要求平稳序列，因此，马尔科夫自回归模型使用的序列是经检验或处理后的平稳序列。预警指数和一致指数的马尔科夫两状态方程如下（一致指数方程由括号中的系数表示）：

状态1：ZHSH ＝1．91（4．05）＋0．95（0．96）·ZHSH（－1）

状态2：ZHSH ＝ 2．33（－5．65）＋ 0．99（1．06）·ZHSH（－1）

估计得到预警指数转移概率如下：若t时期为第一状态，t＋1期仍为第一状态的概率为0．72，t＋1期为第二状态的转移概率为0．28；若t时期为第二状态，t＋1期为第一状态的概率为0．13，t＋1期仍为第二状态的转移概率为0．87。对应地，估计得到一致指数转移概率如下：若t时期为第一状态，t＋1期仍为第一状态的概率为0．96，t＋1期为第二状态的转移概率为0．04；若t时期为第二状态，t＋1期为第一状态的概率为0．19，t＋1期仍为第二状态的转移概率为0．81。

总不确定性分解结果如图3所示，结果说明总不确定性与方差不确定性在数值上较为接近，但是总不确定性变化主要是由均值不确定性的变化引起的。根据马尔科夫取值转移模型测度结果，预警指数不确定性较大的七个时间点分别为：1993年8月、1995年2月、1999年11月、2004年4月、2008年4月、2009年7月和2010年4月；一致指数不确定性较大的六个时点分别为：1993年3月、1999年4月、2004年4月、2008年5月、2009年4月和2010年4月。两者结果基本一致，一致指数不确定性相对稳健和延后。

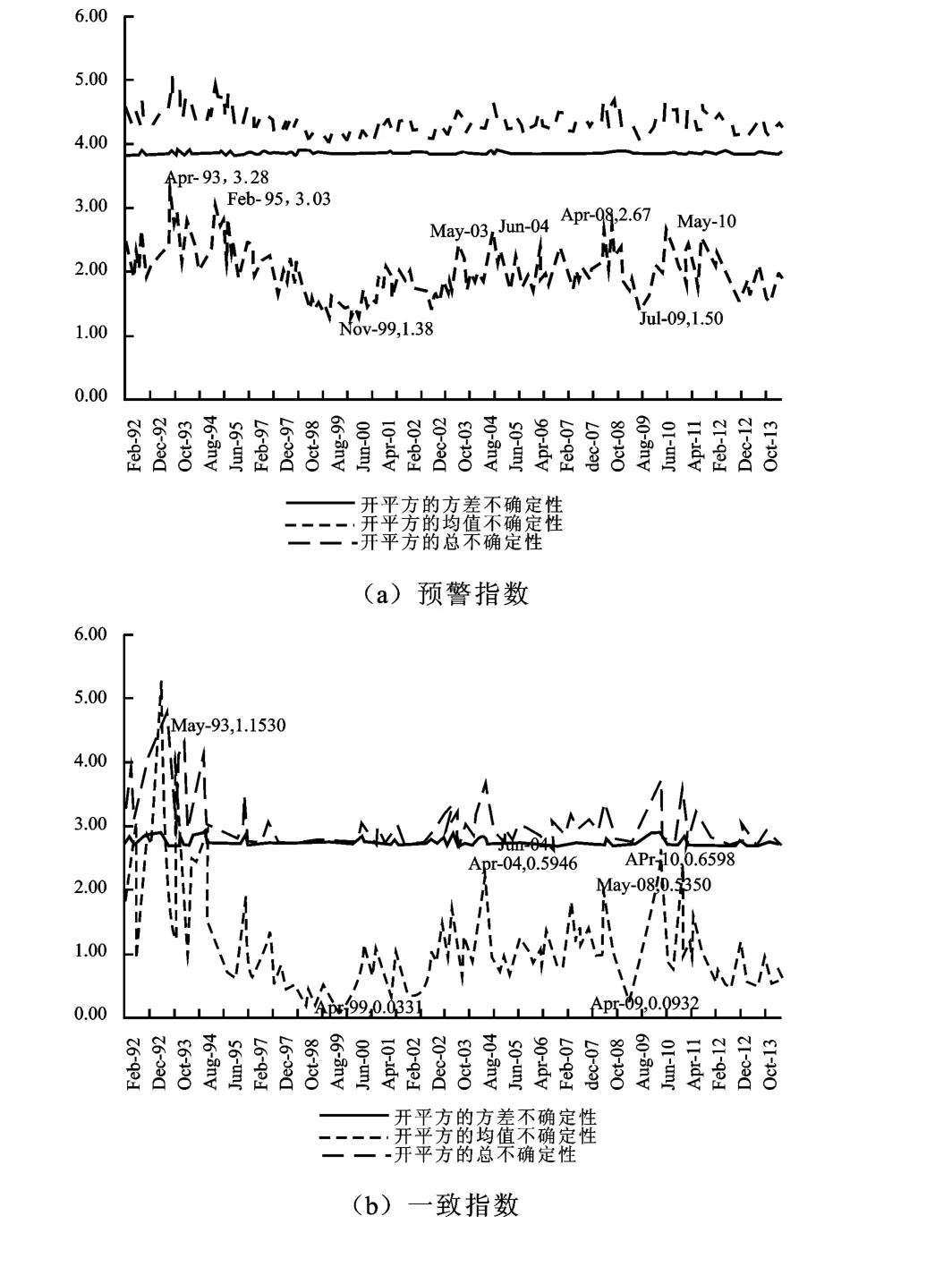
图3 预警指数和一致指数总不确定性及其均值、方差分解图

（四）经济解释

由以上统计测度结果可知，中国宏观经济不确定性较大的时期主要分布在1993－1995年，1997－2000年、2008－2009年和2010－2011年。可能的经济解释如下：

1988年高通货膨胀，中国政府采取了紧缩型政策，进行为期三年的大整顿，对经济实体造成了不利影响。1992年邓小平南巡讲话以来，中国经济高投资、高增长、价格大幅上涨，1993年下半年开始，政府采取一系列措施调控经济。因此，1993－1995年预警指数和一致指数不确定性均很大，反映了中国市场经济体制确立后的宏观经济不确定性增加的事实。

1997年亚洲金融危机爆发，打破了世界经济增长的“亚洲奇迹”，中国政府承诺并奉行“人民币不贬值”货币政策，获得了国际社会好评。但是，在1999年世界经济增长率高于上年的情况下，中国承受了1999年经济增长率低于上年、2000年仍未完全恢复等困难。2008年美国金融危机波及全球，世界经济增长率下降超过1个百分点，中国政府推出“4万亿”经济刺激计划，货币政策由“稳健”、“从紧”改为“适度宽松”，再次获得了国际社会好评。但是，中国政府2009－2010年面临通货膨胀、产能过剩、银行信贷剧增以及产业结构没有优化等困难。应对最近的欧洲主权债务危机，中国政府统筹稳增长、调结构、促改革，在财政政策方面“调整支出结构，压缩行政开支，加快支出进度，对小微企业实行税收优惠”；在货币政策方面“保持定力，既不放松也不收紧银根，管理好流动性，重点通过盘活存量、用好增量，支持实体经济发展”。2010－2013年中国经济增长率缓慢下降，目前保持在7%～8%之间，没有出现通货膨胀，也未出现经济“硬着陆”。1997－2000年、2008－2009年和2010－2011年预警指数和一致指数不确定性较大，反映了中国经济面临亚洲金融危机、美国次债危机和欧洲主权债务危机背景下，宏观经济不确定性增加的情况。

面对经济领域的重大突发事件，预警指数不确定性都会大幅波动，而一致指数不确定性只有对中国整体宏观经济产生重大影响才会引起出现大幅波动。这也说明预警指数不确定性反映灵敏，适合于短期分析和局部一般事件应用，一致指数不确定性反映平缓，适合于长期分析和重大事件应用。

目前，国际上通常使用美国市场波动率指数VIX来代表全球宏观经济不确定性（见图4）。由图4可知，全球宏观经济不确定性较大的几个时间点为：1997年11月12日、1998年10月8日、2001年9月20日、2002年8月5日、2008年11月20日、2010年5月20日、2011年8月8日。1997－1998年对应亚洲金融危机、2001－2002年对应美国“9．11”事件、2008年对应美国金融危机，2010－2011年对应财政悬崖和欧洲主权债务危机。VIX指数全面反映了全世界范围的突发事件冲击导致的宏观经济不确定性。

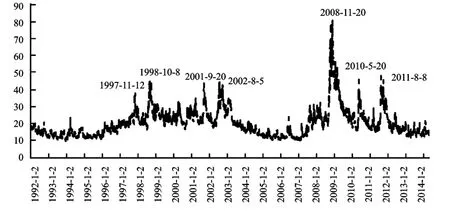
图4 美国市场波动率指数VIX图

GARCH模型、随机波动模型和马尔柯夫机制转移模型，采取自回归方式来剔除经济预期，并利用条件方差来测度时变不确定性。但是，三个模型设定形式不同，模型机理不同，所得的研究结论也会有所差异：GARCH模型的水平冲击和方差冲击是一致的，而随机波动模型和马尔柯夫机制转移模型可以分离水平冲击和方差冲击［13］；GARCH模型和随机波动模型测度条件方差利用的是连续函数形式，而马尔柯夫机制转移模型利用的则是离散函数形式。因此，需要根据研究对象和性质的不同，选择合适的计量经济模型。本文将GARCH模型、随机波动模型和马尔科夫机制转移模型的测度结果与VIX指数进行对比发现，利用随机波动模型测度得到的宏观经济不确定性与VIX指数在趋势上最为一致。这说明利用随机波动模型测度宏观经济不确定性是合意的。

四、研究结论

本文选择宏观经济景气指数作为代理变量，分别利用GARCH模型、随机波动模型和马尔科夫机制转移模型等计量经济模型，来测度中国宏观经济不确定性。实证研究发现，中国宏观经济不确定性较大的时期主要分布在1993－1995年、1997－2000年、2008－2009年和2010－2011年，分别对应中国市场经济初期、亚洲金融危机、美国金融危机和欧洲主权债务危机时期。三种模型对于宏观经济不确定性较大的时间点测度结果基本一致，但在具体数值和结果形式上，不同模型有着很大差异，这可能是由于以下几个方面的原因造成：第一是数据处理过程不同，GARCH模型、马尔科夫模型要求平稳化数据，本文使用HP滤波后的平稳数据，而随机波动模型使用的是对数差分去均值后的数据。第二是模型机理不同，GARCH模型包含均值方程和条件方差方程；随机波动模型中，条件方差不再是一个确定性函数，而是加入了随机项的条件方差，从而反映出随机因素对波动性的影响；马尔科夫机制转移模型可以估计未来区域转变不确定对经济变量总不确定程度。相对而言，随机波动模型，宏观经济不确定性的测度结果更为平滑，结论与VIX指数最为一致。

经济领域的重大突发事件，预警指数不确定性都会大幅波动，而一致指数不确定性只有对中国整体宏观经济产生重大影响才会引起大幅波动。这也说明预警指数不确定性反映灵敏，适合于短期分析；一致指数不确定性反映平缓，适合于长期分析。

本文比较了不同测度模型的优缺点，为正确认识宏观经济不确定性和制定宏观经济政策提供量化测度结果。由于中国国民经济核算年鉴可查询的时间周期过短，选择工业生产者出厂价格指数（PPI），以及制造业采购经理人指数（PMI）、银行间同业拆借利率、M2等重要的宏观经济指标，对宏观经济不确定性进行更加全面地测度，是下一步值得研究的方向。

［1］ 宋铮．中国居民储蓄行为研究［J］．金融研究，1999（3）．

［2］ 申朴，刘康兵．中国城镇居民消费行为过度敏感性的经验分析：兼论不确定性、流动性约束与利率［J］．世界经济，2003（1）．

［3］ 罗楚亮．经济转轨、不确定性与城镇居民消费行为［J］．经济研究，2004（4）．

［4］ 王健宇．收入不确定性的测算方法研究［J］．统计研究，2010（9）．

［5］ N Bloom，S Bond，J Van Reenen．Uncertainty and Investment Dynamics［J］．Review of Economic Studies，2007（2）．

［6］ N Bloom．The Impact of Uncertainty Shocks［J］．Econometrica，2009（3）．

［7］ S Basu，B Bundick．Uncertainty Shocks in a Model of Effective Demand［R］．National Bureau of Economic Research，2012．

［8］ A Orlik，L Veldkamp．Understanding Uncertainty Shocks and the Role of Black Swans．Unpublished Manuscript［C］．New York University Stern School of Business，2012（12）．

［9］ 王义中，宋敏宏．宏观经济不确定性、资金需求与公司投资［J］．经济研究，2014（2）．

［10］胡永宏，焦莉莉．国际油价不确定性与中国经济增长——基于GARCH－in－Mean SVAR模型的实证研究［J］．统计与信息论坛，2013（10）．

［11］Martin Evans，Paul Wachtel．Inflation Regimes and the Sources of Inflation Uncertainty［J］．Journal of Money，Credit and Banking，1993（3）．

［12］赵留彦，王一鸣，蔡婧．中国通胀水平与通胀不确定性：马尔科夫域变分析［J］．经济研究，2005（8）．

［13］Jesús Fernández－Villaverde．Macroeconomics and Volatility：Data，Models，And Estimation［R］．NBER Working Paper Series16618，2010．