中国经济增长方式转变特征测度——基于贝叶斯时变参数状态空间模型<br/>

中国经济增长方式转变特征测度——基于贝叶斯时变参数状态空间模型

2015-01-01张五六

统计与信息论坛 2015年6期

张五六

（华侨大学数量经济研究院，福建厦门361021）

一、引言

如何合理而准确地测度经济增长方式转变是当前中国经济研究的一个热点问题，也是中国经济转型特征研究的重要基础。研究的核心在于中国经济增长进程中，投入的生产要素及全要素生产率（TFP）是如何促进经济增长方式转变的，转变的历史路径又具有什么样的时代特征。研究的主要内容有三个方面：一是生产要素对经济增长的弹性如何，是否满足规模报酬不变的假定？二是全要素生产率对经济增长如何，进入本世纪后全要素生产率是乐观还是堪忧的，对未来经济的增长是否具有一定的持续性支撑？三是生产要素与全要素生产率是否存在一定的关联，是否通过人力资本的外部性促进了TFP值的变化？

在相关经典文献研究中，对于中国经济增长方式转变测度研究在最近十几年来得到蓬勃发展，但从发展的脉络来看，与本文研究密切相关的内容有三个方面，即经济增长方式转变的理论模型设置、计量模型及估计、相关数据核算问题。现存相关文献为本文研究提供了前期基础，也为进一步创新性研究中国经济增长方式转变测度带来新的启发。

在理论模型设置方面，主要有两个方面的理论模型：一是基于Solow增长模型的测算方法［1］。该理论模型只考虑到劳动及物质资本要素，是在CD生产函数基础上发展而来的。该方法在中国经济增长方式转变测度中应用非常广泛，如郭庆旺和贾俊雪采用该模型对中国1978－2004年的数据进行了分析，发现1993年以前全要素生产率（TFP）剧烈频繁变化，1993年后TFP增长率总体呈现出逐年下降的趋势，直到2000年下降趋势才得以缓解［2］。二是基于Lucas增长模型的测算方法［3］。该理论考虑到劳动、人力资本及物质资本要素，是在C－D生产函数基础上拓展而来的。该模型存在两种设置方式。第一种方式是将平均人力资本水平对劳动力相乘获得“有效劳动力”要素，并且将其用来替代劳动力要素；第二种方式是在第一种方式的基础上再乘以平均人力资本水平，并将其用来考察人力资本的外部性。如：Wang和Yao采用第一种设置方式，在核算1952－1999年间中国人力资本存量数据的基础上，分析发现改革以前TFP值为负值，改革后TFP值为正值［4］；景跃军和刘晓红采用第二种设置方式，在核算1990－2010年间中国人力资本存量数据的基础上，分析发现中国经济的发展主要是以物质资本促成经济规模扩张的，而人力资本则累积不足［5］。

在计量模型及估计方面，主要存在固定参数及时变参数方法，如郭庆旺和贾俊雪对基于Solow增长模型的测算方法应用，Wang、Yao、景跃军和刘晓红、汤向俊对基于Lucas增长模型的测算方法应用均采用了基本的线性回归方法，都属于传统固定参数的计量分析方法［4－6］；而高宇明和齐中英、陈娟均构建了具有时变参数特征、规模报酬不变的C－D生产函数，分别研究了1952－2005年、1978－2005年间中国TFP特征，发现其均具有时变的现象［7－8］；章上峰和许冰同样构建了具有时变参数特征、规模报酬不变的拓展型C－D生产函数，估计了资本、劳动力和全要素生产率的逐期贡献率［9］。

相关数据的核算问题方面，主要存在于劳动力、物质资本及人力资本存量方面。一是劳动力主要采用各年统计年鉴年底的全社会就业数据，但由于在第五次人口普查之后，国家统计局对1990－2000年的就业人员数据进行了调整，使得1990年前后人口数据统计口径变得不一致，这时就需要对原始数据进行调整，如王小鲁、樊纲对此进行了具体讨论，并给出了调整方法［10］54－64；二是物质资本存量方面，早期Chow对中国的物质资本存量展开了核算，后来王小鲁、樊纲等对此核算有所发展，随着核算方法的完善以及统计资料的完备，相关学者核算的物质资本存量数据均逐渐趋同［11－12］；三是人力资本存量方面，通常采用受教育年限法，如 Wang、Yao、景跃军和刘晓红、汤向俊、王小鲁和樊纲等均采用该方法核算出了不同阶段的人力资本存量。

从中国经济增长方式转变测度的三个焦点方面的文献研究来看，一是选择什么样的理论模型才是最合适的。这在文献研究中多有争论，然而没有一篇文献对此作出选择性的回答。本文拟在此方面作出探索性的研究，即首先序贯性的建立基于Solow、Lucas增长模型的所有理论模型，然后根据模型估计结果对其进行模型比较与选择，得到一个合适的模型。同时在模型选择与比较的过程中，通过模型渐进复杂程度，观察新变量在原模型上呈现出的变化，得到新模型对中国经济增长方式转变所体现的经济内涵。二是选择什么样的计量模型及估计方法才是最合适的。固定参数回归方法只是将多年的经济增长方式进行了“平均”，不能精确体现出在中国经济发展史上每个特定阶段所面临的转变特征。相对于固定参数的不足，时变参数显然能够克服此缺点。然而文献中相关时变参数模型研究均是在规模报酬不变的假设下，采用极大似然估计得到的，在规模报酬时变情况下却难以得到具有经济意义的结论，因此本文拟采用基于贝叶斯状态空间模型的MCMC算法克服极大似然估计难以收敛现象。三是选择什么样的数据才是最合适的。数据质量关系到中国经济增长方式转变结论的可靠性。本文在相关文献的基础上，采用最新的统计资料，核算出劳动力、物质资本及人力资本存量的完整时间序列数据，为研究经济增长方式转变特征提供可靠的数据支撑。

二、经济增长方式转变理论模型构建

在分析中国经济增长方式转变时，采用何种经济增长模型一直存在争议，但从实证分析文献方面来看，将Solow的希克斯中性技术进步生产函数与Lucas定义的具有人力资本要素的内生经济增长模型相结合，是中国经济增长方式转变研究的进展方向。故本文以新古典增长模型C－D函数为基准模型，逐步构建具有时变参数特征的两资模型。

（一）固定参数经济增长模型

C－D生产函数假设在希克斯中性技术进步前提下，设Y表示总产出，K表示物质资本投入，L表示劳动力投入，则其具体表达形式如下：

式（1）中，α，β分别表示资本对产出、劳动力对产出的弹性系数，即各自表达的产出效率；A（t）表示随时间t变化的技术进步；u是具有白噪声统计特征的随机扰动项。

在C－D生产函数经济增长模型基础上，如果以h表示劳动力的平均人力资本水平，然后将h乘以劳动年龄人口总量L，作为人力资本存量（也称有效劳动）的近似，这样就将原有劳动力进行了人力资本水平的“调整”，得到有效劳动生产函数模型（2），具体表达式如下：

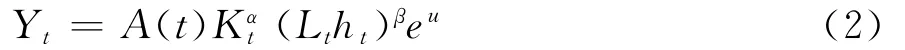
式（2）中，考虑了劳动力的质量，体现了人力资本的内涵，此时β称为人力资本弹性。另外，人力资本水平也可能对产出水平有溢出效应，因此可以在有效劳动的生产函数中引进独立的人力资本水平h，得到人力资本外部性模型（3），具体表达式如下：

式（3）中，γ为人力资本溢出效应系数，hγt为人力资本溢出效应。γ为正时表示人力资本对产出溢出效应呈现上升趋势，当γ为负时则反之。

（二）时变参数经济增长模型及TFP测算理论

现引进时变参数的建模思想，则公式（1）～（3）的生产函数形式变化为下面对应的时变生产函数形式：

公式（4）～（6）不仅体现了生产函数的弹性系数（或人力资本溢出系数）是时变的，同时也体现了规模报酬时变的特征。如果对时变规模报酬系数约束为1，则得到规模报酬不变的时变参数经济增长模型，公式（4）～（6）则相应变化如下：

为了后文叙述方便，记公式（7）～（9）对应模型为Ⅰ、Ⅱ、Ⅲ，公式（4）～（6）对应模型为Ⅳ、Ⅴ、Ⅵ。根据固定参数生产函数TFP测算的基本原理，相应模型Ⅰ－Ⅵ的TFP测算公式可归纳为如表1所示。

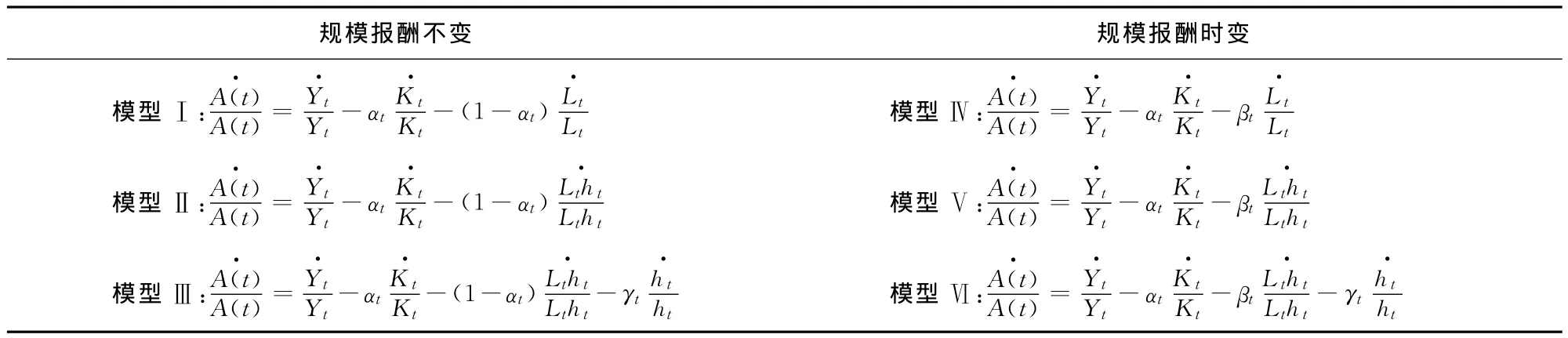
表1 时变参数增长函数的TFP测算公式

三、贝叶斯时变参数经济增长模型理论

根据研究需要，选择模型Ⅳ为研究对象，其它模型都类同于该模型的研究。该模型包含：时变参数生产函数的状态空间表示以及相应的贝叶斯推断、MCMC抽样策略。

（一）时变参数生产函数的状态空间表示

在对数线性化的模型Ⅳ中：记yt＝lnYt，at＝lnAt，lt＝lnLt，kt＝lnKt，并假设时变参数服从随机游走过程，随机扰动项服从高斯分布，则模型Ⅳ具体形式设计如下：

公式（10）～（13）中，vt、wit（i＝1，2，3）均为独立白噪声序列，其方差分别为V，Wi（i＝1，2，3）。再记，则相应的观测方程及状态方程可以分别写成下式：

观测方程为：

状态方程为：

（二）贝叶斯推断及MCMC抽样策略

1．在状态参数及数据条件下，对精度参数V－1、W－1采用Gibbs抽样

设精度参数V－1初始值的均值、方差分别为ay，by；精度参数W－1i初始值的均值、方差分别为aθi，bθi（i＝1，2，3），则精度参数V－1、W－1i可以按照下列分布进行抽样［13］：

2．在精度参数及数据条件下，对状态参数θt采用FFBS抽样

根据Carter和Kohn、Frühwirth－Schnatter提出的FFBS算法理论［13－14］，可以对状态参数向量空间进行前向滤波，后向Gibbs抽样，从而获得时变参数向量值。首先给定初始信息θ0｜D0～N（m0，C0），在前向滤波步骤中，在时刻t＝1，2，…，T－1上时对下面式（18）进行前向迭代滤波计算：

其中ht＝mt＋Bt（θt＋1－at＋1），Ht＝Ct－BtRt＋1B′t，Bt＝CtG′t＋1R－1t＋1。

四、实证结果分析

（一）数据获得及描述

本文选择数据期间为1952－2012年，跨越了61个年度。研究中涉及到四个主要变量，即：实际产出、物质资本存量、平均人力资本水平（平均受教育年限）、劳动力（原始数据来源于《新中国六十年统计资料汇编》、《中国劳动统计年鉴》及《中国统计摘要2013》）。

实际产出：先选择名义GDP作为产出指标，然后再采用1978年为基期的GDP平减指数（GDP平减指数＝本年国内生产总值／（上年度国内生产总值×本年度国内生产总值指数））进行平减获得实际产出。物质资本存量：在资产折旧率方面，王小鲁、樊纲提出了逐渐平滑加速，改变固定折旧的做法。本文物质资本存量1952－2007年的数据来源于王小鲁、樊纲的核算，2008－2012年的数据则来自核算。核算过程是首先使用固定资产投资价格指数（1978＝100）对全社会固定资产投资完成额进行平减，获得实际投资额，然后按照8%的折旧率，根据永续盘存法公式获得2008－2012年的实际物质资本存量。平均人力资本水平（平均受教育年限）：王小鲁、樊纲将人力资本存量定义为全部就业人员的受教育年限总和，并给出了具体计算公式。而平均人力资本水平（平均受教育年限）即为历年人力资本存量除以劳动年龄人口数而所得。人力资本存量1952－2007年的数据来源于王小鲁、樊纲的核算，2008－2012年的数据按照王小鲁、樊纲提供的公式进行计算。劳动力人员数及有效劳动力人员数：选择按城乡划分的年底就业人员数。由于统计口径的变化，1990年后的统计数据与前期数据存在着较大的差异，特别是1990年就业人口突增了15．5%，因此对1990－1999年的就业数据按照王小鲁、樊纲的数据进行了调整；有效劳动力人员数按照Wang和Yao的观点，将劳动力人员数乘以平均人力资本水平而获得。

（二）MCMC抽样结果及时变参数含义分析

对模型Ⅰ－Ⅵ中的每个模型进行12 000次MCMC抽样（舍去前面2 000次抽样，获得10 000次抽样结果），并经MCMC抽样的G－R统计量诊断，其值都没有超过1．2，说明MCMC抽样结果是收敛的［15］，可以进一步对时变参数所体现的含义进行探讨分析。下面首先对规模报酬不变、时变情况下的估计结果简要进行分析，然后对两类模型的合理性进行选择比较。

1．规模报酬不变的情况

在规模报酬不变的情况下，模型Ⅰ、Ⅱ、Ⅲ的时变参数、TFP值及其变化率分别如图1～6所示。

时变系数方面：图1中模型Ⅰ－Ⅲ的物质资本弹性在0．72－0．86之间。在引进有效劳动、平均人力资本水平后，模型Ⅱ、Ⅲ的物质资本弹性较模型Ⅰ的物质资本弹性变小；图2中模型Ⅰ－Ⅲ中的劳动力或有效劳动力弹性在0．14～0．28之间。在引进有效劳动、平均人力资本水平后，模型Ⅱ、Ⅲ的有劳动力弹性较模型Ⅰ的劳动力弹性上升。由此可见在规模报酬不变的情况下，考虑人力资本存量引进会使得物质资本弹性下降，劳动力资本弹性上升。图3中模型Ⅲ的时变人力资本溢出系数在20世纪50年代初到60年代中期快速下降后，然后逐渐上升，并且一直保持负值，使得人力资本溢出效应逐渐呈现下降趋势，这与中国人力资本水平的长足发展现实存在一定程度的冲突，对于这种估计结果的解释会在后面进一步讨论。

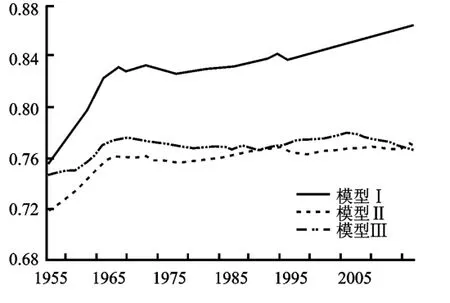
图1 时变物质资本弹性

图2 时变劳动力／人力资本弹性

图3 人力资本溢出效应情况

TFP及其增长率路径：图4中TFP值在20世纪50年代初到60年代中期逐渐曲线下降后再次逐渐曲线上升直至80年代末的小幅波动，90年代后又出现渐进曲线增长形势。在规模报酬不变的情况下模型Ⅰ、Ⅱ、Ⅲ的TFP值曲线形状大致相同，只是模型Ⅰ、Ⅲ、Ⅱ的TFP值逐渐“曲线平行”下降。图5中模型Ⅰ、Ⅱ、Ⅲ的TFP增长率在进入20世纪90年代中期后模型Ⅱ、Ⅲ的TFP增长率要稍微高于模型Ⅰ的TFP增长率，说明人力资本逐渐对TFP的增长产生作用，另外模型Ⅰ、Ⅱ、Ⅲ的TFP增长率路径与图6的经济增长路径大致相同。

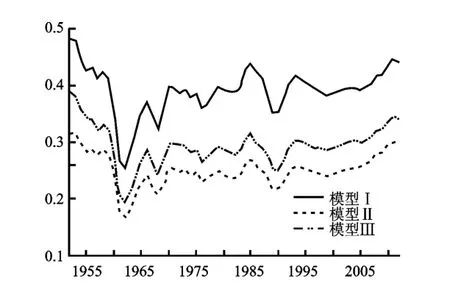
图4 TFP路径

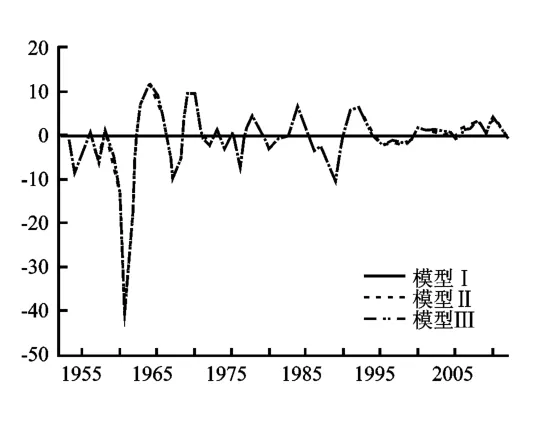
图5 TFP增长路径

图6 经济增长路径

2．规模报酬时变的情况

在规模报酬时变情况下，模型Ⅳ、Ⅴ、Ⅵ时变参数、时变规模、TFP值及其变化率分别如图7～12所示。

图7 时变物质资本弹性

时变系数方面：图7中模型Ⅳ－Ⅵ的时变物质资本弹性在0．57～0．78之间（由于作图技术要求，在保持图形位置顺序不变前提下，模型Ⅳ系数除以1．08，模型Ⅵ的系数乘以1．28）。在引入人力资本外部效应后，模型Ⅵ的物质资本弹性较模型Ⅳ、Ⅴ的物质资本弹性变小，且形状也发生了改变，前后呈现两个“V型”形状。图8中模型Ⅳ－Ⅵ的时变劳动力／人力资本弹性在0．11～0．25之间（由于作图技术要求，在保持图形位置顺序不变前提下，模型Ⅳ系数乘以1．3，模型Ⅵ的系数除以1．1），模型Ⅳ的时变劳动力弹性系数处于最下层位置，模型Ⅵ与Ⅴ的时变劳动力弹性系数依次处于第一、二的位置，同样人力资本的引进，增大了时变弹性系数。结合图7、8也可以看到模型Ⅳ中的时变物质资本弹性与劳动力弹性相差较大，而人力资本引进的模型Ⅴ、Ⅵ的两种系数较模型Ⅳ的两种系数差距减小。图9中模型Ⅳ－Ⅵ的时变规模系数在0．88～0．97之间，且系数曲线依次降低。可见即使引进人力资本，也没有改变规模报酬不变或递增的经济学假设，反而降低了规模效应。图10中模型Ⅵ的时变人力资本溢出系数在20世纪50年代初到60年代中期下降后，然后逐渐上升，并且一直保持正值，说明人力资本对产出有溢出效应且呈现上升趋势，体现了人力资本对实际产出逐渐增加的溢出效果。

图8 时变劳动力／人力资本弹性

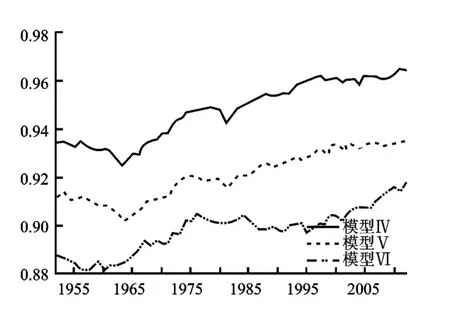
图9 时变规模效应

图10 人力资本溢出效应情况

TFP及其增长率路径方面：图11中TFP值也是在20世纪50年代初到60年代中期逐渐曲线下降后再次逐渐曲线上升直至80年代末的小幅波动，90年代后模型Ⅳ－Ⅵ的TFP路径产生了分歧，模型Ⅳ、Ⅴ的TFP值较为接近，而引用人力资本外部性的模型Ⅵ的TFP值则快速上升，说明人力资本的深化一方面在于其本身可作为一种生产要素贡献于经济的增长，另一方面在于人力资本溢出效应的存在，提高了管理效率，提升了研发技能，使得TFP值得到增加。90年代中期前的TFP增长率在规模报酬时变与不变两种情况下非常接近，但90年代中期后，规模报酬时变模型的TFP增长率要大于规模报酬不变时模型的TFP增长率。图12中在进入90年代中期后，模型Ⅵ、Ⅴ的TFP增长率比模型Ⅳ的TFP增长率逐渐增大，且3个模型的TFP增长率与经济增长路径大致相同，这均说明人力资本对TFP增长效应越来越明显。

图11 TFP路径

图12 TFP增长路径

3．规模报酬不变与时变的估计结果比较分析

时变弹性系数方面：在规模报酬不变时，一种时变弹性系数的上升必然会带来另一种时变弹性系数的下降，如图1中模型Ⅰ的物质资本弹性上升，图2中模型Ⅰ的人力资本则下降；而在规模报酬时变时，时变弹性系数则摆脱了这种约束，如20世纪90年代中期后，物质资本与人力资本（劳动力）弹性均呈现出上升趋势。另外，在规模报酬不变与时变情况下，人力资本水平的引进使得物质资本弹性减小（如图1，图7），人力资本（劳动力）弹性系数增加（如图2，图8）。结合中国经济增长方式转变的现实，一方面是物质资本的累积，另一方面是人力资本的深化，这两种资本要素对产出弹性系数都呈现上升的可能性较大，也即时变规模的假定可能更合适些。当然，这两种情况的适合性，会在后面模型的拟合效果中再进一步讨论。

人力资本溢出效应系数及溢出效应方面：在不变与时变规模报酬情况下，时变人力资本溢出效应系数分别为负值、正值，使得两种假定情况下的人力资本溢出效应对应地分别为下降、上升趋势。人力资本溢出效应发展趋势同样取决于规模报酬情况，当实际规模报酬小于1时，采用规模报酬不变的约束就会夸大资本要素对经济增长的贡献而减小人力资本的溢出效应，这种“挤出”效应的存在使得时变人力资本溢出效应系数为负值；采用时变规模报酬模型则会避免“模型误设”行为，特别当实际规模报酬不等于1时，会得到人力资本溢出效应的真实情况，时变规模报酬模型克服了不变规模报酬模型所低估的人力资本溢出效应困境。

TFP值及其增长路径方面：在规模报酬时变情况下相应模型的TFP值要比规模报酬不变情况下大（如图4、图11），这是由于实际规模报酬小于1，使得规模报酬不变的假设夸大了物质资本、人力资本（劳动力）对经济的贡献而低估了TFP值对经济的贡献，使得规模报酬不变情况下TFP值相应较小。这从侧面说明人力资本不仅本身作为一种生产要素贡献于经济的增长，还在于人力资本溢出效应的存在，使得TFP值得到增加。20世纪90年代中期前的TFP增长率在规模报酬时变与不变两种情况下非常接近，但90年代中期后，规模报酬时变情况下模型的TFP增长率要大于规模报酬不变情况下模型的TFP增长率。另外从1995年开始TFP增长率呈现连续下滑趋势，但相对于1990年代相比，最近10年来的TFP增长更趋于稳定。

4．规模报酬不变与时变模型的选择与比较

从前面时变弹性、人力资本溢出、TFP值及其增加值的分析结果来看，主要存在两个大的方面区别：一是规模报酬不变与时变情况下相应值的测度不同；二是有无人力资本存量或人力资本水平时相应值的测度不同。那么哪种结果更具有科学的依据呢？这就主要在于模型与数据、变量的融合程度，也即哪个数据、模型能够更好地说明中国产出、资本存量之间存在真实的数据机理。为此，本文引进模型拟合效果评价的平均绝对误差（MAPE）及 Theil’s U 统计量，对本文研究的6个模型估计结果做出针对性的比较与选择，其公式如下：

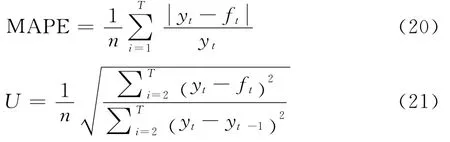
其中yt为产出，ft为样本内拟合值。当MAPE的值越小时相应拟合效果越好，Theil’s U统计量值一般小于1时拟合效果有效，当值远小于1时效果更佳。模型Ⅰ－Ⅵ的拟合效果检验如表2所示。

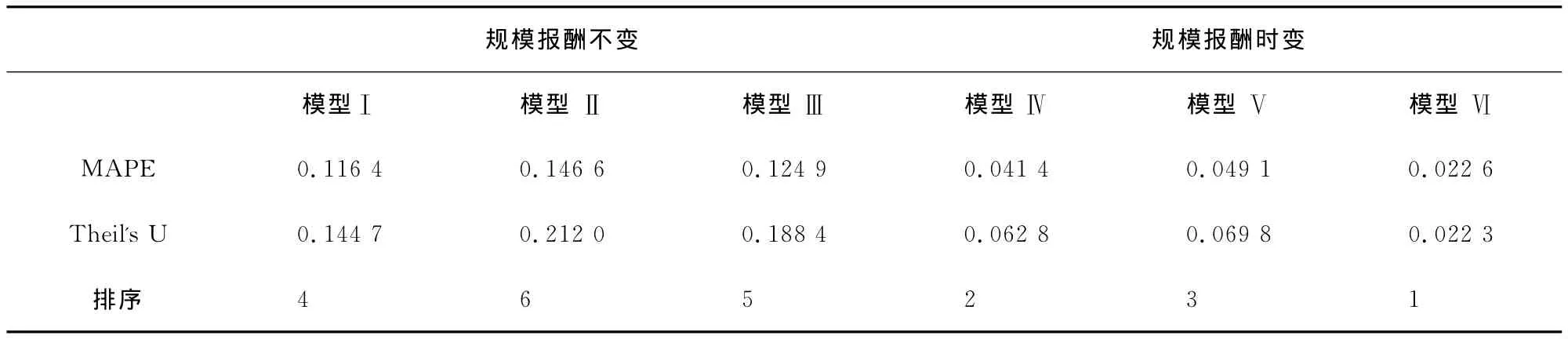
表2 6种模型拟合效果比较结果

在表2中，根据 MAPE及Theil＇sU的统计量值排序可知，规模报酬时变模型Ⅳ、Ⅴ、Ⅵ要优于规模报酬不变模型Ⅰ、Ⅱ、Ⅲ，说明规模报酬时变模型能够更好体现出中国经济转变方式的历史路径；而在规模报酬时变模型中 Ⅵ又是最好的，即时变规模效应的人力资本外部性模型是最优的，这说明人力资本作为生产要素本身为中国经济增长方式转变提供了支撑，还同时通过人力资本要素的溢出效应，促进了科学技术的进步，提高了经济管理的科学水平，转化为中国经济内源性效应增长的源泉。

五、结论及启示

本文在Solow经济增长模型以及包含人力资本的Lucas经济增长模型理论下，首先构建了规模报酬不变及时变两种类型下时变参数的C－D生产函数模型、有效劳动生产函数模型、人力资本外部性模型总共6个时变参数增长模型，然后采用核算的实际产出、物质资本存量、平均人力资本水平等数据对6个时变参数增长模型进行了贝叶斯状态空间框架下的MCMC方法抽样估计，得到了经济增长转变过程中生产要素的时变弹性、规模报酬、溢出效应、TFP值及其增长路径。本文的主要结论及启示可归纳为下面几个方面：

第一，贝叶斯状态空间模型的FFBS算法非常有效地估计出了6个模型的时变参数，估计的结果符合经济学的基本要求，克服了极大似然估计结果中的不合理现象。从拟合效果来看，时变规模报酬的3个经济增长模型比规模报酬不变的3个经济增长模型更具有刻画中国经济增长方式转变的内涵；而在时变规模报酬的3个经济增长模型中，时变参数人力资本外部性模型具有最优融合数据机理的特征，能够最好地体现中国经济增长方式转变的历史发展路径，同时也说明人力资本要素是中国经济增长方式转变不可或缺的要素，是中国经济可持续发展的重要源泉之一。

第二，时变的弹性、规模报酬、人力资本溢出现象刻画了中国经济增长方式转变的路径：物质资本弹性由于受投资周期的影响，虽然总体上呈现上升趋势，但形成路径比较曲折；人力资本弹性在进入20世纪70年代后比较稳健地呈现上升趋势，对经济增长贡献度逐渐增大；规模报酬从建国后的较低报酬逐渐呈现上升趋势，向规模报酬递增阶段迈进，这说明中国经济运行的质量和效率还需要进一步提高，才能够达到规模报酬递增的理想阶段；人力资本溢出系数及人力资本溢出效应呈现上升趋势，且现阶段人力资本溢出效应接近两个单位，这也从侧面说明如果忽略人力资本的溢出效应，必然会高估物质资本或者劳动力资本的贡献，得到规模报酬递增的结论；从时变弹性、规模报酬、人力资本溢出效应的发展路径来看，均具有不同程度的上升趋势，对经济的发展具有可持续的支撑作用。

第三，从规模报酬时变的3个序贯性建模思路来看，随着人力资本要素的引进，全要素值呈现逐渐增加趋势（如图11），全要素增长率也较其它两种模型得到的相应增长率高（如图12，且进入本世纪后TFP一直为正值），说明高质量人力资本替代简单扩张的劳动力数量后，促进了中国科技研发能力及管理水平的本质进步，这种经济增长方式的转变是来自于内源性效率的提高，比外源性效率提升的不稳定性具有更好的发展基础，这种内源性效率的提升也在中国经济可持续性发展过程中发挥重要力量。但同时也要认清一个事实，那就是TFP在进入本世纪后具有收敛性波动，与高实际经济增长率相比，TFP增长率趋势还有待改善。

总之，一方面物质资本弹性、人力资本的弹性及溢出效应具有较强上升趋势，为经济可持续增长发挥重要作用；另一方面尚未进入递增阶段的规模报酬、TFP增长率收敛性波动的现象都是现阶段需要审慎思考和解决的难题。

［1］ Solow，Robert M T．Technical Change and the Aggregate Production Function［J］．Review of Economics and Statistics，1957，39（3）．

［2］郭庆旺，贾俊雪．中国全要素生产率的估算：1979－2004［J］．经济研究，2005（6）．

［3］ Lucas R E．On the Mechanics of Economic Development［J］．Journal of Monetary Economics，1988，22（1）．

［4］ Yan WANG，Yudong Yao．Sources of China’s Economic Growth 1952－1999：Incorporating Human Capital Accumulation［J］．China Economic Review，2003，14（1）．

［5］景跃军，刘晓红．基于卢卡斯溢出模型的中国人力资本对经济增长贡献率测算［J］．东南学术，2013（1）．

［6］汤向俊．资本深化、人力资本积累与中国经济持续增长［J］．世界经济，2006（8）．

［7］高宇明，齐中英．基于时变参数的中国全要素生产率估计［J］．数量经济技术经济研究，2008（2）．

［8］陈娟．全要素生产率对中国经济增长方式的实证研究［J］．数理统计与管理，2009（3）．

［9］章上峰，许冰．时变弹性生产函数与全要素生产率［J］．经济学（季刊），2009（2）．

［10］王小鲁，樊纲．中国经济增长的可持续性——跨世纪的回顾与展望［M］．北京：经济科学出版社，2000．

［11］Chow G C．Capital Formation and Economic Growth in China［J］．Quarterly Journal of Economics，1993，108（3）．