运用变点理论对连涨连跌收益率的Bayes分析

黄 飞， 谭常春

（合肥工业大学 数学学院，安徽 合肥 230009）

0 引 言

随着经济的不断发展，人们对股市的研究越来越多，其中金融资产收益率成为重要的关注点之一，并取得了一定的研究成果。文献［1］通过修正的Weibull分布对中国股市收益率的分布状况进行了研究；文献［2］结合上海证劵市场的特点，对上证综指股收益率的波动特点进行了分析。以往研究的收益率一般是每日收益率，也有关于连涨和连跌收益率的研究，文献［3］通过生存分析与变点理论对深证成指进行了研究，发现连涨和连跌的股指收益率服从伽玛分布，并对深证成指连涨和连跌的收益率作了变点检验；文献［4］运用生存分析与变点理论对上证指数进行了研究，发现了股指在不同的政策时期其上涨和下跌的概率是不同的；文献［5］基于Copula－ACD模型对股票连涨和连跌收益率作了风险分析。

变点问题最初始于Page在1954年发表的一篇关于连续抽样检验的文章，它广泛应用于工业质量控制、经济、金融等领域。研究变点问题的方法［6－7］有很多，如极大似然法、累计次数法、Bayes法。Bayes方法对于解决假设检验问题，根本的出发点是后验分布。文献［8］研究了 Weibull分布刻度参数经验Bayes检验问题，其中采用Bayes法对变点问题的研究比较多，如在指数族分布中；文献［9］运用贝叶斯分析的方法估计独立随机变量序列的变点，并且将这一方法应用到尼罗河流量问题、煤矿事故、交通事故以及股市价格问题上；文献［10］研究了变点的后验分布的渐近性；文献［11］运用Bayes法估计了指数族参数变点的位置。

本文采用Bayes法研究上证指数连涨和连跌收益率变结构问题。文中以2005年6月6日至2010年5月12日的上证指数作为研究对象，主要运用Bayes法检验是否有变点存在，当有变点存在时估计上证指数波动起伏变化的位置具有重要的意义，直接关系到证劵组合选择的正确性、风险管理的有效性及期权定价的合理性。

1 上证指数连涨连跌的理论分布的估计

（1）数据描述。由于2005年6月6日至2007年10月16日是中国目前最大的一轮牛市，从998涨至6 040点。自2007年10月16日以后又一路下跌，跌至5 000、4 000、3 000、2 000点，后长期盘整，这段时间上证指数的起伏波动比较大。对近期上证指数进行研究有利于考虑相关政策的实施对股市的影响，从而指引中国股市正常运转。因此选取这段时间的上证指数作为研究对象。

2005年6月6日至2010年5月12日共1 204个交易日的上证指数的走势如图1所示。

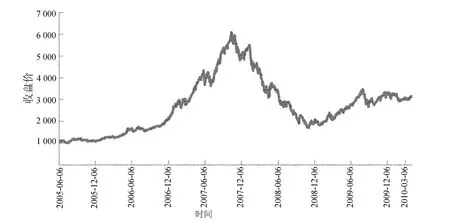
图1 上证指数（2005年6月6日至2010年5月12日）

（2）连涨连跌收益率的简单描述。设Rt为每日收益率，Pt为每日收盘价，则有：

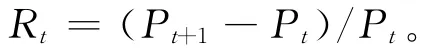
在每日收益率的基础上，统计这1 204个交易日收盘价每次从开始上涨至上涨结束时收益率的和，即连涨的收益率；统计每次开始下跌至下跌结束时收益率的和，即连跌的收益率。共得到连涨的收益率序列297个和连跌的收益率序列297个，同时记连涨的收益率为X和连跌的收益率为Y，所得连涨和连跌收益率见表1所列。

（3）阶段划分。由于数据太多无法对连涨连跌收益率作Bayes实证分析，必须进行分段考虑。在这期间中国股市有几个政策发布，2005年6月6日证监会推出《上市公司回购社会公众股份管理办法（试行）》，该天股指跌破千点；2007年5月30日证劵交易印花税税率进行调整；2008年10月12日受到金融危机的影响，财政部、中央汇金公司、国资委采取了一些有利的措施。因此将1 204个交易日的上证指数分成以下3个阶段进行研究：①2005年6月6日至2007年2月2日；②2007年2月5日至2008年10月9日；③2008年10月10日至2010年5月12日。

（4）K－S检验。利用 K－S检验对2005年6月6日至2010年5月12日这3个阶段的连涨和连跌收益率进行了拟合优越度检验，检验结果见表2所列。

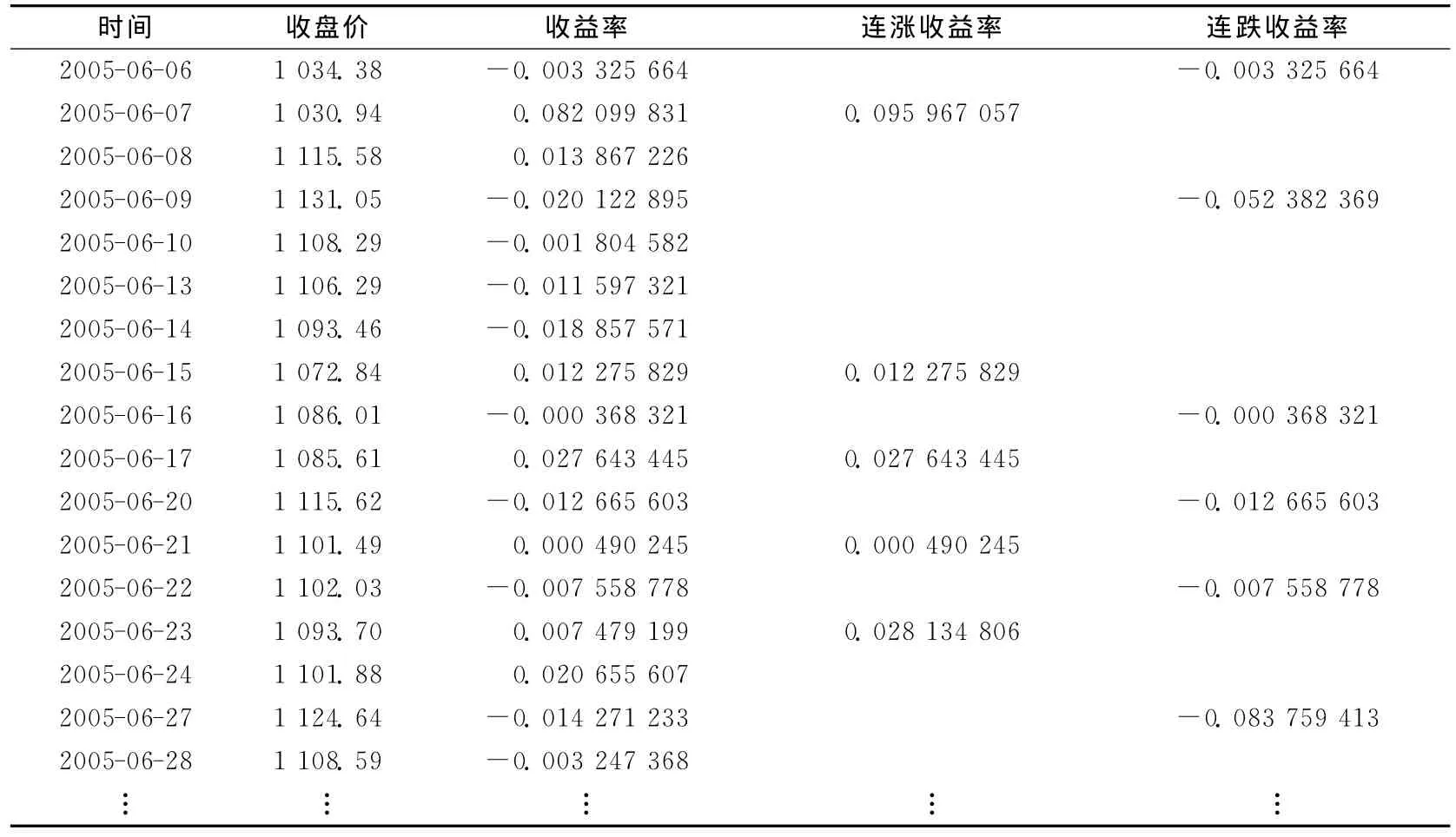
表1 2005年6月6日至2010年5月12日连涨连跌收益率

表2 3个阶段拟合优越度检验结果

从K－S拟合优越度检验研究可以看出，上证指数的连涨和连跌的收益率服从伽马分布（并不是无记忆的指数分布），表明股市是有记忆的，换句话说，股票价格的变动受到以前价格的影响。

2 伽马分布变点的实证研究

2.1 Bayes方法介绍

设总体X服从Γ分布，其概率密度函数为：

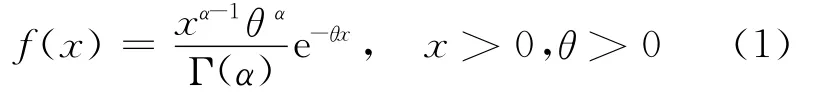
化简得：

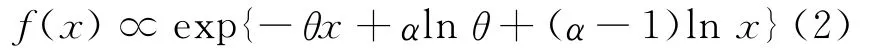
将（2）式记为Γ（α，θ），其中，α为形状参数；θ为刻度参数。记Fθ为其分布函数。

Bayes法的主要工作内容如下：① 检验是否有变点存在（H0：j＝n↔H1：j≠n）；② 当有变点存在时估计变点的位置，其中如何求变点j的后验分布是关键。利用先验分布与样本分布，可以求出变点这个参数的后验分布，并基于其做出所要的推断。应用文献［9］中指数族变点j的后验分布结果可得：

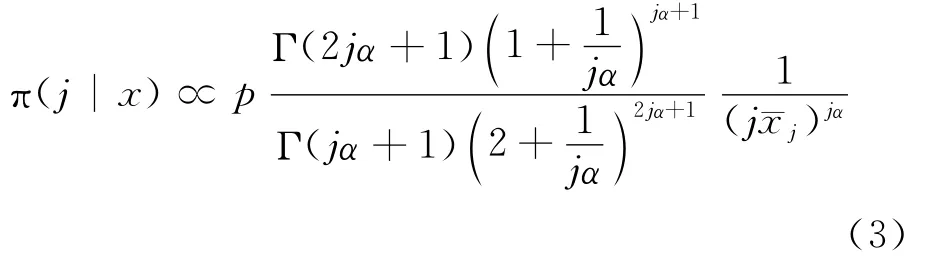
其中，j＝n。

其中，j＝1，…，n－1。

2.2 实证分析

由于这3个阶段的上证指数连涨连跌收益率服从Γ分布，可以应用Bayes的方法对伽马分布作变点检验。

首先对第1阶段的上证指数连涨收益率作变点检验，得到连涨的收益率序列102个，由表2知Xi～Γ（1.066，0.024）。

为了检验是否有变点存在，令p＝0.5（即先验对有无变点没有任何倾向性），由（3）式可得，给定的连涨收益率序列X1，X2，…，Xn，j＝n的后验概率p（j＝n｜x）＝6.36E－8以及Bayes因子为6.36E－8。已知Bayes因子反映的是样本对原假设H0支持的程度，其值越大，则H0成立的可能性越大；其值越小，则H1成立的可能性越小。它表明对连涨的收益率作检验时，第1阶段存在显著性的变点。

为了估计变点的位置，令p＝0（即j＝n的概率为0），利用（4）式，可获得取定各类变点情形时的后验概率，其中k为变点取的位置，k＝1，2，…，102。所得结果见表3所列。

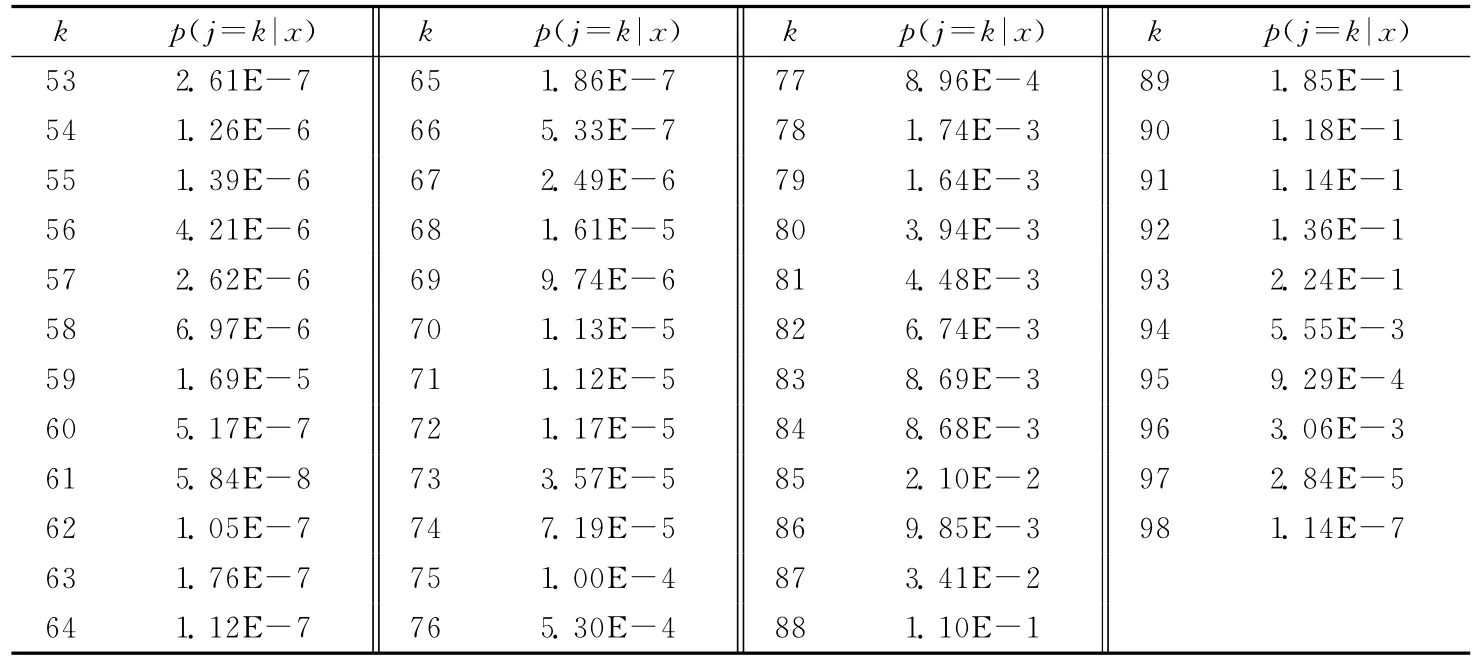
表3 变点j的后验概率

由表3不难发现，对于给定的连涨收益率序列X1，X2，…，Xn，j＝93的后验概率2.24E－1远大于其他各点处值，它表明变点发生在j＝93这一位置，即在2006年12月21日附近。水平为0.05的最大后验密度可信集为：

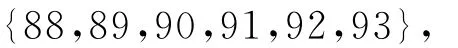
它包括6个点。

同样的方法可以得到第1阶段连跌的收益率取定各类变点情形时的后验概率，连同连涨收益率各类变点的后验概率，如图2a所示。

第2阶段关于连涨和连跌的收益率取定各类变点情形时的后验概率如图2b所示。

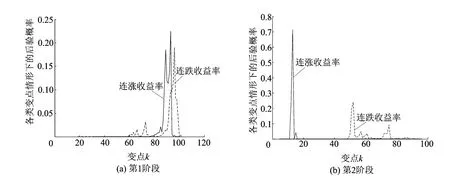
图2 第1阶段、第2阶段连涨、连跌收益率各类变点情形的后验概率

对第1阶段的连涨收益率作检验，连涨收益率所对应的伽马分布的形状参数为1.066，大于1，而连跌收益率所对应的伽马分布的形状参数为0.844，小于1，表明该阶段的股市处于牛市，以5%的显著性水平，得到参数的一个显著性变点，即2006年12月21日附近。同时对第1阶段的连跌收益率作检验，同样得到1个变点，即在2006年12月6日附近，这与连涨的收益率的变点检验基本吻合。

对第2阶段的连涨收益率作检验，以5%的显著性水平，得到参数的1个显著性变点，即2007年5月15日附近，这大约正好处于2007年5月30日证劵交易印花税税率调整时候，在此背景下，上海股市产生了具有下跌趋势的变点。对第2阶段的连跌收益率作检验，同样得到1个变点，即在2008年1月14日附近。

关于第3阶段关于连涨和连跌的收益率取定 各类变点情形时的后验概率如图3所示。

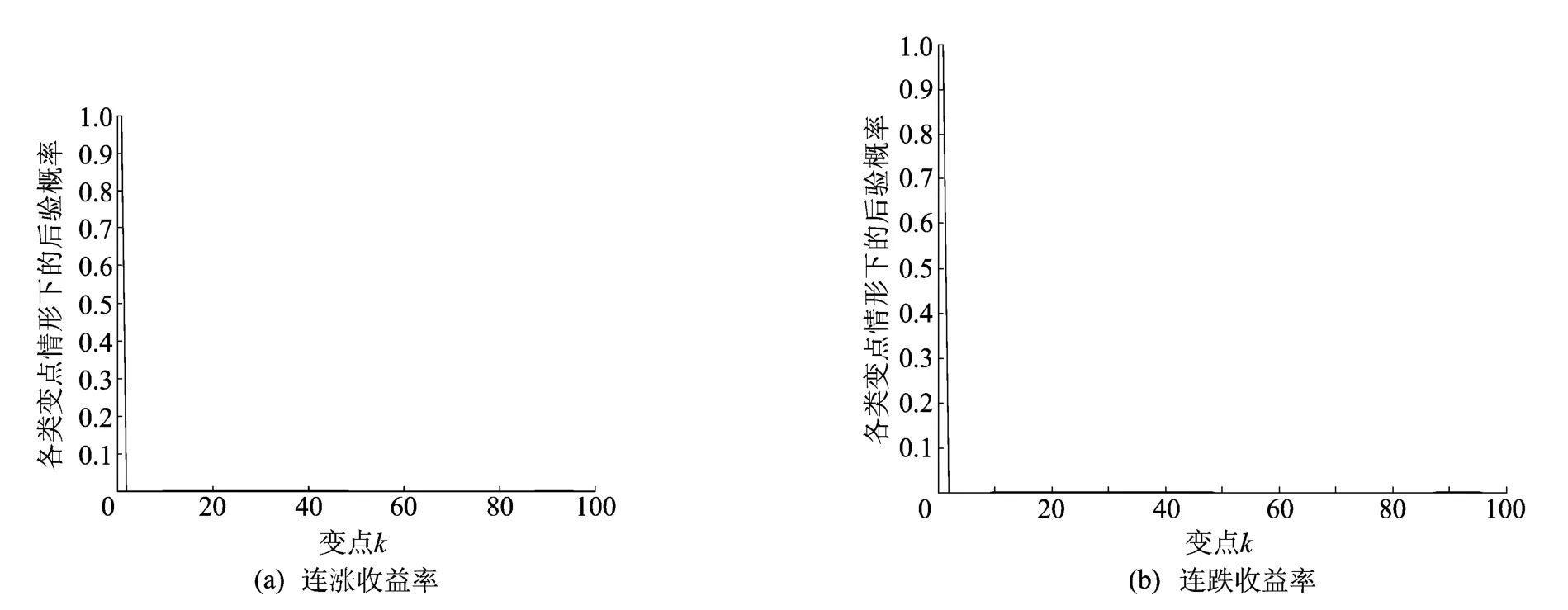
图3 第3阶段连涨、连跌收益率各类变点情形的后验概率

由图3a可知，k＝1的后验概率非常大，而k为其他值时均小于0.1。显然，以5%的显著性水平，可以得到参数的1个显著性变点，即在2008年10月10日附近。由图3b可知，对连跌的收益率作检验，同样的在2008年10月10日附近得到1个变点，这与连涨收益率的变点检验基本吻合。2008年10月12日金融危机爆发，中国推出一系列救市政策，如面向房地产等市场。正因为如此，大量的资金入市，最终汇集到股市里。这表明2008的金融危机对上海股市的影响很大。

结合Bayes的方法，对2005—2010年上证指数作了实证分析，发现国家政策的调整会导致股市的变化。

3 结束语

综上所述可以看出，变点发生的时间与国家政策的发布存在着一定的关系。本文研究结果表明，用K－S检验上证指数的连涨和连跌收益率发现其服从伽马分布，而且拟合的效果很理想。运用Bayes法对上证指数连涨和连跌收益率进行实证分析，判断了上证指数是否有变点存在以及当有变点存在时确定的变点位置，这有利于分析股市的变化。但是，如果按照所求变点的位置重新对这段时间的上证指数划分区段，得到的P值应当更高。

［1］ 卢方元.中国股市收益率分布特征实证研究［J］.统计与决策，2004，12（6）：100－101.

［2］ 陈圆圆.上证综指股票收益率波动特点分析：基于GARCH模型［J］.现代商贸工业，2012（6）：114－116.

［3］ 雷 鸣，谭常春.运用生存分析与变点理论对深证成指的研究［J］.产业经济研究，2008，7（6）：73－78.

［4］ 雷 鸣，谭常春，缪柏其.运用生存分析与变点理论对上证指数的研究［J］.中国管理科学，2007，15（5）：3－10.

［5］ 胡心瀚，叶五一，缪柏其.基于Copula－ACD模型的股票连涨和连跌收益率风险分析［J］.系统工程理论与实践，2010，30（2）：108－114.

［6］ 陈希孺.变点统计分析简介［J］.数理统计与管理，1991，10（1）：55－58.

［7］ 陈希孺.变点统计分析简介：Ⅲ 极大似然法、累计次数法、Bayes法［J］.数理统计与管理，1991，10（3）：52－59.

［8］ 黄金超，凌能祥.威布尔分布族参数的经验Bayes检验［J］.合肥工业大学学报：自然科学版，2012，35（6）：860－864.

［9］ Lee C B.Bayesian analysis of a change－point in exponential families with applications ［J］.Computational Statistics ＆Data Analysis，1998，27（2）：195－208.

［10］ Rukhin A L.Asymptotic behavior of posterior distribution of the change－point parameter ［J］.Journal of Statistical Planning and Inference，2002，105（2）：327－345.

［11］ Ghorbanzadeh D，Lounes R.Bayesian analysis for detecting a change in exponential family ［J］.Applied Mathematics and Computation，2001，124（1）：1－15.