基于GHM多小波和神经网络的小电流接地故障选线

牛敬芳， 肖本贤

（合肥工业大学 电气与自动化工程学院，安徽 合肥 230009）

我国6～66kV配电网多数为小电流接地系统，小电流接地系统发生单相接地故障时，由于故障电流很小，因此，故障的判定一直是业内的一大难题。目前，国内的选线装置主要有利用稳态信号的选线方法［1］，如零序电流幅值比较法、零序电流方向法、谐波分量法、注入信号寻迹法；利用暂态信号的选线方法，如首半波法、暂态法、行波法等。但由于故障稳态分量太小，而且采用稳态分量的方法要求短路时必须有各个稳态的过程，因此也不适用于发生间歇性电弧接地的系统。故障暂态信号虽然幅值比稳态信号大，但是由于其持续时间短，有时很难捕捉到暂态信号，所以小电流接地故障选线一直没有比较理想的方法［2］，由此出现了综合利用故障稳态和暂态信号进行选线的方法，如基于小波变换和神经网络技术的方法近年来得到了广泛的研究与应用［3－5］。

传统的小波是由一个尺度函数构成的小波，也称单小波，理论已证明，在实数域中，同时具有紧支撑、对称性和正交性的非平凡单小波是不存在的［6］，由此限制了单小波的应用。多小波理论是小波理论的发展，多小波是2个或2个以上尺度函数构成的小波，因而多小波具有更好的特性，可以同时具有对称性、正交性、短支撑和高阶消失矩等特性［7］，因此基于多小波与神经网络的故障选线方法能够从故障信息中提取更丰富的信息，从而实现对故障信号更精细的逼近［8－9］。著名的GHM多小波作为典型的多小波也得到了广泛的研究与应用，利用GHM多小波和神经网络相结合的方法实现小电流接地故障选线的方法［10］，比传统的检测方法更具有适应性，判断结果更准确。

1 多小波分析

1.1 多小波的Mallat算法

多小波的多分辨率分析是对单小波的多分辨率分析的推广，可以依据单小波的多分辨率分析，并将其扩展到R维，从而可以得到R重多小波的R重多分辨分析。根据多小波的多分辨率分析可以得到多小波的双尺度方程为［11］：

其中，Hk、Gk为多小波滤波器组。若令：

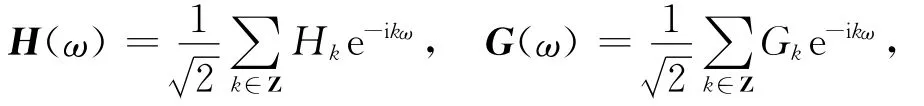
则有双尺度方程的频域形式：

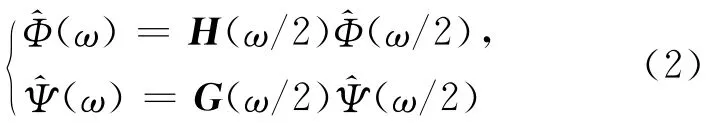
其中，H（ω）为矩阵低通滤波器组；G（ω）为矩阵高通滤波器组。类似单小波，对于f（t）∈V0≈L2（R），可在正交多分辨率分析中展开：

其中

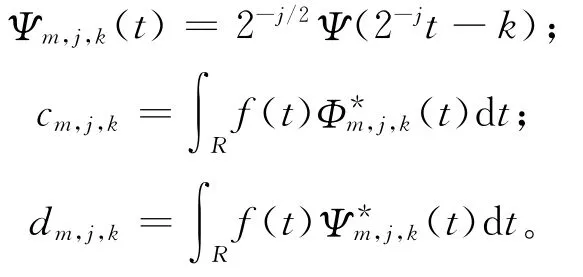
若令：dj，k＝（d1，j，k，d2，j，k，…，dr，j，k）T，cj，k＝（c1，j，k，c2，j，k，…，cr，j，k）T，则由双尺度方程可得：

r维矢量｛cj，k｝j∈Z称为离散多小波变换，（4）～（6）式分别为多小波的分解与重构公式，该算法也称作多小波的Mallat算法。

1.2 GHM 多小波

GHM多尺度函数Φ1、Φ2和多小波函数Ψ1、Ψ2的时域波形如图1所示。

Φ1、Φ2的支撑长度分别为［0，1］、［0，2］，Ψ1、Ψ2的支撑长度都为［0，2］，GHM多小波具有实值对称与反对称性、正交性、紧支撑和二阶消失矩。GHM多小波滤波器的系数矩阵为［11］：

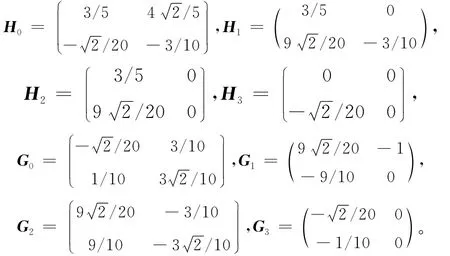
图1 GHM多尺度函数Φ1、Φ2和多小波函数Ψ1、Ψ2的时域波形

对于多小波而言，关键的问题是预处理［4］。一方面，进行原始信号预处理对所有多小波分析是必须的，因为一般情况下原始信号是一维的，而多小波的尺度函数和小波函数是多维的；另一方面，采用不同的预处理方法对于多小波的处理效果影响非常大。多小波的预处理方法一般分为预滤波方法和采用平衡多小波的方法。对于预滤波方法的研究主要集中在GHM预滤波的研究方面。对于两维多小波的预处理方法有2种：

（1）直接复制原数据从而得到两维完全相同的数据，然后进入Mallat分解。

（2）构建1组预滤波器和后滤波器，首先将原始数据通过预滤波器使其输出为两维数据，然后通过后滤波器恢复为原维数。本文采用第1种方法，计算相对简单。

2 实验模型的构造

2.1 能量特征向量的构造

根据多小波Mallat算法分析，由Parseval定理可以得到：

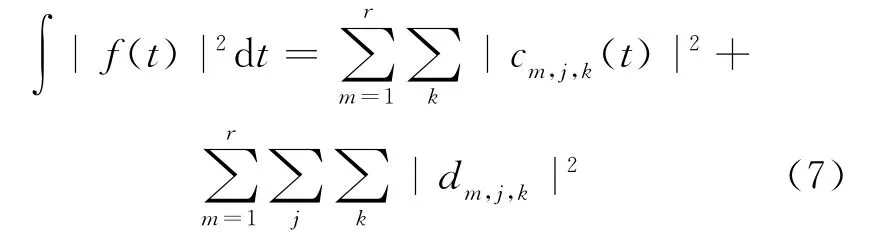
由以上分析可知，通过多小波Mallat算法，可以得到故障信号的近似系数和细节系数，通过这些多小波系数，由（7）式计算出信号的能量。将信号的能量表示为特征向量的表达式：

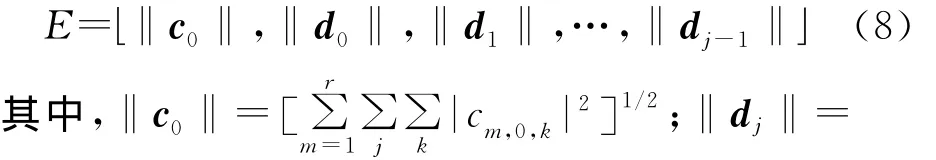
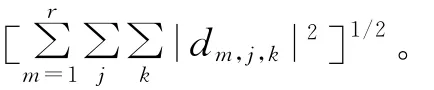
综上所述，得到小电流故障选线的原理如下：检测线路的零序电压，根据发生小电流接地故障时的零序电压比非故障时大倍，分别测量线路正常运行和线路故障时的电流信号，根据上述分析分别得到线路正常运行和故障时的能量特征向量，比较各条线路的能量变化大小，若各条线路的能量变化均不超过选定的门槛，则视为母线故障，否则，选择能量变化最大的线路为故障线路。

2.2 小电流接地仿真模型的构造

利用Simulink建立实验仿真模型如图2所示，模型共有3条线路，线路1、线路2的长度均为100km，其中线路3的A相发生接地故障，通过设定不同的接地电阻、相位和故障点的位置分别进行仿真。

设置接地电阻分别为 0.001、0.01、0.1、1、10、50、100、200、300、400、500、1 000Ω，故障发生的时间分别为0.04～0.1s、0.02～0.08s，线路3的长度分别为100、200、300km，则共得到216组仿真数据。

图2 小电流接地实验仿真模型

3 实验结果分析

将通过仿真模型得到的216组仿真数据，利用构造的GHM多小波进行Mallat分解，利用（7）式、（8）式构造故障能量特征向量，选取部分能量特征向量见表1所列。

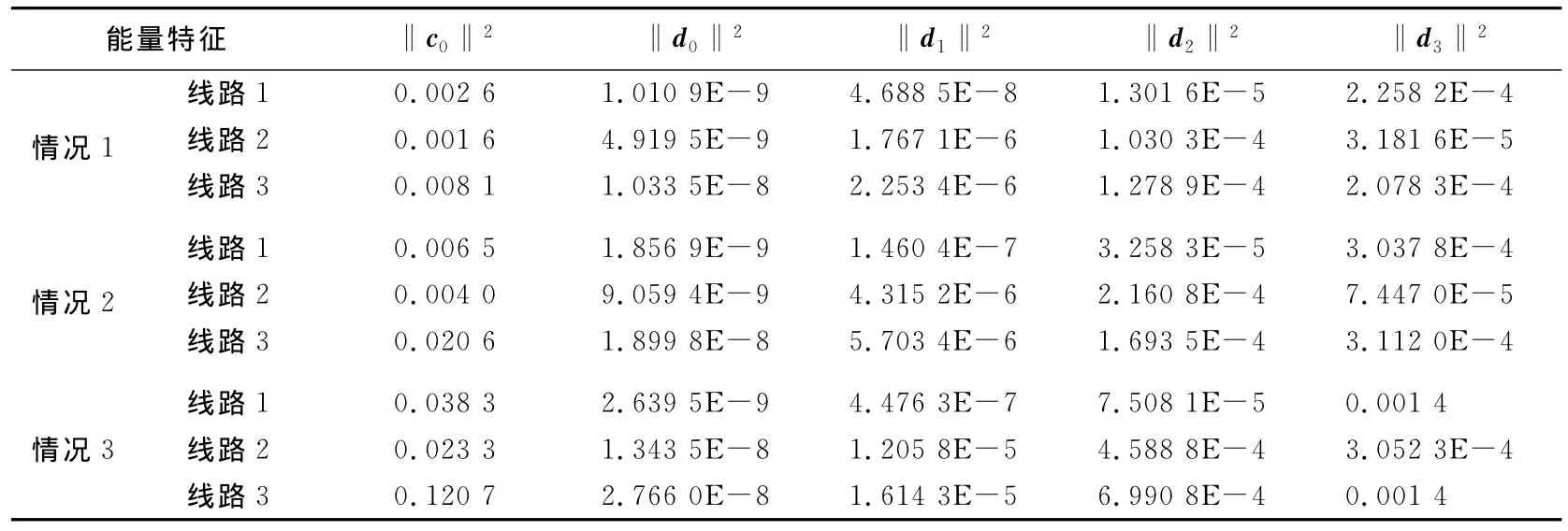
表1 能量特征向量

将仿真计算出的216组能量特征向量送给神经网络［7－8］，神经网络选用经典的BP神经网络，其中152组作为训练数据，64组作为测试数据。神经网络输入为3个8维的能量特征向量，隐含层设为12层，输出为3维的向量，神经网络训练迭代次数为100，训练目标设为0.001，学习率设为0.1。对其进行训练，经过30个迭代周期即可得到训练误差为0.000 413 9，则得到64组测试数据的理想输出与实际输出误差如图3所示。

若用传统小波D4代替GHM多小波，则得到64组测试数据的理想输出与实际输出误差如图4所示。

上述3种情况的理想输出与实际输出见表2所列，仿真结果证明了该方法的可行性和准确性。

图3 多小波与神经网络预测误差

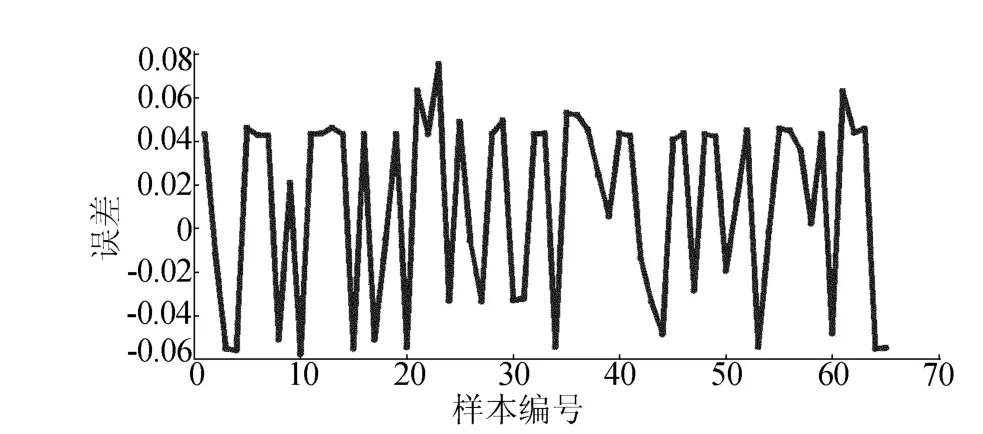
图4 小波与神经网络预测误差

经过统计可知，采用单小波选线的正确率为90.475%，而采用多小波选线的正确率可达98.987%。

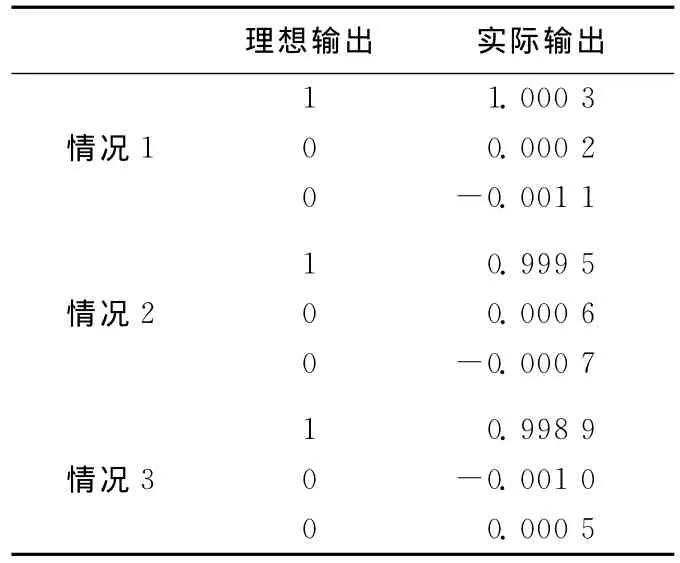
表2 理想输出与实际输出对比

4 结束语

小电流接地故障选线问题在我国配电网中一直非常重要，本文将多小波理论与神经网络相结合应用于小电流接地故障选线，是一种充分利用了小电流接地故障时的稳态特征和暂态特征的方法，比传统的方法具有突破性，与基于传统单小波与神经网络相结合的方法相比，该方法充分利用了多小波的优势，能够从故障信息中提取更丰富的信息，从而实现对故障信号更精细的逼近，因而判断结果更准确。但是该方法比传统的方法更复杂，计算量更大。

［1］ 郭清滔，吴 田.小电流接地系统故障选线方法综述［J］.电力系统保护与控制，2010，38（2）：146－152.

［2］ 陈 奎，唐 轶.小电流接地系统单相接地故障选线的研究［J］.高电压技术，2007，33（11）：180－184.

［3］ Liu Zhigang，Li Wenfan，Sun Wanlu.A novel method of short－term load forecasting based on multiwavelet transform and multiple neural networks［J］.Neural Computering＆ Applications，2013，22（2）：271－277.

［4］ Gong Lin chun，Huang Zhixiong.Study on fault location for distribution lines based on wavelet fuzzy neural network［J］.Electric Power，2008，41（2）：26－34.

［5］ 黄肇明，钟 诚，黎小如.基于BP神经网络的呼吸系统疾病诊断仿真研究［J］.合肥工业大学学报：自然科学版，2012，35（3）：347－349.

［6］ 程正兴，杨守志，张玲玲，等.多小波理论的发展与研究［J］.工程数学学报，2001，18（5）：1－16.

［7］ Li Bo.Technology of fault line selection for single－phase－to－earth fault in small current grounding system［J］.Nonlinear Dynamics，2012，67（3）：2111－2122.

［8］ 庄哲民，殷国华，李芬兰，等.基于小波神经网络的风力发电机故障诊断［J］.电工技术学报，2009，24（4）：224－228.

［9］ 林美琴，陈艳峰.基于多小波变换的模拟电路IDDT故障诊断［J］.计算机工程与应用，2009，45（23）：239－241.

［10］ 李文军.多小波和小波神经网络构造及其在电弧故障诊断中的应用研究［D］.吉林：吉林大学，2008.

［11］ Özkaramanli H.Multi－wavelets from B－spline super－functions with approximation order［J］.Signal Processing，2002，82（8）：1029－1046.