基于演化博弈的产业共生行为的研究

2014-12-31冯南平占李桢

合肥工业大学学报（自然科学版） 2014年2期

冯南平，占李桢，张璐

（1.合肥工业大学管理学院，安徽合肥 230009；2.合肥工业大学产业转移与创新发展研究中心，安徽合肥 230009）

上游企业产生的废物作为生产原材料提供给下游企业，从而通过资源的循环利用达到减少工业发展对生态环境影响的产业生态系统（industrial ecosystem，简称IES）［1－2］是循环经济最终实现的关键［3］。然而伴随着产业生态系统实践活动规模的快速扩大，诸多问题在实际运营过程中逐渐暴露出来，其中稳定性问题最为突出。包括被世界公推为典范的卡伦堡共生体在内的一些生态产业系统，在运营过程中都曾出现过生态产业链条的断裂、变动，甚至整个系统崩溃。因此，产业生态系统稳定性对于产业生态系统维持良好运转并获得成功起着至关重要的作用［4］。

演化博弈论是把动态演化过程分析和博弈理论分析结合起来的一种新理论，有限理性及信息不对称是其区别于传统博弈理论的重要方面，在理论和实践2个方面都有着重要意义［5］。近年来，演化博弈论已经成为经济学研究中的重要研究方法，经济学家们运用演化博弈论分析社会习惯、规范、制度或体制形成的影响因素，解释其形成过程，并产生了大量的研究成果［6－8］。

产业生态系统中的企业是参与博弈的博弈主体，它的策略选择具有限理性、不确定性、路径依赖和事件不可逆等特点，这就表明博弈主体之间的策略均衡是通过动态的调整过程达到的结果，而非一次性选择的结果。因而采用演化博弈的思想研究产业生态系统中企业的共生行为策略演化机制，比在完全理性基础上的博弈分析方法更具有现实意义。现有文献关于产业生态系统的产业共生行为研究，一般多从静态角度进行分析，而实际产业的共生行为是一个动态的均衡实现和保持过程，采用演化博弈的方法研究产业共生行为是本文的创新点。

基于此，本文从演化博弈角度研究产业生态系统中产业的共生行为策略演化机制，分析影响参与主体策略选择的影响因素，构建各参与主体的支付函数，并建立相应的复制动态方程，寻求演化稳定策略，最后对演化博弈模型进行分析，并给出各影响因素对模型中初始状态的作用机理。

1 产业共生机制的演化博弈模型建立

演化博弈的核心是演化稳定策略和复制动态方程［9］，复制动态方程是描述某一特定策略在一个参与主体中被采用的频数或频度的动态微分方程。根据演化原理，一种策略的收益或支付比种群的平均适应度高，这种策略就会在种群中发展（即适者生存），体现在这种策略的增长率（复制动态方程）大于0，则有：

其中，XK为采用策略K时的比例；S的取值范围为1～K；E（K，S）为采用策略K时的适应度；E（S，S）为平均适应度；K为策略总数。对于演化稳定策略的K，需满足F（XK）＝0及F′（XK）＜0，在建立支付矩阵之前，作如下假设。

（1）IES中的企业均为有限理性和信息不对称，这是由参与人之间的差异性、经济环境及博弈问题本身的复杂性所导致的［10］。

（2）博弈主体以个体利益最大为目标，其中利益包含企业的经济效益和环境效益等方面。

（3）企业之间的合作是产业生态系统存在的基本合作单元，因此，考虑产业生态链上的2个合作企业群体代表企业群体A和企业群体B为博弈的主体，且企业群体A作为产业生态链中的上游企业群体，提供生产过程中产生的副产品或废弃物，企业群体B作为企业群体A的下游企业，接受企业群体A提供的副产品或废弃物作为生产所需的部分原材料来源。其中作为某条产业生态链中的上游企业，即该企业处于企业群体A中，它在其他产业生态链上可能为下游企业，则该企业处于企业群体B中。而作为某条产业生态链上的下游企业，即该企业处于企业群体B中，它在其他产业生态链上可能为上游企业，则该企业处于企业群体A中。产业生态链中企业之间的共生关系如图1所示，此博弈模型中博弈主体的策略集合为共生、不共生。

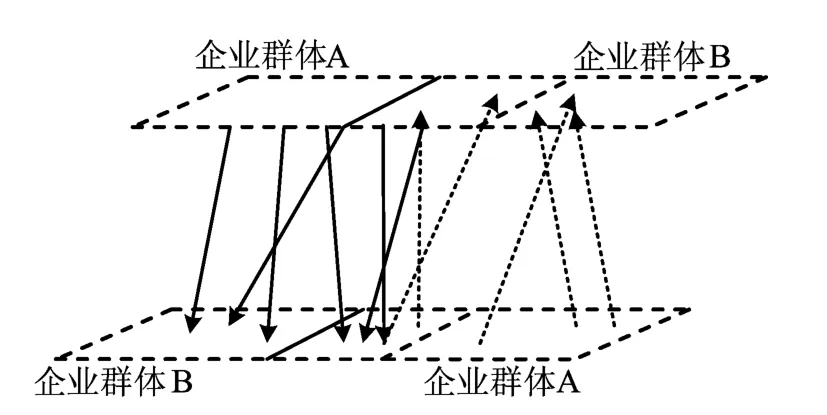
图1 博弈主体关系示意图

（4）假设企业A提供给企业B的副产品或废弃物的总量为K，经双方协商废弃物的交易价格为V1，企业B从外界采购原材料的交易价格为V2，显然有V2＞V1。企业之间建立合作关系所需的设备、技术等成本为C，且由企业A与企业B共同承担，分摊系数为α、β，其中α＋β＝1。当企业A选择不共生策略时，将对废弃物或副产品进行处理后再排放到环境中，其中所产生的处理费用或政府收取的环境污染治理费用为W，企业群体A中采取共生策略的博弈方比例为PA，企业群体B中采取共生策略的博弈方比例为PB。根据以上假设，构造企业群体A及企业群体B在机会主义下及惩罚机制下的机会主义博弈支付矩阵，分别见表1、表2所列。

表1 机会主义下的博弈支付矩阵

表2 惩罚机制下的博弈支付矩阵

（5）若考虑第三方监管机构建立的惩罚机制，即建立共生关系后，若博弈主体中有一方撤出共生关系链，则撤出方必须承担部分损失，假设损失的费用与投入的成本C成正比，比例系数为λ。在企业与第三方监管机构博弈的模型中，假设采取共生策略的企业获得的总收益为ΔV，第三方监管机构的监督成本为f。企业中采取共生策略的博弈方的比例为P，监管机构执行监督的概率为q，根据以上假设，构造企业与监管机构的博弈支付矩阵，见表3所列。

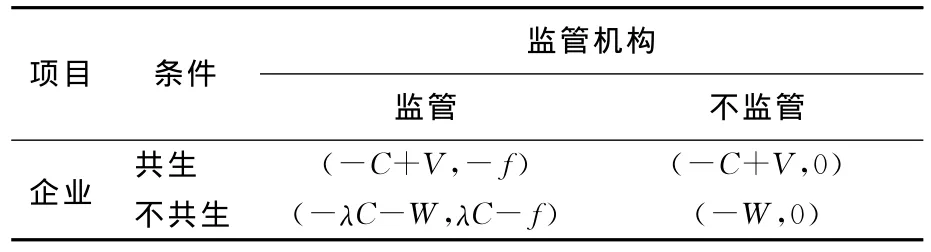
表3 企业与监管方的博弈支付矩阵

1.1 机会主义行为策略的演化博弈模型

根据机会主义下企业策略的博弈支付矩阵，可得到双方在不同策略下的适应度。企业群体A中采取共生策略的适应度为PB（－αC＋V1K）＋（1－PB）（－C－W），企业群体A中采取不共生策略的适应度为PB（－W）＋（1－PB）（－W），故其平均适应度为PA（βCPB＋V1KPB－C－W＋WPB）＋（1－PA）（－W）。

企业群体B中采取共生策略的适应度为PA（－βC－V1K）＋（1－PA）（－C－V2K）），企业群体B中采取不共生策略的适应度为PA（－V2K）＋（1－PA）（－V2K），故其平均适应度为PB（αCPA＋（V2－V1）KPA－C－V2K）＋（1－PB）（－V2K）。

根据复制动态方程定义，可得机会主义下产业共生行为策略的复制动态方程为：

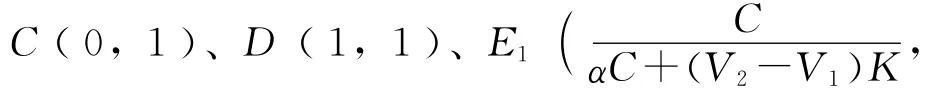
图2 机会主义下群体A的复制动态相位图

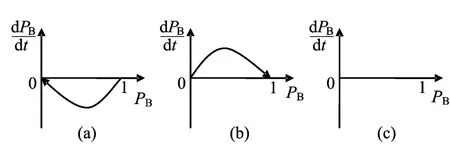
图3 机会主义下群体B的复制动态相位图

1.2 惩罚机制下行为策略的演化博弈模型

根据惩罚机制下企业策略的博弈支付矩阵，可以得到双方在不同策略下的适应度。

惩罚机制下企业群体A中采取共生策略的适应度为PB（－αC＋V1K）＋（1－PB）（－C－W），企业群体A中采取不共生策略的适应度为PB（－W－λC）＋（1－PB）（－W－λC），故其平均适应度为PA［（1－α）CPB＋V1KPB－C－W＋WPB］＋（1－PA）（－W－λC）。

惩罚机制下企业群体B中采取共生策略的适应度为PA（－βC－V1K）＋（1－PA）（－CV2K），企业群体B中采取不共生策略的适应度为PA（－V2K－λC）＋（1－PA）（－V2K－λC），故其平均适应度为PB［αCPA＋（V2－V1）KPA－CV2K］＋（1－PB）（－V2K－λC）。

根据复制动态方程定义，可得惩罚机制下产业共生行为策略的复制动态方程为：

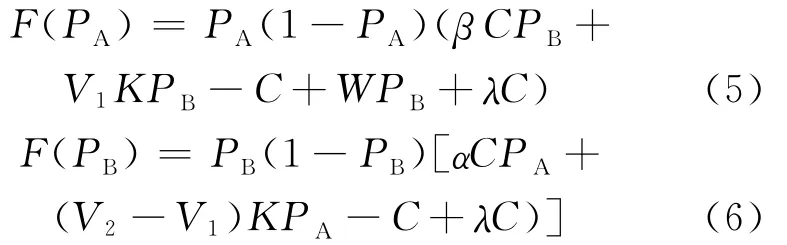
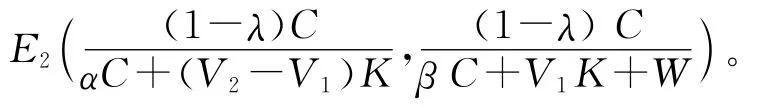
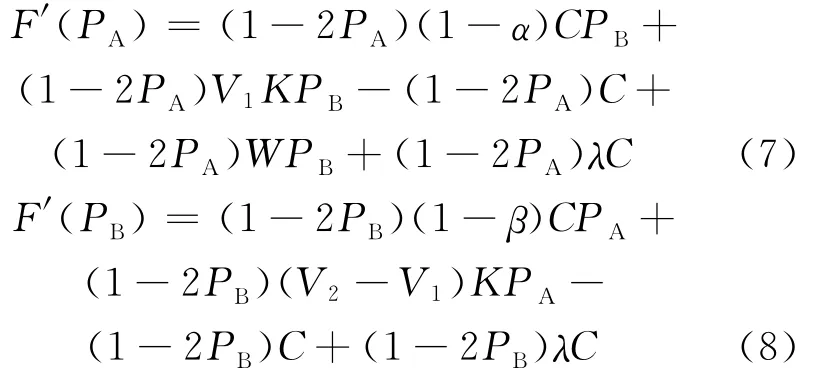
图4 惩罚机制下群体A的复制动态相位图

图5 惩罚机制下群体B的复制动态相位图

1.3 企业与监管方的行为策略演化博弈模型

根据企业与监管方的博弈支付矩阵，可以得到双方在不同策略下的适应度。企业采取共生策略的适应度为q（－C＋V）＋（1－q）（－C＋V），企业采取不共生策略的适应度为q（－λC－W）＋（1－q）（－W），故企业的平均适应度为p（－C＋V）＋（1－p）（－W－λqC）。

第三方监管机构采取共生策略的适应度为p（－f）＋（1－p）（λC－f），采取不共生策略的适应度为0，故监管机构的的平均适应度为qλC（1－p）－qf。根据复制动态方程定义，可得企业与监管机构的复制动态方程为：

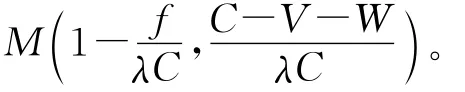
根据演化博弈理论，可知演化稳定策略需局部均衡点满足条件F′（x）＜0，由复制动态方程可得：

当q＜（C－V－W）／（λC）时，F′（p）｜p＝0＜0及F′（p）｜p＝1＞0，p＝0为演化稳定策略。当q＞（C－V－W）／（λC）时，F′（p）｜p＝0＞ 0及F′（p）｜p＝1＜0，p＝1为演化稳定策略。当q＝（C－V－W）／（λC）时，对所有的p恒有F′（p）＝0，此时企业中共生行为的可能性均为稳定状态。

当p＜（1－f／λC）时，F′（q）｜q＝0＜0 以及F′（q）｜q＝1＞0，q＝0 为演化稳定策略。当p＞（1－f／λC）时，F′（q）｜q＝0＞ 0 以及F′（q）｜q＝1＜0，q＝1为演化稳定策略。当p＝1－f／λC时，对所有的q恒有F′（q）＝0，这意味着第三方监管机构执行监督的可能性均为稳定状态。

2 模型分析

图6 博弈双方复制动态示意图

图6中CEB点构成的折线为企业选择收敛于不同策略的临界线，当初始状态在CDBE点构成的区域中时，策略选择收敛于企业间的共生关系策略，当初始状态在ABEC点构成的区域中时，策略选择收敛于点（0，0）。企业共生行为的演化过程是一个试错的过程，行为主体在这个过程中不断地调整修改策略，因此它是一个漫长的过程，可能在很长时间内，IES中的企业群体间保持共生策略选择与不共生策略选择并存的局势。

由图6可知，在企业群体A与企业群体B的演化博弈模型中，影响演化模型中初始状态的参数有：交易的副产品或废弃物的总量K；交易价格V1、V2；建立共生关系的成本C；副产品或废弃物的处理费用W；成本分摊系数α、β；考虑惩罚机制时的惩罚比例系数λ。

分别讨论这些参数如何影响企业群体A及企业群体B的策略选择，对其中某一影响因素进行讨论，是以其他参数值不改变为前提的。

（1）对于上游企业群体A，由鞍点E的横坐标可知，若成本分摊系数α越大，即企业群体A承担的成本占总成本的比例越大，水平方向上鞍点E越靠近点A，因此，当企业群体A的成本分摊比例越大时，企业群体A的策略选择收敛于共生的概率就越大。若V2－V1越大，即企业群体A与企业群体B的副产品的交易价格与企业群体B寻找的替代品价格差价越大，此时水平方向上鞍点E越靠近点A，当V1与V2价格差异越大时，企业群体B参与合作的积极性越强，增加了上游企业群体A对企业群体B的合作信任度，从而提高了企业群体A选择共生策略的概率。

（2）对于下游企业群体B，由鞍点E的纵坐标可知，若成本分摊系数β越大，即企业群体B承担的成本占总成本的比例越大，此时垂直方向上鞍点E越靠近点A，因此，当企业群体B的成本分摊比例越大时，企业群体B的策略选择越收敛于共生的概率就越大。若废弃物的交易价格V1越高，此时垂直方向上鞍点E越靠近点A，可知副产品或废弃物售出所带来的收益是下游企业选择共生的重要激励因素之一，在废弃物的交易价格严格低于替代品的条件下，废弃物的交易价格越高，作为上游企业群体A解除共生关系的可能性越低，增加了企业群体B对企业群体A的合作信任度，从而提高了企业群体B选择共生策略的概率。若废弃物的处理费用W越大时，由图6可知，鞍点E越靠近点A，点CDBE构成的区域面积越大，企业群体B的策略选择收敛于共生的概率就越大。因此，对参与产业生态系统的企业适当增加污染治理费用，将有利于企业群体之间建立产业共生关系。

（3）对于共生关系链上企业群体双方，若副产品或废弃物总量K越大，鞍点E越靠近点A，点CDBE构成的区域面积越大，因此，企业群体A的策略选择收敛于合作的概率就越大。当建立共生关系的投入成本C越小时，鞍点E越靠近点A，这表明企业之间建立共生关系所需技术、设备以及搜寻、谈判成本越小时，折线CEB上方的区域面积越大，企业策略收敛于合作点的概率就越大。因此，降低建立企业共生的投入成本将有利于提高产业共生行为的稳定性。

而投入成本的减少离不开政府的激励政策，企业的决策行为根据地方政府激励力度的大小而决定，同时其决策也反作用于政府的政策选择［12－13］，政府给予的资金及技术等方面的支持将促进企业趋向于采取共生策略。

（4）对于共生关系链上企业群体双方，当考虑惩罚机制时，比例系数λ越大，即监管机构提高对选择不共生企业的赔偿费用，此时鞍点E越靠近点A，因此，建立监管机构是阻碍机会主义行为的有效途径，从而提高产业生态系统中企业建立共生关系的稳定性。由企业与第三方监管机构的博弈模型可知，对于企业博弈方，若λ越小，水平方向上鞍点M越靠近点A，但是垂直方向上却越远离点A。结合企业群体间的博弈模型，可知惩罚系数λ越小，惩罚机制促进企业采取共生策略的效果越来越不明显，而监管博弈方也将会选择不监督策略。对于第三方监管博弈方，若λ越大，垂直方向上鞍点M越靠近点A，但是水平方向上鞍点M越远离点A，这表明当惩罚系数λ越大时，监管博弈方将会选择监督策略，而企业博弈方将会采取不共生策略，这就会违背建立第三方监管机构的意愿。