基于AUSM改进格式的超声速射流数值模拟

杨风波，马大为，乐贵高，聂 赟

（1.南京理工大学 机械工程学院，南京210094；2.北京机电工程总体设计部，北京100854）

超声速射流问题广泛存在于现代航空航天和火箭导弹发射等科学技术领域，而超声速伴随使得已经具有间断波系结构的超声速射流问题趋于复杂化。鉴于试验设备及试验费用昂贵，不能提供流场波系结构演化的具体过程，研究分辨率高、求解经济性好的数值格式，开展燃气射流的数值模拟工作，成为燃气射流研究领域的一种必要手段，也是试验研究的有效补充。

目前，在模拟超声速流动方面，稳定性好、间断分辨率高的格式主要有TVD、ENO、WENO、NND、有限元、紧致格式和矢通量分裂等［1－8］。文献［2，6，8］分别采用TVD格式、间断有限元格式和矢通量法对超声速喷流进行了数值模拟，捕捉的波系结构也越来越清晰，但均没有给出压力等值线，对接触间断没有给出具体解释。另外，上述格式求解过程多数伴随着特征矩阵的分裂和特征值的求解，过程繁琐、求解经济性差。上世纪90年代，Liou和Stefen综合矢通量分裂方法（FVS）［9］和通量差分分裂方法（FDS）［10］的优势，构造了著名的混合通量差分AUSM［11］（Advection Upstream Splitting Method）格式。为了有效抑制“红宝石”现象，消除间断附近的数值伪振荡和抹平现象，Liou后续推出了 AUSM＋［12］格式，Kim 提出了AUSMPW［13］和 AUSMPW＋［14］改 进格 式。AUSM系列格式将数值通量分解为对流项通量和压力项通量，对流通量包含了马赫数、当地声速，以及相应的流动特征通量，压力通量仅仅含有压力项；另外，该系列格式通量求解无需求解Jacobian矩阵，在计算效率方面具有很大优势。

以Liou提出的AUSM＋格式为基础，针对超声速伴随射流特殊波系结构及超声速区和低速区同时存在的问题，对该格式进行了适宜改进，构造了空间和时间均具有二阶精度的数值格式，并发展到二维轴对称Euler方程组进行数值求解。数值计算结果与试验纹影图吻合良好；该格式能清晰捕捉入射激波、反射激波、λ激波，接触间断等现象，并且基本无“红宝石”现象，表明该格式具有较强的激波和间断捕捉能力。

1 控制方程和离散方法

1.1 控制方程

在忽略化学反应、粘性和热传导的假设下，轴对称流动Euler方程组的守恒形式可以表述为

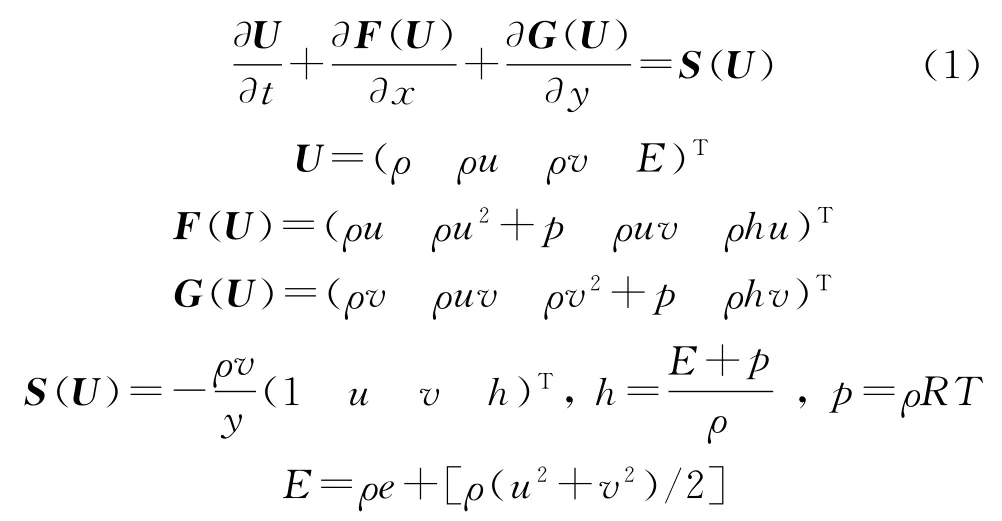
式中：t为时间变量；ρ为密度；u，v分别为x，y方向速度分量；p为压强；R为气体常数；T为气体温度；γ为比热比；e为单位质量内能；E为单位体积总能量；h为单位体积总焓。

1.2 空间离散

采用改进型的AUSM＋格式对控制方程（1）进行离散，得到如下轴对称Euler方程组的半离散有限差分方程：

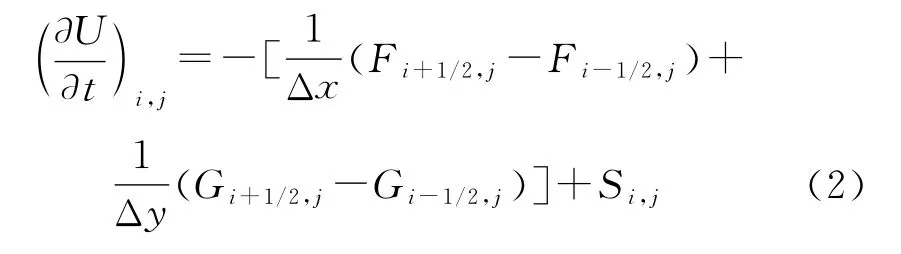
式中：Δx和Δy分别为轴向和径向坐标方向上的空间步长。

1.3 空间格式构造方法

以单元交界面Fi＋1／2，j无粘通量 为 例，改进 的AUSM＋格式数值通量的构造过程如下。

定义：

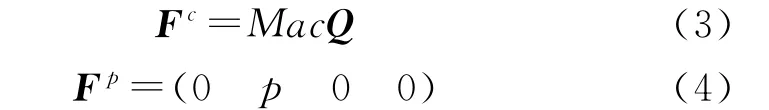
式中：Fc，Fp分别为对流通量项和压力通量项；c为当地声速；Q＝（ρρuρvρh）；Ma为马赫数。

将无粘通量Fi＋1／2，j分裂为对流通量项和压力通量项进行处理，即

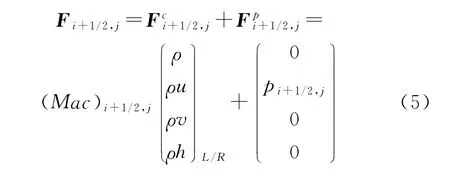
式中：定义Mai＋1／2＝ui＋1／2／ci＋1／2；L／R表示速度为正向，则取边界L通量（左通量），速度为反向，则取边界R通量（右通量）。

1.3.1 对流项通量

考虑到界面马赫数Mai＋1／2，j受左右特征波影响的物理特性，将边界马赫数作如下处理，即：

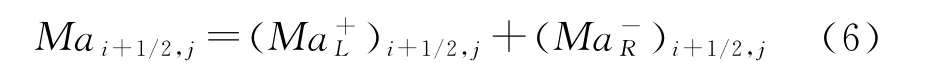
式中：＝Ma＋（MaL），＝Ma－（MaR）。

为了改进传统AUSM格式的不足，更好地反应特征波传递对流场的影响，消除激波后形成的“红宝石”现象，给出如下形式的马赫数分裂函数［15］：

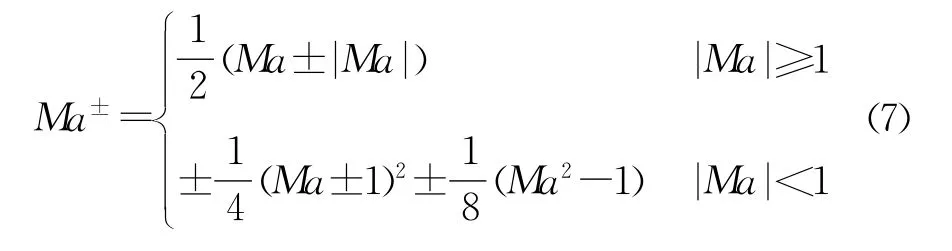
在低速流动区域，为加速收敛，且抑制数值振荡，对边界马赫数进行了修正［16］：

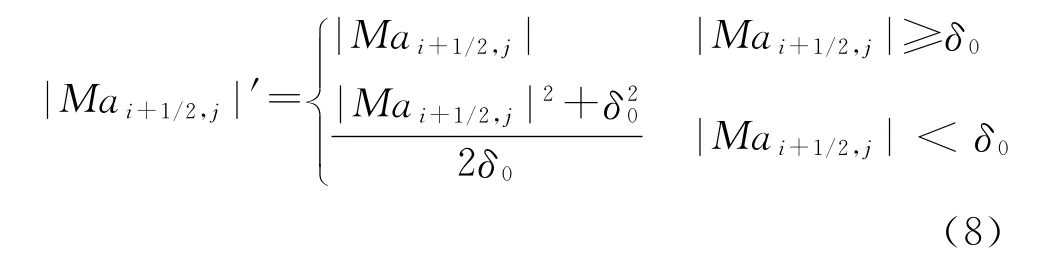
式中：δ0为小量，δ0＝δ1｜Ma∞｜，δ1∈［0.05，0.5］。

对流通量项可以表述为

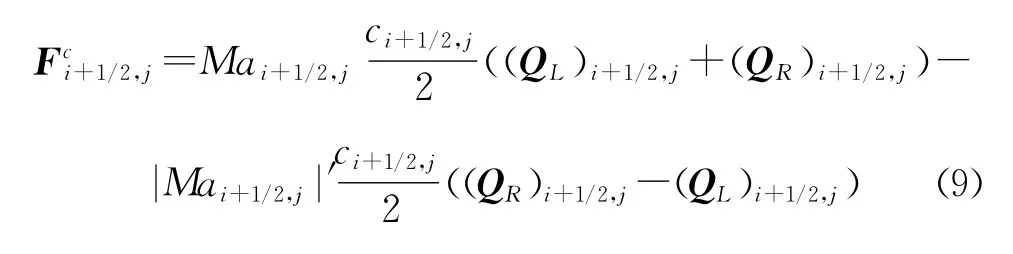
1.3.2 压力项通量

和对流通量类似，界面上引入压力分裂函数：

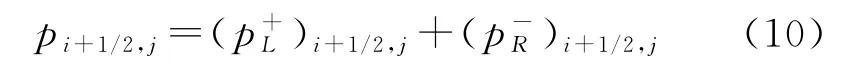
式中：

1.3.3 高阶格式构造

为将AUSM＋格式推广到高阶格式，且防止在激波附近出现过冲或过膨胀，捕捉更为清晰的波系结构，引进Van Leer可微保单调限制器，对界面两侧原始变量进行处理，以获得重构的无粘通量。

Van Leer可微保单调限制器［17］满足：

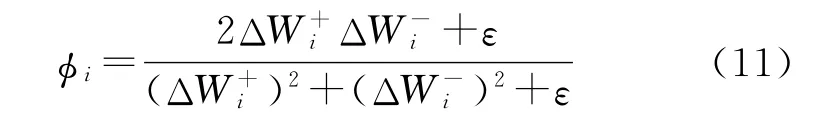
式中：ΔW＋i＝Wi＋1－Wi，ΔW－i＝Wi－Wi－1，W为原始变量（ρuvp）T；ε是一个防溢出的小量。

则可构造如下界面两侧原始变量的数值通量：

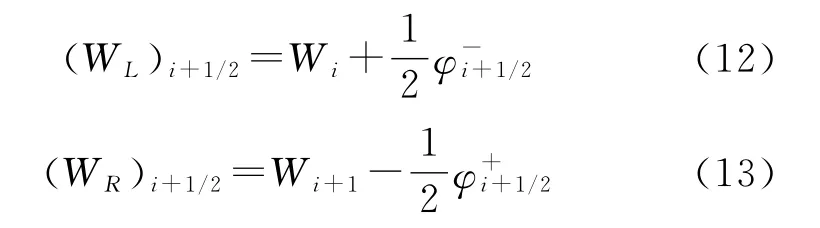
1.4 时间离散

为了与空间高精度匹配，时间离散采用二阶精度Runge－Kutta法。

将式（2）右边各项统一定义为Ri，j，则有：

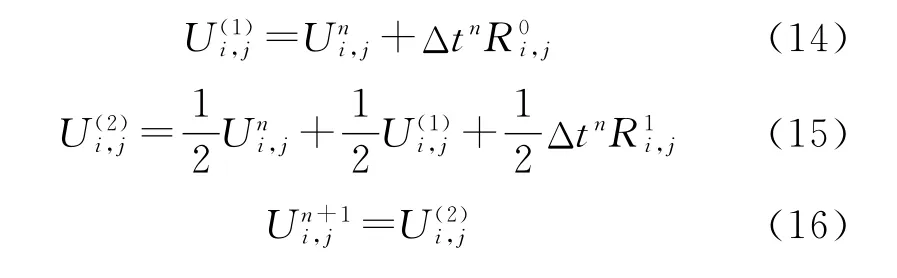
2 计算结果与分析

图1为发动机喷管喷流计算区域，表示通过射流中心轴线一半计算区域。取［0∶1.5］×［0∶3.5］（径向×纵向）的计算区域（将喷口外径无量纲化为1，且喷口外径长度用de表示，如图2～图4所示），采用144×60正方形网格对该区域进行离散。流动参数见表1，r和R分别为喷管出口的内、外径，下标j表示喷管出口的流动参数，下标∞表示超声速外流的流动参数。GH为入口边界，DE为超声速来流条件，EF和FG为镜面反射边界，CD为简单波边界，CB为外推边界，AB为轴对称边界，其它计算区域假定为超声速自由来流的初始条件。

图1 计算区域

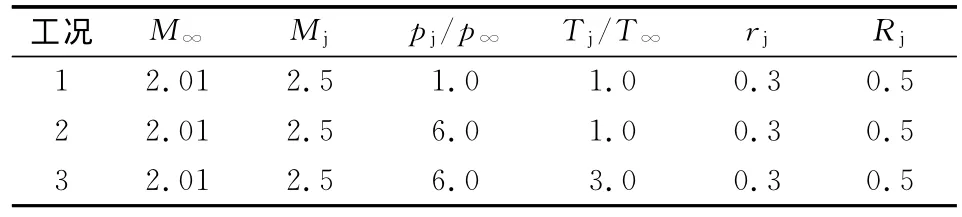
表1 流动参数

图2给出了工况1的密度等值线和马赫数等值线分布图及在相同流动条件下的试验纹影图。

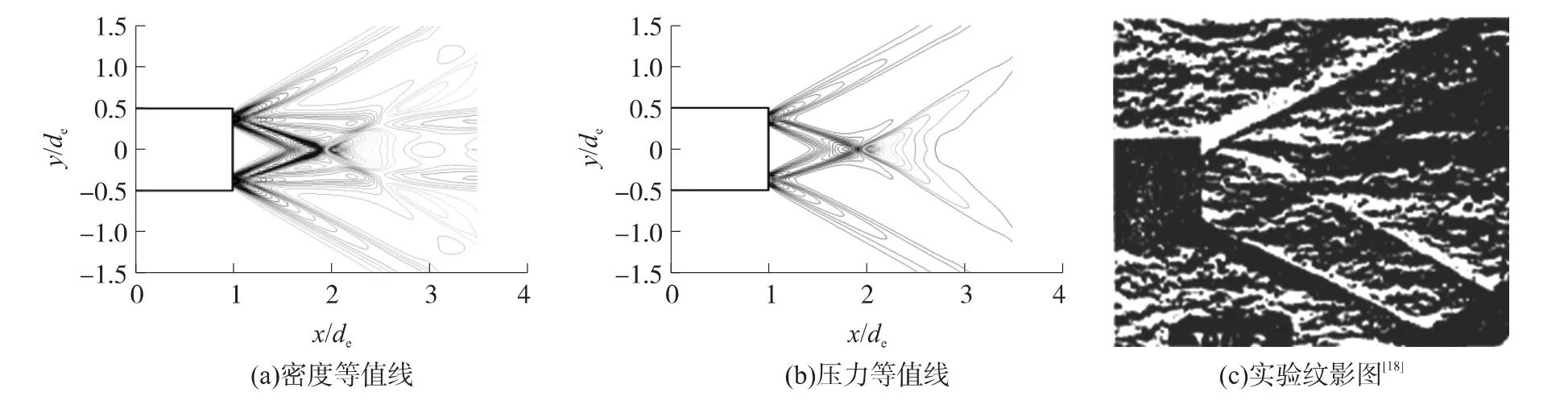
图2 算例1的等值线与纹影图

从图2可以看出，在超声速伴随射流中，没有出现燃气射流中常见的三波点等经典波系结构。超声速来流在喷管拐角处强烈压缩喷口射流，出现两道斜激波、射流激波。从密度等值线可以看出，第二道斜激波和第一道入射激波中间存在两道间断，从图2（b）中可看出，由于压力等值线中无间断产生，故该间断为接触间断。文献［2，6，8］均没有给出压力等值线，没有对接触间断进行判定。第一道斜激波后伴随有膨胀扇产生，第二道斜激波下方的射流激波受压缩遇到中心轴线发生反射，反射激波和接触间断相交，马赫盘结构消失，从以上分析可看出，超音速伴随使得已经具有间断的超音速射流波系结构更加复杂。另外，通过对比分析可以看出，流场结构与相同流动条件下三阶DG－FEM格式［6］的计算结果是一致，优于二阶TVD格式［2］，数值模拟的波系结构和流场特征和试验纹影图［18］吻合良好，表明二阶AUSM格式的数值模拟结果是可信的。

另外，为了说明本文网格布局与数值求解结果的合理性，采用三种网格布局对工况1进行求解与对比分析。计算结果如表2所示（轴线上的压力用pz表示），从表2可以看出，网格过稀对计算结果的精度影响较大，而网格达到一定密度时，计算结果与网格基本无关，从表2可以看出，网格3在网格2的基础上增加网格密度2／3，射流激波反射点的位置和反射点压力基本一致。故本文采用144×60的网格密度（径向×纵向）。

表2 工况1的三种网格布局对比

图3给出了工况2的密度、压力等值线图和对应的试验纹影图。由于压力比提高，射流中心区域明显更大，马赫盘位置向下游移动，出现了由一道斜激波和一道入射激波共同组成的λ激波，与相同流动条件下三阶DG－FEM格式［6］的计算结果是一致的。和工况1类似，在斜激波和入射激波中间出现了一道弧线状的接触间断。相对于工况1而言，工况2的反射激波张角更大，激波和接触间断均变成了一道，这些超声速伴随射流流动特征与相同流动条件下的试验纹影照片［18］反映的流场特征基本一致。从图3也可以看出，密度和压力等值线基本没出现“红宝石”现象，激波清晰且薄，说明本文改进合理，有较高分辨率。

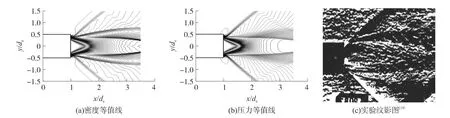
图3 算例2的等值线与纹影图

从图4可以看出，改进的AUSM＋格式捕捉到的流场波系结构很清晰，明显优于TVD格式［2］。和工况2相比，工况3中仍然能清晰看到入射激波和斜激波组成的λ激波，以及其间的接触间断。另外，对比工况2和工况3，可以看出，当保持喷管出口马赫数和出口压力不变而增大出口温度比时，出口斜激波张角几乎保持不变，但马赫盘的位置明显更靠近喷口，射流激波在中心轴线上的正规反射点距喷口平面的距离明显更小，这与文献［2］的分析是一致的。

图5给出了3个工况轴线上的压力pz分布规律。图中给出了改进的AUSM＋格式和二阶TVD格式计算对比值，从图中可以看出2种方法的计算结果吻合较好，但在间断附近存在差异。当喷流在膨胀区受超声速来流压缩，在中心轴线上发生正规反射后，反射点后的马赫数降低而压力迅速升高，压力呈现大梯度变化现象。在计算区域内，工况1和工况3中，改进的AUSM＋格式的压力计算值在反射间断点处迅速上升，表现为在间断点处具有较强的激波捕捉能力，而TVD格式在反射点捕捉到的梯度有抹平现象，捕捉间断能力稍差。

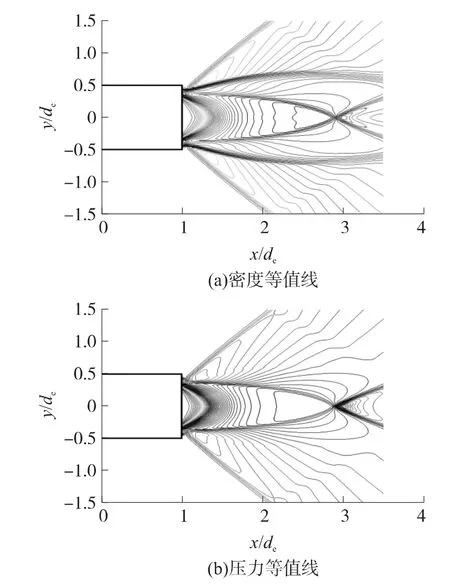
图4 算例3的等值线

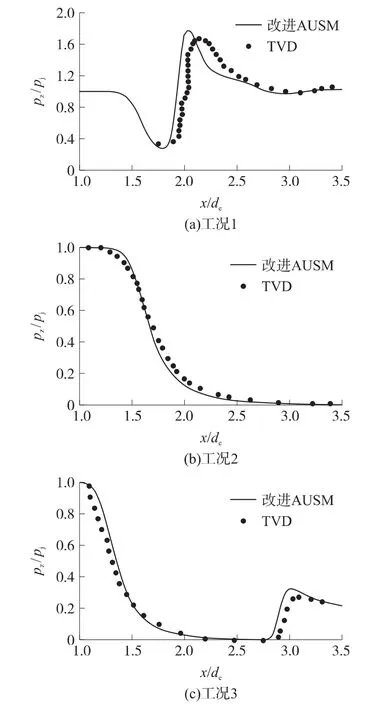
图5 轴向压力分布

文献［18］给出了和本文工况1和工况2同初始条件和结构参数下流场中喷管壁面的压力和远场压力的比值参数，为进一步验证改进的AUSM＋格式在超声速伴随射流中的计算精度，图6给出了工况1和工况2情况下超声速伴随流场中喷管壁面的压力pw分布曲线和在相同流动条件下测得的试验结果。pw／p∞为壁面局部压力和无穷远处静止大气压力之比，图6中黑色间断点为文献［18］中的试验结果。从图6（a）和图6（b）中可以看出，数值计算结果与相同条件下的试验结果吻合很好。

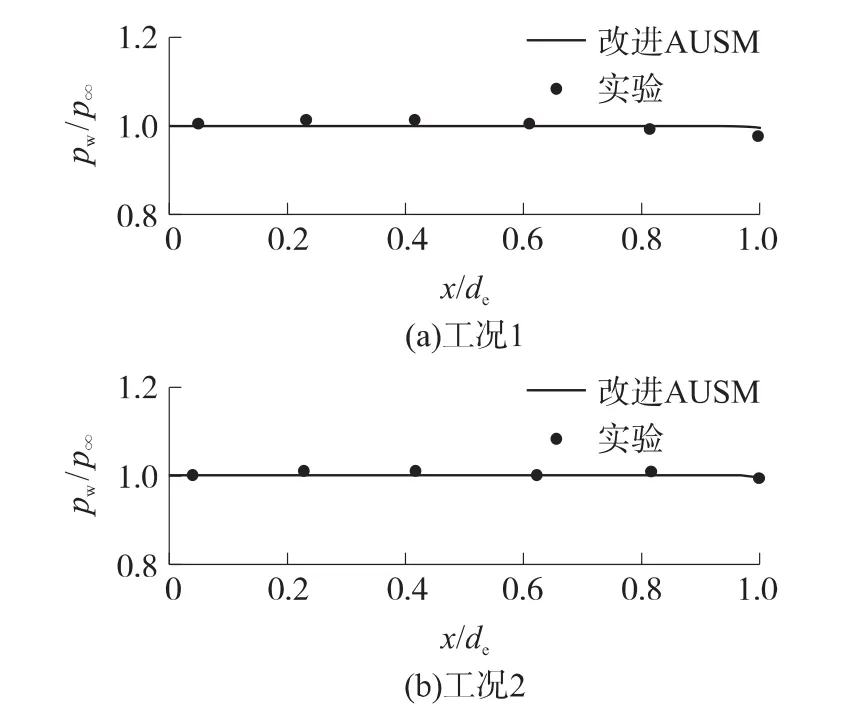
图6 喷管壁面压力分布

3 结束语

将改进的AUSM＋格式发展到轴对称Euler方程组进行数值求解，给出了无粘数值通量的详细构造，对3种超声速伴随射流进行了数值模拟，结果显示，喷流出口压力越大，马赫盘位置越靠近下游，出口斜激波张角和出口温度基本无关。

改进的AUSM＋格式能有效消除“红宝石”现象，捕捉到的波系结构清晰，较好地预测了接触间断等超声速伴随射流特有的波系结构。

对比已有二阶TVD格式，改进的AUSM＋格式对激波间断具有更强的捕捉能力，能较好抑制间断附近振荡、前冲、抹平等现象，能较好反应间断附近变量的大梯度变化现象。

轴对称工况的波系结构等值线图与相同工况下的已有文献结果、试验纹影照片吻合较好。

［1］徐旭，张振鹏.用TVD方法模拟喷管内的横流流场［J］.推进技术，1997，18（15）：53－57.XU Xu，ZHANG Zhen－peng.The numerical simulation of cross－flow in nozzle by using a TVD scheme［J］.Journal of Propulsion Technology，1997，18（15）：53－57.（in Chinese）

［2］乐贵高，马大为，臧国才.火箭底部流动的TVD数值模拟［J］.弹道学报，1995，7（1）：35－40.LE Gui－gao，MA Da－wei，ZANG Guo－cai.Numerical simulation of flow in rocket base by TVD［J］.Journal of Ballistics，1995，7（1）：35－40.（in Chinese）

［3］候中喜，易仕和，王承尧.超声速开式空腔流动的数值模拟［J］.推进技术，2001，22（5）：400－403.HOU Zhong－xi，YI Shi－he，WANG Cheng－yao.Numerical analysis of supersonic open cavity［J］.Journal of Propulsion Technology，2001，22（5）：400－403.（in Chinese）

［4］徐文灿，黄振宇.高精度ENO格式在射流数值模拟中的应用［J］.空气动力学学报，2001，19（4）：401－406.XU Wen－can，HUANG Zhen－yu.Calculations of jets flowfield with high resolutions ENO［J］.Acta Aerodynamica Sinica，2001，19（4）：401－406.（in Chinese）

［5］郑敏，张函信.无波动、无自由参数的耗散差分格式（NND）在喷流计算中的应用［J］.空气动力学学报，1989，7（3）：35－40.ZHENG Min，ZHANG Han－xin.Application of non－oscillatory and non－free－parameters disspative finit difference scheme to the calculation of free－jet flows［J］.Acta Aerodynamica Sinica，1989，7（3）：35－40.（in Chinese）

［6］陈二云，马大为，乐贵高，等.间断有限元方法在弹尾超音速喷流计算中的应用［J］.计算物理，2008，25（6）：705－710.CHEN Er－yun，MA Da－wei，LE Gui－gao，et al.Discontinuous finite element method for supersonic flow of a missile propulsive jet［J］.Chinese Journal of Computational Physics，2008，25（6）：705－710.（in Chinese）

［7］沈孟育，张志斌，牛晓玲.满足抑制波动原则的五阶精度紧致格式［J］.清华大学学报，2002，42（11）：79－82.SHEN Meng－yu，ZHANG Zhi－bin，NIU Xiao－ling.Fifth－order accurate compact scheme that suppresses oscillations［J］.J Tsinghua Univ，2002，42（11）：79－82.（in Chinese）

［8］聂赟，乐贵高，马大为.矢通量分裂法在喷管超声速喷流计算中的应用［J］.固体火箭技术，2013，36（1）：56－60.NIE Yun，LE Gui－gao，MA Da－wei.Application of flux vector splitting method to the calculation of supersonic flow on nozzle jet［J］.Journal of Solid Rocket Technology，2013，36（1）：56－60.（in Chinese）

［9］LIOU M S，STEFFEN C J.A new flux spliting［J］.Journal of Computational Physics，1993，107（1）：23－39.

［10］VAN L B.Flux－vector splitting for the euler equation［J］.Lecture Notes in Phys，1982，170：507－512.

［11］LIOU Meng－sing.A new flux splitting scheme［J］.Journal of Computational Physics，1993，107：23－39.

［12］LIOU M S.Progress towards an improved CFD methods：AUSM＋，AIAA95－1701－CP［R］.1995.

［13］KIM K H，RHO O H.An important of AUSM scheme by introducing the pressure－based weight functions［J］.Computers＆ Fluids，1998，27（3）：38－80.

［14］KIM K H，RHO O H.Methods for the accurate computations of hypersonics flows，I.AUSMPW＋scheme［J］.Journal of Computational Physics，2001，174：38－80.

［15］刘晨，王江峰，伍贻兆.预处理AUSM＋格式在全速域反应流模拟中的应用［J］.航空动力学报，2009，24（8）：1 831－1 836.LIU Chen，WANG Jiang－feng，WU Yi－zhao.Application of preconditioned AUSM＋scheme on numerical simulation of reacting flows at all speeds［J］.Journal of Aerospace Power，2009 24（8）：1 831－1 836.（in Chinese）

［16］梁德旺，王可.AUSM＋的改进［J］.空气动力学学报，2004，22（4）：404－409.LIANG De－wang，WANG Ke.Improvement of AUSM ＋scheme［J］.Acta Aerodynamica，2004，22（4）：404－409.（in Chinese）

［17］ANDERSON W K，THOMAS J L.VAN L B.Comparison of finite volume flux vector splitting for the Euler equations［J］.AIAA，1986，24：1 453－1 460.

［18］AGRELL J，WHITE R A.An experiment investigation of supersonic axisymmetric flow over boattails containing a centered propulsive jet，FFA－TN－AU－913［R］.1974.