人行索桁桥振动分析及舒适度评价

曹玉贵，胡 隽，李小青，庄劲松，冯万里

(1.华中科技大学土木工程与力学学院，湖北武汉430074;2.江苏省宿迁市泗阳县交通运输局，江苏宿迁223700)

伴随着我国基础设施建设的不断发展，人行桥建设发展迅速.大跨度、窄桥面的索桁桥由于造价低廉、施工方便，在我国交通不便的西部山区应用较多，但是作为行人通道的人行桥跨度大、结构复杂，大多存在人致振动问题.2000年英国千禧桥在开通当日即发生过度横向振动事件，并且发现其他桥上也有过同样的过度振动现象发生，引起了人们极大的重视［1-2］.我国也有一些人行桥振动导致行人不适的问题发生［3］，这不仅影响结构的安全和使用寿命，而且有可能影响人正常行走甚至引起恐慌.目前国内对人行桥舒适度的研究主要集中于简支梁桥或者连续梁桥，对人行索桁桥舒适度的研究尚未见报道.

索桥的舒适度主要体现在桥梁的加速度方面，吊杆的布置、桥面系的结构形式、桥梁本身的阻尼都会影响到索桥的振动.为增加桥梁刚度，国外主要是对管道悬索桥加设反向缆，或同时采用倾斜的吊杆，以增大全桥的刚度［4-5］.而索桁桥是由上缆、下缆通过锚旋和吊索张拉成拉索桁架，提高桥梁整体刚度.为此，本研究以某人行索桁桥为例，采用ISO 10137《结构设计基础—建筑和人行道抗振的适用标准》规定的人行荷载的力学模型对桥梁进行振动分析［6］，并对其舒适度进行评价.

1 分析模型

某人行索桁桥，由上、下缆索、吊杆及桥面系组成.人行道板立面线形向上拱起，主缆通过主塔塔顶，在锚碇处进行锚固，人行道桥面索锚固在主塔基础上，主索和桥面索通过锚碇和吊索张拉成拉索桁架，两片桁架通过桥面系连成一整体.这类人行索桁桥梁的主要构件包括:主缆、桥面索、主塔、人行道系统、主锚碇和主塔基础等.

与传统的柔性人行悬索桥的主要区别在于，人行索桁桥承重结构是由施加了预应力的主索、桥面索和吊索组成的索桁架结构，缆索系统在荷载作用下始终都保持拉应力，从而提高了柔性索桥的刚度.但是，由于恒载较小，桥面索矢度受到桥面线形限制等因素，索桁架仍属柔性索桥体系.其结构形式见图1.

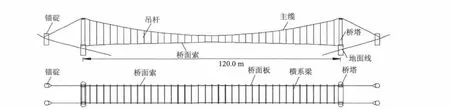
图1 索桁桥立面和平面构造图

人行索桁桥桥面宽2.1 m，主跨跨径为120.0 m，不设边跨.吊杆间距为2.0 m，跨中吊杆长取1.5 m，横梁采用槽钢，通过桥面索与桥面钢板焊接成整体，横梁间距2.0 m，全桥横梁总数等于吊杆根数.主索的矢跨比为1/10，主索是由2根直径为46 mm的钢绞线组成，其密度为7 850 kg·mm-3.桥面索上拱度取为3.0 m，取缆索材料弹性模量E=1.1×105MPa.截面形式如图2所示.

从受力体系看，索桁桥属于单跨柔性悬索结构，为了确保结构安全性和设计合理性，需要采用三维实体有限元法对其受力特性进行分析.在本桥有限元模型中，主索和桥面索在模型中采用link10单元，纵梁在模型中采用beam 4单元，桥塔采用变截面beam188单元.为了简化分析，桥面的钢桁架假设为相同的截面形式，因此，可以假定桥面板的荷载均匀分布在桥面上.桥面索搁在横梁上，并与横梁焊在一起.在模型中，设定横梁与桥面索共用节点.

图2 人行索桁桥横截面示意图

2 索桁桥振型分析

分析人行索桥的自振特性时，首先要解决的问题，是求解一个广义特征值的问题.由于在人行索桥的空间有限元模型中，虽然节点的自由度数目很多，但只需要了解相对较少的一些低阶频率和相应振型，就可以较好地研究其动力特性.因此，本研究采用子空间迭代法，求解人行索桥的自振频率和振型.

由于结构的自振特性与结构的质量和刚度有关，为了结果的准确性，Ansys可将模拟二期恒载和横隔板等效的荷载转换为质量［7］，建立模型如图3所示.在结构动力性能分析中，一般情况下结构前几阶自振频率和振型起控制作用，所以只需计算结构的前几阶自振频率和振型.在此对人行索桁桥采用分块兰索斯法进行模态分析.

图3 索桁桥有限元模型

索桁桥前30阶的自振频率见表1.图4-6分别为不同振动模态的第1阶振型.

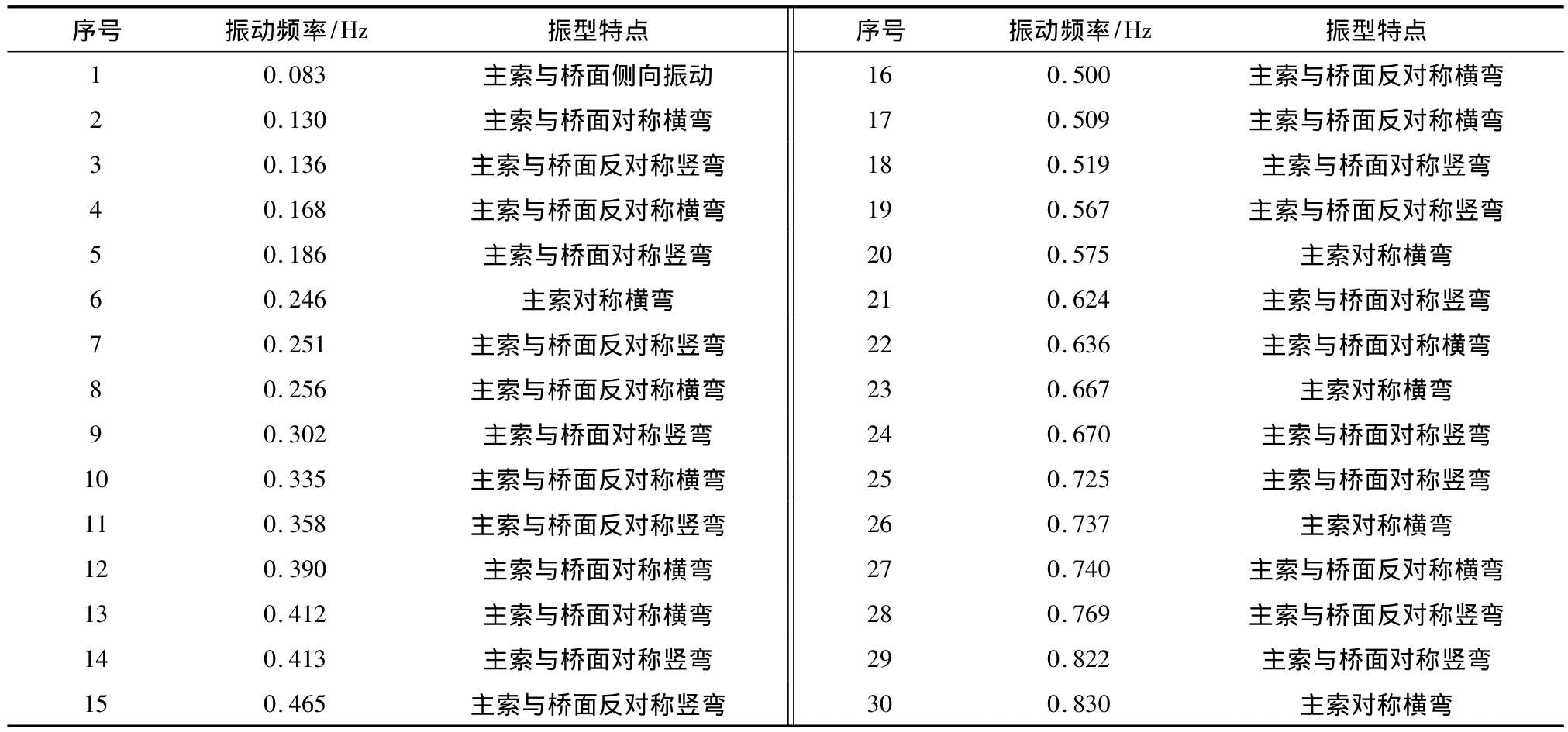
表1 索桁桥的自振特性

图4 第1阶振型(横向弯曲)

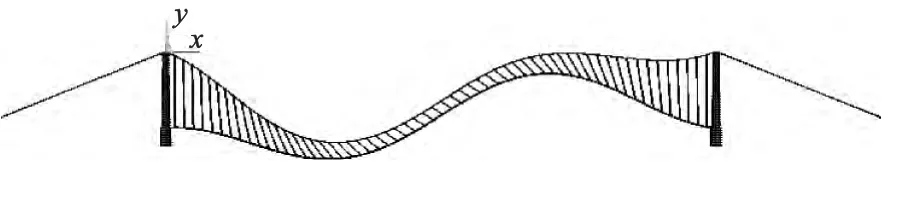
图5 第1阶振型(竖向弯曲)

图6 第1阶振型(反对称横弯)

值的注意的是，虽然悬索桥通常有横向、竖向、扭转和纵向移动等4种振动模态［8］，但表1结果表明，由于人行索桁桥的桥面索锚固在桥塔上，人行索桁桥没有纵漂振型.本桥的第1阶振型发生在面外，为1阶主索与桥面侧向振动;第2阶振型发生在面外，为主跨对称横弯;第3阶振型发生在面内，为1阶主跨反对称竖弯;第4阶振型为主索横弯.由于本桥跨径较大，结构柔性非常大.因此，振动频率也比较低，前30 阶自振频率分布在0.08 ～0.80 Hz，可认为该桥前30阶振型不会被人群荷载激起共振［9］.

传统的大跨悬索桥动力特性包括:基频都是1阶对称横向弯曲振动，且基本周期很长，如江阴大桥达到了 19.6 s，虎门大桥为 11 s［10］.由于跨度大，且为悬吊结构，以加劲梁振动为主的频率都很低.由表1可知:索桁桥的刚度较大，最大振动周期为12.1 s.由表1还可知:大跨索桁桥动力刚度增大，对提高其抗风性能很有利;且由于其刚度增大，对地震荷载的响应有可能会增大，这是不利的因素.通过对该桥的动力特性进行分析，计算所得该桥的基频为0.082 8 Hz，对应振型为主索与桥面侧向振动.根据BS 5400《英国人行桥规范》和EN 1990《欧洲结构设计规范》，当人行桥竖向基频小于 3.0 Hz，横向基频小于 1.5 Hz时，应该进行人致振动分析和评估.

3 人行桥振动荷载

桥梁的振动可以分为竖向振动和水平振动.目前对人行桥舒适度的研究主要集中于竖向舒适度.而Dieckmann的研究结果表明:人类对4 Hz以下水平方向振动的敏感性要大于竖向方向振动的敏感性［11］.

3.1 人行荷载的力学模型

ISO 10137针对人行桥振动舒适性，要求设计者分析人行桥结构在单个行人或人群激励下的加速度响应，将求出的加速度响应均方根值与规范中提供的振动舒适度曲线进行比较，以判定结构振动舒适性［6］.

1)单人荷载模式.

竖向周期性荷载模式为

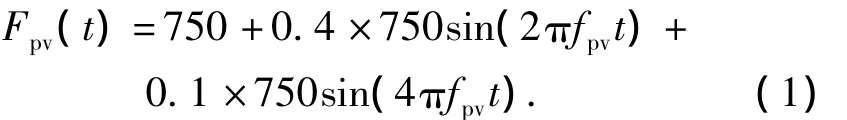
侧向周期性荷载模式为

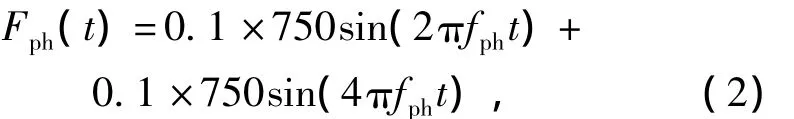
式中:fpv为行人竖向步频;fph为行人侧向步频.在求解人行桥在单个行人荷载激励下的响应时，行人荷载将作为集中荷载作用在容易引起最大响应的位置处.

2)人群的荷载模式.

ISO 10137对于人群荷载作出的相应规定，是以人群密度来考虑人群数量.人群数量N由下式可得:

式中:S为人群密度，S=0～1.5人·m-2;B为人行桥的宽度;L为人行桥的计算跨径.

当桥上人群以同步伐行走时(步频相同、步幅相同)，计算振动响应时采用式(3)的荷载形式，即将总人数与单个行人荷载乘积均摊到整个结构上，获得等效的均布周期性荷载.本研究采用1.0人·m-2的密度布置行人，使其匀速不断的通过桥梁.

人群荷载同步时，竖向周期性荷载模式为侧向周期性荷载模式为

当桥上人群以非一致性步伐行走时，行人引起的部分振动效应会相互抵消，因此，ISO 10137通过非一致调整系数C(N)来考虑步伐非一致性对振动响应的影响，调整系数为

人群荷载步伐不一致时，竖向周期性荷载模式为

侧向周期性荷载模式为

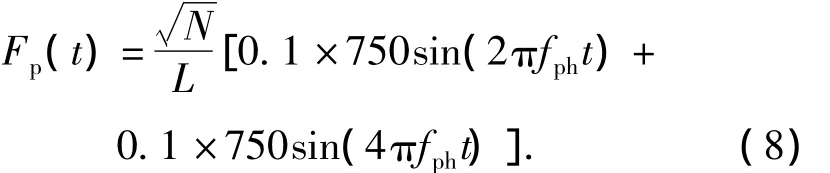
3.2 计算结果分析

人行激励振动的特性取决于人行荷载的特殊性，人的行走由连续的步子形成，具有周期性.这种周期性激励在竖向和侧向都可以用傅立叶级数的形式表示，级数中高阶频率是基频的整数倍，但基频大小在竖向和侧向不同.竖向振动由人行走时重心的上下起伏对桥面产生的垂直方向上的动力荷载引起，行人正常行走步频介于1.6 Hz(慢走)和2.4 Hz(快走)之间，平均值大约是2.0 Hz，且标准差较小.因此，人行竖向激励的傅立叶级数的基频大约是2.0 Hz［11］.

本研究基频取2.0 Hz.侧向振动由人行走时重心从一脚移到另一脚时，身体呈侧向Z字形移动产生的周期性激励力引起.当左脚站立迈出右脚时，这个力的方向指向左边，反之，指向右边.在左右脚各跨出一步后，完成一个循环(即2个单步).所以，基频总是竖向荷载频率的1/2，大约为1.0 Hz.本研究基频取 1.0 Hz.

采用Ansys有限元分析软件的瞬态分析，通过命令流给指定节点施加人行荷载.为了模拟真实的行人行走，本研究根据行人步幅，对节点施加人行荷载.根据上面的人群理论知识，节点上施加的荷载为单个行人荷载的2倍.模拟多人同时行走，整个时间由行人通过天桥的行走时间确定.表2给出Ansys计算人行索桁桥各节点的响应结果.

表2 人行索桁桥的最大加速度 m·s-2

以上分析得到的结构竖向与侧向加速度响应时程可以看出，人行索桁桥的加速度较小.单人行走时，横向和竖向加速度在桥梁跨中处达到峰值.在人行荷载激励作用下，结构侧向振动加速度峰值与竖向振动加速度峰值的出现在时间上存在一定延迟，侧向振动加速度峰值稍晚，这说明结构竖向振动在一定程度上引起结构侧向振动.

4 舒适度分析

相关规范对人行桥竖向振动舒适度指标的规定较多［12］.因为人行桥与一般结构的振动有明显不同，可能在行走激励作用下同时产生竖向及侧向振动，即出现双向耦合振动，如果按现行评价标准，仅单纯考虑某一方向的振动舒适度显然不够合理.采用总乘坐值，考虑同时具有竖向和侧向振动的情况［13］，计算公式如下:

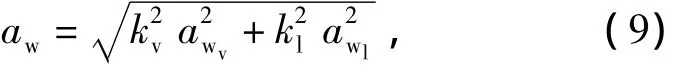
式中，awv，awl以及kv，kl分别为结构竖向及侧向振动加速度与振动迭加乘子.若将侧向振动等效为等舒适度的竖向振动，则kv=1，kl取值与结构竖向和侧向振动在其基准频率上的加速度界限有关，按照EN 1990《欧洲结构设计规范》的规定，可取kl=5.因此，式(9)可表示为

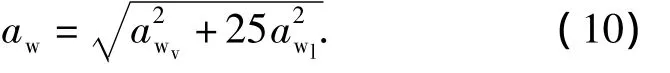
利用等效后的竖向振动加速度值可对人行桥的振动程度做出综合评价.标准建议了总乘坐值与人体振动舒适度的对应关系.表3为总乘坐标值与主观感受的关系.

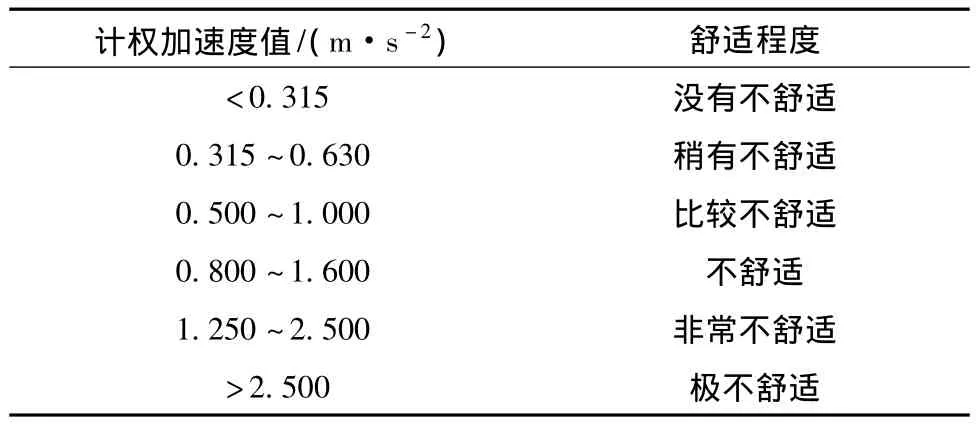
表3 总乘坐标值与主观感受的关系

综合考虑各种评价指标，参考表3可知，该人行桥在竖向和侧向的最大加速度分别为0.254 630 m·s-2和0.015 980 m·s-2，处于没有不舒适状态.计权加速度最大值为0.266 900 m·s-2，处于没有不舒适状态，因此，不会发生由于行人共振效应所引起的超越舒适度指标的振动.

5 结论

1)通过对人行索桁桥自振频率进行分析，得出相应的振动频率，确定了人行索桁桥不会被人群荷载激起共振.

2)采用ISO 10137标准构建的行人荷载模型，对人行索桁桥进行了人致振动分析和舒适度分析.结果表明:该结构形式的人行索桁桥的舒适度能够满足舒适度要求.

3)与其他普通悬索桥相比，由主索、桥面索和吊索组成的新型索桁桥，能够在满足使用要求、舒适度要求的同时，减轻了桥梁的质量，降低了经济成本.

References)

［1］Dallard P，Fitzpartrick T，Low A，et al.London Millen-nium Bridge:pedestrian-induced lateral vibration［J］.Journal of Bridge Engineering，2001(6):412-416.

［2］Nakamura S，Kawasaki T.Lateral vibration of footbridges by synchronous walking［J］.Journal of Constructional Steel Research，2006，62(11):1148-1160.

［3］Ingólfsson E T，Georgakis C T，Jönsson J.Pedestrian-induced lateral vibrations of footbridge:a literature review［J］.Engineering Structures，2012，45:21-52.

［4］Huang M H，Thambiratnam D P，Perera N J.Dynamic performance of slender suspension footbridges under eccentric walking dynamic loads［J］.Journal of Sound and Vibration，2007，303(1-2):239-254.

［5］Faridani H M，Barghian M.Improvement of dynamic performances of suspension footbridges by modi-fying the hanger systems［J］.Engineering Structures，2012，34:52-68.

［6］InternationalOrganization for Standardization. ISO 10137:2007 Bases for Design of Structures-Serviceability of Buildings and Walkways Against Vibration［S］，2007.

［7］罗如登.Ansys中砼单元Solid65的裂缝间剪力传递系数取值［J］.江苏大学学报:自然科学版，2008，29(2):169-172.Luo Rudeng.Values of shear transfer coefficients of concrete element Solid65 in Ansys［J］.Journal of Jiangsu University:Natural Science Edition，2008，29(2):169-172.(in Chinese)

［8］Huang M H，Thambiratnam D P，Perera N J.Vibration characteristics of shallow suspension bridge with pretensioned cables［J］.Engineering Structures，2005，27(8):1220-1233.

［9］钱 骥，孙利民.大跨径人行桥人致振动舒适性评估及减振措施［J］.上海交通大学学报，2011，45(5):677-681.Qian Ji，Sun Limin.Comfort evaluation and vibration reduction design of long span footbridges［J］.Journal of Shanghai Jiaotong University，2011，45(5):677-681.(in Chinese)

［10］赵长军.大跨索桁桥初步设计研究［D］.杭州:浙江大学建筑工程学院，2002.

［11］陈政清，华旭刚.人行桥的振动与动力设计［M］.北京:人民交通出版社，2009:74-98.

［12］Nakamura S，Kawasaki T，Katsuura H，et al.Experimental studies on lateral forces induced by pedestrians［J］.Journal of Constructional Steel Research，2008，64:247-252.

［13］法永生，李 东，孙翠华.人行桥随机人行荷载下的振动分析及其舒适度评价的新方法［J］.振动与冲击，2008，27(1):119-123.Fa Yongsheng，Li Dong，Sun Cuihua.Vibration analysis for a footbridge under stochastic pedestrian load and a new method for comfort evaluation［J］.Journal of Vibration and Shock，2008，27(1):119-123.(in Chinese)