凸轮泵内部瞬态流场的动网格数值解析
2014-12-23黎义斌李仁年孟庆武
黎义斌,李仁年,贾 琨,孟庆武,毕 祯
(1.兰州理工大学能源与动力工程学院,甘肃兰州730050;2.兰州理工大学机电工程学院,甘肃兰州730050;3.济南优科精流机械有限公司,山东济南250021)
凸轮泵属于非接触式转子泵范畴.目前已经在农产品加工、高黏性多相介质混输、固体悬浮介质传输等领域广泛应用.凸轮泵转子腔内装有2个相同的转子,转子间、转子与转子腔内壁间根据所输送的流质不同,设有一定的间隙.随着2转子的同步转动,流体通过泵入口被吸入转子腔,并在转子腔内获得一定的能量,在泵出口处,以一定的压力和速度排出.与离心泵和螺杆泵相比,凸轮泵适合泵送高黏度、高含固率和高杂质流体,并且泵送方向可以互换,其流量与流体黏度、输出压力无关;而离心泵流量随着流体黏度、输出压力增大迅速降低,并且黏度值、压力值达到一定值时,流量为0.
凸轮泵具有高效节能,特别是输送黏度较大的介质具有很大的优势.近年来,对于凸轮泵型线的研究有突破性的进展.S.Y.Jung等[1]在原有的型线(渐开线-椭圆)基础下,提出了多复合的转子型线(椭圆-渐开线-椭圆),有效地消除泵本身结构而引起的延迟现象.Yan Jia等[2]应用偏差函数(DF)方法对渐开线转子型线进行修正,从而达到高密封、高效率的效果.张铁柱等[3]提出了就摆线转子型线建立以小型轻量为目标的型线优化设计模型和内泄模型.目前,普遍采用CFD技术来研究泵内的流动特性[4-9],张锴等[10]利用动网格技术,对微型齿轮泵内部流场进行了非定常数值模拟.国内外研究主要集中在型线理论和优化算法方面,没有涉及到凸轮泵内部流场的数值研究.目前,采用CFD动网格技术能够动态实现凸轮泵内部流场的可视化,从而定量分析凸轮泵型线几何参数与流动参数的映射关系.
笔者以2叶型渐开线型线的凸轮泵作为研究对象,采用RNGk-ε湍流模型和动网格技术,对凸轮泵内部流场进行数值模拟,分析压力角对凸轮泵内部流场瞬态特性的影响.
1 转子型线数学模型
1.1 型线方程
凸轮泵的核心是一对共轭且形状相同的转子.对于凸轮泵转子的理论型线,除了满足共轭条件,应提高转子啮合过程中的强度和刚度,改善转子内腔体的容积利用系数,保证转子叶形有良好的几何对称性、互换性.目前常用的转子型线方程有渐开线型和摆线型,转子型线设计常用的设计方法有直角坐标法、极坐标法等.文中针对渐开线转子建立描述转子轮廓的型线方程.
渐开线凸轮泵转子型线如图1所示,在渐开线上任意取一点Z(x,y),θ角随Z点在渐开线BCE上的移动而变化.则Z(x,y)点的坐标方程为
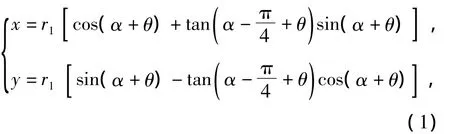
根据三角形关系可得

式中:r1为基圆半径;R为节圆半径;α为压力角.
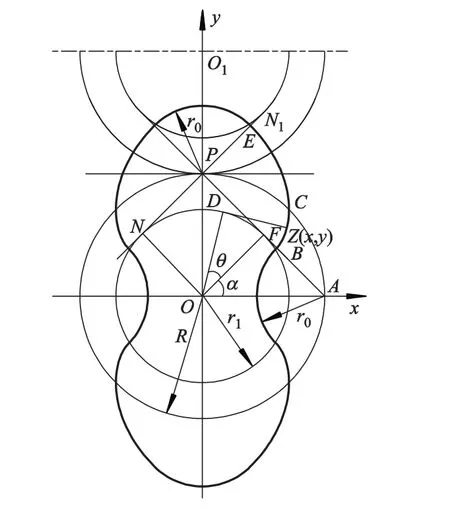
图1 渐开线凸轮泵转子型线
由渐开线啮合特性,当啮合点由E移动至P点时,节圆上的C点必然移动至P点,即节圆转动了1/8周期,齿顶圆弧和齿根圆弧半径r0为
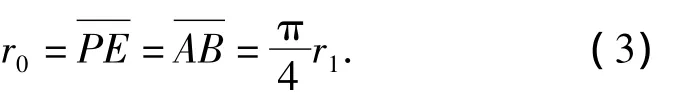
由此可见,齿顶圆弧和齿根圆弧半径r0与压力角α无关,而与基圆半径r1的大小有关.
为了使转子啮合时不产生干涉问题,应使转子啮合点位置不大于公法线与基圆的切点,即≤,计算可得 α≥38°8'46″,所以,渐开线转子型线方程的压力角α取值在40°~50°之间.
1.2 设计参数和设计方案
凸轮泵属于回转式容积泵,主要由泵体、转子、泵盖、密封装置、齿轮传动装置和驱动装置等组成.其中凸轮泵额定参数:设计排量为6.9 L·h-1,额定压力为 101.325 kPa,转速为 300 r·min-1,效率为54%.泵体内具有一对凸轮转子同步反向啮合转动,转子之间的啮合状态是决定凸轮泵是否达到额定压力和设计排量的关键因素.理论上,在同步啮合转动过程中任意某一瞬时,2转子理论廓线存在唯一接触点.为保证泵的正常运转,防止凸轮泵转子间相互干涉引起摩擦和磨损,根据所泵送的流体介质不同,在2转子之间、转子与转子腔内壁间都设定某一间隙值,其中径向间隙为0.4 mm,忽略轴向间隙的影响.
2叶型凸轮泵三维模型如图2所示,凸轮泵过流部件主要由吸入端、主动转子、从动转子、凸轮泵腔体和排出端等组成.其中转子采用2叶型渐开线型线方程,吸入端和排出端直径均为40 mm.

图2 2叶型凸轮泵三维模型
当压力角介于40°~50°时,转子型线方程和基圆半径都会随之变化.为了阐明压力角对凸轮泵转子型线方程和几何参数的影响因素,选定不同压力角建立凸轮泵转子型线几何模型.模型参数如表1所示.

表1 转子几何参数方案
2 数值求解算法
2.1 动网格计算方法
在FLUENT中,动网格模型可以模拟由于流域边界运动引起流域形状随时间变化的流动状况.对于凸轮泵2叶型转子啮合的反向旋转运动,下一个时间步的运动是由当前时间步的计算结果确定,各时间步的体网格的变形基于边界条件新的位置,软件自动实现.所以动网格计算模型表示为
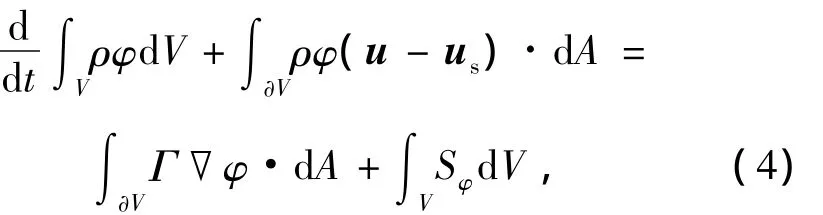
式中:ρ为液体的密度;u为液体的速度矢量;us为动网格的网格变形速度;A为面积;Γ为扩散系数;Sφ为通量的源项;∂V为控制体V的边界.
方程(4)中第1项可以用1阶向后差分形式表示为

式中n和n+1分别为当前和下一时间步的数值.
第(n+1)步的体积Vn+1为

对于渐开线凸轮泵转子型线及其网格区域,动网格更新方法采用局部网格重构,即将网格质量差的单元(单元尺寸太大或太小的单元,或者高度变形的单元)形成整体网格聚团区域,然后对网格聚团区域进行重构.对于整体选用块结构化六面体网格,把凸轮泵分成3部分:进口端、排出端和泵腔.结构网格模型及其拓扑结构如图3所示,通过网格无关性和时间步长独立性验证,当进口端、排出端网格为32.196万,泵腔网格数量为371.108万时,计算结果趋于稳定,与网格数和时间步长无关.其中凸轮转子之间的径向间隙处网格采用O型网格,径向最小间隙处网格为20层布局,可以精确计算径向间隙流场的细微特征,保证数值计算的准确性.

图3 结构网格模型及其拓扑结构
变形区域网格重构如图4所示,与运动分界线邻近的网格单元层为第j层,依据第j层高度h确定分裂形成新的单元层,或者与邻近的第i层合并形成新层.假定第j层单元面处于膨胀状态,FLUENT允许膨胀的高度为h=(1+αk)hideal,式中:hideal为理想单元面高度;αk为高度系数.当h>(1+αk)hideal时,单元将根据预定义的高度条件进行分裂,此时在第i层中的单元面高度是理想高度hideal.相反地,如果第j层中的单元体积处于压缩状态,当压缩到h<αkhideal时,被压缩的单元面将与邻近层的单元面合并成一个新的单元层.

图4 变形区域网格重构
2.2 UDF 处理方法
根据凸轮泵的运输介质做出假设:流体是恒温的牛顿流体,具有不可压缩性,流体初始状态是静止的.基于上述假设,采用RNGk-ε湍流模型,由于凸轮泵中的2个转子是随时间变化而进行同步转动,在计算中采用的是动网格,动网格可以模拟由流域边界运动引起流域形状随时间变化的流动,适合此模型计算.
FLUENT中,应用动网格模型计算并导入使2个转子反向同步旋转的UDF文件,程序如下:

2.3 湍流模型与边界条件
在CAD中建立不同压力角的凸轮泵计算模型,并导入网格划分软件ICEM CFD 14.5,整个凸轮泵的模型采用非结构网格和结构网格组成的混合网格.由于凸轮泵结构的局限性,工程中凸轮泵与单向阀配合使用.采用RNGk-ε湍流模型与隐式求解器,求解器控制采用PISO的压力-速度耦合模式,离散格式为二阶迎风格式,时间步长设为10-4s.固壁面设为无滑移壁面,即壁面上各速度分量均为0.对近壁面的湍流流动按标准壁面函数法处理.为了使模拟更接近实际运行条件,分别设置凸轮泵的输入端和输出端为压力进、出口条件,进口初始压力设定为0.103 MPa,并保持出口压力不变.监测进口和出口面的瞬时压力及瞬时流量,当入口面瞬时压力和出口面瞬时流量呈周期性波动时即认为计算收敛.
3 结果与分析
在凸轮泵内部流场模拟过程中,迭代初始时入口端和出口端监测点的参数脉动较为明显,当迭代1 500步后,各监测位置的参数变化趋于稳定.
t=0.25,0.30 s时,压力角 α =40°条件下凸轮泵内部流场的流线分布规律如图5所示,在凸轮泵转子域出口附近产生二次流动现象,凸轮泵内部的二次流动现象使局部流场产生流动分离和漩涡流,使凸轮泵的效率降低.

图5 不同时刻下流线分布
凸轮泵转子间采用非接触式的间隙配合,间隙随时间周期变化.排出端流量脉动规律如图6所示.

图6 排出端流量脉动规律
出口流量脉动周期与啮合转子的转速有关,随着凸轮泵压力角逐渐增大,凸轮泵排出口平均流量脉动值逐渐变小,压力角为40°时,凸轮泵的排出流量值最大.当凸轮泵压力角变化时,凸轮泵出口平均流量脉动的周期保持不变,表明压力角不是影响输出流量脉动的主要因素.
t=0.25,0.30 s时凸轮泵转子内部流场的速度等值线分布规律如图7-9所示.在同一时刻下,由于压力角不同而引起的不同模型产生的速度分布也不相同,介质入口湍流动能较小,湍流集中在间隙和出口处,随着压力角的增大,模型中最大湍流动能值逐渐变小的趋势.但相同的是模型中的最大速度会出现在转子的边缘处.在凸轮泵的工作过程中也会产生一定的负速度,也称为回流现象.
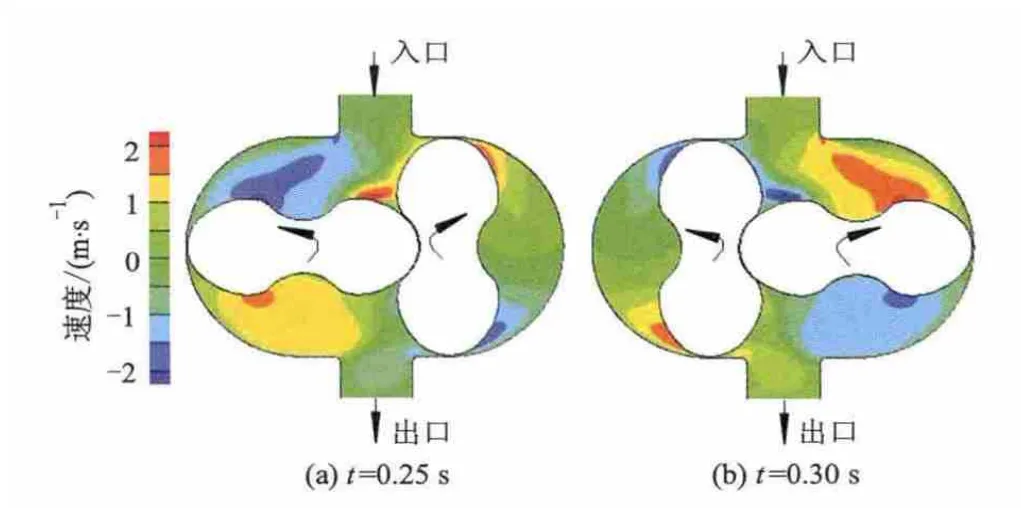
图7 方案1的速度等值线分布

图8 方案2的速度等值线分布
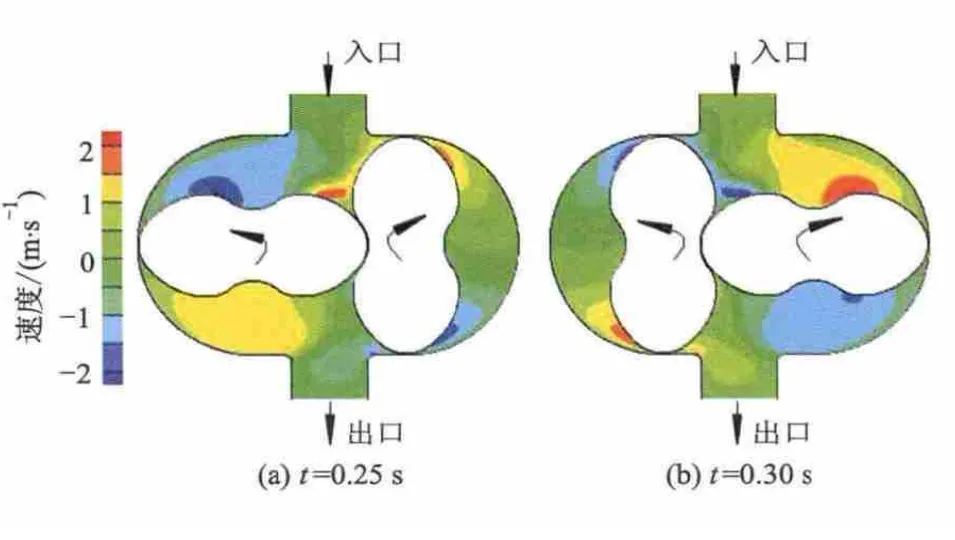
图9 方案3的速度等值线分布
在凸轮泵工作过程中产生的噪音主要源于机组周期性的压力脉动,如图10所示.对吸入端压力监测结果表明:压力角对吸入压力具有较大影响.随着压力角逐渐增大,吸入端压力波动的平均值逐渐变小,伴随着压力脉动幅值的减弱.因此,当压力角为40°时,吸入端压力值最大,压力脉动较为剧烈,转子压力角对吸入端压力值和压力脉动有显著的影响.结合图6及图10的分析表明:压力角一般介于40°~50°,当压力角为45°时,凸轮泵水力性能较好.
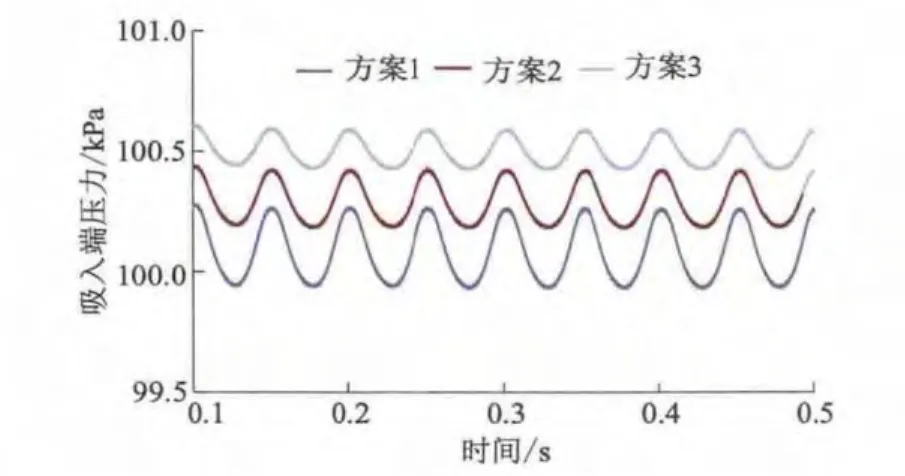
图10 吸入端压力脉动规律
瞬时条件下速度矢量分布如图11所示.
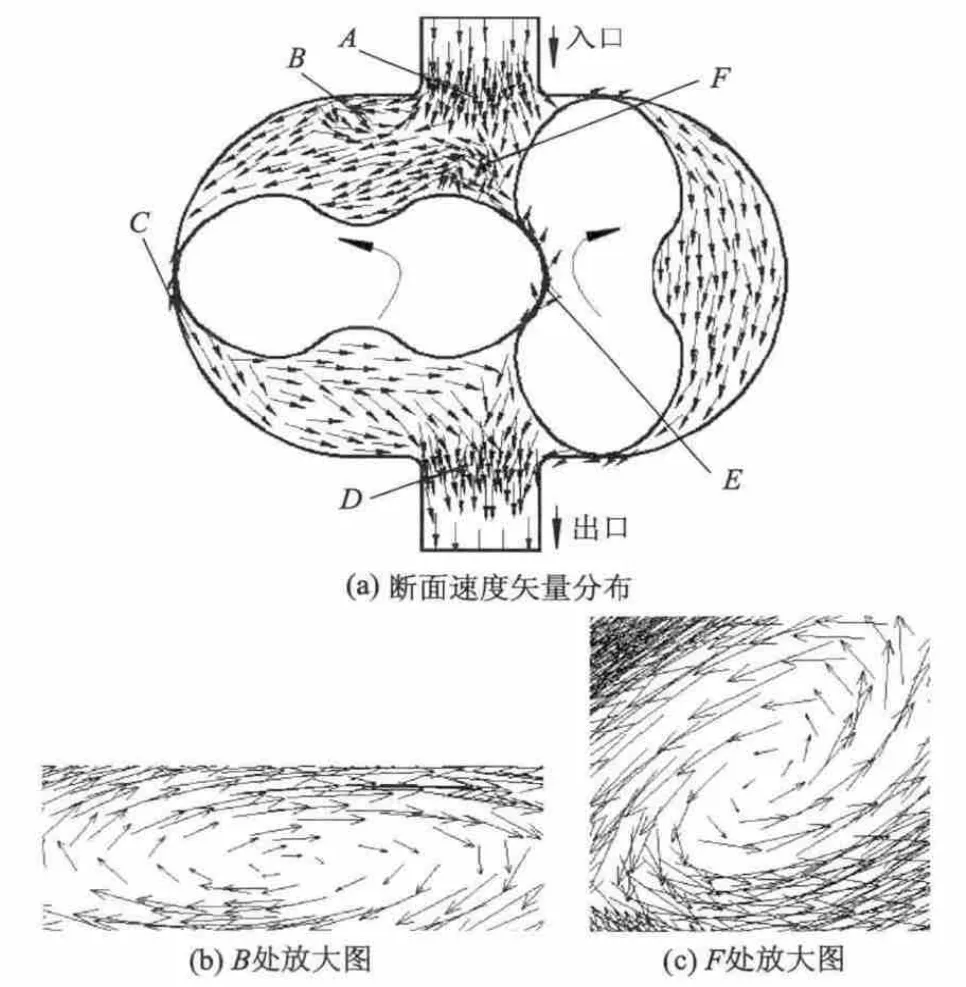
图11 瞬时条件下速度矢量分布
在主动轴的旋转驱动下,2转子作同步反向运动,液体进入转子腔的A处与排出转子腔时的D处时,由于转子腔内部计算边界的突扩和突缩效应,A处和D处存在较为明显的速度变化梯度和速度脉动.当液体从吸入端进入泵腔时,由于啮合转子之间的旋转效应,转子腔内部的容积发生周期性变化,特别在吸入端的B处和F处,容易诱发二次流和不稳定的漩涡,涡核内部的能量耗散使转子腔内部产生较大的局部水力摩擦损失.为了避免在两转子间以及转子与转子腔内壁间产生较大的水力损失,在凸轮泵转子和转子腔型线设计时,均给定一定的间隙值,图11中C处和E处,存在转子与转子腔内壁间隙以及2转子间隙,此间隙位置均存在一定的内漏,引起转子腔内液体的水力损失,一定程度上会影响凸轮泵的效率.压力角为45°时,不同时刻时凸轮泵内部流场的瞬时湍动能分布如图12所示.对比表明:凸轮泵吸入口处流场的速度分布较为均匀;随着两啮合转子同步反向旋转,液体获得了压力能的同时,由于转子高压腔的容积随时间呈周期性变化,所以排出口处流场的湍动能分布表现为周期性的瞬态效应.
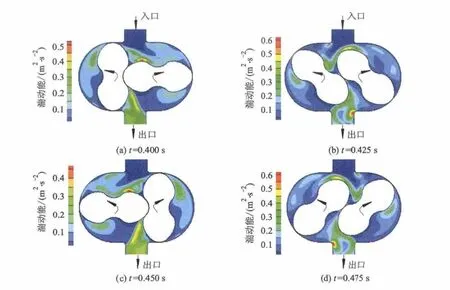
图12 瞬时条件下湍动能分布
为了分析转速对排出流量脉动的影响,分别选取转速为300,420,540 r·min-1得到转速与排出端流量脉动的关系如图13所示,随着转速逐渐增大,转子旋转周期降低,排液频率加快,因此排出口的流量脉动频率随之增加.当转速从300 r·min-1增加到420 r·min-1时,排出口平均流量值明显增加;当转速从420 r·min-1增加到540 r·min-1时,排出口平均流量值变化较小,但排出口流量脉动的幅值增加较为明显.

图13 转速与排出端流量脉动的关系
考虑到凸轮泵的结构特性,转子旋转一周时,排出端出现4次排液过程,这是造成排出口流量波动的主要原因.转速增加时,泵腔内部局部真空度较大,使吸入和排出的流量较大,这是造成排出口流量脉动的波峰和波谷相位变化的主要原因.
转速与排出端压力脉动关系如图14所示,转速的变化对排出压力和压力脉动产生较大影响.转速在300 r·min-1时,排出压力较小,液体排出过程产生的压力脉动也较小.研究表明:随着凸轮泵转速的增大,排出压力逐渐增大时,排出压力脉动的幅值逐渐增大,但转速提升到一定程度时,排出压力提高的幅度有限.

图14 转速与排出端压力脉动关系
4 结论
1)随着压力角逐渐增加,排出平均流量值与吸入平均压力值逐渐减小,但压力角与排出流量和吸入压力脉动周期无关.但在入口引起的压力脉动有增强的趋势.压力角为45°时,凸轮泵运行的水力性能最佳.
2)在不同转速工况下,随着转速的增大,排出流量和吸入压力均有明显的提高,瞬态过程的脉动现象逐渐明显.当转速增加到一定程度后,排出速度及吸入压力提高的程度有限,此时瞬态过程的脉动现象较为明显.
3)在凸轮泵工作过程中,由于转子之间、转子与泵体内壁之间、转子和泵盖内壁之间存在一定的间隙,导致漩涡的存在,使转子腔内能量损失增加,凸轮泵工作效率降低.
References)
[1]Jung S Y,Bae J H,Kim M S,et al.Development of a new gerotor for oil pumps with multiple profiles[J].International Journal of Precision Engineering and Manufacturing,2011,12(5):835-841.
[2]Yan Jia,Yang D C H,Tong S H.A new gerotor design method with switch angle assignability[J].Journal of Mechanical Design Transactions of the ASME,2009,131:011006-1-011006-8.
[3]张铁柱,张洪信,赵 红.非接触式转子泵理论型线与实际型线设计[J].机械工程学报,2002,38(11):152-155.Zhang Tiezhu,Zhang Hongxin,Zhao Hong.Design of theoretical and actual rotor curve of un-contact pump[J].Chinese Journal of Mechanical Engineering,2002,38(11):152-155.(in Chinese)
[4]朱荣生,胡自强,杨爱玲.双叶片泵内非定常流动的数值模拟[J].排灌机械工程学报,2011,29(1):26-30.Zhu Rongsheng,Hu Ziqiang,Yang Ailing.Numerical simulation of unsteady flow in double-blade pump[J].Journal of Drainage and Irrigation Machinery Engineering,2011,29(1):26-30.(in Chinese)
[5]孔繁余,薛 玲,王 婷,等.复杂泵体压力脉动特性的数值模拟[J].华中科技大学学报:自然科学版,2012,40(8):12-16.Kong Fanyu,Xue Ling,Wang Ting,et al.Numerical simulation of pressure fluctuation in complex pumps[J].Journal of Huazhong University of Science and Technology:Natural Science Edition,2012,40(8):12-16.(in Chinese)
[6]王 洋,王维军,刘 洋,等.多级潜水电泵非定常流动数值模拟及性能预测[J].江苏大学学报:自然科学版,2013,34(5):519-523.Wang Yang,Wang Weijun,Liu Yang,et al.Numerical simulation and performance prediction of unsteady flow in multi-stage submersible centrifugal pump[J].Journal of Jiangsu University:Natural Science Edition,2013,34(5):519-523.(in Chinese)
[7]王秀礼,袁寿其,朱荣生,等.离心泵汽蚀非稳定流动特性数值模拟[J].农业机械学报,2012,43(3):67-72.Wang Xiuli,Yuan Shouqi,Zhu Rongsheng,et al.Numerical simulation on cavitation unsteady characteristics in centrifugal pump[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(3):67-72.(in Chinese)
[8]施卫东,姚 捷,张德胜,等.采样频率和时间对轴流泵压力脉动特性的影响[J].排灌机械工程学报,2013,31(3):190-194.Shi Weidong,Yao Jie,Zhang Desheng,et al.Influence of sampling frequency and time on pressure fluctuation characteristics of axial-flow pump[J].Journal of Drainage and Irrigation Machinery Engineering,2013,31(3):190-194.(in Chinese)
[9]Zhang Desheng,Shi Weidong,Chen Bin,et al.Unsteady flow analysis and experimental investigation of axial-flow pump[J].Journal of Hydrodynamics,2010,22(1):35-43.
[10]张 锴,翟俊霞,陈嘉南,等.微型齿轮泵内流场的动网格模拟和分析[J].兰州理工大学学报,2011,37(1):45-49.Zhang Kai,Zhai Junxia,Chen Jianan,et al.Simulation and analysis of flow field inside micro-gear pump with dynamic mesh[J].Journal of Lanzhou University of Technology,2011,37(1):45-49.(in Chinese)
