同步多重工作休假排队系统分析
2014-12-23苑春荟朱翼隽
苑春荟,徐 剑,朱翼隽
(1.北京邮电大学经济管理学院,北京100876;2.江苏大学理学院,江苏镇江212013)
在过去的几十年里,国内外学者对经典M/M/1排队系统进行了广泛深入地研究,得到了许多有价值的科研成果[1-4],而这些科研成果也被应用于诸多领域,比如:计算机系统、通信网路系统和生产制造系统等.近年来,L.D.Servi等又引入了一种半休假策略:在休假期间服务台并不是完全停止服务而是以较低的服务率对顾客进行服务,这种半休假策略叫作工作休假(working vacation,WV)[5-7].如果工作休假的服务率退化为0,那么模型就归结为经典的休假排队.但是,在特定的排队系统中,例如:通讯网络中的数据传输,由于外来干扰信号的到达会抵消一部分传输数据,而这种外来干扰信号可以看作负顾客,带有负顾客的排队系统除了应用于通信系统外,还可以应用于生产制造系统或销售系统(这时负顾客可以看成是操作员的操作或是其他致使顾客离开的原因),并且顾客到达可能使服务员休假或者故障,负顾客的排队理论由此得到推广[8-10].结合实际应用情况,笔者提出另一种策略:休假可中止.例如:销售系统中,休假期间突然遇到顾客高峰[11].基于现实生活中通讯网络等各种排队系统的复杂性,提出负顾客、带休假可中止的同步多重工作休假排队模型.
1 模型描述
模型描述如下:
1)该系统是具有正负两类顾客的M/M/1排队,正负顾客均为泊松到达,到达率分别为λ和ξ.
2)到达的负顾客带RCE(removal customer at the end)抵消策略,即到达的负顾客一对一抵消队尾的正顾客(若有,不管正顾客是在等待还是在被服务),而若负顾客到达时系统中没有正顾客,负顾客就自动消失,负顾客本身并不接受服务.
3)当系统变为空时,服务台开始一个随机长度为V的工作休假,休假时间V服从参数为θ的指数分布,在工作休假期,服务员以较低的速率对正顾客进行服务.
4)服务台对正顾客在正规忙期和工作休假期的服务时间分别服从参数为μ1和μ2的负指数分布,这里 μ1> μ2.
5)有2种可能的方式从工作休假转入正规忙期:①工作休假期间完成1个顾客服务,并且系统中有顾客等待,则中止正在进行的工作休假转入正规忙期,若服务完成时,系统中无顾客,则继续保持在工作休假状态上;② 若某次工作休假结束时,系统内有顾客在场,正在进行的服务由速率μ2转换到速率μ1,开始1个正规忙期.若1次工作休假结束时,系统中无顾客,则服务台开始另1次独立同分布的工作休假.
6)假定:正负顾客的到达间隔,工作休假时间,正规忙期和工作休假期的服务时间相互独立,此外,服务规则为先到先服务(FIFO).
Qv(t)表示t时刻系统中的顾客数,J(t)的定义如下:

这样,{Qv(t),J(t)}是1个拟生灭过程(QBD过程),状态空间为 Ω ={0,1}∪{(k,j):k≥1,j=0,1}.过程的状态转移机制如图1所示.

图1 状态转移机制
如果将状态按字典序排列,其生成元可写成下列分块三对角形式:

其中:A0=-λ;C0=(0,λ);B1=(μ1+ ξ,μ2+ ξ)T;C=λI,I为二阶单位矩阵;
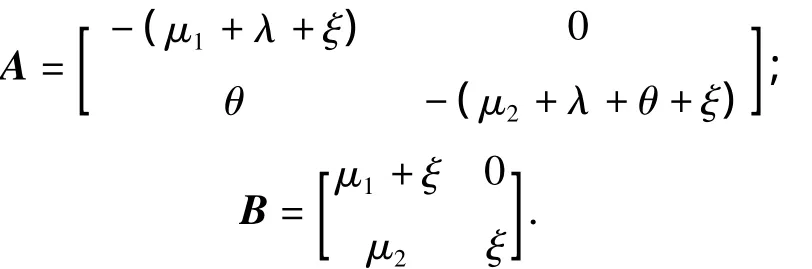
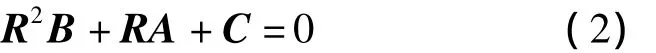
的最小非负解,这个解称为率阵,记为R.R在矩阵几何解中起着关键的作用.先假设
定理1 当ρ<1时,方程(2)有最小非负解:

证明 因为A,B,C都是下三角阵,也设R是

为了得到方程R2B+RA+C=0的最小非负解,在式(4)第1个方程中取r11=ρ,而另一根r11=1,由 式(4)中 第 2个 方 程 给 出r22=,另一根大于1,易证0<r22<1.
将r11,r22代入式(4)中的第3个方程可得
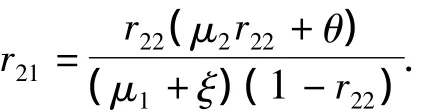
推论1r11,r22满足下列关系式:
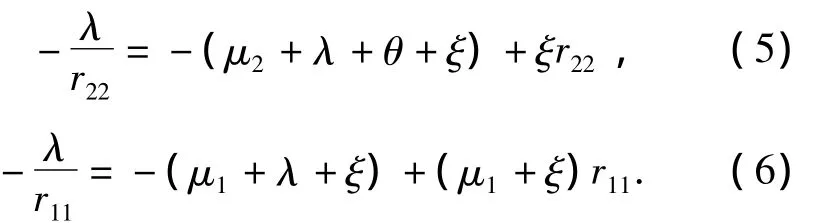
定理2 拟生灭过程{Qv(t),J(t)}正常返,当且仅当
证明 由率阵R的定义可知:SP(R)<1.当且仅当ρ<1,由文献[12]中定理2.4可证明过程正常返,当且仅当ρ<1.
2 队长的稳态分布
当ρ<1时,拟生灭过程{Qv(t),J(t)}是正常返的,(Qv,J)表示它的极限分布,将(Qv,J)的分布写成如下的分段形式 π =(π0,π1,π2,…),其中π0=(π01);πk=(πk0,πk1),k≥1,且
定理3 当ρ<1时,{Qv(t),J(t)}的稳态极限(Qv,J)的分布为
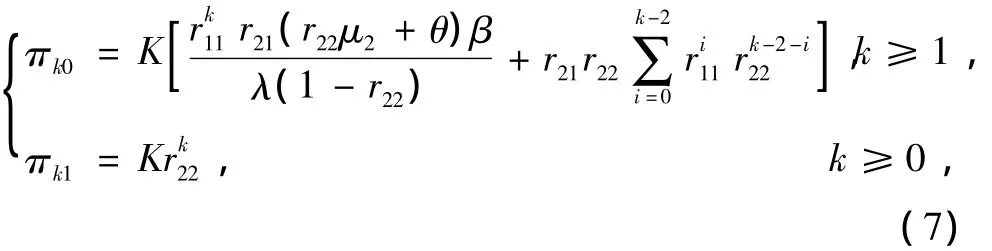
式中:r21,r22的取值同式(3);K为常数因子,

证明 下面先求B[R]及正左不变向量(π01,π10,π11),有

所以,由(π01,π10,π11)B[R]=0,可得方程组:
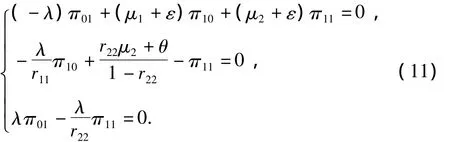
取 π01=K, 则 (π01,π10,π11)=K(1,,应用 M.Neuts[13]的矩阵几何解法,可得


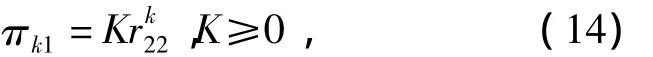
最后由正规化条件可求得常数因子K,即式(8).
3 稳态队长的条件随机分解

证明 由定理3可知,Q的概率母函数为

推论2 系统的平均附加队长:
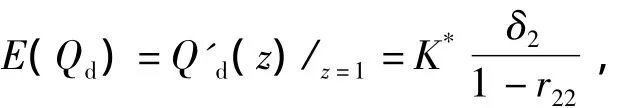
进一步得到系统的平均等待队长:

4 数值例子
通过以上分析获得了系统平均附加队长、平均队长等稳态指标.但作为管理决策者不仅要知道排队系统的稳态指标,还要了解系统中的某些参数对这些稳态指标的影响,从而使排队系统尽可能达到最优.稳态平均队长E(Q)和负顾客到达率ξ之间的关系如图 2 所示,当 λ =0.3,μ1=0.9,μ2=0.7时,不论休假率如何变化,平均队长也是随着负顾客到达率的增加而逐渐递减的.
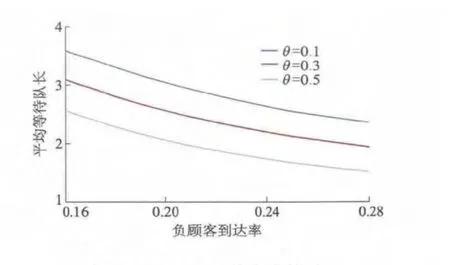
图2 E(Q)随ξ的变化趋势
5 结论
各种休假策略的研究为排队系统的优化设计和控制提供了更大的灵活性.考虑了一类带有负顾客、休假可中止的同步多重工作休假排队模型,通过计算、分析,给出了系统队长的稳态分布及系统队长随机分解结果.可将此模型应用到通讯网络系统中,当数据传送到服务台时,数据传送可看成正负顾客的到达,外来的干扰信号可看成负顾客的到达.考虑到在现实生活中,通讯网络的复杂性,服务台可能随时需要从工作休假转入正规忙期,于是提出了另一种策略:休假可中止.最后通过对数值的分析,更加清楚地了解了负顾客的到达对系统的影响.该模型在现代通讯网络中有很好的应用价值.
References)
[1]田乃硕.休假随机服务系统[M].北京大学出版社,2001.
[2]Krishna Kumar B,Arivudainambi D.Transient solution of anM/M/1 queue with catastrophes[J].Computers and Mathematics with Applications,2000,40(10):1233-1240.
[3]Di Crescenzo A,Giorno V,Nobile A G.On theM/M/1 queue with catastrophes and its continuous approximation[J].Queueing Systems,2003,43:329-347.
[4]Miller D R.Computation of steady-state probability forM/M/1 priority queues [J].Operations Research,1981,29(5):945-948.
[5]Servi L D,Finn S G.M/M/1 queues with working vacations(M/M/1/WV)[J].Performance Evaluation,2002,50:41-52.
[6]杨顺利,田乃硕.N-策略工作休假M/M/1排队[J].运筹与管理,2007,16(4):50-55.Yang Shunli,Tian Naishuo.TheM/M/1 queue with working vacations andN-policy[J].Operations Research and Management Science,2007,16(4):50-55.(in Chinese)
[7]Liu Wenyuan,Xu Xiuli,Tian Naishuo.Stochastic decompositions in theM/M/1 queue with working vacations[J].Operations Research Letters,2007,35(5):595-600.
[8]朱翼隽,顾庆凤.带RCE抵消策略的负顾客GI/M/1工作休假排队[J].江苏大学学报:自然科学版,2008,29(4):360-364.Zhu Yijun,Gu Qingfeng.GI/M/1 queue with RCE strategy of negative customers and working vacations[J].Journal of Jiangsu University:Natural Science Edition,2008,29(4):360-364.(in Chinese)
[9]Harrison P G,Pitel E.TheM/G/1 queue with negative customers[J].Advances of Applied Probability,1996,28(2):540-560.
[10]朱翼隽,刘海燕,王逢佳.带启动时间、N策略和负顾客的M/M/1工作休假排队[J].江苏大学学报:自然科学版,2012,33(5):616-620.Zhu Yijun,Liu Haiyan,Wang Fengjia.M/M/1 queue of working vacation with set-up timeN-policy and negative customers[J].Journal of Jiangsu University:Natural Science Edition,2012,33(5):616-620.(in Chinese)
[11]Li Jihong,Tian Naishuo.The discrete-timeGI/Geo/1 queue with working vacations and vacation Interruption[J].Applied Mathematics and Computation,2007,185(1):1-10.
[12]田乃硕,岳德权.拟生灭过程与矩阵几何解[M].北京:科学出版社,2002.
[13]Neuts M.Matrix-Geometric Solutions in Stochastic Models[M].Baltimore:The Johns Hopkins University Press,1981.
