基于点集与互信息的肺部CT图像三维弹性配准算法

夏 威，高 欣，王 雷，周志勇，张 冉

(1.中国科学院长春光学精密机械与物理研究所，吉林长春130000;2.中国科学院苏州生物医学工程技术研究所医学影像室，江苏苏州215163;3.中国科学院大学，北京100049)

肺部组织运动是复杂、不均匀的，为了获得肺部组织及病灶运动轨迹，文中借助影像信息，通过图像配准的方法，构筑肺部三维运动模型.图像配准是指确定两幅图像中对应点的位置关系，待配准的图像可以是不同时间点采集的图像或者属于不同模态的图像.弹性配准是医学图像配准的重要研究领域，常用于追踪病灶变化情况、运动校正、计算机辅助影像导航［1-3］.对一个周期内多个时间点上的肺部图像进行配准是术前计算机手术路径规划、模拟手术和手术导航的必要步骤.通过配准能够确定肺部组织的运动轨迹，提高手术器械在肺内部的定位.

目前主要有3种弹性配准算法:①基于特征的配准算法;②基于灰度的配准算法;③ 混合配准算法.基于特征的配准算法使用图像中明显的几何结构或者解剖特征做图像配准，例如特征点等，常用的特征点方法有SIFT点，SURF点等，医学图像中的特征点常由医生手动提取或者使用半自动的特征点标定系统.基于特征点的方法计算效率高，但是特征点的自动提取与精确匹配是一个难点［4］;另外，由于特征点分布稀疏，远离特征点的区域的变形场精度不高［5］.基于灰度信息的配准算法利用图像的灰度信息构成相似性测度来衡量配准的程度［3，6］，这种方法能够实现全自动配准，并且精度较高，但是会耗费更多的时间与内存.对于复杂的肺部图像配准，混合配准算法受到越来越多的关注，混合配准算法整合了基于灰度和基于特征的方法［7-8］，首先使用手动或者半自动的特征点提取方法提取气管或血管树的分支点，将分支点的位移信息作为灰度信息的约束，再使用基于灰度的配准算法进行配准，这种方法能够显著提高配准的精度，但特征点提取复杂费时不适用于临床［8］.

表面组织是肺部的显著解剖结构，表面分割的自动算法快速简单［9］.肺表面的膨胀与收缩反映了肺部组织的形变趋势，因此文中拟利用肺表面信息，提出一种全自动混合配准算法.该方法整合了基于特征与基于灰度的配准算法，先使用一致点漂移算法(coherent point drift，CPD)［10］得到点集位移向量，将点集位移向量与基于B样条变形模型［11］的位移向量之间的欧几里得距离最小化，得到基于B样条变形模型的大尺度变换函数，再将此大尺度变换函数作为基于互信息的配准算法［6］的初始变换函数进行细化配准.变换函数的计算中引入节点位移约束［11］，从而保证图像不会发生折叠现象，确保配准成功.

1 变形模型

给定一组肺部三维CT图像F和R，设F为浮动图像，R为参考图像，定义x=(x，y，z)为图像中体素的坐标.配准就是确定一个能使F匹配到R的变换函数T(x).

对于肺部复杂的弹性形变，需要先确立弹性变形模型，文中使用基于B样条的变形模型［11］.定义u为间距s=(sx，sy，sz)的均匀网格;di，j，k为网格u中第i，j，k个节点的位移.坐标x的变换函数定义如下［11］:

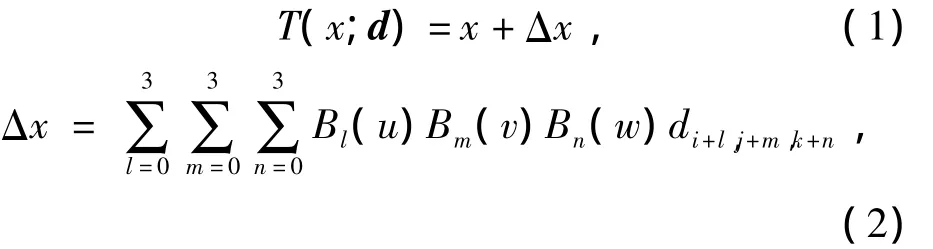
式中:i=⎿x/sx」-1，j=⎿y/sy」-1，k=⎿z/sz」-1，u=x/s-i-1，v=y/s-i-1，w=z/s-i-1;B0，B1，B2，B3是4个三次B样条基函数，即B0(t)=(-t3+3t2-3t+1)/6，B1(t)=(3t3-6t2+4)/6，B2(t)=(-3t3+3t2+3t+1)/6，B3(t)=t3/6，其中 0≤t＜1.

使用B样条变形模型有两个优点［12］:① 与薄板样条等相比，B样条模型是局部可控的，一个节点只会影响邻近4×4×4体素，因此在计算变换函数T(x;d)时效率较高;②B样条基函数是C2连续的，能够计算变换函数T(x;d)的解析梯度，在优化过程中可使用基于梯度的优化方法.传统的B样条模型有可能产生不可逆的变换函数，即当某些节点位移过大时，会导致图像的折叠，从而导致配准失败［11］.为了避免图像折叠，需要对节点位移进行约束.根据三次 B 样条可逆性条件［11］，第i，j，k个节点分别在x，y，z方向上的位移dx，dy，dz应满足条件:

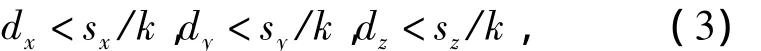
其中k是一常数，在三维空间值为2.479 472 335［11］.在这一约束条件下，图像中体素坐标x的最大位移被限制为(sx/k，sy/k，sz/k)，当且仅当周围4×4 ×4 节点的位移都是(sx/k，sy/k，sz/k)时才能达到.

网格节点的位移是变换函数的参数，因此变换函数的精度取决于网格的间距，小间距的网格能够构建更加精细的变换函数.然而肺部组织在呼吸过程中的位移较大，由于限制了节点位移的大小，必须使用大间距的网格以满足肺部组织的大尺度位移，但又需要小间距的网格以保证变换函数的精度，为了解决这一矛盾，需要使用n层B样条模型框架.n层B样条模型框架依次使用由疏到密的n个网格求得n个变换函数，大间距的网格能够得到大尺度变换函数，满足大尺度形变的要求，小间距的网格能够得到细化变换函数，同时网格节点位移的大小满足上述可逆性约束条件，最终的变换函数是各层求得的变换函数的组合.

文中采用2层B样条模型框架，依次使用两个网格u1和u2，第1层网格u1间距取为60个体素，第2层网格u2间距取为15个体素.整个配准过程从第1层开始，由第1层得到大尺度变换函数Tp，再将Tp作为第2层的初始参数，得到细化变换函数Ti，每一层网格的节点位移都满足可逆性条件，最终的变换函数T是Ti与Tp的组合:

2 基于点集的弹性配准

基于点集的弹性配准目的是生成大尺度变换函数Tp，基于点集的弹性配准分为两步:① 点集提取与CPD点集弹性配准，得到点集坐标位移向量P(Xt，Xf);② 由点集坐标位移向量P(Xt，Xf)得到基于u1的大尺度变换函数Tp.

2.1 点集提取与点集弹性配准

肺表面需要被分割出来以生成表面点集.由于身体部分密度较高，而肺部组织充满空气密度较低，因此CT图像上的身体部分与肺部组织灰度值差异明显，文中采用了一种快速简单的基于阈值和形态学的自动分割方法来分割得到肺的表面区域［9］.

将分割得到的表面区域使用Canny边缘提取算法提取出轮廓面，由于轮廓面上的点数过多，只需要其中的一部分，依据点的坐标分布，均匀地取出轮廓上1/50的点生成肺表面点集.设浮动图像F中取出的肺表面轮廓点数量为N，则浮动图像F的表面点集SF=(xF1，xF2，…，xFi，…，xFN)，其中xFi=(xFix，xFiy，xFiz)，各分量分别表示点xFi在x，y，z方向上的坐标值;设参考图像R中取出的肺表面轮廓点数量为M，则参考图像R中的表面点集为SR=(xR1，xR2，…，xRi，…，xRM)，其中xRi=(xRix，xRiy，xRiz).

肺表面点集反映的是肺的解剖形态，在配准的过程中点集不应改变拓扑结构，一致点漂移算法(CPD)［10］加入了一致性约束，可以保证点集的拓扑结构，非常适用于肺表面点集配准.CPD是一种鲁棒性很强的点集配准算法，能够得到高精度的点集弹性配准结果.它基于混合高斯模型(GMM)，将点集匹配看做概率密度估计问题，给定一对点集a与b，将a看做高斯混合模型的质点，通过最大似然概率完成a与b的匹配，a中的点在配准过程中分别移动到合适的位置以生成配准后的点集c，点集c再与b对齐.

通过CPD算法对肺表面点集SF和SR进行点集弹性配准，将SF作为高斯混合模型的质点，计算SF中各个点的位移，生成配准后的点集ST=(xT1，xT2，…，xTi，…，xTM)，再与SR的对齐.考虑到点集中点的数量较大，使用CPD算法的快速实现［10］:使用低秩矩阵估计与快速高斯变换对算法进行加速.CPD算法中含有3个自由参数:ω，λ和β.其中ω是对噪声数量的假设值，λ和β是平滑性约束参数，文中参数取值为ω=0.7，λ=3和β=4.

2.2 大尺度变换函数Tp

定义点集坐标位移向量P(xT，xF)为

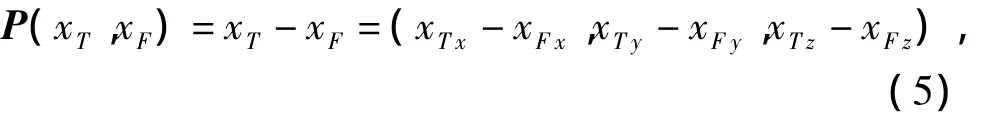
式中:xF=(xFx，xFy，xFz)是点集同SF中的点;xT=(xTx，xTy，xTz)是点集ST中对应于点xF的点.

定义大尺度变换函数Tp为式(1)中的变换函数，大尺度变换函数Tp反映的是包括肺表面组织与内部组织在内的整个肺部组织的位移，点集坐标位移向量P(xT，xF)反映的是肺表面组织的位移，在肺表面组织处由Tp确定的位移向量应该与P(xT，xF)相等，因此使用Tp拟合P(xT，xF):设ΔxF是xF点处由Tp确定的位移向量，则ΔxF与点集坐标位移向量P(xT，xF)相等，即ΔxF到P(xT，xF)的欧几里得距离等于0.

定义点集位移向量P(xT，xF)与ΔxF的欧几里得距离的平方和为

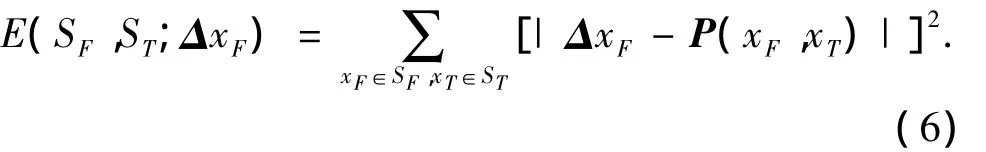
ΔxF是节点位移d的函数，则有

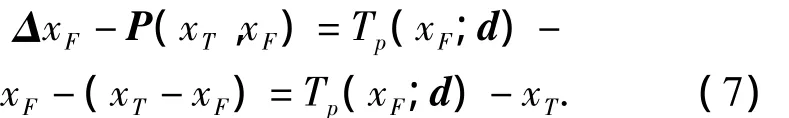
以E(SF，ST;ΔxF)为目标函数，将式(7)代入式(6)可得

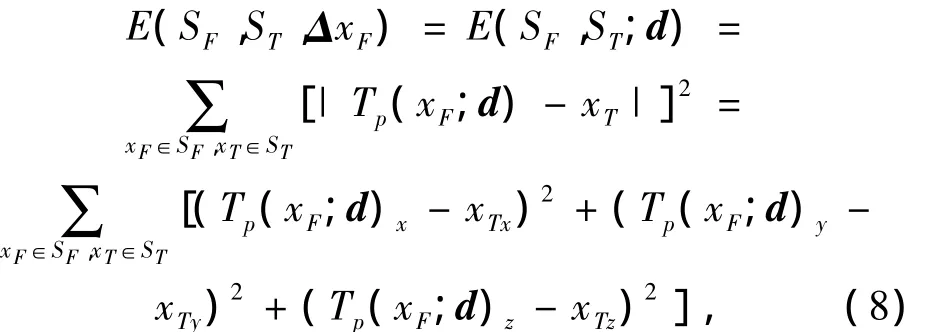
其中下标x，y，z表示变量在x，y，z方向上的分量.式(9)的优化问题是求d以便使目标函数E(Sf，St;d)达到极小值.d为所有节点位移向量，假设有m个节点，则d=(d1，d2，…，di，…，dm)，其中di=(dix，diy，diz)是节点i的位移向量.目标函数E(Sf，St;d)的梯度为

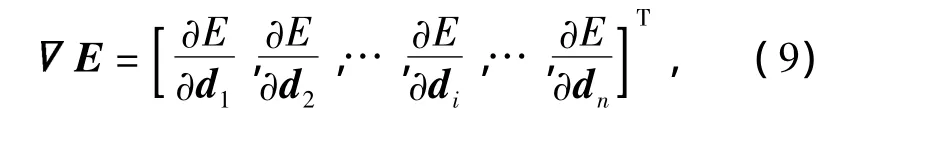
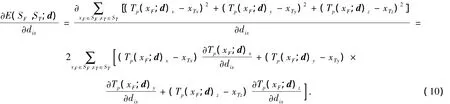
如果Tp的分量的方向与dix的方向不一致，则对应的导数值为0，即为

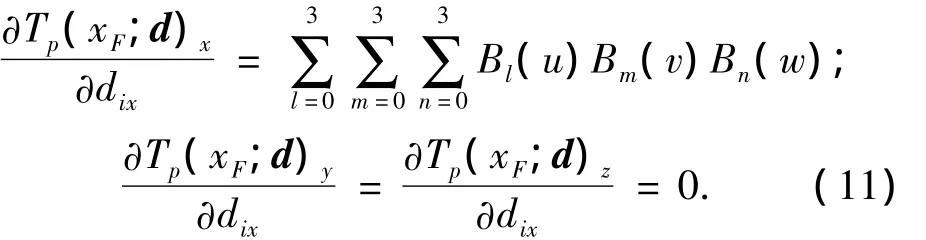
采用有约束的有限容量拟牛顿优化方法LBFGS-B［13］来最小化目标函数E(SF，ST;d).这一优化方法适用于高维度的参数空间，并且能够在优化的过程中对位移向量d的分量di的大小进行约束，我们通过这种方法对节点位移施加前述的可逆性约束条件(2)，以保证配准成功.

3 基于互信息的配准

基于点集的配准得到了大尺度变换函数Tp，这一变换函数反映的是不够精确的大尺度形变，还需对此变换结果进一步细化.很多试验表明，基于灰度的方法对局部形变比较敏感，在图像之间差异比较小的时候能够取得精确的结果［6-7］.由于呼吸运动，肺部组织的膨胀与收缩会导致组织密度的改变，浮动与参考图像中相同的肺部组织对应的灰度值并不一定相等，基于互信息的方法并不直接依赖于灰度值的对应相等关系，因此文中选取基于互信息(mutual information)的Mattes方法［6］对大尺度变换函数Tp进行细化.Mattes方法中互信息目标函数定义为

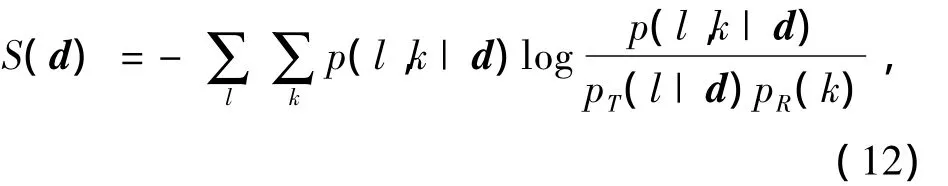
式中:d为节点位移向量;p，pT和pR分别为浮动图像和参考图像的联合概率密度分布函数、浮动图像边缘概率密度分布函数、参考图像边缘概率密度分布函数［6］.Mattes方法使用Parzen窗方法进行连续联合直方图估计以计算互信息目标函数的解析梯度，使用单层B样条模型作为变形模型，使用L-BFGS-B优化方法对互信息目标函数进行优化.

混合配准算法将Tp作为Mattes方法的初始变换函数;设F'是对浮动图像F应用Tp进行变换后生成的图像，将F'作为Mattes方法的浮动图像，将R作为Mattes方法的参考图像;使用2层B样条变形模型中的u2作为Mattes方法的变形模型;使用LBFGS-B优化方法对互信息目标函数进行优化，同时对节点位移施加可逆性约束条件(2)，最终得到细化变换函数Ti(x;d).

4 试验

文中采用4套3D肺部CT图像对该算法进行评估，每一套图像都是肺部运动周期中的最大吸气时刻与最大呼气时刻图像.CT图像的大小为512×512 ×320，空间分辨率是0.97 mm ×0.97 mm ×2.00 mm.试验平台硬件环境是 CPU为 Intel Core i3 2350m@2.3 GHz和RAM为8 GB的计算机.

提取肺表面点集SR与SF，使用CPD对点集SR与SF进行弹性配准.图1显示了肺表面点集SR与SF的提取效果，图2显示了配准前后的点集.

图1 肺表面点集SR与SF

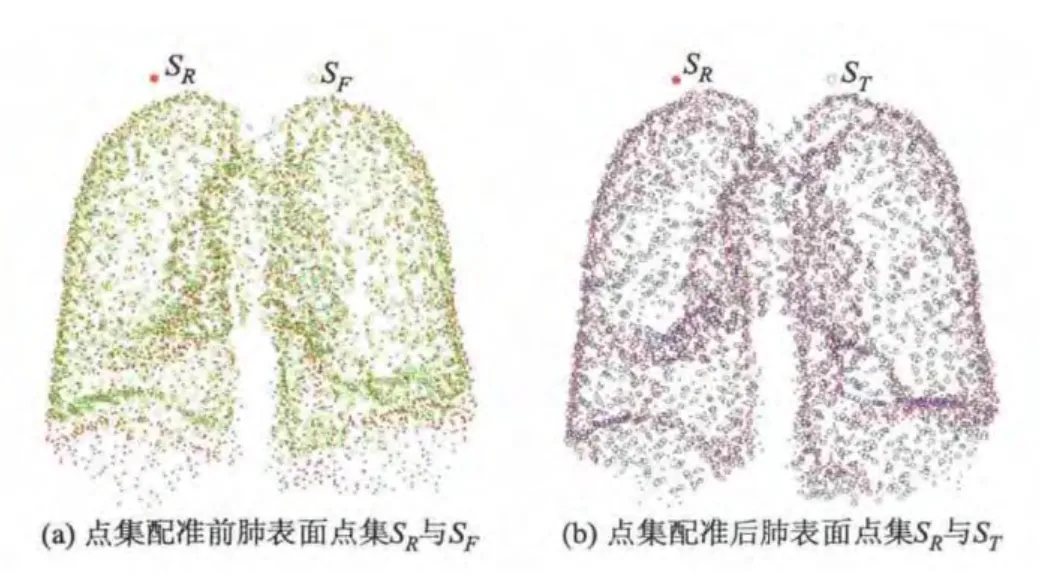
图2 点集弹性配准前后的肺表面点集

算法性能的量化指标由互信息值、标志点距离误差以及计算时间组成.

互信息值反映了一对图像的相似程度，一般互信息值越大则图像越相似.初始的互信息值由浮动图像与参考图像的互信息计算得到，配准后的互信息值由经过变形后的浮动图像与参考图像的互信息计算得到.

标志点距离误差反映了配准算法的精度［14］.使用半自动的标志点标定软件系统(Murphy，2008)［13］对肺部区域内进行标志点标定，使用文献［13］中描述的标定步骤，每一对图像中都标定了250对均匀分布的标志点，每一对标志点表示相同部位在浮动与参考图像上的对应位置.图3以三维视角显示了标志点的分布情况.图4以绿色十字显示标志点标定系统中的标志点位置，由于将所有标志点投影到一层图像上，部分绿色十字显示在该层肺部区域之外.初始的标志点距离误差是浮动和参考图像上对应的每对标志点的欧几里得距离的均值.配准后的标志点距离误差是浮动图像上的标志点坐标与配准结果所预测的标志点坐标的欧几里得距离的均值.

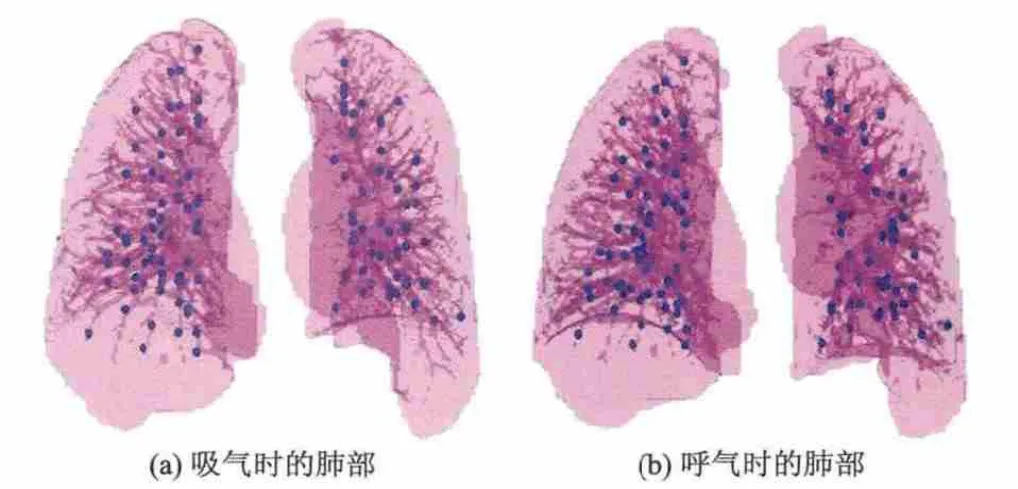
图3 标志点分布示意图(蓝色小球为所选取的标志点)

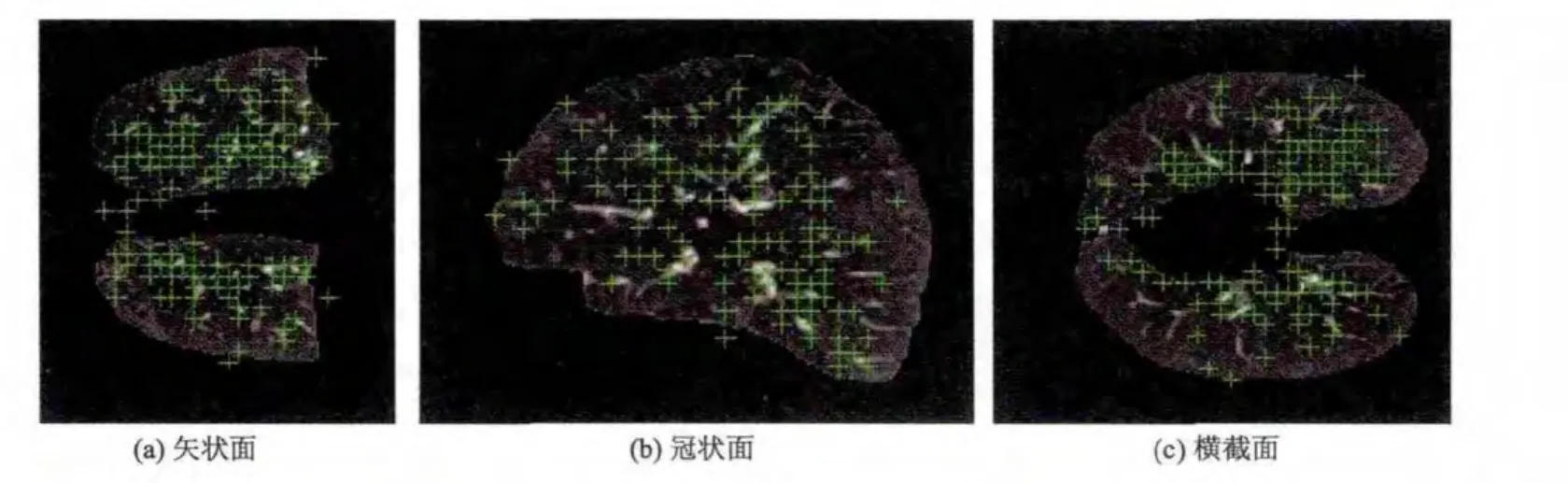
图4 标志点标定系统中标志点的位置(绿色十字形为标志点)

将混合配准算法与仅基于互信息的Mattes方法［6］对相同的图像进行配准得到的结果加以比较，对比结果列于表1中，其中MI表示互信息值，LD表示标志点距离误差，SD表示LD的标准差.Initial是初始值，Mattes代表仅基于互信息的Mattes方法的结果，PR代表混合配准算法中基于点集的配准算法的结果，HR代表混合配准算法的结果.

表1 配准算法的对比结果

由试验结果可以看出，混合配准算法HR具有最小的标志点误差和最大的互信息值，基于点集的配准算法PR的标志点误差最大、互信息值最小，仅基于互信息的Mattes方法的标志点误差与互信息值介于两者之间;仅基于互信息的Mattes方法耗时最多，基于点集的配准算法PR耗时最少，而混合配准算法HR耗时介于两者之间.相对于仅基于互信息的Mattes方法，混合配准算法HR的标志点误差平均减少了5%，互信息值平均提升了1%，耗时平均减少了70%;基于点集的配准算法PR耗时比混合配准算法HR平均减少74%，但混合配准算法HR的标志点误差平均减少了28%，互信息值平均提升了16%.

5 结论

1)相对于仅基于互信息的配准算法，所提方法减少了配准时间，提高了配准精度.

2)点集配准可以生成较精确的大尺度变换函数，为混合配准算法中基于互信息的方法提供了误差较小的初始变换函数，因此经过细化后可以得到误差更小的细化变换函数.

3)混合配准算法能够避免陷入局部极值并拥有更好的鲁棒性，能够获得更小的误差并且加快收敛速度.

4)所提算法对于确定肺部组织的运动轨迹、建立肺部呼吸运动模型、实现计算机辅助术前手术规划与手术导航有很大的帮助.

References)

［1］Boldea V，Sharp G C，Jiang S B，et al.4D-CT lung motion estimation with deformable registration:quantification of motion nonlinearity and hysteresis［J］.Med Phys，2008，35(3):1008-1018.

［2］Dinkel J，Hintze C，Rochet N，et al.Computed tomography of the lungs［J］.Radiologe，2009，49:698-704.

［3］Rueckert D，Aljabar P.Nonrigid registration of medical images:theory，methods，and applications［J］.IEEE Signal Processing Magazine，2010，27(27):113-119.

［4］张俊雄，吴科斌，宋 鹏，等.基于BP神经网络的玉米单倍体种子图像分割［J］.江苏大学学报:自然科学版，2011，32(6):621-625.Zhang Junxiong，Wu Kebin，Song Peng，et al.Image segmentation of maize haploid seeds based on BP neural network［J］.Journal of Jiangsu University:Natural Sci-ence Edition，2011，32(6):621-625.(in Chinese)

［5］Muenzing S E A，van Ginneken B，Murphy K，et al.Supervised quality assessment of medical image registration:application to intra-patient CT lung registration［J］.Medical Image Analysis，2012，16:1521-1531.

［6］Mattes D，Haynor D R，Vesselle H，et al.PET-CT image registration in the chest using free-form deformations［J］.IEEE Trans Med Imaging，2003，22(1):120-128.

［7］Gorbunova V，Durrleman S，Lo P，et al.Lung CT registration combining intensity，curves and surfaces［C］∥Proceedings of ISBI2010 7th IEEE International Symposium on Biomedical Imaging:From Nano to Macro.Rotterdam， Netherlands:IEEE ComputerSociety，2010:340-343.

［8］Yin Y B，Hoffman E A，Ding K，et al.A cubic B-spline-based hybrid registration of lung CT images for a dynamic airway geometric model with large deformation［J］.Physics in Medicine and Biology，2011，56:203-218.

［9］Özkan H，Osman O，Şahin S，et al.Lung segmentation algorithm for CAD system in CTA images［J］.World A-cademy of Science，Engineering and Technology，2011，77:306-309.

［10］Myronenko Andriy，Song Xubo.Point set registration:coherent point drift［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32(12):2262-2275.

［11］Choi Y，Lee S.Injectivity conditions of 2D and 3D uniform cubic B-spline functions［J］.Graphical Models，2000，62:411-427.

［12］Yin Y B，Hoffman E A，Lin C L.Mass preserving nonrigid registration of CT lung images using cubic B-spline［J］.Med Phys，2009，36(9):4213-4222.

［13］Murphy K，van Ginneken B，Pluim J P W，et al.Semiautomatic reference standard construction for quantitative evaluation of lung CT registration［C］∥Proceedings of2008 11th Medical Image Computing and Computer-Assisted Intervention.New York:Springer Verlag，2008:1006-1013.

［14］Murphy K，van Ginneken B，Reinhardt J M，et al.E-valuation of registration methods on thoracic CT:the EMPIRE10 challenge［J］.IEEE Transactions on Medical Imaging，2011，30(11):1901-1920.