基于Harris角点特征的贴片元件视觉定位算法
2014-12-23王祖进黄筱调顾萍萍
王祖进,黄筱调,顾萍萍
(1.南京工业大学机械与动力工程学院,江苏南京210009;2.南京康尼机电股份有限公司,江苏南京210038)
随着贴片元件的微型化以及引脚间距的密集化,芯片贴装领域对贴片机视觉系统的定位精度提出了更高的要求.因此,必须建立速度更快,精度更高的视觉定位算法[1].而贴片机视觉系统定位算法主要包括贴片元件定位和PCB板定位算法2部分:贴片元件定位是对贴片元件中心相对于吸嘴中心的偏移量和贴片元件在拾取过程中的偏转角度进行检测;PCB板定位是通过对母板上的定位标志进行检测,进而得到PCB板坐标系与机器坐标系之间的转换关系.众多学者对贴片机视觉系统的相关算法[2-4]进行了研究,但对偏移量和偏转角度的检测基本都是分开进行的,很少将两者结合起来考虑.为此,文中提出一种基于Harris角点特征的贴片元件定位算法,其中以矩形引脚元件为研究对象,能够同时检测元件的偏移量和偏转角度,且检测精度都达到了亚像素级别.
1 贴片机视觉系统构成
贴片机视觉系统主要结构如图1所示.光学系统由CCD相机和可编程控制的LED光源组成,高速图像采集卡对图像进行采集,然后由PC机上的处理软件对图像进行处理,产生相应的控制信号.

图1 视觉系统结构示意图
2 贴片元件视觉定位算法及其实现
基于Harris角点特征的贴片元件定位算法流程如图2所示.

图2 贴片元件定位算法流程图
2.1 图像预处理
贴片机视觉系统在采集元件图像的过程中,会受到各种噪声和不均匀光照的干扰.通过图像预处理可以消除光照不均匀的影响,滤除噪声,修补图像内部缺陷.首先通过顶帽变换消除光照不均匀的问题,然后利用伽玛变换拉伸元件图像的对比度[5],再运用数学形态学闭运算滤除噪声和修补缺陷[6],最后进行二值化.图像预处理结果如图3所示.

图3 图像预处理结果
2.2 引脚形状判别
元件引脚的形状分为矩形和圆形.不同形状的引脚,相应的定位算法也不同.所以在进行定位之前,需要对贴片元件的引脚形状进行判别.首先用8连通模板对二值图像进行卷积,以标记每个引脚的连通分量,为每个连通区域分配一个唯一的编号,并将输出图像中该连通区内的所有像素赋值为该区域的编号,得到标记图像.以和标记区域具有相同二阶中心矩的椭圆长短轴为特征,来判别元件引脚形状,但实际计算时不需要具体计算出椭圆的长短轴,只要求得标记区域的2个二阶中心矩的比值即可,矩形引脚的比值远大于1,圆形引脚的比值约等于1.
一幅M×N的数字图像f(i,j),其p+q阶几何矩mpq和中心矩μpq为

设X为标记图像的横向坐标矩阵,Y为标记图像的纵向坐标矩阵,大小均为n×1.则标记区域的二阶中心矩的计算过程如下:

表1给出了2个圆形引脚和2个矩形引脚的各阶矩及二阶中心矩的比值.采用上述判别算法对6种类型的贴片元件进行检测,检测结果如表2所示.

表1 部分引脚的矩特征
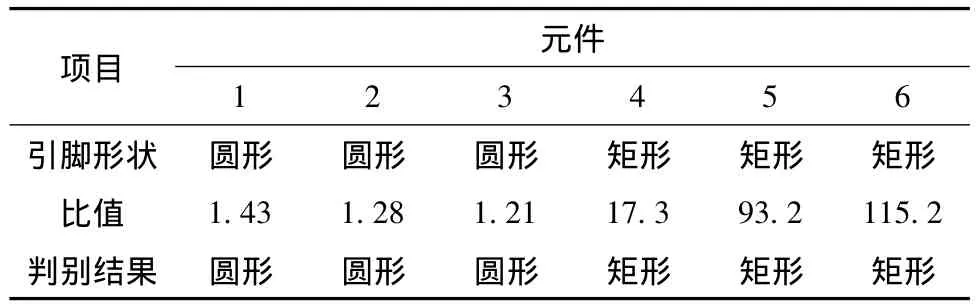
表2 引脚形状检测结果
2.3 偏转角度和偏移量检测
图像的角点是两个边缘的交点,其所在邻域是图像中稳定的、信息丰富的域,具有旋转不变性和平移不变性.Harris算子[7-9]是一种有效的角点特征提取算子,具有计算简单、提取的特征点均匀等优点.所以文中采用Harris角点特征作为贴片元件的定位特征.Harris角点特征提取步骤如下:
1)计算图像I(x,y)在x,y方向上的梯度Ix,Iy:

式中:
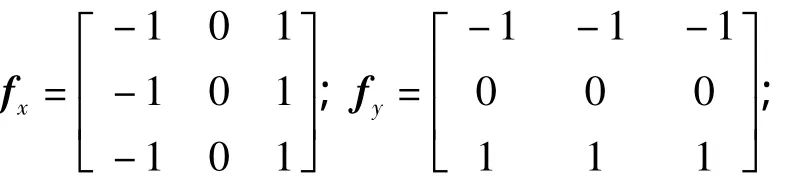
⊗为卷积运算.
2)计算图像x,y方向梯度的乘积:

3)使用高斯函数对梯度乘积进行高斯加权:

式中w为9×9的高斯窗函数.
4)计算自相关矩阵M的行列式detM和直迹traceM:
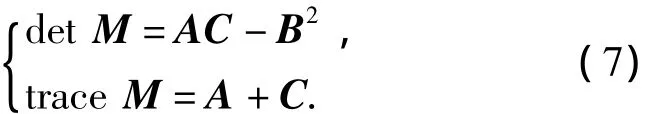
5)计算每个角点的响应值R,并对小于阀值t的R置0:

式中α为经验常数,取值0.04.
6)在3×3的邻域内进行非极大值抑制,余下的局部极大值点即为图像的角点.
角点特征的提取结果如图4所示.

图4 角点特征提取结果
在xy坐标系中标注出每个角点,然后找出具有x轴坐标最大、最小值以及y轴坐标最大、最小值的4个基准角点,最后通过计算其他角点与4个基准角点的距离来判断剩余角点与哪个基准角点属于同一类.通过最小二乘法对4类角点进行直线拟合,并将拟合得到的直线平移0.75l(l为贴片元件的引脚长度),去除已分类的角点,剔除虚假角点,对余下的角点再次进行分类和最小二乘拟合,最后取8条直线斜率的平均值作为偏转角度θ的检测结果.其中虚假角点的判别方法是将余下角点分别带入平移后的4条直线的直线方程,得到4个值y1,y2,y3,y4,若4个值中正数的个数为2,则此点为4条直线所构成的封闭区间内的点,否则为虚假点.处理结果如图5所示.
常用的图像配准方法[10-11]包括基于灰度的配准方法和基于特征的配准方法.基于灰度的图像配准方法对图像的灰度变化比较敏感,计算的复杂度高,对目标的旋转、形变以及遮挡比较敏感;基于特征的图像配准方法[12-13]可以克服基于灰度的图像配准方法的缺点,在图像配准领域得到了广泛的应用.图像的特征点比图像的像素点要少很多,大大减少了匹配过程的计算量;特征点的匹配量值对位置的变化比较敏感,匹配的精确程度高;特征点的提取过程可以减少噪声的影响,对灰度的变化、图像形变以及遮挡等都有较好的适应能力.所以文中采用基于Harris角点的图像配准方法对贴片元件的偏移量进行检测.
首先采用双三次插值法对原灰度图像进行旋转和放大,旋转角度为-θ,放大倍数为2.因为特征点的坐标都为整数,使得最后检测出的偏移量只能为整数个像素,无法检测出小于1.0个像素的偏移量.而对图像进行放大处理,可使误差由原来的1.0个像素减小为0.5个像素,从而实现偏移量的亚像素检测.最后提取几何变换后的图像与未发生偏移的标准图像的Harris角点特征,取角点附近的8.0个像素值作为匹配特征点向量,并进行匹配,去除匹配错误点,得到最佳匹配点对,匹配点对间的坐标差值即为贴片元件的偏移量.最终的匹配结果如图6所示.
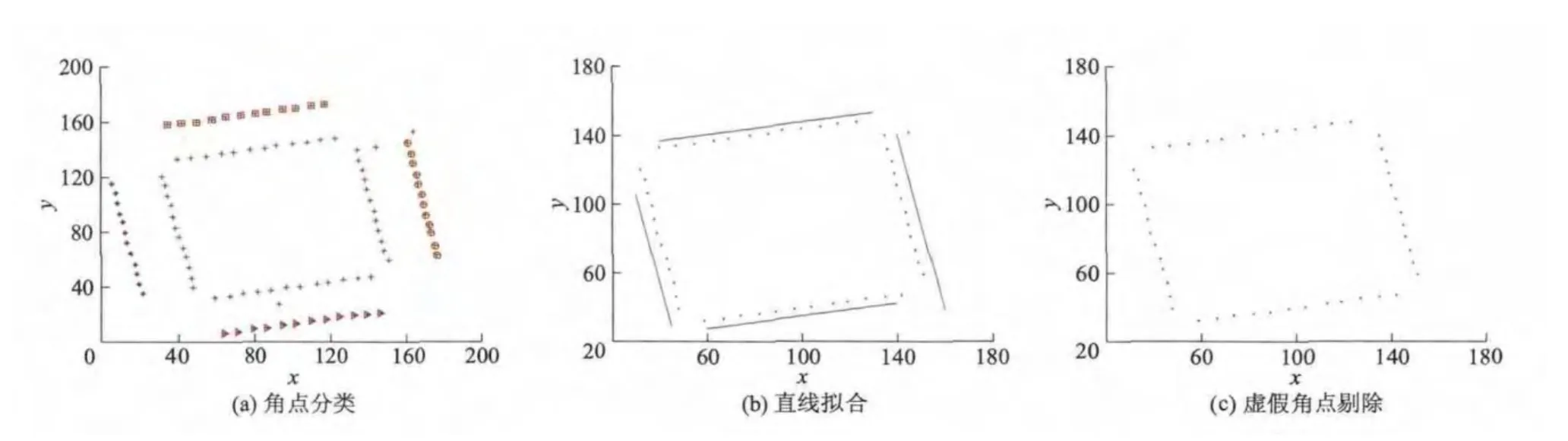
图5 处理结果

图6 图像配准结果
3 试验及结果分析
试验中以TQFP48-P-0707-0.5-K(如图3a所示)型贴片元件为被测对象.偏转角度的检测结果如表3所示,偏移量的检测结果如表4所示.由表3,4可以看出,文中算法对偏转角度的检测误差小于0.1°,以像素来度量则小于 0.5 个像素,对偏移量的检测误差小于25 μm,以像素来度量则小于0.5个像素,两者的检测精度都到达了亚像素级别.

表3 偏转角度检测结果

表4 偏移量检测结果
4 结论
在分析现有贴片元件定位方法的基础上,提出了一种基于Harris角点特征的贴片元件定位方法,以矩形引脚元件为研究对象.首先采用顶帽变换、伽玛变换以及数学形态学闭运算对元件图像进行预处理;然后标记元件引脚的连通区域,计算二阶中心矩,以判别元件的引脚形状;再通过Harris角点特征提取、分类和直线拟合等得到元件的偏转角度;最后对元件图像进行旋转和放大处理,并进行基于Harris角点特征的图像配准,得到最佳匹配点对,匹配点对间的坐标差值即为贴片元件的偏移量.检测结果表明,文中算法能够同时检测贴片元件的偏移量和偏转角度,偏移量误差小于25 μm,偏转角度误差小于0.1°,检测误差均小于 0.5 个像素,达到了亚像素精度.
References)
[1]孙 力,蔡健荣,李永平,等.基于TOF成像技术的柑橘实时识别与定位[J].江苏大学学报:自然科学版,2013,34(3):293-297.Sun Li,Cai Jianrong,Li Yongping,et al.Real-time citrus recognition and location based on TOF imaging technology[J].Journal of Jiangsu University:Natural Science Edition,2013,34(3):293-297.(in Chinese)
[2]Lin C S,Lue L W.An image system for fast positioning and accuracy inspection of ball grid array boards[J].Microelectronics Reliability,2001,41(1):119-128.
[3]Yeh C H,Shen T C,Wu F C.A case study:passive component inspection using a 1D wavelet transform[J].International Journal of Advanced Manufacturing Technology,2003,22(11/12):899-910.
[4]解杨敏,刘 强.高精度自动贴片机视觉系统定位算法研究[J].光学技术,2008,34(3):449-454.Xie Yangmin,Liu Qiang.Research on locating algorithm of vision alignment system in automatic high precision chip mounter[J].Optical Technique,2008,34(3):449-454.(in Chinese)
[5]王祖进,黄筱调.基于形态学的元件图像边缘检测算法[J].南京工业大学学报:自然科学版,2013,35(2):115-118.Wang Zujin,Huang Xiaodiao.Chip image edge detection algorithm based on morphology[J].Journal of Nanjing University of Technology:Natural Science Edition,2013,35(2):115-118.(in Chinese)
[6]关柏青,于新瑞,王石刚.基于链码分析及矩特征的元件类型检测方法[J].上海交通大学学报,2005,39(6):969-974.Guan Baiqing,Yu Xinrui,Wang Shigang.An inspection method of component type based on moment features and chain code[J].Journal of Shanghai Jiaotong University,2005,39(6):969-974.(in Chinese)
[7]Lin H,Du P,Zhao W,et al.Image registration based on corner detection and affine transformation[C]∥2010 3rd International Congress on Image and Signal Processing,2010:2184-2188.
[8]Bellavia F,Tegolo D,Valenti C.Improving Harris corner selection strategy[J].IET Computer Vision,2011,5(2):87-96.
[9]Chen J,Zou L,Zhang J,et al.The comparison and application of corner detection algorithms[J].Journal of Multimedia,2009,4(6):435-441.
[10]Manuel G S,Thurman S T,Fienup J R.Efficient subpixel image registration algorithms[J].Optics Letters,2008,33(2):156-158.
[11]Wyawahare M V,Patil P M,Abhyankar H K.Image registration techniques:an overview [J].Image Processing and Pattern Recognition,2009,2(3):11-26.
[12]文贡坚,吕金建,王继阳.基于特征的高精度自动图像配准方法[J].软件学报,2008,19(9):2293-2301.Wen Gongjian,Lü Jinjian,Wang Jiyang.An automated method for feature-based image registration with high-accuracy[J].Journal of Software,2008,19(9):2293-2301.(in Chinese)
[13]Liao S,Chung A C S.Feature based nonrigid brain MR image registration with symmetric alpha stable filters[J].IEEE Transactions on Medical Imaging,2010,29(1):106-119.
