支架导学，抵达思维深处

黄春芬

苏教版《数学》第九册《解决问题的策略——列举法》一课，旨在用列举的方法去解决实际问题。所谓列举，即把事情发生的各种可能逐个罗列，并用某种形式进行整理，从而得到问题的答案。生活中有许多实际问题，列式计算往往比较困难。如果联系生活经验，用一一列举的方法能比较容易地得到解决。因此，一一列举是解决问题的常用策略之一。教学生认识列举法，且在一一列举的时候要学会有序地思考，做到不重复、不遗漏，这对小学生来说，有一定的挑战。数学是理性思维的学科，小学生却正处于感性思维的年龄。如何针对小学生的特点而又逐步发展学生的数学理性思维呢？依维果斯基的最近发展区理论看来，这就需要在学生思维发展起点与目标之间搭建支架，让学生经过浅近目标的实现，而逐步抵及思维发展的彼岸。本节课教学通过设计一系列的支架，在学生心理情绪纠结处设计情境，纾解引导;在知识技能掌握未竟处提供实践平台，加强巩固等等，步步引导，及时帮扶，将学生引入思维深处，取得良好的教学效果。

一、创设问题支架，快乐感知列举法

【课例】师：以前我们曾学过一些解决问题的策略，知道在生活中遇到难题时，要学会思考。今天我们来学习一种新的解题策略。

1. 出示：在练习本上画出周长是6厘米的长方形（长和宽都是整数），并标出长和宽。

（1）投影展示学生的画法。

（2）提问：你在画的时候是怎样想的？

教师小结：长+宽=周长的一半（板书）。

2. 出示：周长是10厘米的长方形（长和宽都是整数），有几种不同的围法？

要求：可以直接写出长和宽各是多少，也可以画图表示。

（1）投影展示学生列出的情况以及两种画法。

（2）提问：你是怎样想到有两种围法的？

教师小结：在周长不变的条件下，长方形的形状可能会出现不同的情况，我们可以根据长、宽的和是周长的一半进行设计，这样比较方便。

提到“策略”、“列举法”这类概念，学生容易产生心理抵触。但这个概念又确实需要跟小学生谈清楚，怎么办？迂回了一下，一开始用一个浅近的实践性的题目让学生参与，很快地调动起学生参与的热情，果然取得较好的效果。这样一个实践性的题目就是一个实践性的问题支架，通过这个实践过程，让学生走近列举法，初步感知列举法。策略因问题解决的需要而由学生自然生成，当他们以后再面临类似问题时，策略的应用便会是自发的、能动的，是有意识的积极行为。

曾经遵循教材，安排学生摆小棒列举，然在实际教学中不太容易操作，要求多，过程繁杂，现场不太容易控制，会占用较多的教学时间。本环节安排学生“画出周长是6厘米的长方形和设计周长是10厘米的长方形”，通过画图，每位学生都能参与，且操作起来方便，很自然地引出“长方形设计的关键在于长+宽=周长的一半”。此外，因为数字较小，学生容易想到列举尝试来解决问题，这对于后面揭示课题，提出这是新的解决问题的策略，能有效地成全学生获得成功的体验，很容易与新学的“列举法”建立起内在的亲近感。

二、设置情境支架，组织自主探究

【课例】师：同学们，听说大家都乐于助人。现在就有一个情况，小华跟着爸爸妈妈一起去农场参观，他看到王大叔正在为围羊圈的事犯愁呢？原来邻居王大叔遇到了一个数学难题，请同学们帮帮王大叔好吗？（课件出示例1：王大叔用18根1米长的栅栏围成一个长方形羊圈，有多少种不同的围法？ ）

要求：动脑筋想一想，然后把可能出现的情况按一定的顺序写在你的练习本上。

（1）学生独立思考后，完成在练习本上。

2）同桌交流各自的策略和解题答案。

（3）师展示学生列举的四种围法。（注意收集有序和无序两种情况）

（4）讨论：你认为哪一位同学在列举的时候做得比较好，为什么？

教师小结：根据长与宽的和是周长的一半，我们列举出四种不同的围法。如果列举的时候按照一定的顺序进行，就会避免重复和遗漏。“列举”就是我们今天要研究的解决问题的新策略。（板书：列举）

例1体现了按顺序列举的解题策略，而学生在初次使用列举法解题时，常常会出现无序列举的情况。本环节通过组织学生对比讨论。使学生认识到按一定的顺序列举会很好地避免重复和遗漏。以实践加讨论交流，加深有序列举的鲜明要求。这样的设计实际上是找到了学生认知中的难点，通过交流这个支架加以强调，边学边思，有效提升学习的效果。

【课例】师： 某某同学列举得很有条理，有条理既能帮助我们理清思路，还能确保我们避免遗漏，因此是非常必要的。其实，某某同学的做法完全可以借助表格来列举。

（5）介绍用列表的形式进行列举。教师课件显示正确答案，反馈矫正。

答：一共有4种不同的围法。

（6）提问：观察表格，王大叔会选哪一种围法修建羊圈呢？为什么？

（7）学生同桌讨论。

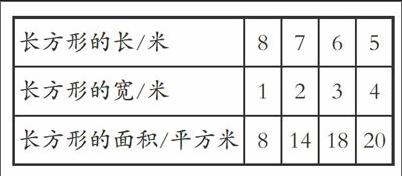
（8）提问：在周长不变的条件下，长方形的长、宽和面积有什么关系？

教师小结：在长方形周长不变的条件下，长和宽越接近，面积越大;长和宽相差越大，面积越小。此外， 引导学生体会画表列举法的优越性。（板书：画表列举可以做到有序、不重复、不遗漏。）

相对于上面的准备题，例1的难度系数显然有所提高。为了让学生不至于产生畏难心理，我有意设置一个情境，帮王大叔解决生活中的困难，由此让学生小组合作交流，分工操作完成。这样一个情境支架的设计，着眼于学生的心理，营造出乐于助人的氛围，也增强了数学学习与生活之间的联系，可谓一举多得。事实上各小组在组长的组织下，有条不紊地进行着合作探究，成功地解决了问题。在教学中，我还有意渗透解题的方法，通过为王大叔选地，很自然地引出有关“面积”的话题，而对“在周长不变的条件下，长方形的长、宽和面积有什么关系”的思考，则有机地渗透了“通过列举找规律”的解题意识。这从内容与形式上都在积极地指向教学目标。endprint

三、提供实践平台，验证巩固所学

【课例】师：有一个音乐钟，每隔一段相等的时间就会发出铃声。已经知道上午9∶00、9∶40、10∶20和11∶00发出铃声，那么下面哪些时刻也会发出铃声？

13∶00 14∶40 15∶40 16∶00

1. 学生独立审题。

2. 提问：11∶00后发出铃声的时刻是多少？为什么？要想判断哪些时刻也会发出铃声，你准备怎么办？

3. 学生同桌讨论后，完成在练习本上。

4. 集体评议。

学会用表格列举，理清解题思路，这样的思考方法不能浅尝辄止，需要及时的练习巩固。教师将练习中的一个很生活化的题目及时抽调过来，让同学们来自主解决。学生纷纷行动，并积极汇报。师生在评点发言同学的思路的同时，实际上是在对照梳理自己的解题思路，反思自己思考中的成败与问题。适当运用所学解决现实问题，及时巩固所学，显然是必要的。其实这也是从认知到实践再到认知的螺旋上升的学习过程。

四、出示问题支架，启迪思维突围

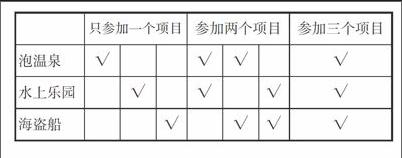
【课例】南京汤山温泉推出泡温泉、水上乐园、海盗船三个娱乐活动项目供游客玩耍，游客最少参加1个项目，最多参加3个项目。有多少种不同的选择？

1. 组织学生讨论交流，教师巡视并作适当的辅导。设置几个问题支架——

（1）“最少参加1个项目，最多参加3个项目。”表示什么意思？

（2）如果只参加1个项目有多少种不同的选择？参加2个项目呢？参加3个项目呢？所以一共有多少种不同的选择呢？

（3）完成表格。

2. 学生汇报探讨结果。

（1）引导学生回答探讨的问题。

（2）投影展示学生所做的表格。

3. 课件出示正确答案，反馈矫正。

答：一共有7种不同的选择。

4. 质疑1：表格所显示的是7种还是12种不同的选择呢？（有部分学生把表格中所有的“∨”数出是12个，误认为12种。）

质疑2：如果分别用A、B、C代表泡温泉、水上乐园、海盗船三个娱乐活动项目，你能用字母表示一一列举出所有不同的选择吗？

5. 解疑。

解决问题的策略设置了大量的实践性问题，编者意图显然是通过大量的实践操作，以加强列举策略的实践，以形成习惯性的意识。对此，我有意联系家乡的美好风光与游乐项目编写实际问题，既对学生进行热爱家乡热爱生活的教育渗透，又是充分联系学生的生活经验，运用所学知识来解决现实问题。关于游乐项目的问题解决，关键不在于表格的列举，而在于对这一生活问题的认知和分析。因此有意设置辅助问题支架，为学生指向引路，充分发挥问题支架的引路帮扶作用，使其逐步进入思考分析的状态。他们一旦明晰思路，问题将引刃而解。

五、呈现思维流程支架，拓展思维宽度广度

【课例】订阅下面的杂志：《科学世界》《七彩文学》《数学乐园》。最少订阅1本，最多订阅3本。有多少种不同的订阅方法？

1. 提问：如果你是读者，你会订阅哪些杂志？

2. 提问：同学们有的只订阅1本，有的订阅2本，还有的3本都订阅。究竟有多少种不同的订阅情况？你怎样解决这个问题？

3. 全班展开讨论，讨论中肯定学生用简洁的方式分三种情况来列举。

4. 学生在练习本上自主选用不同的形式列举。

5. 集体评议，投影展示学生的各种解题策略。

6. 指名学生到讲台上，在实物投影仪下尝试用列表法列举。

教师小结：列举时无论使用什么样的形式，要想获得全部答案，就要全面地考虑问题，有条理地进行列举。

学习列举法不是目的，只是手段，解决问题才是目的。因此，在学生基本掌握列举法之后，更重要的是在实际情境中能灵活运用。在新课结束之际布置这样一个问题，希望学生在没有教师指引的情况下来独立解决问题，这显然比课堂上有老师同学商讨下解决问题增加了一点难度。对此，教师并没有甩手，而是针对学生对现实问题现象中难以寻找到切入口的问题，出示一个思考的流程，引导学生理解题意，形成思路后放手练习，这样会很好地提高思维的有效性。事实证明，这样的辅助和引导是非常必要的。大多数学生能运用所学，有效地解决了这个问题。

（作者单位：南京师范大学附中江宁分校）

本栏责任编辑 李 淳endprint