塔康高精度测角及抗野值研究

彭大国，李治安，李晓明，裴文林

(空军工程大学信息与导航学院，西安710077)

0 引言

塔康(tactical air navigation system，TACAN)是近程无线电导航系统，可以为飞行目标提供方位和距离信息［1］。塔康测角是方位测量的中心环节，受外界噪声、多径干扰等因素影响，测试数据会不可避免的出现野值。本文通过分析新息的特性，给出野值(outlier)的判定准则，重构状态估计，建立自适应抗野值Kalman滤波模型，并与最小二乘曲线拟合相结合，实现对塔康测角的高精度解算。该测角方法与文献［2］中的方法都具有很高的解算精度，不同的是本文通过最小二乘曲线拟合解算方位，经抗野值Kalman滤波器抑制野值，二者相比较，本文具有抑制野值和抗干扰能力强的优势。

对于抗野值Kalman滤波器的研究，文献［3］提出利用残差序列统计特性进行决策来判断并剔除野值，该方法直接将野值剔除，没有充分利用野值的有用信息。文献［4］提出了利用新息正交性并引入活化函数修正新息的抗野值方法，该方法野值的判定准则未进行定量分析，门限受扰动量ε的影响较大。文献［5］提出了基于模糊控制器的Kalman滤波来抑制野值影响，但抑制效果对模糊控制器模糊规则的依赖性强。本文建立的抗野值Kalman滤波模型，不仅具体推导出判决门限的表达式，并引入压缩影响函数对状态增益进行修正，根据野值偏离程度实现不同程度的抑制，充分利用了野值的有用信息，抗野值性能好，同时不需要观测值的先验统计特性，运算量小，易于工程实现。

1 最小二乘曲线拟合

塔康方位包络信号的表达式为

(1)式中:U为载波信号幅值;f1=15 Hz，f2=135 Hz;m1，m2分别为15 Hz和135 Hz的正弦信号调制度;φ1，φ2分别为15 Hz和135 Hz信号初相。

对包络信号进行采样得到N个数据点{(xk，yk)}(k=1，2，…，N)，由于信号表达式形式是已知的，定义5个相互独立的函数{fj(x)}(k=1，2，…，5)就可以拟合出信号，分别为 1，sin(30πt)，cos(30πt)，sin(270πt)，cos(270πt)，用 fj(x)的线性组合来拟合 f(x)［6－7］，其中，f1(x)=1 用来拟合信号中的直流分量，f(x)的表达式为

(2)式中，cj(j=1，2，…，5)为与函数 fj(x)对应的拟合系数。当拟合误差平方和最小时所得曲线为拟合曲线，拟合误差平方和为

为使 E(c1，c2，c3，c4，c5)的值最小，E 关于 cj的所有偏导都为0，即∂E/∂cj=0。求解得到(4)式

交换求和次序，得到一个关于{cj}的线性方程组:

采用矩阵简化方程为

(6)式中:C=［ c1，c2，c3，c4，c5］T，Y=［y1，y2，y3，…，yN］T

求解(6)式得到:

持续接收塔康包络信号，每接收到N个数据进行一次拟合，求解得到一组系数 c1，c2，c3，c4，c5。c1表示直流分量的系数与测角无关，因此，我们取C=［c2，c3，c4，c5］T。

多次拟合后得到系数矩阵［C1，C2，C3，C4，…］，Ci(i=1，2，…)为第i次拟合得到的C。系数矩阵中可能含有野值，因而，将矩阵送入抗野值Kalman滤波器中进行抗野值处理。

2 抗野值kalman滤波器

野值点为严重偏离大部分数据所呈现变化趋势的一小部分数据点［8－9］。含有野值的数据输入 Kalman滤波器会使状态修正出现偏差，造成滤波结果偏离真实状态，产生不利影响，因此，下面提出一种具有抗野值特性的Kalman滤波算法。

2.1 模型的建立

建立模型的量测方程为z(k)=Hx(k)+ξ(k)，其中，z(k)为最小二乘拟合出的系数矩阵，作为模型中的量测值;x(k)为状态变量;H为量测4阶单位矩阵，ξ(k)为量测噪声，服从N(0，R)的高斯分布，R为协方差矩阵。建立模型的状态方程为x(k)=Cx(k－1)+Γu(k)，其中，C为4阶单位状态转移矩阵;u(k)为4维的系统噪声，服从N(0，Q)的高斯白噪声，Q为协方差矩阵;Γ为噪声驱动。

Kalman滤波模型［10］的状态估计为

在(10)式中引入压缩影响函数对状态增益进行修正，因而，首先要建立适当的判决门限，判断输入数据是否为野值，其次，要选取合适的压缩影响函数，能根据偏离程度的不同实现不同程度的压缩。

2.2 判决门限的确定

门限r的作用是判断量测数据是否为野值。由文献［11］可知，新息可以反映出量测信号的统计特性，利用其特性，详细推导出判决门限的表达式。

新息 w(k)=［w1(k)，w2(k)，w3(k)，w4(k)］T服从4维的正态分布，新息的协方差 G(k)=E［w(k)w(k)T］，对 w(k)和wT(k)进行归一化，得到归一化新息及其转置:

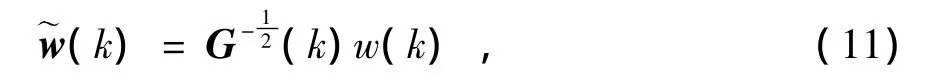
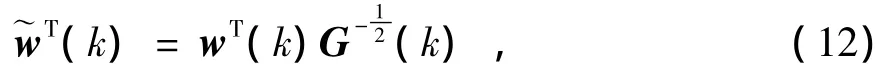
归一化新息与其转置相乘得

对(13)式求迹得:

新息为

(15)式中:x(k)为二乘法输出的系数矩阵;v(k)为量测噪声。

由文献［11］可得新息的协方差为

取判决门限r为

(17)式中，

由(12)式、(13)式和(18)式可得:

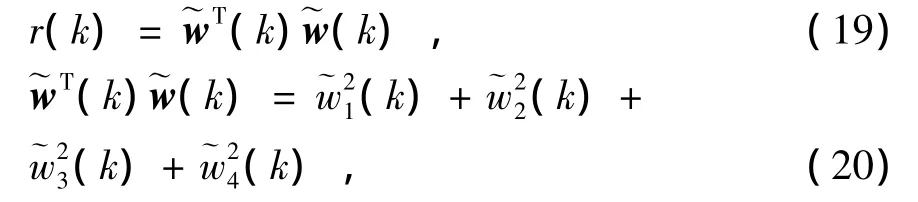
可以推导出:

因此，我们可以建立如下的判决门限:

r(k)≤χ2α(4)，测量值不是野值;r(k)≥χ2α(4)，测量值是野值。

χ2α(4)分布置信度为(1 －α)·100%的分位点，本文中 α 取 0.025，查表得 χ2α(4)=11.1433。

2.3 压缩影响函数的确定

在(9)式中引入压缩影响函数Φ(k)对滤波增益K(k)进行修正［12］。本文采用压缩影响函数不是简单的对野值进行剔除，而是充分利用野值的有用信息，根据野值偏离程度实现不同程度的压缩，Φ(k)的表达式为

记Δw(k)为经压缩影响函数Φ(k)修正后的新息，则Δw(k)的表达式为

下面证明引入的压缩影响函数Φ(k)未改变Kalman滤波器的特性。首先证明修正后的新息与原新息的统计特性是一样的。

证:

1)当r(k)≤χ2α(4)时，此时测量值不是野值，Φ(k)=1，修正新息等于原新息，统计特性一致;

2)当r(k)＞χ2α(4)时，此时测量值是野值，则:

从上面的证明可知，当野值存在时，修正后的新息与原新息的统计特性是一致的。下面证明改进后的Kalman滤波器的状态估计误差方差矩阵P(k|k)是最小的。

证:

在改进后的Kalman滤波器中，状态估计误差方差矩阵P(k|k)与经典Kalman中的P(k|k)是完全一致的，也就是说改进后的Kalman滤波器的状态估计误差方差矩阵P(k|k)是最小的。

通过上面的2个证明可以知道，引入的压缩影响函数Φ(k)没有改变新息的统计特性，且误差方差矩阵是最小的，故选取的压缩影响函数Φ(k)符合要求。

3 方位确定

由最小二乘法拟合出的系数在经过改进的Kalman滤波器滤波之后输出，其15 Hz正弦初相θ［13］1的确定由表1给出，表1中符号“+”表示该值为正，“－”表示该值为负。

表1 正弦初相的确定Tab.1 Initial phase of the sinusoidal signal

同样根据c4和c5可以得到135 Hz正弦信号初相 θ2。

由 θ1，θ2求方位角为

4 仿真实现与结果分析

4.1 仿真条件

基于CV模型，假设塔康包络信号为

在信号中叠加2%的高斯白噪声和幅度为信号幅度10%的野值，每采集200组数据进行一次拟合，将拟合出的系数分3路分别送入本文采用的Kalman滤波器、文献［8］中采用的Kalman滤波器和普通Kalman滤波器中，输出的系数根据表1和(24)式解算出方位值。

4.2 仿真结果及分析

仿真结果如图1和图2所示。

图1 含野值情况下方位解算值Fig.1 Azimuth values with outlier

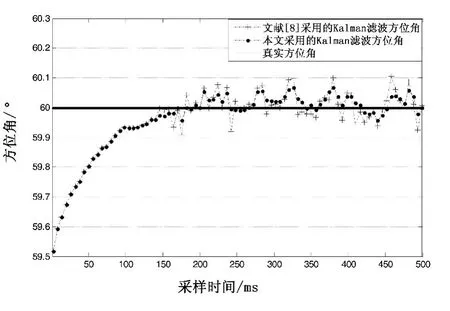
图2 本文与文献［8］的Kalman滤波器解算方位值比较Fig.2 Azimuth values of this paper compared with literature［8］

由图1可知，在野值出现时，本文提出的抗野值Kalman滤波器对野值的抑制作用要明显优于经典Kalman滤波器;由图2可知，本文提出抗野值Kalman滤波器对野值的抑制程度要略优于文献［8］中的Kalman滤波器，但文献［8］中判决门限的确定需要对大量数据进行统计学分析，运算量大大高于本文算法。仿真结果表明，该算法实现了对塔康测角的高精度解算，并能有效抑制野值，具有很高的精度和抗干扰能力。

5 结束语

本文提出的抗野值塔康测角方法能实现塔康方位的高精度解算，设计了一种抗野值Kalman滤波器，引入压缩影响函数修正状态增益，推导出判决门限的表达式，并进行了仿真分析。该方法能很好地抑制野值干扰，实现塔康高精度测角，且算法简单，运算量小，抗干扰能力强，易于工程实现。

［1］张忠兴，李晓明，张景伟.无线电导航理论与系统［M］.西安:陕西科学技术出版社，1998.ZHANG Zhongxing，LI Xiaoming，ZHANG Jingwei.The Theory and System of Radio Navigation［M］.Xi＇an:Shaanxi Science and Technology Press，1998.

［2］张国祥，郭英，霍文俊，等.基于Kalman滤波的塔康方位精确解算方法［J］.空军工程大学学报:自然科学版，2013(2):76－80.ZHANG Guoxiang，GUO Ying，HUO Wenjun，et al.Accurate calculating method of TACAN bearing signal based on Kalman filtering［J］.Journal of Air Force Engineering University:Natural Science Edition，2013(2):76－80.

［3］刘承香，孙枫.野值存在情况下组合导航系统的容错技术研究［J］.中国惯性技术学报，2002，10(6):12－17.LIU Chengxiang，SUN Feng.Fault tolerant on integrated Navigation system when existing outliers［J］.Journal of Chinese Inertial Technology，2002，10(6):12－17.

［4］柳海峰，姚郁，卢迪，等.Kalman滤波新息正交性抗野值法研究［J］.电机与控制学报，2003，7(1):40－42.LIU Haifeng，YAO Yu，LU Di，et al.Study for outliers based on Kalman filtering［J］.Electric Machines and Control，2003，7(1):40－42.

［5］郑梅，程向红，万德钧.模糊卡尔曼滤波器在初始对准抗野值修正中应用［J］.中国惯性技术学报，2006，13(6):18－20.ZHENG Mei，CHENG Xianghong，WAN Dejun.Application of fuzzy Kalman Filter in Anti－coarse Value Correction of Initial Alignment System［J］.Journal of Chinese Inertial Technology，2006，13(6):18－20.

［6］张浩杰，李晓明，裴文林.基于中频数字化技术的塔康测角方法研究［J］.现代防御技术，2012，40(3):67－71.ZHANG Haojie，LI Xiaoming，PEI Wenlin.Angle Measuring of TACAN Based on IF Digital Technique［J］.Modern Defence Technology，2012，40(3):67－71.

［7］王伟斌，邱长泉.基于最小二乘曲线拟合的信号调理电路误差补偿方法［J］.计算机测量与控制，2009(11):2286－2288.WANG Weibin，QIU Changquan.Compensating error of signal conditioning circuit based on least square curve fitting［J］.Computer Measurement and Control，2009(11):2286－2288.

［8］卢迪，姚郁，贺风华.一种抗野值的 Kalman滤波器［J］. 系统仿真学报，2004，16(5):1027－1029.LU Di，YAO Yu，HE Fenghua.Kalman filter restraining outliers［J］.Journal of System Simulation，2004，16(5):1027－1029.

［9］GADZHIEV C M.Testing the Covariance Matrix of a Renovating Sequence under Operating Control of the Kalman Filter［J］.Automation and remote control，1996，57(7):1046－1052.

［10］付梦印，邓志红，闫莉萍.Kalman滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2010.FU Mengyin，DENG Zhihong，YAN Liping.The theory of Kalman filtering and its application in navigation system［M］.Beijing:Science Press，2010.

［11］李广军，李忠，崔继仁.新型抗野值的Kalman滤波器研究［J］.计算机应用与软件，2013，30(1):136－138.LI Guangjun，LI Zhong，CUI Jiren.Research on new Kalman Filter Restraining outliers［J］.Computer Applications and Software，2013，30(1):136－138.

［12］高宁，周跃庆，杨晔，等.抗野值自适应卡尔曼滤波方法的研究［J］.中国惯性技术学报，2003，11(3):25－28.GAO Ling，ZHOU Yueqing，YANG Ye，et al.Adaptive Kalman filter algorithm with fault－tolerant improvement［J］.Journal of Chinese Inertial Technology，2003，11(3):25－28.

［13］王玉林，李艳斌.基于线性组合的塔康方位信号处理［J］. 无线电工程，2006，36(11):38－40.WANG Yulin，LI Yanbin.TACAN bearing signal processing based on the linear combination［J］.Radio Engineering，2006，36(11):38－40.